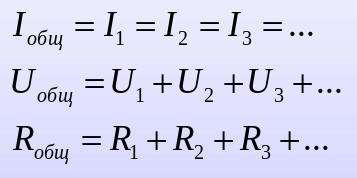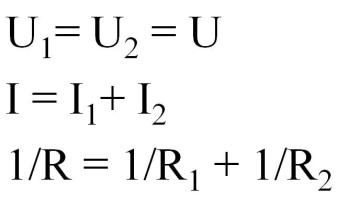Відділ освіти
Покровської районної
державної адміністрації
Великомихайлівська ЗОШ
І-ІІІ ступенів

Задачі на обчислення опорів
провідників
і методи їх розв’язування
КРИЗЬКА С. І.
2015
У брошурі розроблені методи розв’язування задач на обчислення опорів провідників, показано, як ними користуватися для розв’язування конкретних задач.
Задачник може бути рекомендований учням старших класів загальноосвітніх шкіл для підготовки до уроків по темі «Електричний струм» та для підготовки до ЗНО.
Електричний опір
Постійний струм у металевих провідниках являє собою спрямований рух вільних електронів в замкнутому колі.
Направленому руху електричних зарядів в будь-якому провіднику перешкоджають молекули і атоми цього провідника. Тому як зовнішній ділянці ланцюга, так і внутрішній (всередині самого джерела енергії) чинять перешкоду проходженню струму. Величина, що характеризує протидію електричного кола проходження електричного струму, називається електричним опором.
Джерело електричної енергії, включене у замкнене електричне коло, витрачає енергію на подолання опору зовнішнього і внутрішнього кіл.
Електричний опір позначається літерою R. Одиницею вимірювання опору є Ом.
Омом називається електричний опір такого лінійного провідника, в якому при незмінній різниці потенціалів в один Вольт протікає струм силою в один Ампер, тобто 1 Ом = 1 В / 1 А.
В різних речовинах міститься різна кількість вільних електронів, а атоми між якими ці електрони переміщаються, мають різне розташування. Тому опір провідників електричному струму залежить від матеріалу, з якого вони виготовлені, від довжини і площі поперечного перерізу провідника. Якщо порівняти два провідника з одного і того ж матеріалу, то більш довгий провідник має більший опір при рівних площах поперечних перерізів, а провідник з великим поперечним перерізом має менший опір при різних довжинах.
Для відносної оцінки електричних властивостей матеріалу провідника служить його питомий опір. Питомий опір – це опір металевого провідника довжиною 1 м і площею поперечного перерізу 1 мм2, позначається буквою р і вимірюється в  .
.
Якщо провідник, виготовлений з матеріалу з питомим опором р, має довжину 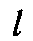 метрів і площу поперечного перерізу S квадратних міліметрів, то опір цього провідника
метрів і площу поперечного перерізу S квадратних міліметрів, то опір цього провідника
.
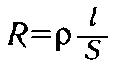
Формула показує, що опір провідника прямо пропорційний питомому опору матеріалу, з якого він виготовлений, а також його довжині і обернено пропорційний площі поперечного перерізу.
Послідовне з'єднання опорів
Електричне коло може містити декілька приймачів енергії, що мають різні опори.
При послідовному з'єднанні провідників кінець попереднього провідника з'єднується з початком наступного.
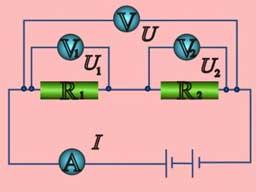
Якщо п провідників опором R1, R2, ... , Rп з'єднані між собою послідовно, то через провідники тече однаковий струм і напруга U0 на кінцях з'єднання дорівнює сумі напруг на окремих провідниках: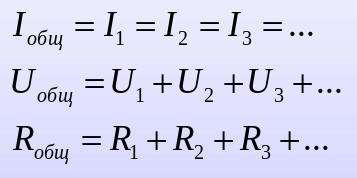
При послідовному з’єднані п провідників з однаковим опором R1, їх загальний R опір дорівнює Rп = п R.
Паралельне з’єднання опорів
Якщо початки провідників з’єднані в одній точці (вузлі), а кінці в іншій, з’єднання провідників називають паралельним.

При паралельному з’єднанні 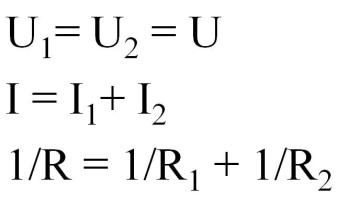
При паралельному з’єднані п провідників з однаковим опором R1, їх загальний R опір дорівнює Rп = R1 / п.
Розв’язування задач на обчислення опорів окремих провідників і різних з’єднань із них
Якщо в умові задачі вказано, із якого матеріалу виготовлений провідник, або наводяться дані про його геометричні розміри або масу, то для знаходження невідомої величини, від якої залежить опір провідника, необхідно використати формулу опору і відношення між масою, густиною і об’ємом провідника.
Під час обчислення загального опору будь-якого контуру, складеного із декількох провідників, необхідно перш за все встановити, чи є в ньому провідники, з’єднані між собою послідовно чи паралельно, чи в схемі таких під’єднань немає.
У першому випадку розв’язують задачі за формулами поданими вище. У другому випадку – необхідно використовувати нові методи розрахунку, в яких формули опору грають фактично не головну, а додаткову роль.
Розв’язування задач на розрахунок опору складних з’єднань необхідно починати із аналізу схеми и знаходження в ній яких-небудь двох провідників, з’єднаних один з одним послідовно або паралельно. При цьому весь час потрібно слідкувати за тим, щоб у випадку послідовного з’єднання струм між провідниками не роз’єднувався, а у випадку паралельного – їх кінці обов’язково з’єднувалися. Якщо у схемі вдається знайти такі провідники, їх опори необхідно замінити одним еквівалентним опором, використовуючи формули записані вище, і одержать спрощену схему. В схемах, які представляють собою комбінацію послідовно і паралельно ввімкнених провідників, цей прийом треба використати декілька раз і таким чином знайти її загальний опір.
Якщо в контурі не знайдеться ні послідовно, ні паралельно з’єднаних провідників, для визначення загального опору використовують слідуючі дві властивості електричного кола:
1) У будь-якому електричному колі точки з однаковим потенціалом можна з’єднати і роз’єднати. Режим струму від цього не змінюється, бо струм між такими точками не проходить.
2) Робота по переміщенню одиничного заряду із однієї точки однорідного кола в іншу не залежить від опорів провідників, по яким проходить заряд, а визначається лише різницею між цими точками.
Іншими словами, який би ми не вибрали шлях руху заряду по однорідному колу, алгебраїчна сума спаду напруги на окремих ділянках цього кола рівна різниці потенціалів між початковою і кінцевою точками.
При цьому необхідно пам’ятати, що таке твердження справедливе лише у тих випадках, коли на заряди діють тільки електричні сили і на ділянках немає ЕРС.
Якщо виясниться, що в схемі немає ні послідовно, ні паралельно з’єднаних провідників, необхідно встановити точки з однаковими потенціалами. Точки з однаковими потенціалами завжди є в схемах, які мають вісь чи площину симетрії відносно точок підключення джерела струму. Тут розрізняють два випадки.
Якщо схема симетрична відносно осі (площини), що проходить через точки входу і виходу струму (є поздовжня площина симетрії), то точки одного потенціалу знаходяться на кінцях симетричних резисторів, оскільки по них проходить однаковий струм.
Якщо схема симетрична відносно осі (площини), яка перпендикулярна лінії, на якій лежать точки входу і виходу струму – в схемі є поперечна вісь (площина) симетрії, то однаковий потенціал мають всі точки, що лежать на перетині цієї осі (площини) з провідниками.
Знайшовши в схемах точки з однаковим потенціалом, треба з’єднати їх (якщо вони були роз’єднані), після цього, як правило, можна одержати еквівалентну схему, складену із послідовно і паралельно з’єднаних резисторів.
Приклади розв’язування задач
Обчислити загальний опір кола в схемах, вказаних на рисунках.
** Два провідники ав і вс з’єднані послідовно, бо між ними немає розгалудження струму.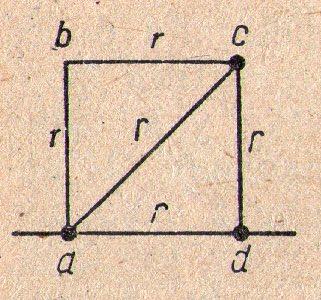
Крім цієї пари, в контурі більше немає двох провідників, які були б з’єднані послідовно чи паралельно. Провідники аd і сd не з’єднані послідовно, бо між ними є струмопровідний провідник, і як наслідок струм між провідниками може розгалуджуватися.
Замінивши ці два резистори одним еквівалентним резистором, опором R1 = 2 R, бачимо, що він підключений паралельно до провідника ас, бо їх кінці мають вузли.
Знаходимо загальний опір R2 провідників R1 і R (контура авсd при включені його в точках а і с)
1/R2 = 1/ R1 + 1/ R, звідси R2 = 2/3 R.
Цей контур з’єднаний послідовно із
провідником сd, і їх загальний опір
R3 = R2 + R = 2/3 R + R = 5/3 R.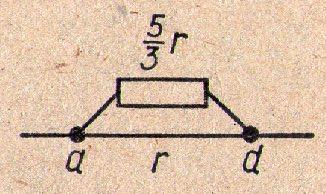
Провідник з опором R3 під’єднаний паралельно до резистора аd. Їх загальний опір (і як наслідок опір всього кола) дорівнює 1/R0 = 1/ R3 + 1/ R = 5/8 R.
** На перший погляд у схемі немає ні послідовних, ні паралельних з’єднань. Резистори опором R і 3 R не є з’єднаними послідовно, бо між ними підключений провідник опором 2 R. Провідники опором R і R (або 3 R і 3 R) не є паралельно з’єднаними, бо точки в і d замкнені провідником опором 2 R.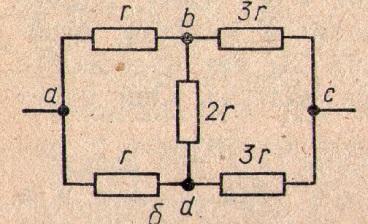
Дану електричну схему часто зображують у такому вигляді: 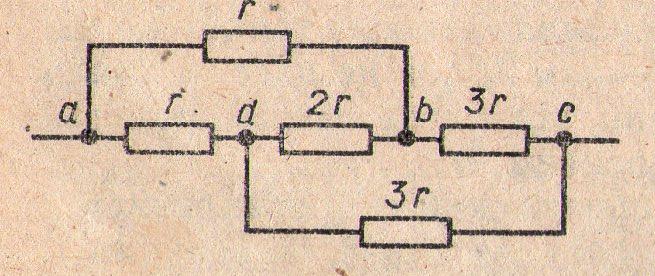
В даній схемі провідники ввімкнені симетрично – в схемі є поздовжня вісь симетрії, що проходить через точки а і с. Тому для обчислення загального опору контуру треба знайти точки з однаковим потенціалом і, роз’єднавши їх (або об’єднавши), підвести задачу до типу попередньої. Якщо струм підійде до вузла а (або с), він розділиться на дві рівні частини, бо умови його проходження по кожній вітці до точки с будуть ідентичними. Потенціали в точках в і d будуть однакові, бо спад напруги на провідниках опором R і R однаковий, і потенціал цих провідників в точці а один той самий. Різниця потенціалів між точками в і d дорівнює нулю, по резистору опором 2 R. Струм не проходить , і, не порушуючи режиму роботи кола, ці точки можна роз’єднати, викинувши провідник опором 2 R
Після такого спрощення схеми провідники опором R і 3 R будуть з’єднаними послідовно, а верхня та нижня вітки – паралельно. Загальний опір всього кола дорівнює
1/ R0 = 1 / (R + 3 R) + 1 / (R + 3 R) = 1 / 2 R
R0 = 2 R.
Роз’єднувати точки в і d , викинувши ввімкнений між ними провідник, можливо лише в тих випадках, коли схема симетрична. Якщо ж, наприклад, в одній із віток помінять місцями резистори опором R і 3 R, то різниця потенціалів між точками в і d не буде дорівнювати нулю; по провіднику 2R пройде струм, і вказаним методом розрахунку скористатися буде не можливо.
Розрахунок опору
Задача 1. Знайти опір кола, якщо R1 = R2 = R3 = 2 Ом.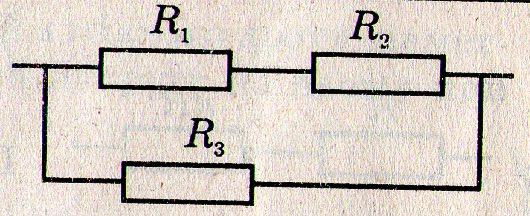
Розв’язання: Резистори з опорами R1 і R2, які з’єднані послідовно, можна замінити одним провідником із опором R 12:
R 12 = R1 + R2 = 2 Ом + 2 Ом = 4 Ом.
Провідники R12 та R3 паралельно з’єднані між собою; знаходимо загальний опір кола:
1/ R0 = 1/ R12 +1/ R3 = 1 / 4 + 1 / 2 = 3 / 4,
R0 = 4 / 3 Ом.
Відповідь: 4 / 3 Ом.
Задача 2. Визначити опір кола, якщо R1 = R2 = R3 = R4 = 4 Ом.
Розв’язання: Резистори 1, 2 , які з’єднані послідовно, можна замінити еквівалентним провідником із опором R12: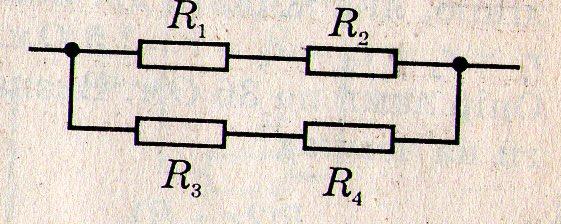
R12 = R1 + R2 = 4 + 4 = 8 Ом, а резистори 3, 4 провідником із опором R34:
R34 = R12 = 8 Ом.
Ці провідники між собою з’єднані паралельно, тому загальний опір кола 1 / R0 = 1 / R12 +1 / R34 = 1/ 8 + 1 / 8 = 1 / 4
R0 = 4 Ом
Відповідь: 4 / 3 Ом.
Задача 3*. Визначити опір кола, якщо R1 = R2 = R5 = R6 = 3 Ом, R3 = 20 Ом, R4 = 24 Ом.
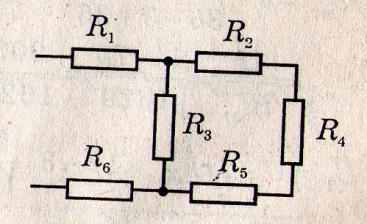
Розв’язання: Резистори з опорами R2, R4, R5 з’єднані послідовно, їх можна замінити одним резистором опором R245:
R245 = R2 + R4 + R5 = 3 Ом + 24 Ом + 3 Ом = 30 Ом.
Резистори з опорами R245 та R3 з’єднані між собою паралельно і їх загальний опір:
1 / R2453 = 1 / R3 + 1 / R245 = 1 / 20 + 1 / 30 = 5 / 60
R2453 = 12 Ом.
Резистори 1 та 6 із резистором 2453 з’єднані послідовно, то загальний опір кола дорівнює:
R0 = R2453 + R1 + R6 = 12 Ом + 3 Ом + 3 Ом = 18 Ом.
Відповідь: 18 Ом.
Задача 4*. Визначити опір електричного кола, якщо
R1 = R2 = R3 = 6 Ом.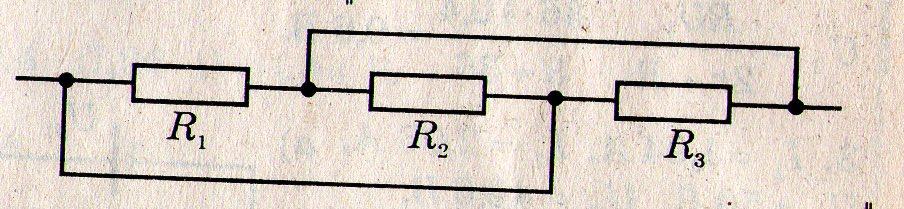
Розв’язання: Дану електричну схему можна подати у вигляді:

Відповідно: 1 / R0 = 1 / R1 + 1 / R2 + 1 / R3 = 1 / 6 + 1 / 6 + 1 / 6 = 1 / 2
R0 = 2 Ом
Відповідь: 2 Ом
Задача 5. На скільки рівних частин треба поділити однорідний провідник з опором R = 36 Ом, щоб опір його частин, з’єданих паралельно, був R0 = 1 Ом?
Розв’язання: Нехай опір однієї частини R1, п – їхня кількість, тоді R1 = R / п.
Якщо з’єднати п частин паралельно, то опір буде дорівнювати
1 / R0 = 1 / R1 • п, R1 = R0• п
R / п = R0• п
R = R0• п2, п = = = 6.
Відповідь: 6
Задача 6. Чому дорівнює опір в схемі між точками А і В?
R1 = R3 = 10 Ом, R2 = R4 = R5 = 5 Ом.
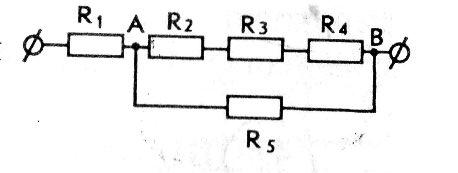
Розв’язання:
Резистор 1 розміщений поза ділянки АВ, тому при визначені опору в схемі між точками А і В, його опір не враховуємо.
Резистори 2,3,4 між собою з’єднані послідовно, тому їх загальний опір дорівнює:
R234 = R2 + R3 + R4 = 5 Ом + 10 Ом + 5 Ом = 20 Ом, а з резистором 5 – паралельно. Обчислимо опір між точками А і В:
1 / RАВ = 1 / R234 + 1 / R5 = 1 / 20 Ом + 1 / 5 Ом = 5 / 20 Ом = 1 / 4 Ом
RАВ = 4 Ом.
Відповідь: 4 Ом.
Задача 7*. Чому дорівнює опір Rх, якщо R1 = R4 = 3 Ом,
R2 = R3 = 10 Ом, а опір всього кола 10 Ом?
Розв’язання: Резистори 2, х, 3 замінимо еквівалентним резистором з опором R2х3

1 / R2х3 = 1 / R2 + 1 / х + 1 / R3 =1 / 10 Ом + 1 / х + 1 / 10 Ом (*).
Резистори 1, 4 та 2х3 з’єднані послідовно, їх загальний опір:
R = R1 + R2х3 + R4
10 Ом = 3 Ом + R2х3 + 3 Ом
R2х3 = 4 Ом.
Значення R2х3 = 4 Ом підставляємо у вираз (*) і одержуємо:
1 / 4 Ом =1 / 10 Ом + 1 / х + 1 / 10 Ом
1 / х = 1 / 20 Ом
х = 20 Ом.
Відповідь: 20 Ом.
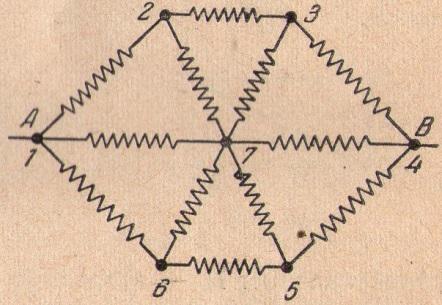
Задача 8*. Коло складено з 9 однакових резисторів. Опір усього кола між точками А і В дорівнює 1,5 Ом. Який опір кожного з резисторів?
Розв’язання
1) Знайдемо опір з’єднання 124:
1 / R12 == 1 / 2 R + 1 / R = 3 / 2 R
R12 = 2 R / 3;
R124 = R12 + R = 2 R / 3 + R = 5 R / 3.
2) З’єднання 124 та 134 – симетричні відносно провідника АВ, тому
R124 = R134 = 5 R / 3.
3) Знайдемо опір між точками АВ:
1 / RАВ = 1 / R124 + 1 / R134 + 1 / R = 3 / 5 R + 3 / 5 R + 1 / R = 11 / 5 R
RАВ = 5 R / 11.
За умовою задачі опір усього кола між точками А і В дорівнює 1,5 Ом, тому можемо знайти опір R1 кожного з резисторів:
1,5 Ом = 5 R / 11
R1 = (11 • 1,5 Ом) / 5 = 3,3 Ом.
Відповідь: 3,3 Ом.
Задача 9*. Знайти опір між точками АВ, якщо R1 = 4 Ом, R2 = 4 Ом, R3 = 5 Ом, R4 = 3 Ом, R5 = 1,5 Ом, R6 = 2 Ом.
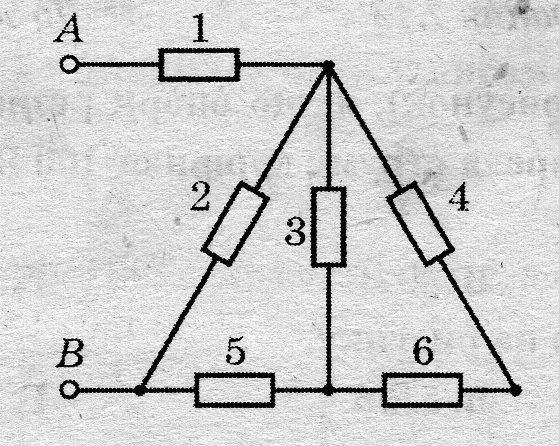
Розв’язання:
Дану електричну схему можна замінити

1) Rа46в = R4 + R6 = 3 Ом + 2 Ом = 5 Ом;
1 / Rав = 1 / Rа46в + 1 / R3 = 1 / 5 Ом + 1 / 5 Ом = 2 / 5 Ом,
Rав = 5 Ом / 2 = 2,5 Ом.
2) Rавс = Rав + R5 = 2,5 Ом + 1,5 Ом = 4 Ом;
1 / Rас = 1 / Rавс + 1 / R2 = 1 / 4 Ом + 1 / 4 Ом = 1 / 2 Ом,
Rас = 2 Ом.
3) RАВ = R1 + Rас = 4 Ом + 2 Ом = 6 Ом.
Відповідь: 6 Ом.
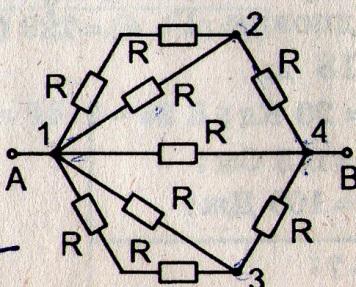
Задача 10*. Знайти опір шестикутника, якщо він ввімкнений в коло між точками А і В. Опір кожного провідника дорівнює R.
Розв’язання: 1) Внаслідок симетрії опір шестикутника не зміниться, якщо від’єднати провідники 2-7, 7-3, 6-7, 5-7 від центра. Опори, утворених верхньої і нижньої частин схеми, рівні.
2) Знайдемо опір верхньої частини схеми: R273 = R + R = 2R;
1 / R23 = 1 / R + 1 / 2R = 3 /2R, R23 = 2R / 3;
R1234 = R + 2R / 3 + R = 8 R / 3.
3) Знайдемо опір шестикутника, якщо верхня його частина, нижня та провідники 1-7-4 з’єднані між собою паралельно:
1 / RАВ = 1 / R1234 + 1 / R1654 + 1 / R174 = 3 / 8 R + 3 / 8 R + 1 / 2R = 5 / 4R,
RАВ = 4R / 5.
Відповідь: 4R / 5.
Задача 11. Визначити загальний опір з’єднання, кожен елемент якого має опір R.
а)
Розв’язання: Резистори закорочені, тому опір з’єднання дорівнює нулю.
б)
Розв’язання: Верхні два послідовно з’єднані резистори, приєднані до третього паралельно. Загальний опір з’єднання:
1 / R0 = 1 / R + 1 / 2 R = 3 / 2 R.
в)
Розв’язання: Третій резистор з’єднання закорочений, тому його опір дорівнює нулю. А перші два провідники з’єднані паралельно, і їх опір
R0 = R / 2.
г)
Розв’язання: Різниця потенціалів між верхньою і нижньою точками дорівнює нулю, по резистору, що розміщений в центрі схеми. Струм не проходить, і, не порушуючи режиму роботи кола, ці точки можна роз’єднати, викинувши цей провідник. Після такого спрощення схеми провідники, що розміщені вгорі (внизу) є з’єднаними послідовно, а верхня та нижня вітки – паралельно.
1 / R0 = 1 / 2R + 1 / 2R = 1 / R
R0 = R.
д)
Розв’язання: Дану електричну схему можна замінити так, як показано на рисунку:
1) Знайдемо опори з’єднання 1 та 3: R1 = R3 = R / 2.
2) Знайдемо опір з’єднання а-в:
1 / 2R + 1 / 2R = 1 / R
1 / R АВ = 1 / R + 1 / R = 2 / R
R АВ = R / 2.
3) Опір усієї електричної схеми: R0 = R / 2 + R / 2 + R / 2 = 3 R / 2
е)
Розв’язання: Електричну схему можна зобразити у вигляді:
1) По провіднику а струм не проходить, і він не впливає на опір фігури. Фігура розділяється на дві симетричні частини відносно осі АВ. Вони з’єднані між собою паралельно.
2) Опір однієї частини:
- опір з’єднання 1 або з’єднання 2 дорівнює
1 / R1 = 1 / R + 1 / 2 R = 3 /2 R, R1 = R2 = 2 R / 3.
- опір лівої частини електричної схеми (з’єднання 1 та 2, резистор в приєднанні один до одного послідовно)
R12в = R1 + R2 + Rв = 2 R / 3 + 2 R / 3 + R = 7 R / 3.
- опір всієї фігури R0 = 7 R / 3 ÷ 2 = 7 R / 6.
Відповідь: 0, 3 / 2 R, R / 2, R, 3R / 2, 7 R / 6.
Задача 12*. П’ять однакових нікелінових стержнів довжиною l з’єднані мж собою у вигляді зірки. Точками з’єднання кожний стержень поділяється на три однакові частини (АВ = ВД = ДЕ =…). Визначити опір цієї фігури між точками А і F. Площа поперечного перерізу стержня S, питомий опір нікеліну p.
Розв’язання: Задачу розв’язуємо аналогічно до задачі 11 г.
1) Опір стержня:
Опір однієї частини стержня : R = .
2) Фігура розділяється на дві симетричні частини АВ1С1Д1Е1F і АВСДЕF, які з’єднані паралельно. Опір однієї частини:
R1 = RАВ1 + RВ1С1ДІ + RД1Е1F = RАВ1 + 2 RВ1С1ДІ,
1 / RВ1С1ДІ = 1 / 2R1 + 1 / R1 = 3 / 2R1 = 3 / 2 ÷ рl / 3S = 9 S / 2 рl
RВ1С1ДІ = 2 рl / 9 S.
R1 = рl / 3S + 2 • 2 рl / 9 S = 7 рl / 9 S.
3) Опір всієї фігури:
R0 = 7 рl / 9 S • 1 /2 = 7 рl / 18 S.
Відповідь: 7 рl / 18 S
Задача 13*. Три однакові мідні кільця радіусом R з’єднані між собою так, як показано на рисунку. Визначити опір r електричному струмові одержаної таким чином фігури, якщо зовнішня різниця потенціалів підведена до точок А і В. Діаметр дротини d. Питомий опір міді р.
Розв’язання: Внаслідок симетрії фігури потенціали точок С, F, Д, Е дорівнюють один одному, і тому кільце СДЕFС на опір фігури не впливає, і його можна викинути із схеми. Визначення опору зводиться до знаходження опору паралельного з’єднання чотирьох провідників.
-
Довжина кожного провідника: lкола / 2 = 2 πR,
-
Опір одного провідника: r1 = рl / S = р πR ÷ π d2 / 4 = 4 рR / d2 .
Таких провідників чотири і вони з’єднані паралельно, то
r = r1 / 4 = 4 рR / d2 ÷ 4 = рR / d2 .
Відповідь: рR / d2.
Література
1. Балаш В.А. Задачи по физике и методы их решения.
2. Задачник по физике. А. Н. Волохов, А. А. Воробьев, М. Ф. Федоров, А. Г. Чертов.
3. Гончаренко. С. У. Гончаренко. Конкурсні задачі з фізики.
4. Збірник різнорівневих завдань для державної підсумкової атестації з фізики. І. М. Гельфгат: Гімназія, Х., 2002
5. Збірник різнорівневих завдань з фізики для диференційованого контролю знань учнів. В. Л. Головань, Дніпропетровськ, 1997
6. Фізика. Завдання для поточного оцінювання. 10 клас. О. С. Іллєнко. Х., 2004
7. Китаев В. Е., Шляпинтох Л. С. Электротехника с основами промышленной электроники.
Зміст
1. Електричний опір 3
2. Послідовне з'єднання опорів 4
3. Паралельне з’єднання опорів 5
4. Розв’язування задач на обчислення опорів окремих провідників і різних з’єднань із них 5
5. Приклади розв’язування задач 7
6. Розрахунок опору 10
7. Література 25
16