Презентация "Число е и его применение в финансовых расчетах"

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВОРОНЕЖСКОЙ ОБЛАСТИ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПРОМЫШЛЕННО-ГУМАНИТАРНЫЙ КОЛЛЕДЖ» Число е и его применение в финансовых расчетах Номинация 4. Использование математических методов для решения профессионально ориентированных задач

Выполнила Ситникова Екатерина Сергеевна

Руководитель Латышева Надежда Леонидовна

ЦЕЛЬ РАБОТЫ:

Рассмотреть сущность и различные подходы к определению числа е, а так же его использование в финансовых расчетах.

Число e   — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828.

Символ  e   для обозначения этого числа был введен в 1731 Л.Эйлером (1707–1783).

Саму же константу впервые вычислил швейцарский математик  Якоб Бернулли  в ходе решения задачи о предельной величине процентного дохода . Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел, равный е.

Существует несколько подходов к

определению числа е:

1. ЧЕРЕЗ УГЛОВОЙ КОЭФФИЦИЕНТ ПРЯМОЙ; 2. ЧЕРЕЗ ПРОИЗВОДНУЮ; 3. ЧЕРЕЗ ИНТЕГРАЛ; 4. ЧЕРЕЗ ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ; 5. ЧЕРЕЗ СУММУ РЯДА.

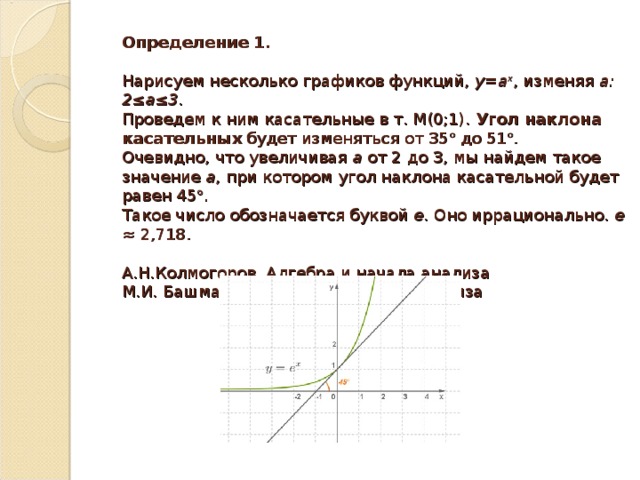
Определение 1. Нарисуем несколько графиков функций, y = a x , изменяя а: 2≤а≤3. Проведем к ним касательные в т. М(0;1). Угол наклона касательных будет изменяться от 35  до 51  . Очевидно, что увеличивая а от 2 до 3, мы найдем такое значение а , при котором угол наклона касательной будет равен 45  . Такое число обозначается буквой е . Оно иррационально. е ≈ 2,718. А.Н.Колмогоров. Алгебра и начала анализа М.И. Башмаков. Алгебра и начала анализа

Определение 2. Производная , т.е. скорость роста, показательно функции пропорциональна самой этой функции: (а х )′= k·a x Число е – это такое основание показательной функции, для которой коэффициент пропорциональности k = 1, т.е. производная функции y = e x на самой этой функции: (е х )′=е x М.И. Башмаков Алгебра и начала анализа

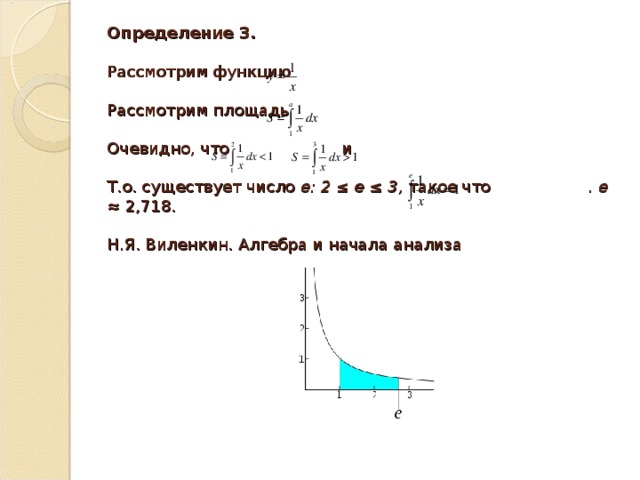
Определение 3. Рассмотрим функцию Рассмотрим площадь Очевидно, что и Т.о. существует число е: 2 ≤ е ≤ 3, такое что . е ≈ 2,718. Н.Я. Виленкин. Алгебра и начала анализа

Определение 4. Рассмотрим последовательность x n = (1+1/ n ) n . x n = {2; 2,25; 2,37; 2,44; …} Эта последовательность монотонно возрастает и ограничена (можно доказать, что x n е. А.Г. Цыпкин. Справочник по математике

Определение 5. Число е – иррациональное число, приблизительно равное 2,718. Его можно представить как сумму: Ш.А. Алимов. Алгебра и начала анализа

Число е находит применение в интегральном и дифференциальном исчислении, а так же в естественных науках. Например, при распаде радиоактивного вещества по истечении времени  t  от исходного количества вещества остается доля, равная  e –kt , где  k  – число, характеризующее скорость распада данного вещества.  Затухание электрического тока   I  в простом контуре с последовательным соединением, сопротивлением  R  и индуктивностью  L  происходит по закону  I = I 0 e –kt , где  k = R/L ,  I 0  – сила тока в момент времени  t  = 0. Аналогичные формулы описывают релаксацию напряжений в вязкой жидкости и затухание магнитного поля . Аналогично, если бактерии в питательной среде размножаются со скоростью, пропорциональной их числу в настоящий момент, то по истечении времени  t  начальное количество бактерий   N  превращается в  Ne kt .

Применение в финансовых расчетах. В практических банковских расчетах в основном применяют дискретные проценты , т.е. проценты, начисляемые за фиксированный промежуток времени (год, полугодие, квартал и т.д.). В некоторых случаях — для экономического анализа и в расчетах, связанных с непрерывными процессами, в математическом моделировании, а иногда и на практике — возникает необходимость в применении непрерывных процентов .

В финансовой математике увеличение суммы денег в результате начисления сложных процентов определяется формулой: FV=PV(1+j / m) mn где PV – исходная сумма денег FV – наращенная сумма денег n – число лет, соответствующее сроку финансовой операции j – ставка процентов за год m – число периодов начисления в году Чем больше m , тем чаще начисляются проценты. Способ начисления процентов, при котором m  , называется непрерывным начислением процентов.

В этом случае: Полученную формулу обычно записывают в виде: где S 0 – начальная сумма денег. В этой формуле величина δ характеризует скорость роста суммы. Ее называют  силой роста , или  силой процента . Она равна скорости относительного прироста суммы, т. е. равна относительному приросту суммы за бесконечно малый промежуток времени. 

Пример. Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%? Решение:

Пример. Пусть темп инфляции составляет 1% в день. Во сколько раз уменьшится первоначальная сумма через полгода? Решение: Т.о. инфляция уменьшит первоначальную сумму примерно в 6 раз.

ВЫВОД:

Удивительно, но число е настолько многогранно, что к нему можно прийти, рассматривая самые разные математические задачи.

Число е играет огромную роль в математике и прикладных науках.

В банковском деле оно позволяет определять прирост денег при непрерывном начислении процентов.

Использованная литература: Алимов Ш.А. и др. Алгебра и начала анализа. 10-11 кл. Учебник для общеобразовательных учреждений. - М.:Просвещение, 2014. Башмаков М.И . Алгебра и начала математического анализа (базовый уровень). 10-11 кл. – М.:Просвещение, 2012. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и начала математического анализа. 11 класс. Углубленный уровень.  18-е изд., стер. - М.: 2014. -  312 с.  Капитоненко В.В. Задачи и тесты по финансовой математике : учеб. пособие / В.В. Капитоненко. – М. : Финансы и статистика, 2014. – 256 с. : ил. Колмогоров А.Н. и др. Алгебра и начала анализа. 10-11 кл. – М.:Просвещение, 2014. Красс М.С., Чупрынов Б.П. Математика для экономистов. – СПб.: Питер, 2014. – 464 с. Цыпкин А.Г. Справочник по математике для средних учебных заведений, 1983