Числовая последовательность

Числовая последовательность

Вступление

Историческая справка

Логические задачи

Определение

числовой последовательности

Способы задания последовательности

График последовательности

Примеры решения задач

Математический диктант

Домашнее задание № 1 № 2 Повторение

Щелчком мыши на строчку перечисления переход на данный вопрос.

Можно вернуться к оглавлению управляющей кнопкой или перейти на следующий слайд.

• Натуральный ряд чисел:

• 1, 2, 3, 4, 5, 6, 7, 8, … демонстрирует

упорядочение по возрастанию в чистом виде.

• Принцип построения следующей цепочки чисел не так очевиден: 1, 1, 2, 3, 5, 8, 13, 21, …, хотя они тоже стоят не хаотично: каждое число, начиная с третьего, равно сумме двух предшествующих.
• Этому ряду натуральных чисел, имеющему своё историческое название – ряд Фибоначчи , присуща своя логика и красота, постижение которой возможно только при целенаправленном изучении.

• ЧИСЛА ФИБОНАЧЧИ.

• Леонардо Фибоначчи (1170-1250),

или Леонардо Пизанский, или

Фибоначчи – сын Боначчо.

• Крупный итальянский математик,

автор «Книги абака».

• Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!).

Логические задачи

• а) . Продолжи последовательности чисел:

• 0, 1, 2, 3, 0, 1, …

• 2, 3, 0 – каждый член равен остатку от деления его номера на 4

• 1, 2, 2, 4, 8, …

• 32, 256, 8192 – произведение 2-х предыдущих членов последовательности

Нажатием клавиши «пробел» или щелчком мыши открывается решение задания

Логические задачи

• б) Поменяйте местами две цифры так, чтобы в каждой строке образовались два новых пятизначных числа, причём одно – в два раза больше второго.

4

2

5

5

9

9

0

8

8

0

6

1

6

1

3

3

7

7

2

4

каждое число в совокупности имеет вполне определенный № и полностью им определяется. " width="640"

Определение числовой последовательности

• Рассмотрим следующую совокупность чисел:
• 1) 1, 2, 3, 4, … n , … натуральные числа
• 2) 2, 4, 6, … 2 n , … положительные четные числа по возрастанию
• 3) аликвотные дроби
• Естественно считать, что каждое число в любой последовательности снабжено №

в соответствии с тем местом, которое оно занимает в этой совокупности,

= каждое число в совокупности имеет вполне определенный № и полностью им определяется.

• Опр.1. Совокупность чисел, каждое из которых снабжено своим №, называется числовой последовательностью.
• Обозначение: { a n }

• Отдельные числа последовательности называются ее членами.

• a n – общий член последовательности.

• Задать числовую последовательность – это значит указать, как найти тот или иной ее член, если известен № занимаемого им места.

• Опр. 1. 2. (в матанализе)

• Функцию y = f(x), определённую на множестве натуральных чисел хєN (или его конечном подмножестве), называют числовой последовательностью и обозначают
• y = f(n), или у 1 , у 2 ,… , у n , …, или (у n ).
• Индекс n определяет порядковый № члена последовательности.
• Значения у 1 , у 2 , …, у n называют соответственно I , II , …, n-членами последовательности.

• Различают конечные и бесконечные числовые последовательности.

• Опр.2. Последовательность, состоящая из конечного числа членов, называется конечной, а – из бесконечного числа членов – бесконечной.

• 2, 4, 6, 8, 10 - конечная
• 2, 4, 6, 8, 10, … - бесконечная

Способы задания последовательности

• 1. Аналитический:

• указывается формула n-го члена последовательности.

• Пример. Последовательность квадратов натуральных чисел

• 1, 4, 9, 16, … задаётся формулой у n =n 2 .

• С помощью формулы n - го члена можно вычислить любой член последовательности, подставив в формулу вместо n номер № вычисляемого члена.

• Пример. Если ,

• то при n=2
• ( II член последовательности),
• при n=20
• и т.д.

• Опр.3. Формула, позволяющая найти любой член последовательности по его №, называется формулой общего члена последовательности.

• 2. Словесный:

• правило составления последовательности выражается словесным описанием.

• Примеры.

• 1) Последовательность простых двузначных чисел, меньших 50, есть конечная последовательность:

• 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47;

• 2) Бесконечная последовательность приближений иррационального числа

• 1,4; 1,41; 1,414; 1,4142; …

• Иногда в подобных случаях вообще нельзя установить формулу a n , тем не менее, последовательность оказывается полностью определенной.

• 3. Рекуррентный:

• указывается правило, позволяющее вычислить n-й член данной последовательности, если известны все её предыдущие члены.
• Иногда указывается несколько первых членов последовательности, а все остальные определяются этими заданными числами по тому или иному правилу.

• Примеры.

• 1) у 1 = 1, у n = у n-1 ∙ n, если n ≥ 2.
• Вычислим несколько первых членов этой последовательности: 1, 2, 6, 24, 120, … .
• Можно убедиться в том, что n-й член данной последовательности равен произведению первых n натуральных чисел: у n = n!

1, 1, 2, 3, 5, 8, 13, 21, 34, … - числа Фибоначчи Опр.4. Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной. Лат. r ecurro – возвращаться. " width="640"

• 2) а 1 = 1, а 2 = 1, а каждый последующий член определяется как сумма 2-х предыдущих, т.е. при
• = 1, 1, 2, 3, 5, 8, 13, 21, 34, … - числа Фибоначчи

• Опр.4. Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной.

• Лат. r ecurro – возвращаться.

График последовательности

• Графиком последовательности как функции, заданной на множестве натуральных чисел, являются отдельные, изолированные точки координатной плоскости.

• Примеры:

• 1) последовательность у n =3n-2 можно рассматривать как функцию у=3х-2, где хєN;
• 2) Последовательность у n =n 2 можно рассматривать как функцию у=х 2 , где хєN.

-2, -2, 0, 4, 10 № 2. x n = (-1) n · 10, определить последовательность Решение: все члены последовательности будут с нечетными № (-10), а с четными № - (10) -10, 10, -10, 10, -10, … Нажатием клавиши «пробел» или щелчком мыши открывается решение задания " width="640"

Примеры решения задач

• № 1. a n = n 2 – 3 n , найти
• Решение:

• подставим вместо n натуральные числа - № члена последовательности
• а 1 = 1 2 - 3·1 = -2, … = -2, -2, 0, 4, 10

• № 2. x n = (-1) n · 10, определить последовательность
• Решение:

• все члены последовательности будут
• с нечетными № (-10), а с четными № - (10)
• -10, 10, -10, 10, -10, …

Нажатием клавиши «пробел» или щелчком мыши открывается решение задания

• № 3. Укажите номер функции, являющейся числовой последовательностью:
• 1)

• 2) 3)
• Решение:

• Функции 1) и 3) не являются числовыми последовательностями, так как они не заданы на множестве N - натуральных чисел.
• Функция 2) является числовой последовательностью, так как она задана на множестве N - натуральных чисел.
• Ответ: 2

• № 4. Найдите первые пять членов последовательности, заданной рекуррентно:
• у 1 = 2, у n = у n-1 + 5
• Решение:

• Чтобы определить n-й член последовательности, начиная со второго, нужно в рекуррентную формулу подставить значения предыдущего члена.
• По условию у 1 = 2.
• Для второго члена получим: у 2 = у 1 + 5 = 7. Аналогично у 3 = у 2 + 5 =1 2, у 4 = у 3 + 5 = 17, у 5 = у 4 + 5 = 22.
• Ответ: 2, 7, 12, 17, 22.

• № 5. Является ли число членом
• последовательности ?
• Решение:

• Составим уравнение:
• Решим полученное уравнение относительно переменной n: n = 10. Поскольку 10 – натуральное число,
• то является членом
• последовательности { c n }:
• Ответ: да.

Математический диктант

• Вариант 1 ( 2 )

• 1. Является ли конечной или бесконечной последовательность делителей числа 1200? кратных числа 8?
• 2. Является ли конечной или бесконечной последовательность чисел, кратных 6? делителей числа 2400?
• 3. Последовательность задана формулой

• a n = 5n + 2 ( b n = n 2 - 3 ). Чему равен её III член?

• 4. Запишите последний член последовательности всех трёхзначных ( двузначных ) чисел.
• 5. Дана рекуррентная формула последовательности a n+1 = a n - 4, а 1 = 5
• ( b n+1 = b n / 4, b 1 = 8 ). Найдите a 2 ( b 2 ).

Ответы:

• Вариант 2.

• Вариант 1.

• 1. Бесконечной.
• 2. Конечной.
• 3. 6.
• 4. 99.
• 5. 2.

• 1. Конечной.
• 2. Бесконечной.
• 3. 17.
• 4. 999.
• 5. 1.

• Домашнее задание:
• A., с.52, § 9

• А № 148 - 153.

Дом.задание может быть по учебнику, который используется в конкретном классе…

Последовательности

1) 1; 4; 5; 7; 9; 10; 20; … 5)2 2 ; 3 2 ; 4 2 ;…

2) 1 2 ; 1 3 ; 1 4 ; 1 5 ; . . . size 12{ { {1} over {2} } ; { {1} over {3} } ; { {1} over {4} } ; { {1} over {5} } ; "." "." "." } {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAAdkKAADm AwAAlQAAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAANgKAADlAwAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlv biBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQAC AAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAACEAAAAcgEAAAEAMdMAAAAA AP//AQAxAIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigAB ADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAA AAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAA hAAAANwBAACCAQAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJl cmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAA iAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAIQAAACEAwAAAQAy 0wAAAAAA//8BADIAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRp b24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEA AgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAwgEAAGECAAABADuNAAAA AAD//wEAOwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBT ZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAA AQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAACVAgAAcgEAAAEAMdMAAAAAAP// AQAxAIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwA AAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAA AP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAewIA ANwBAAB+AwAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0 aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAAB AAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAJUCAACEAwAAAQAz0wAA AAAA//8BADMAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24g U2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAA AAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA0wMAAGECAAABADuNAAAAAAD/ /wEAOwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJp ZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCH AAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADBBAAAcgEAAAEAMdMAAAAAAP//AQAx AIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwAAAAD ADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8D AAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAjAQAANwB AAClBQAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9u IFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIA AAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAMEEAACEAwAAAQA00wAAAAAA //8BADQAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2Vy aWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEA hwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA5AUAAGECAAABADuNAAAAAAD//wEA OwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAA AAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEA BQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADSBgAAcgEAAAEAMdMAAAAAAP//AQAxAIwA AQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwAAAADADYA AAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAA AACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAuAYAANwBAAC6 BwAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNl cmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAAB AIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAANIGAACEAwAAAQA10wAAAAAA//8B ADUAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYA AAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwAB AAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA9QcAAGECAAABADuNAAAAAAD//wEAOwCM AAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAA AKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAA AP////8AhgABAAQAAAAAAAAAcgACABcAAACvCAAAYQIAAAEALmoAAAAAAP//AQAuAIwAAQAA AAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEA AAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA//// /wCGAAEABAAAAAAAAAByAAIAFwAAAE0JAABhAgAAAQAuagAAAAAA//8BAC4AjAABAAAAAACL AAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAAD AAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYA AQAEAAAAAAAAAHIAAgAXAAAA7AkAAGECAAABAC5qAAAAAAD//wEALgCMAAEAAAAAAJUAAQAE AAAAAAAAAJYAAQACAAAACQCMAAEAAAAAAA== 6) 1 2 ; 2 3 ; 3 4 ; 4 5 ; . . . size 12{ { {1} over {2} } ; { {2} over {3} } ; { {3} over {4} } ; { {4} over {5} } ; "." "." "." } {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAAfAKAADm AwAAlQAAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAAO8KAADlAwAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlv biBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQAC AAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAACEAAAAcgEAAAEAMdMAAAAA AP//AQAxAIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigAB ADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAA AAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAA hAAAANwBAACCAQAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJl cmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAA iAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAIQAAACEAwAAAQAy 0wAAAAAA//8BADIAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRp b24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEA AgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAwgEAAGECAAABADuNAAAA AAD//wEAOwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBT ZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAA AQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAACVAgAAcgEAAAEAMtMAAAAAAP// AQAyAIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwA AAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAA AP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAewIA ANwBAAB+AwAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0 aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAAB AAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAJUCAACEAwAAAQAz0wAA AAAA//8BADMAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24g U2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAA AAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA0wMAAGECAAABADuNAAAAAAD/ /wEAOwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJp ZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCH AAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADBBAAAcgEAAAEAM9MAAAAAAP//AQAz AIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwAAAAD ADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8D AAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAjAQAANwB AAClBQAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9u IFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIA AAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAMEEAACEAwAAAQA00wAAAAAA //8BADQAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2Vy aWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEA hwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA5AUAAGECAAABADuNAAAAAAD//wEA OwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAA AAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEA BQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADSBgAAcgEAAAEANNMAAAAAAP//AQA0AIwA AQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwAAAADADYA AAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAA AACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAuAYAANwBAADR BwAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNl cmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAAB AIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAANIGAACEAwAAAQA10wAAAAAA//8B ADUAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYA AAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwAB AAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAEAgAAGECAAABADuNAAAAAAD//wEAOwCM AAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAA AKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAA AP////8AhgABAAQAAAAAAAAAcgACABcAAADJCAAAYQIAAAEALmoAAAAAAP//AQAuAIwAAQAA AAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEA AAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA//// /wCGAAEABAAAAAAAAAByAAIAFwAAAGgJAABhAgAAAQAuagAAAAAA//8BAC4AjAABAAAAAACL AAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAAD AAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYA AQAEAAAAAAAAAHIAAgAXAAAA7AkAAGECAAABAC5qAAAAAAD//wEALgCMAAEAAAAAAJUAAQAE AAAAAAAAAJYAAQACAAAACQCMAAEAAAAAAA==

3) − а ; − 1 2 а ; − 1 3 а ; . . . size 12{ - а; - { {1} over {2} } а; - { {1} over {3} } а; "." "." "." } {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAATkOAADm AwAAigAAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAADgOAADlAwAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAIsAAQACAAAAHwCKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJv bAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCH AAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABoAAABqAAAAYQIAAAEAAAASIk8BAAAAAP// AQASIowAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlm AAAAAAAApgEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcA AQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAGAAAAMIBAABhAgAAAgDQsNMAAAAAAP//AQAw BIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAA AAAApgEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAF AAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAMoCAABhAgAAAQA7jQAAAAAA//8BADsAjAAB AAAAAACLAAEAAgAAAB8AigABADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8A AAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYA AQAEAAAAAAAAAHIAAgAaAAAATwMAAGECAAABAAAAEiJPAQAAAAD//wEAEiKMAAEAAAAAAIsA AQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMA AAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgAB AAQAAAAAAAAAcgACABcAAADcBAAAcgEAAAEAMdMAAAAAAP//AQAxAIwAAQAAAAAAiwABAAIA AAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwAAAADADYAAAAKAE9wZW5TeW1i b2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEA hwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAAwQQAANwBAAC/BQAA8AEAAIwAAQAA AAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEA AAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA//// /wCGAAEABAAAAAAAAAByAAIAFwAAANwEAACEAwAAAQAy0wAAAAAA//8BADIAjAABAAAAAACL AAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAAD AAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYA AQAEAAAAAAAAAHIAAgAYAAAA/wUAAGECAAACANCw0wAAAAAA//8BADAEjAABAAAAAACLAAEA AgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAA BQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAE AAAAAAAAAHIAAgAXAAAABwcAAGECAAABADuNAAAAAAD//wEAOwCMAAEAAAAAAIsAAQACAAAA HwCKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8D AAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgAC ABoAAACmBwAAYQIAAAEAAAASIk8BAAAAAP//AQASIowAAQAAAAAAiwABAAIAAAAfAIoAAQBC AAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMA AAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIA FwAAADMJAAByAQAAAQAx0wAAAAAA//8BADEAjAABAAAAAACLAAEAAgAAAB8AhQABAAUAAAAA AAAAAYQAAQAFAAAAAAAAAACKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAAKYBAAD/ /wAAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8A hgABAAQAAAAAAAAAZwABABAAAAAYCQAA3AEAABsKAADwAQAAjAABAAAAAACLAAEAAgAAAB8A igABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAA AAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAA AHIAAgAXAAAAMwkAAIQDAAABADPTAAAAAAD//wEAMwCMAAEAAAAAAIsAAQACAAAAHwCKAAEA QgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAACAP8D AAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgAC ABgAAABWCgAAYQIAAAIA0LDTAAAAAAD//wEAMASMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAA AAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAACAP8DAAAA AAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcA AABeCwAAYQIAAAEAO40AAAAAAP//AQA7AIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8 AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAA AAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAABgM AABhAgAAAQAuagAAAAAA//8BAC4AjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQ AExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8D AAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAtgwAAGEC AAABAC5qAAAAAAD//wEALgCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGli ZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAA AIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAAA7DQAAYQIAAAEA LmoAAAAAAP//AQAuAIwAAQAAAAAAlQABAAQAAAAAAAAAlgABAAIAAAAJAIwAAQAAAAAA 7) 1; 3; 7; 13;…

4) 1 5 ; − 1 5 ; 1 5 ; − 1 5 ; . . . size 12{ { {1} over {5} } ; - { {1} over {5} } ; { {1} over {5} } ; - { {1} over {5} } ; "." "." "." } {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAATUNAADm AwAAowAAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAADQNAADlAwAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlv biBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQAC AAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAACEAAAAcgEAAAEAMdMAAAAA AP//AQAxAIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigAB ADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAA AAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAA hAAAANwBAACGAQAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJl cmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAA iAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAIQAAACEAwAAAQA1 0wAAAAAA//8BADUAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRp b24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEA AgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAwgEAAGECAAABADuNAAAA AAD//wEAOwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJvbAAA AAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEA BQAAAP////8AhgABAAQAAAAAAAAAcgACABoAAABGAgAAYQIAAAEAAAASIk8BAAAAAP//AQAS IowAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAA AAAApgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAF AAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAANMDAAByAQAAAQAx0wAAAAAA//8BADEAjAAB AAAAAACLAAEAAgAAAB8AhQABAAUAAAAAAAAAAYQAAQAFAAAAAAAAAACKAAEAPAAAAAMANgAA AAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAA AIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAZwABABAAAAC5AwAA3AEAALsE AADwAQAAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2Vy aWYAAAAAAACmAQAAAAADAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEA hwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA0wMAAIQDAAABADXTAAAAAAD//wEA NQCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAA AAAAAKYBAAAAAAMAAAAFAAAAAAACAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEA BQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAAAQBQAAYQIAAAEAO40AAAAAAP//AQA7AIwA AQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAA pgEAAAAAAwAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA /////wCGAAEABAAAAAAAAAByAAIAFwAAAOQFAAByAQAAAQAx0wAAAAAA//8BADEAjAABAAAA AACLAAEAAgAAAB8AhQABAAUAAAAAAAAAAYQAAQAFAAAAAAAAAACKAAEAPAAAAAMANgAAAAoA T3BlblN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgA AQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAZwABABAAAADKBQAA3AEAAMwGAADw AQAAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYA AAAAAACmAQAAAAADAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwAB AAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA5AUAAIQDAAABADXTAAAAAAD//wEANQCM AAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAA AKYBAAAAAAMAAAAFAAAAAAACAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAA AP////8AhgABAAQAAAAAAAAAcgACABcAAAAiBwAAYQIAAAEAO40AAAAAAP//AQA7AIwAAQAA AAAAiwABAAIAAAAfAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9sAAAAAAAApgEAAP//AAAA AAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEA BAAAAAAAAAByAAIAGgAAAKYHAABhAgAAAQAAABIiTwEAAAAA//8BABIijAABAAAAAACLAAEA AgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAA BQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAE AAAAAAAAAHIAAgAXAAAAMwkAAHIBAAABADHTAAAAAAD//wEAMQCMAAEAAAAAAIsAAQACAAAA HwCFAAEABQAAAAAAAAABhAABAAUAAAAAAAAAAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9s AAAAAAAApgEAAP//AAAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcA AQAFAAAA/////wCGAAEABAAAAAAAAABnAAEAEAAAABgJAADcAQAAGgoAAPABAACMAAEAAAAA AIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAA AAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8A hgABAAQAAAAAAAAAcgACABcAAAAzCQAAhAMAAAEANdMAAAAAAP//AQA1AIwAAQAAAAAAiwAB AAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAA AAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEA BAAAAAAAAAByAAIAFwAAAFYKAABhAgAAAQA7jQAAAAAA//8BADsAjAABAAAAAACLAAEAAgAA AB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAA AAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAA AAAAAHIAAgAXAAAADwsAAGECAAABAC5qAAAAAAD//wEALgCMAAEAAAAAAIsAAQACAAAAHwCK AAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAA AP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAA cgACABcAAACuCwAAYQIAAAEALmoAAAAAAP//AQAuAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBC AAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAAA/wMA AAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIA FwAAADIMAABhAgAAAQAuagAAAAAA//8BAC4AjAABAAAAAACVAAEABAAAAAAAAACWAAEAAgAA AAkAjAABAAAAAAA= 8) 1; 2; 3; 5; 8;…

a n = 1 n + 1 ; a n = − n k ; a n = ( − 1 ) n + 1 ⋅ 1 5 , n ∈ N size 12{a rSub { size 8{n} } = { {1} over {n+1} } ;`a rSub { size 8{n} } = - { {n} over {k} } ;`a rSub { size 8{n} } = \( - 1 \) rSup { size 8{n+1} } cdot { {1} over {5} } ,``n in N} {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAATEdAADm AwAAAwEAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAADAdAADlAwAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlv biBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAACAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQAC AAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAABqAAAAYQIAAAEAYdMAAAAA AP//AQBhAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNl cmlmAAAAAAAAGQEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAAB AIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAD4BAADlAgAAAQBujQAAAAAA//8B AG4AjAABAAAAAACLAAEAAgAAAB8AigABADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACm AQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/ ////AIYAAQAEAAAAAAAAAHIAAgAaAAAA3AEAAGECAAABAAAAPQBPAQAAAAD//wEAPQCMAAEA AAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYB AAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP// //8AhgABAAQAAAAAAAAAcgACABcAAAByBAAAcgEAAAEAMdMAAAAAAP//AQAxAIwAAQAAAAAA iwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAAigABADwAAAADADYAAAAKAE9w ZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEA AgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQAAAATwMAANwBAABLBgAA8AEA AIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAA AAAApgEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAF AAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAGkDAACEAwAAAQBu0wAAAAAA//8BAG4AjAAB AAAAAACLAAEAAgAAAB8AigABADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8A AAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYA AQAEAAAAAAAAAHIAAgAaAAAAVwQAAIQDAAABAAAAKwD2AAAAAAD//wEAKwCMAAEAAAAAAIsA AQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMA AAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgAB AAQAAAAAAAAAcgACABcAAABgBQAAhAMAAAEAMdMAAAAAAP//AQAxAIwAAQAAAAAAiwABAAIA AAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUA AAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAA AAAAAAByAAIAFwAAAIMGAABhAgAAAQA7jQAAAAAA//8BADsAjAABAAAAAACLAAEAAgAAAB8A igABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAA AgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAA AHIAAgAXAAAApgcAAGECAAABAGHTAAAAAAD//wEAYQCMAAEAAAAAAIsAAQACAAAAHwCKAAEA QgAAAAMAPAAAABAATGliZXJhdGlvbiBTZXJpZgAAAAAAABkBAAAAAAMAAAAFAAAAAAACAP8D AAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgAC ABcAAAB6CAAA5QIAAAEAbo0AAAAAAP//AQBuAIwAAQAAAAAAiwABAAIAAAAfAIoAAQA8AAAA AwA2AAAACgBPcGVuU3ltYm9sAAAAAAAApgEAAP//AAAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/ AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAGgAAABgJAABh AgAAAQAAAD0ATwEAAAAA//8BAD0AjAABAAAAAACLAAEAAgAAAB8AigABADwAAAADADYAAAAK AE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACI AAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAaAAAAVgoAAGECAAABAAAA EiJPAQAAAAD//wEAEiKMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJh dGlvbiBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAACAP8DAAAAAAAAAAAA/wMAAAAAAIgA AQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADjCwAAcgEAAAEAbtMA AAAAAP//AQBuAIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGEAAEABQAAAAAAAAAA igABADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAA AAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAGcAAQAQ AAAArgsAANwBAAC4DAAA8AEAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABM aWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAA AAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAOMLAACEAwAA AQBruwAAAAAA//8BAGsAjAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVy YXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACI AAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAABg0AAGECAAABADuN AAAAAAD//wEAOwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlv biBTZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAACAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQAC AAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAAAODgAAYQIAAAEAYdMAAAAA AP//AQBhAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNl cmlmAAAAAAAAGQEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAAB AIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAPwOAADlAgAAAQBujQAAAAAA//8B AG4AjAABAAAAAACLAAEAAgAAAB8AigABADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACm AQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/ ////AIYAAQAEAAAAAAAAAHIAAgAaAAAAmw8AAGECAAABAAAAPQBPAQAAAAD//wEAPQCMAAEA AAAAAIsAAQACAAAAHwCKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAA AAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgAB AAQAAAAAAAAAcgACABoAAADZEAAAYQIAAAEAAAAoAI8AAAAAAP//AQAoAIwAAQAAAAAAiwAB AAIAAAAfAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9sAAAAAAAApgEAAP//AAAAAAUAAAAA AAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAA AAByAAIAGgAAAHcRAABhAgAAAQAAABIiTwEAAAAA//8BABIijAABAAAAAACLAAEAAgAAAB8A igABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAAAACmAQAAAAADAAAABQAAAAAA AAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAA AHIAAgAXAAAAzxIAAGECAAABADHTAAAAAAD//wEAMQCMAAEAAAAAAIsAAQACAAAAHwCKAAEA PAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAA AAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABoAAAC+ EwAAYQIAAAEAAAApAI8AAAAAAP//AQApAIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8 AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAAGQEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAA AAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAEIU AACnAQAAAQBujQAAAAAA//8BAG4AjAABAAAAAACLAAEAAgAAAB8AigABADwAAAADADYAAAAK AE9wZW5TeW1ib2wAAAAAAAAZAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACI AAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAaAAAA4RQAAKcBAAABAAAA KwCkAAAAAAD//wEAKwCMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJh dGlvbiBTZXJpZgAAAAAAABkBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgA AQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAACaFQAApwEAAAEAMY0A AAAAAP//AQAxAIwAAQAAAAAAiwABAAIAAAAfAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9s AAAAAAAApgEAAP//AAAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcA AQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAGgAAAOkVAABhAgAAAQAAAMUi9AAAAAAA//8B AMUijAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYA AAAAAACmAQAAAAADAAAABQAAAAAAAAD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwAB AAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA1xYAAHIBAAABADHTAAAAAAD//wEAMQCM AAEAAAAAAIsAAQACAAAAHwCFAAEABQAAAAAAAAABhAABAAUAAAAAAAAAAIoAAQA8AAAAAwA2 AAAACgBPcGVuU3ltYm9sAAAAAAAApgEAAP//AAAAAAUAAAAAAAAA/wMAAAAAAAAAAAD/AwAA AAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAABnAAEAEAAAAL0WAADcAQAA vxcAAPABAACMAAEAAAAAAIsAAQACAAAAHwCKAAEAQgAAAAMAPAAAABAATGliZXJhdGlvbiBT ZXJpZgAAAAAAAKYBAAAAAAMAAAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAA AQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADXFgAAhAMAAAEANdMAAAAAAP// AQA1AIwAAQAAAAAAiwABAAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlm AAAAAAAApgEAAAAAAwAAAAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcA AQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAABUYAABhAgAAAQAsagAAAAAA//8BACwA jAABAAAAAACLAAEAAgAAAB8AigABAEIAAAADADwAAAAQAExpYmVyYXRpb24gU2VyaWYAAAAA AACmAQAAAAADAAAABQAAAAAAAgD/AwAAAAAAAAAAAP8DAAAAAACIAAEAAgAAAAEAhwABAAUA AAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAHRkAAGECAAABAG7TAAAAAAD//wEAbgCMAAEA AAAAAIsAAQACAAAAHwCKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAA AAAFAAAAAAAAAP8DAAAAAAAAAAAA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgAB AAQAAAAAAAAAcgACABoAAAAMGgAAYQIAAAEAAAAIIi0BAAAAAP//AQAIIowAAQAAAAAAiwAB AAIAAAAfAIoAAQBCAAAAAwA8AAAAEABMaWJlcmF0aW9uIFNlcmlmAAAAAAAApgEAAAAAAwAA AAUAAAAAAAIA/wMAAAAAAAAAAAD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEA BAAAAAAAAAByAAIAFwAAAGMbAABhAgAAAQBOGQEAAAAA//8BAE4AjAABAAAAAACVAAEABAAA AAAAAACWAAEAAgAAAAkAjAABAAAAAAA=

Первая формула- для последовательности № 2, вторая - нет последовательности, третья - для последовательности № 4

Угадайте закономерность

1) а п =(п+1) 2 2) а п =п/(п+1) 3) а п =1/((п+1)(п+2)) 4) а п =(-1) п+1 /(п+1)

Способы задания последовательности на примерах

• Аналитический
• Рекуррентный
• Графический
• Словесный
• Табличный

Аналитический

формула n - го члена

Примеры:

1) а n = 2 n + 3 a 1 = 2 ·1 + 3 = 5 a 2 = 2·2 + 3 = 7 a 3 =2 ·3 + 3

2 ) а n = 100 - 10n 2 Найдите первые три члена.

3) a n = n 2 - 2n - 6 Является ли членом последовательности (-3)?

2) а 1 =90, а 2 =60, а 3 =40 3) а 3 =-3

Рекуррентный

Пример:

Дана последовательность:

а 1 = 1, а 2 = 3, а n +2 = 2а n + а n+1

а 3 = 2 а 1 + а 2 = 2 . 1 + 3 = 5

а 4 = 2 а 2 + а 3 = 2 . 3 + 5 = 11

а 5 = 2 а 3 + а 4 = 2 . 5 + 11 = 21 …

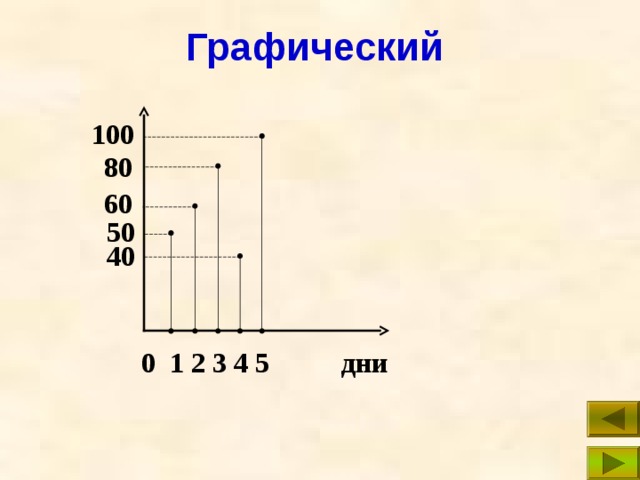
Графический

100

80

60

50

40

0 1 2 3 4 5 дни

Словесный

Пример:

3; 7; 13; 19; 29; …

Это - простые числа (через одно)

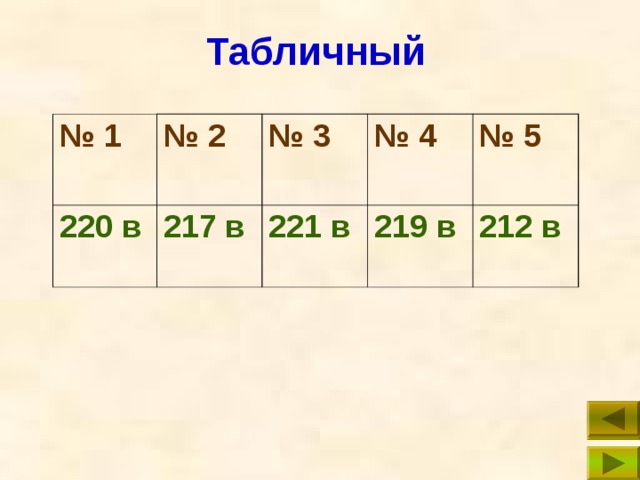
Табличный

№ 1

№ 2

220 в

№ 3

217 в

№ 4

221 в

№ 5

219 в

212 в

В классе

Домашнее

задание

• с. 3 6
• B № 177, 179-180,
• 183
• C № 186(1)
• П № 192-193
• по вариантам

• гл. 2, § 1
• № 175, 178,181, 182

Дом.задание может быть по учебнику, который используется в конкретном классе…