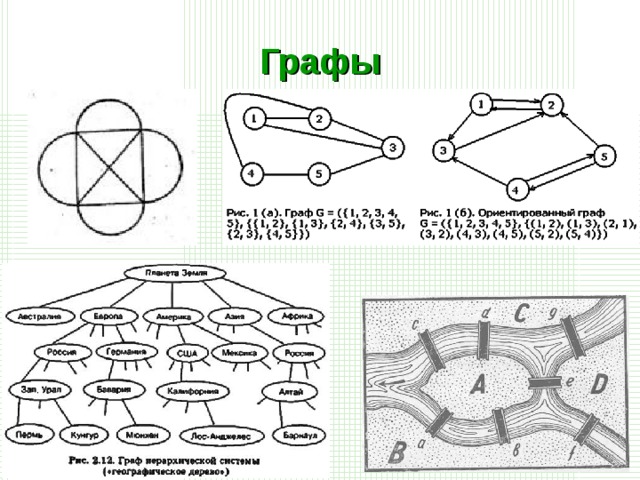
Слайд 1.
Актуальность. Графы один из интересных разделов математики. В школах графы часто используются на олимпиадах при решении нестандартных задач. Решение многих математических задач легче решаются, если удается использовать графы. Решение с помощью графов придает задачам наглядность и простоту.
Новизна. В работе рассмотрены уникурсальные звезды, приведено применение функции Эйлера при построении определенным способом таких звезд с любым количеcтвом вершин.
Слайд 2
Цель проекта. На основе изучения элементов теории графов рассмотреть и найти возможные формы и способы построения уникурсальных звезд.
Задачи проекта:
1. Изучить историю возникновения теории графов. Рассмотреть элементы теории графов.
2. Рассмотреть возможные формы и способы построения уникурсальных звезд с применением функции Эйлера.
3. Разработать алгоритм построения уникурсальных звезд.
Данный проект может быть использован при проведении математических кружков.
Слайд 3
Понятие уникурсальных фигур
Граф – это набор точек, некоторые из которых соединены линиями.
Леонард Эйлер (1707–1783) показал, что граф можно обойти, пройдя по каждому ребру только один раз.
Если фигуру можно нарисовать, не отрывая карандаша от бумаги и не проводя одну и ту же линию дважды, такая фигура называется уникурсальной. Уникурсальные пути в графе (не обязательно весь граф, может быть только его часть) называются Эйлеровыми путями.
Слайд 4.
Уникурсальные звезды
Мы займемся звездами – фигурами, полученными последовательным соединением точек, количеством более двух, расположенных в определенном порядке, например, на окружности.
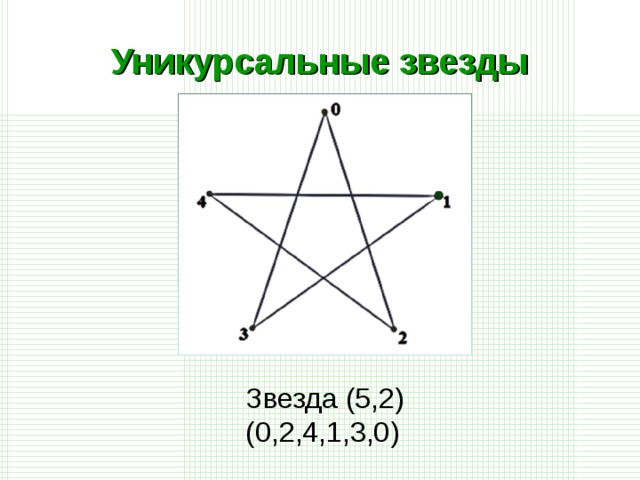
Простой пример – пятиконечная звезда.
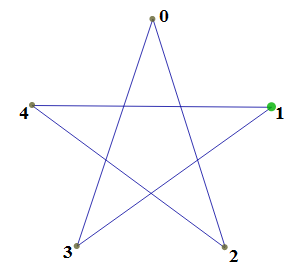 Рис.3
Рис.3
Так как форма звезды, очевидно, зависит от нумерации вершин, будем нумеровать вершины, начиная с нуля. Пятиконечная звезда имеет вершины 0, 1, 2, 3 и 4. При этом они соединены в определенном порядке. Порядок соединения определяет форму звезды. Пятиконечную звезду, изображенную на рисунке можно записать (0, 2, 4, 1, 3, 0). Начинать следует всегда с вершины 0. Номер вершины, следующей за нулевой, назовем шагом. В этих терминах звезда (0, 2, 4, 1, 3, 0) получает обозначение 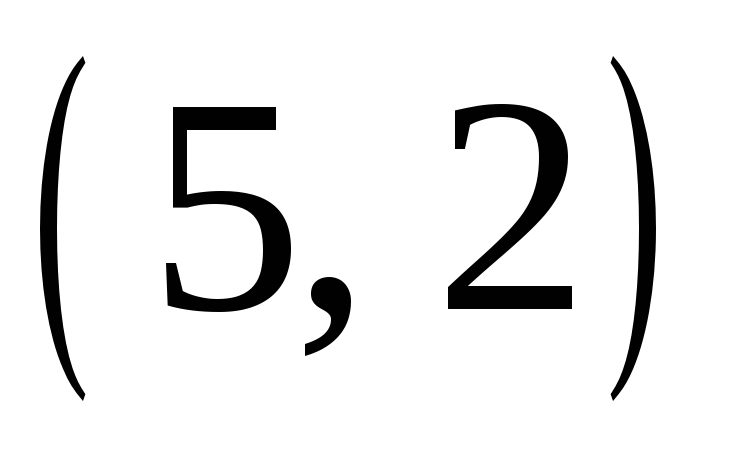 .
.
Если звезду с 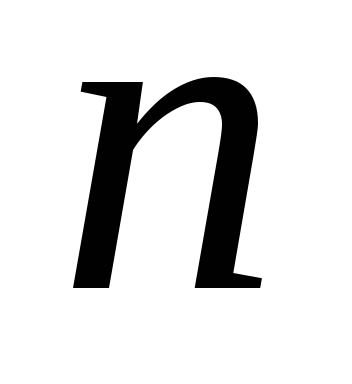 вершинами можно получить шагом
вершинами можно получить шагом 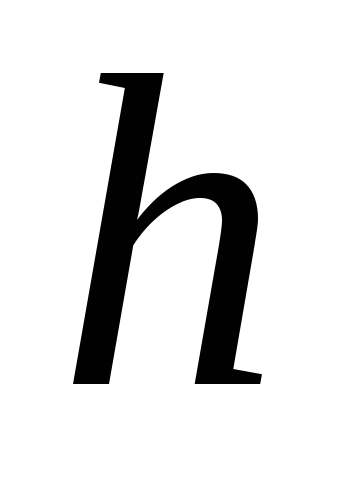 , то ее можно получить и с шагом
, то ее можно получить и с шагом 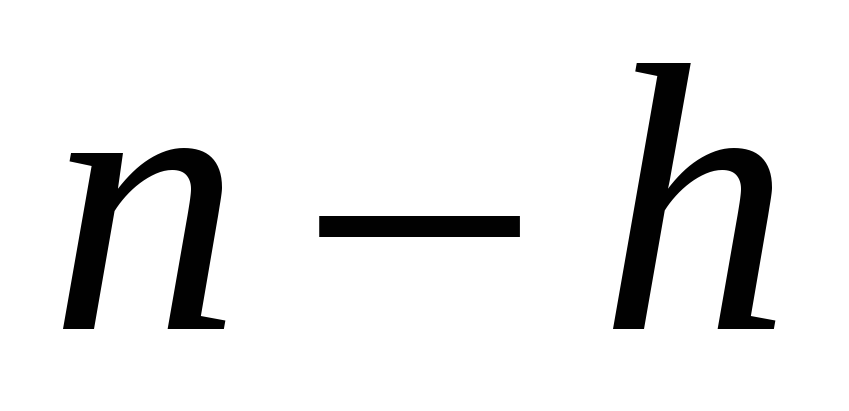 . Например, геометрически звезды
. Например, геометрически звезды 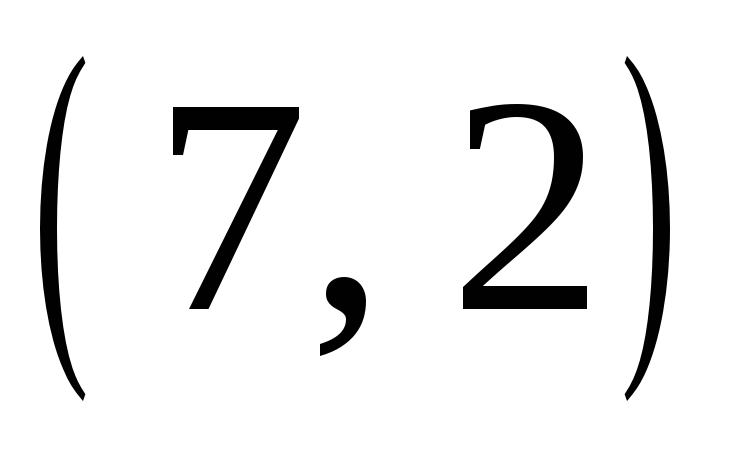 и
и 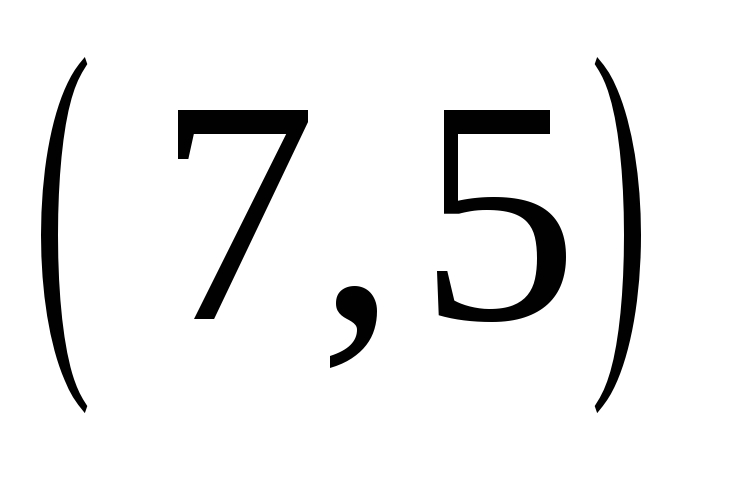 совпадают.
совпадают.
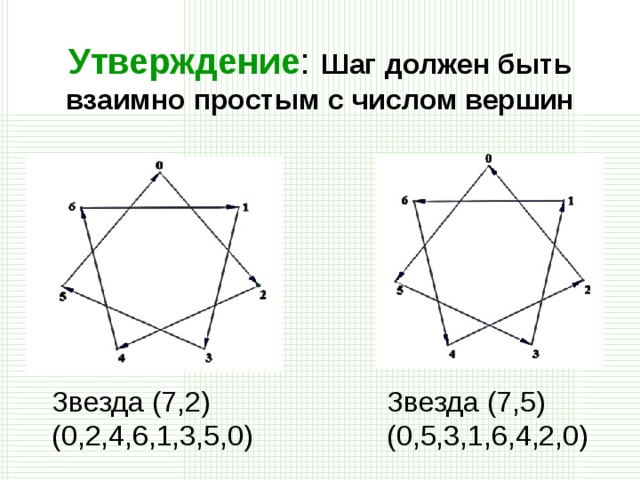
| 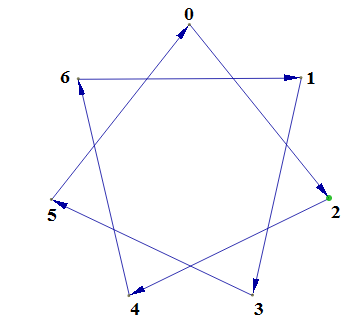 Рис. 4 Звезда 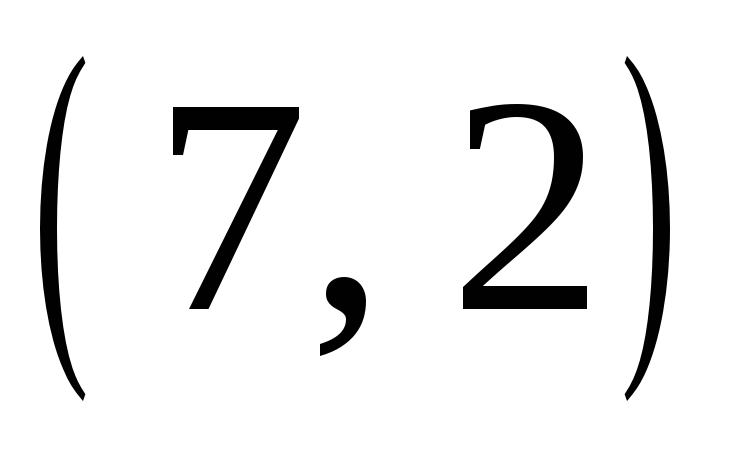 (0,2,4,6,1,3,5,0) | 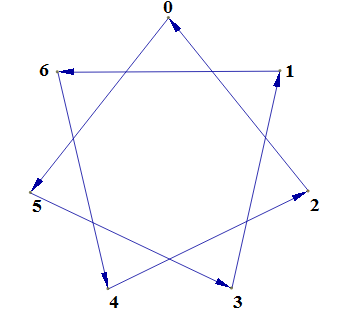 Рис. 5 Звезда 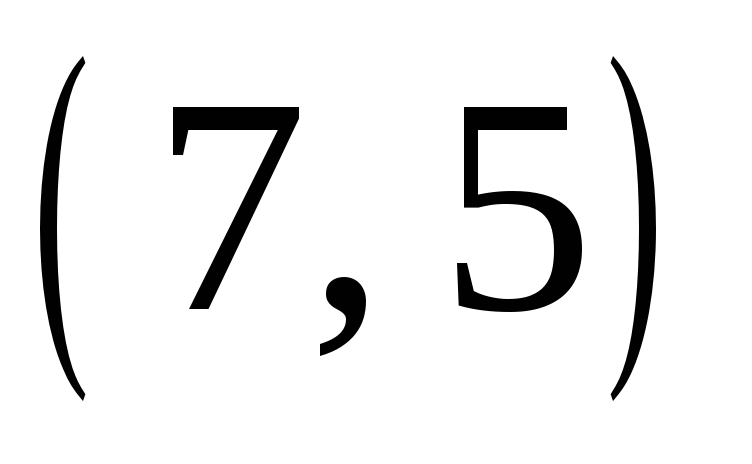 (0,5,3,1,6,4,2,0)
|
Поэтому в дальнейшем мы рассматриваем звезды только с шагом построения �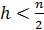 �.
�.
Слайд 5.
Утверждение 1. Шаг должен быть взаимно простым с числом вершин 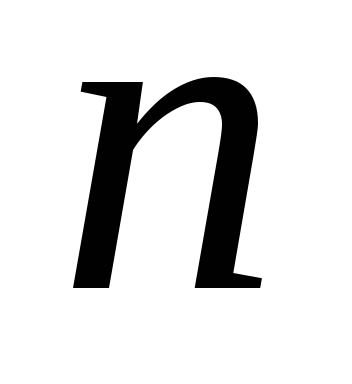 .
.
Слайд 6.
Пример 1. Для звезды с 6 вершинами существует единственная вырожденная форма 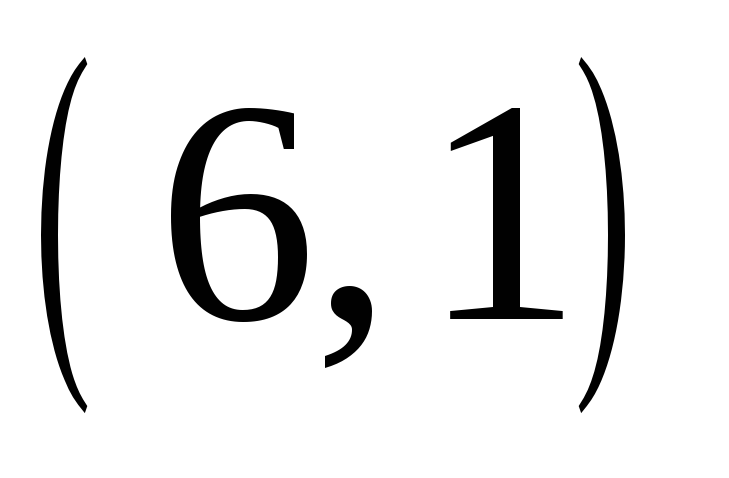 , поскольку числа 2 и 3 не могут быть шагами – они не взаимно просты с 6.
, поскольку числа 2 и 3 не могут быть шагами – они не взаимно просты с 6.
Пример 2. Для звезды с 8 вершинами имеются формы (8,1), (8,3), которые соответственно совпадают с (8,7) и (8,5). При этом нельзя построить звезды с (8,2), (8,4), (8,6).Отметим, что (8,6) совпадала бы с (8,2).
Слайд 7.
Функция Эйлера для подсчета количества форм звезд
Сколько существует различных звезд? Шаг построения h определяет одну звезду, значит, число различных звезд зависит от количества различных шагов. Наша задача определить такие шаги, тем самым найдя количество форм звезд. Для этих целей можно применить функцию Эйлера, так как шаг должен быть взаимно простым с числом вершин 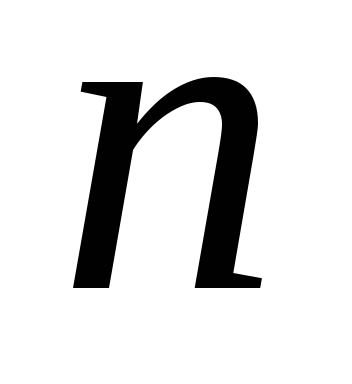 .
.
Рассмотрим множество целых чисел, взаимно простых с n и не превосходящих n. Количество этих чисел обозначается φ(n) и называется функцией Эйлера.
Функция Эйлера 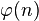 определяет количество натуральных чисел, меньших
определяет количество натуральных чисел, меньших 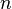 и взаимно простых с ним и принимает вид:
и взаимно простых с ним и принимает вид:
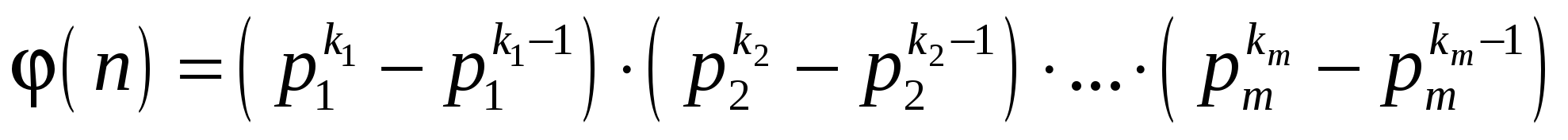 , где
, где 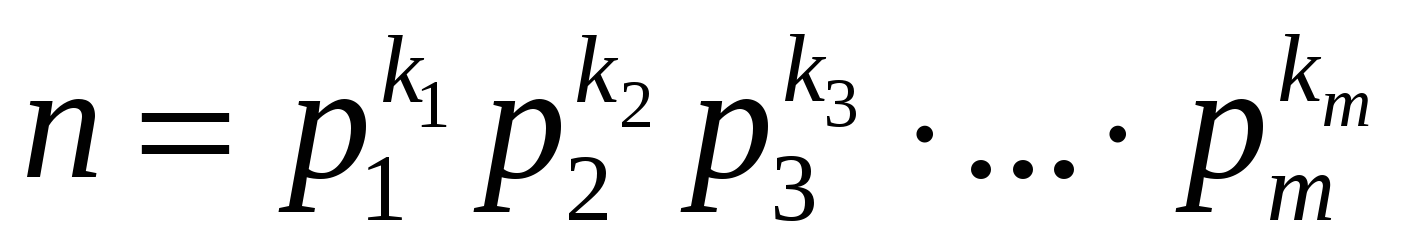 .
.
При этом полагают, что число 1 взаимно просто со всеми натуральными числами и 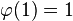 .
.
Слайд 8.
Если количество вершин 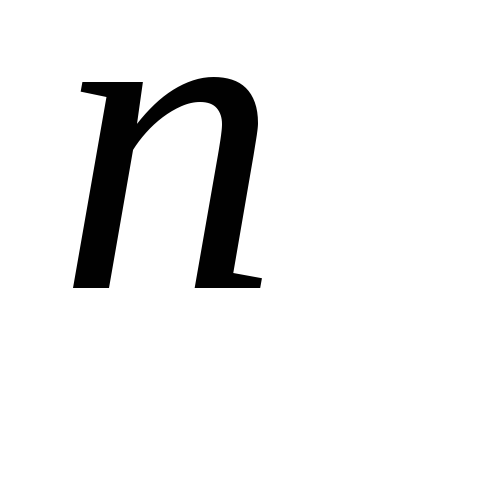 - составное число, то его можно разложить на простые в соответствии с основной теоремой арифметики:
- составное число, то его можно разложить на простые в соответствии с основной теоремой арифметики:
Общий ответ: всего существует 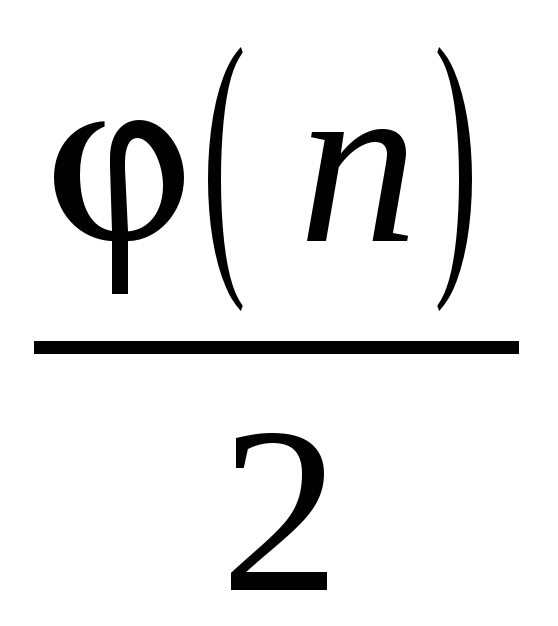 звезд с
звезд с 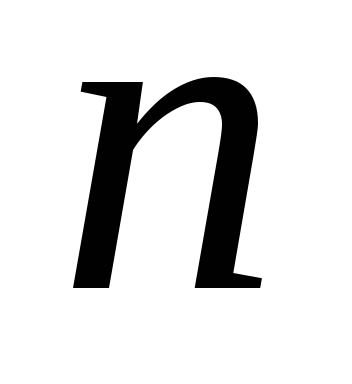 вершинами.
вершинами.
Если количество вершин простое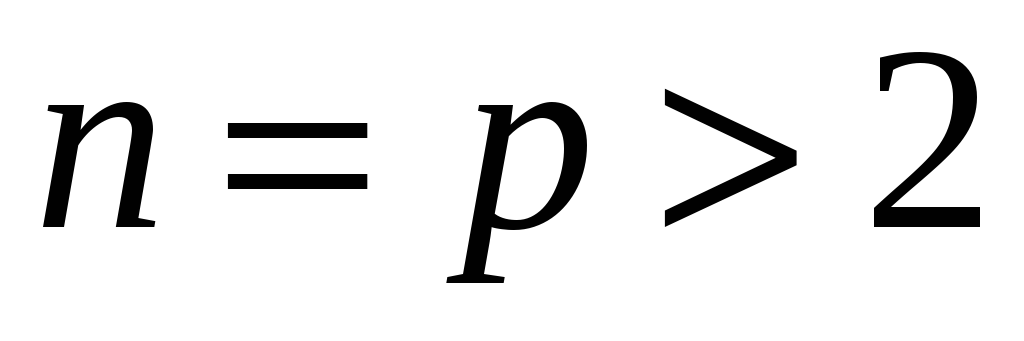 , то
, то
существует ровно 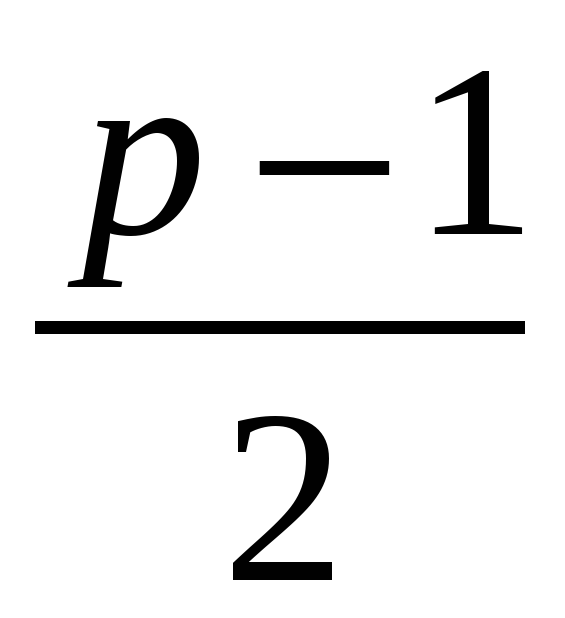 геометрически различных звезд (форм такой звезды).
геометрически различных звезд (форм такой звезды).
Слайд 9.
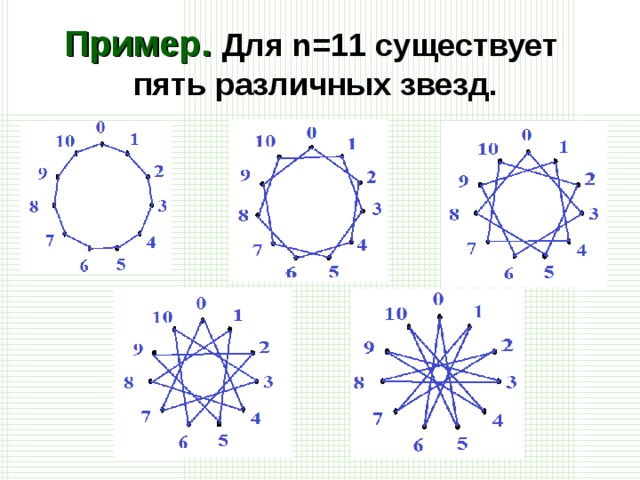
Пример. Для 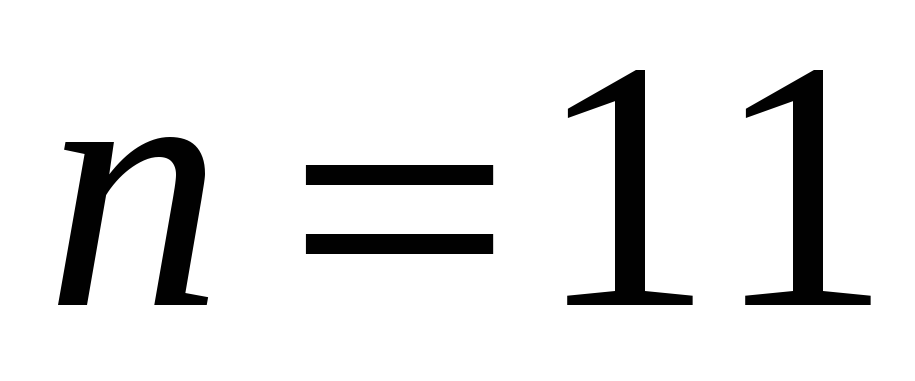 существует �
существует �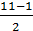 �=5 пять различных звезд.
�=5 пять различных звезд.
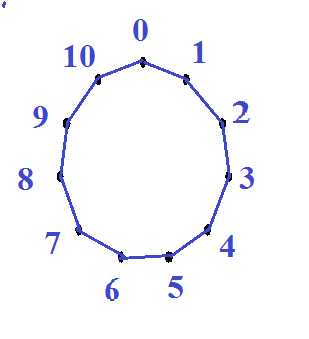
| 
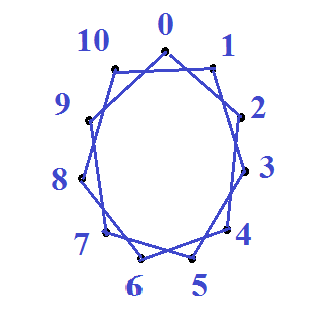
| 
|
| Рис.6 Звезда (11,1) | Рис.7 Звезда (11,2) |
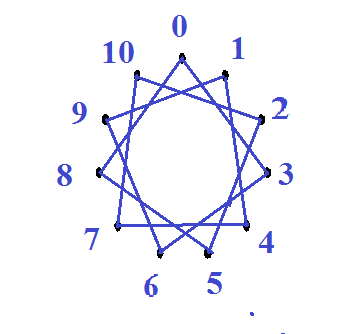
| 
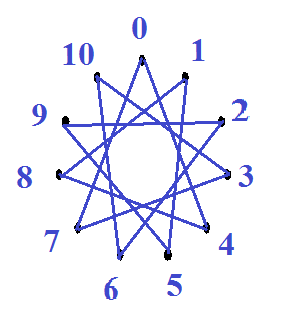
| 
|
| Рис.8 Звезда (11,3) | Рис.9 Звезда (11,4) |
| 
|
| Рис.10 Звезда (11,5) |
Слайд 10.
Алгоритм построения
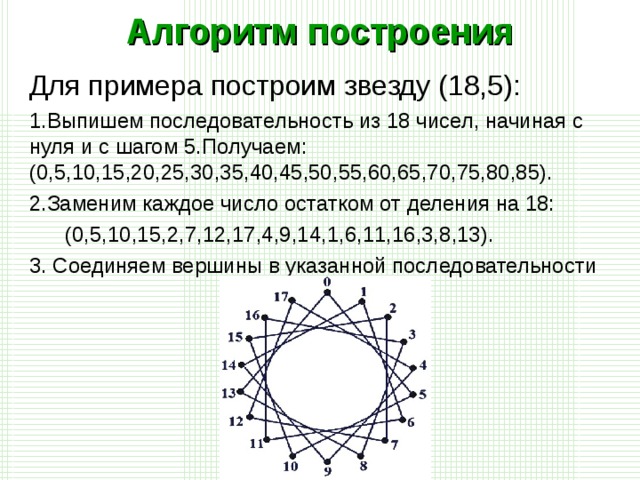
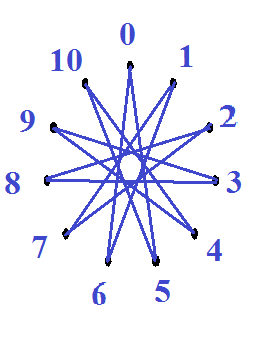
Для примера построим звезду 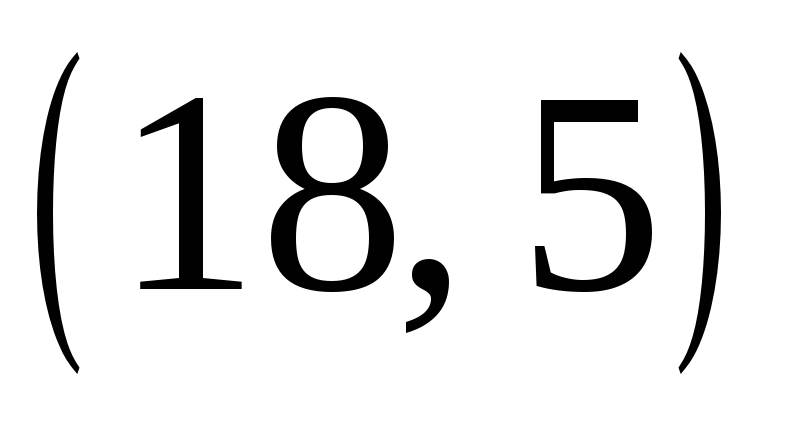 .
.
Выпишем последовательность из 18 чисел, начиная с нуля и с шагом 5. Получаем: 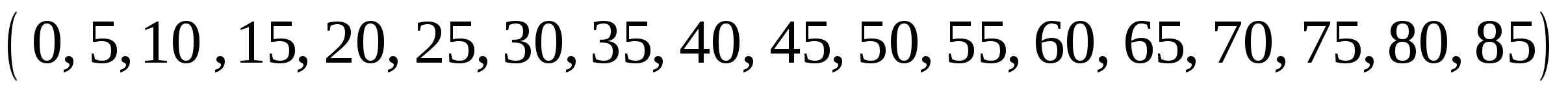 .
.
Заменим каждое число остатком от деления на 18:
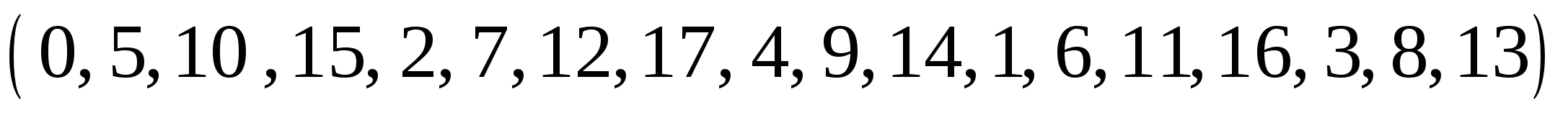 .
.
Получаем последовательность. Соединяем вершины в указанной последовательности
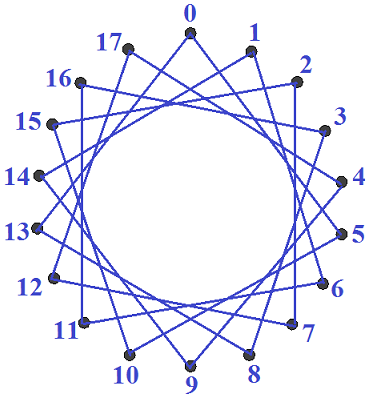
Рис.11
Слайд 11.
Применение уникурсальных звезд в жизни и творчестве
При исследовании уникурсальных звезд нами было замечено, что технология создания уникурсальных звезд применяется при вышивке – изонить.
Слайд 12.
ЗАКЛЮЧЕНИЕ
«Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал, что чувство удивления – могучий источник желания знать: от удивления к знаниям – один шаг». А математика замечательный предмет для удивления.
Именно это мы попытались показать в своей работе, исследуя свойство уникурсальных звезд.
В ходе выполнения данного проекта получены следующие результаты:
1.Рассмотрены элементы теории графов.
2. Приведено применение функции Эйлера при построении.
3. Разработан алгоритм построения уникурсальных звезд.
Слайд 13.
Cписок используемой литературы
Дмитриев И.Г., Алексеева Г.И., Баишева М.И. Олимпиады по математике города Якутска 1995-2001 – Якутск: ИРО, 2002.
Кордемский Б.А. Математическая смекалка – М.: Просвещение, 2000.
Панюкова Т.А. Комбинаторика и теория графов. – М.: Книжный дом «ЛИБРОКОМ», 2012.-208 с.
http://ru.wikipedia.org
http://mccme.ru
http://olimpiada.ru





 Рис.3
Рис.3