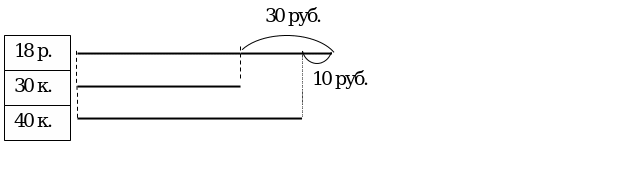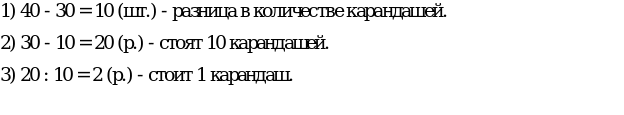Дайджест "Педагогический практикум по решению текстовых задач"

Материалы работы городской творческой группы учителей начальных классов

Педагогический практикум по решению текстовых задач

Составитель:

руководитель творческой группы

С.В.Черношей

учитель начальных классов

МБОУ СОШ мкр.Вынгапуровский

г.Ноябрьск

2019-2020 уч.г.

СОДЕРЖАНИЕ

1.Актуальность создания творческой группы ………………………………...3

2. 1 I этап. Восприятие и семантический анализ задачи………………...……4

2.2. II этап. Моделирование……………………………………...……………...7

2.3. III этап. Поиск и составление плана решения задачи……………………10

2.4 IV этап. Запись решения и ответа задачи…………………………………16

2.5. Vэтап. Проверка решения задачи………………………………………... 16

2.6 VI этап. Исследовательская работа над задачей ………...……………….18

3. Дополнительные виды работы над задачей ………………. ……………... 21

4. Приёмы работы с уже решенной задачей…………………………………. 28

5. Исследовательская работа над уже решенной задачей…………………... 33

6. Нестандартные задачи и их виды………………………………………….. 38

7.Методы решения нестандартных задач…………………………………….. 41

8.Нестандартная задача как компонент начального математического образования……………………………………………………………………... 50

9.Приемы работы с комбинаторными задачами………………………………59

10. Приемы работы по решению логических задач и задач на установление соответствия между элементами различных множеств………………………64

11. Список литературы…………………………………………………….……70

АКТУАЛЬНОСТЬ

создания творческой группы

Важнейшим приоритетом начального общего образования в настоящее время является формирование общеучебных умений, навыков и способов познавательной деятельности, уровень освоения которых в значительной мере предопределяет успешность обучения на последующих этапах образования.

Согласно стандартам нового поколения, выпускник начальной школы должен владеть обобщёнными способами решения учебных задач, его необходимо научить осмысленно обрабатывать информацию, анализировать её, выявлять главное, «ядро» информации, устанавливать взаимосвязи между понятиями, проводить классификацию, сравнивать, делать обобщения. Это мыслительные операции, которые включает в себя словесно – логическое мышление. Этот тип мышления должен стать доминирующим к концу начальной школы.

Мышление человека, главным образом, состоит из постановки и решения задач. Особенно большую роль играют задачи в обучении математике. В них заложены большие возможности для повышения общего и математического образования учащихся, развития смекалки, начал исследовательской работы, логического мышления.

В начальной школе решаются, главным образом, сюжетные, текстовые задачи. Они являются моделями количественной стороны жизненных явлений. Решению таких задач уделяется большое внимание при обучении младших школьников

Зачастую при обучении учащихся решению задач основное внимание направлено на реализацию единственной цели – получение ответа на вопрос задачи, «натаскивание» учащихся на решение тех или иных видов задач.

Глобальной проблемой до сих пор является неумение учащихся решать задачи, находить разные способы решения, действовать в нестандартных ситуациях, например, при выполнении тестовых работ, приобретающих с каждым годом всё большую популярность. Этой проблеме были посвящены работы мною уважаемых авторов Н. Б. Истоминой и С. Е. Царёвой, которые, на мой взгляд, положили начало нестандартному подходу к работе над задачей в начальной школе. Замечательные тетради Н. Б. Истоминой «Учимся решать задачи»* помогают эффективно решать данные проблемы. Многие современные учебники по математике (особенно учебники Л. Г. Петерсон*) тоже содержат большое количество упражнений, направленных на формирование общеучебных умений, а именно:

1) выполнять семантический и математический анализ текстовых задач

(представлять ситуацию, описанную в тексте задачи, выделять данные и искомые величины, устанавливать взаимосвязи между ними);

2) представлять выявленные взаимосвязи в виде схематических и символических моделей (переводить словесную модель в символическую);

3) составлять план решения задачи посредством рассуждений;

4) проверять решение задачи;

5) проводить исследовательскую работу над задачей.

Формирование вышеперечисленных умений осуществляется, благодаря использованию различных эффективных приёмов и методов, специфичных для каждого этапа работы над задачей, а также применению разнообразных нетрадиционных видов работы с текстовыми задачами.

Но, к сожалению, учителя начальной школы часто отказываются от нетрадиционных методов работы над задачей в силу трудоёмкости и ограниченности во времени в рамках 45-минутного урока. Во главу угла ставится количество решённых задач, а не качество работы, что влечёт за собой поверхностное отношение к текстам задач, действия по образцу, неумение выполнять задания с нестандартными формулировками.

Как же научить учащихся не действовать по шаблону, а творчески, с интересом подходить к процессу решения задач? Для этого существует большое количество замечательных приёмов, упражнений, которые действительно дают высокие результаты. Школьники начинают любить решать задачи, этот процесс становится для них не скучным, трудоёмким занятием, а «вкусным», занимательным, требующим работы мысли.

Учитель начальных классов Вынгапуровской МБОУ СОШ, Силенок Е.Н.

I ЭТАП

ВОСПРИЯТИЕ И АНАЛИЗ ЗАДАЧИ

Цель этапа: понять задачу, представить, о чём эта задача; установить, что известно, что нужно найти, как связаны между собой данные и искомое.

Одной из главных причин, по которым школьники неверно решают ту или иную задачу

является неспособность глубоко, осмысленно, внимательно проанализировать то, что дано

задаче (данные) и то, что нужно узнать (вопрос), и взаимосвязи между ними. Мы постоянно

напоминаем детям: «Внимательно читайте условие и вопрос». Но ошибки продолжают

существовать. Чтобы решить эту проблему, я использую в работе следующие приёмы:

Первый подэтап:

1) Чтение текста задачи: сначала про себя, затем вслух одним из учеников.

2) Пересказ задачи своими словами (этот приём способствует более глубокому осмыслению прочитанного).

3) Представление жизненной ситуации, описанной в задаче, инсценировка этой ситуации.

Второй подэтап (графическая работа с цветом):

4) Разбиение текста задачи на смысловые части, подчёркивание условия и вопроса синим и красным цветом, выделение числовых данных.

5) Выделение наиболее важных слов в каждой смысловой части и в вопросе задачи.

Вот как должен выглядеть текст задачи после этого подэтапа:

«Лена нарисовала 10 шариков./ 3 шарика она раскрасила красным цветом/, синим – на 2 шарика больше /, остальные шарики – зелёным цветом. / Сколько зелёных шариков на рисунке у Лены? (Синим цветом выделяем условие, красным – вопрос).

Третий подэтап:

6) Переформулировка текста задачи (отбрасывание несущественных деталей, зачёркивание).

Этот приём целесообразно использовать, если текст задачи объёмный и

содержит много несущественных деталей.

«В саду было 5 кустов облепихи. Когда посадили ещё несколько, то в саду стало 9 кустов облепихи. Сколько кустов посадили?»

«Было 5 кустов облепихи. Стало 9 кустов. Сколько кустов посадили?»

7) Переконструирование текста задачи (У –В – У, В – У – У У – В )

В учебниках чаще всего используются задачи типичной конструкции У – В, это способствует развитию у учащихся стереотипов, автоматизма при анализе текста задачи. Важно, как можно чаще использовать тексты нетипичных конструкций: текст задачи состоит из одного сложного вопросительного или повествовательного предложения, в котором стоит сначала вопрос, потом условие; часть условия представлена в начале текста, потом следует вопрос и другая часть условия; вместо слова «сколько

» в вопросе используются слова «найди», «узнай» и т. д.).

«Около школы росло 20 тополей. Сколько тополей посадили осенью, если стало 43 тополя?» (У – В – У)

«Сколько кроликов было в клетке, если после того, как отсадили 7 cерых кроликов, осталось 5 белых кроликов?» (В – У – У)

«Узнай массу яйца кукушки, если оно на 1 грамм меньше яйца стрижа, которое весит 4 грамма»

Дополнительно для обучения учащихся анализировать текст задачи можно использовать следующие упражнения:

1) Анализ текстов задач с лишними и недостающими данными.

«На дереве сидело 8 птичек. Сначала улетели 3 птички, потом ещё 2. Сколько птичек улетело?»

«На одном проводе сидели ласточки, а на другом – 7 воробьёв. Сколько всего сидело птиц на проводах?»

2) Анализ текстов задач с противоречивым условием.

«На одной клумбе растёт 10 хризантем, а на другой – 15. Сколько тюльпанов на двух клумбах?»

3) Анализ текстов задач с вопросом, в котором спрашивается о том, что уже известно.

«На клумбе росло 5 тюльпанов и 3 розы. Сколько тюльпанов росло на клумбе?»

4) Анализ текстов задач с неопределённым условием.

« В вазе лежало 3 яблока, 5 апельсинов, а груш на 2 меньше. Сколько всего фруктов в вазе?» (не указано, с чем сравнивается количество груш).

5) Сравнение текстов задач (сравниваются задачи, сходные по сюжету, но разные по математическому содержанию, либо с одинаковым математическим содержанием, но совершенно разных по сюжету).

«В вазе лежало 3 яблока, а апельсинов на 2 больше. Сколько апельсинов лежало в вазе?»

«В вазе лежало 3 яблока, их на 2 больше, чем апельсинов. Сколько апельсинов лежало в вазе?»

6) Составление условия к данному вопросу.

Составь условие к данному вопросу.

«Сколько марок в двух конвертах?»

«Сколько зебр привезли в зоопарк?»

7) Постановка вопроса к данному условию.

Поставь вопрос к данному условию.

«В Тихом океане 9 морей, а в Атлантическом на 3 моря меньше».

«В Тихом океане 9 морей, а в Индийском океане 5 морей».

8) Подбор условия к данному вопросу или вопроса к данному условию.

Подбери условие к данному вопросу.

«Сколько кленовых листьев засушила Таня?»

а) Осенью Таня засушила 4 кленовых и 5 дубовых листьев.

б) Осенью Таня засушила 9 листьев. Из них 4 дубовых.

в ) Осенью Таня засушила 5 кленовых листьев, а дубовых на 4 больше.

г) Осенью Таня засушила 9 дубовых листьев, а кленовых на 4 меньше.

Подбери вопрос к данному условию.

«Дикие гуси живут 80 лет, а собаки 20 лет».

а) Сколько всего лет живут гуси и собаки?

б) На сколько лет гуси живут больше, чем собаки?

в) На сколько лет гуси живут меньше, чем собаки?

г) Сколько лет живут гуси?

Учитель начальных классов школы №6,

Наволенко Галина Яковлевна

I I этап - МОДЕЛИРОВАНИЕ

Моделирование - это замена действий с реальными предметами действиями с уменьшенными образцами, моделями, с их графическими заменителями: рисунками, схемами, чертежами, таблицами. Модель должна помочь ученику понять содержание задачи, выявить отношения между данными и искомым, найти разные способы решения задачи, увидеть новые,

не отражённые в задаче отношения.

Для того, чтобы самостоятельно решать задачи, школьнику нужно освоить различные виды моделей, научиться выбирать модель, соответствующую предложенной задаче и переходить от одной модели к другой. Наша задача – научить школьников применять тот способ моделирования, который наиболее подходит к той или иной задаче, помогает увидеть отношения между данными и искомым, найти разные способы решения задачи (если это возможно), увидеть скрытые взаимосвязи, не отражённые явно в тексте задачи.

На мой взгляд, самой удачной, с этой точки зрения, моделью, является схематический чертёж и менее удачной – краткая запись опорными словами. Правильно выполненный чертёж наиболее точно отражает все взаимосвязи, о которых идёт речь в задаче. Но, к сожалению, не к каждой задаче подходит эта модель. Обычно, после анализа задачи, я предлагаю учащимся самим выбрать подходящую модель, учу находить их «плюсы» и «минусы» той или иной модели.

Для формирования умения моделировать задачу, я использую следующие приёмы:

1) Составление краткой записи задачи при помощи опорных слов (рисунка, схемы, таблицы и т. д.). Этот приём чаще всего используется на уроках в начальной школе.

2) Выбор рисунка, схемы и т. д. к данной задаче.

Выбери схему, подходящую к данной задаче.

«В течение жизни человек спит 25 лет. 5 лет их них он видит сны. Сколько лет в течение жизни человек спит и не видит снов?»

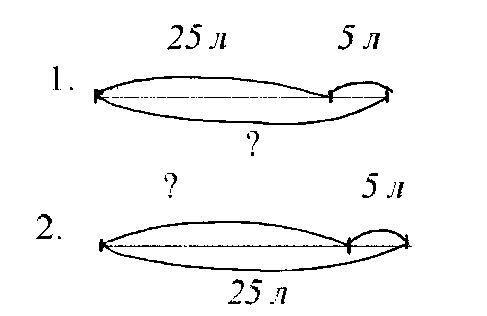
3) Исправление ошибок в краткой записи задачи.

Соответствует ли данная схема задаче? Исправь ошибки в схеме, если они есть.

« В сосновом бору поселились 5 уссурийских тигров, их было на 2 меньше, чем в кедровом лесу. Сколько тигров поселилось в кедровом лесу?»

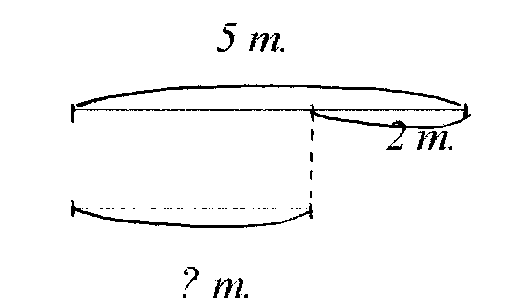
4) Составление задачи по краткой записи (опорным словам, рисунку, схеме, чертежу, таблице).

Составь задачу по схеме.

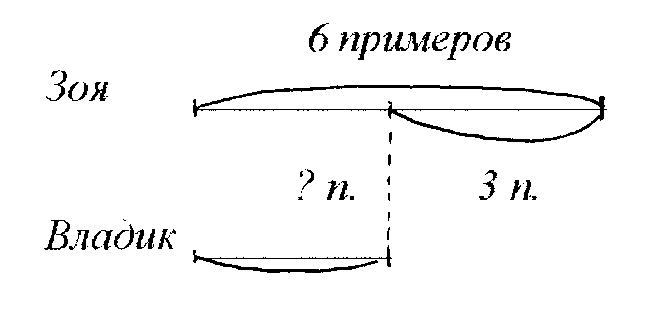
5) Подбор к схеме подходящего текста из предложенных.

Подбери к схеме соответствующий текст задачи.

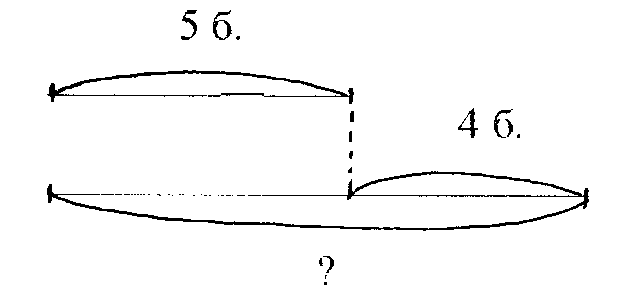
а) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек адмиралов – на 4 больше. Сколько адмиралов участвовало в конкурсе?

б) В конкурсе красоты приняли участие 9 бабочек адмиралов, а махаонов на 4 меньше. Сколько махаонов участвовало в конкурсе?

в) В конкурсе красоты приняли участие 5 бабочек махаонов, а бабочек адмиралов на 4 больше. Сколько всего бабочек приняли участие в конкурсе?

г) В конкурсе красоты приняли участие 5 бабочек махаонов, это на 4 меньше, чем бабочек адмиралов. Сколько адмиралов приняло участие в конкурсе?

д) В конкурсе красоты приняли участие 5 бабочек махаонов и 9 бабочек адмиралов. На сколько больше адмиралов приняли участие в конкурсе?

6) Установление взаимноодназначного соответствия – проведение «дорожек» от слова к его изображению на схеме.

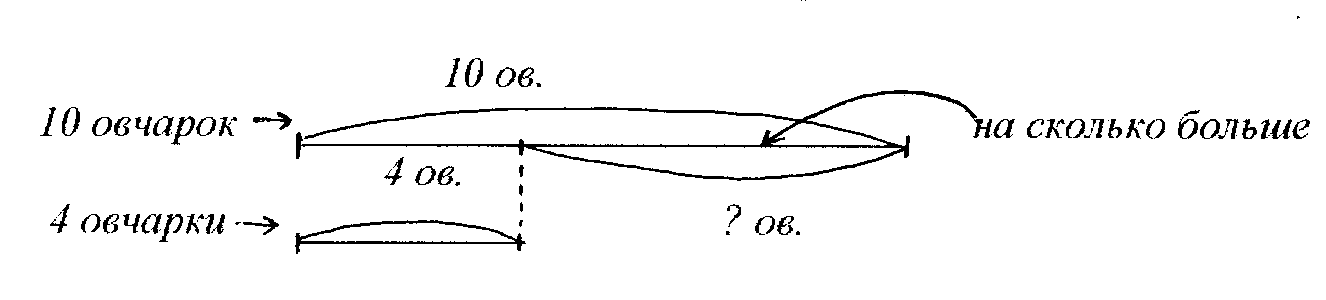
Объясни данную схематическую модель в соответствии с текстом задачи.

«В собачью школу ходят 10 немецких овчарок и 4 шотландских овчарки. На сколько больше немецких овчарок ходит в собачью школу?»

III ЭТАП

ПОИСК И СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ ЗАДАЧИ

Учитель начальных классов Вынгапуровской МБОУ СОШ, Терещук Валентина Васильевна

Самым важным на этом этапе является формирование умения рассуждать тем или иным способом. Поиск плана решения задачи можно проводить двумя путями:

- аналитическим способом, рассуждая от вопроса к данным ( «Чтобы ответить на вопрос задачи, надо знать … и … );

- синтетическим, рассуждая от данных к вопросу.(«Мне известно … и …. По этим данным я могу узнать… и …).

Возможно использование их комбинации – аналитико-синтетического способа.

Чаще всего применяется аналитический способ рассуждения, но с точки зрения психологии в 1-2 классе ребёнку легче освоить синтетический способ разбора, так как в возрасте 6-8 лет формирование у ребёнка способности к синтезу несколько опережает формирование способности к анализу. На своих уроках я стараюсь использовать и аналитический, и синтетический способы разбора. Поиск и составление плана решения учащимися начинается с самостоятельного обдумывания, обсуждения в парах, группах, составления цепочек рассуждений.

1) Разбор от вопроса к данным ( аналитический способ)

Поиск плана решения данным способом начинается с вопроса задачи. Выясняется, что нужно узнать, чтобы ответить на вопрос задачи. Для этого необходимо найти какую-то величину. А что нужно знать, чтобы её найти? и т. д.

Чтобы помочь учащимся вести рассуждения аналитическим способом, можно использовать приём «ДЕРЕВО РАССУЖДЕНИЙ». Суть его заключается в том, что по ходу рассуждений строится схема, которая помогает учащимся увидеть, какие простые задачи следует выделить (если это задача составная), и каким будет план решения данной задачи.

1. «В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7 ?»

- На какой вопрос нужно ответить?

- Что нужно знать, чтобы ответить на вопрос задачи? (нужно знать, сколько зебр было и сколько зебр стало).

- Известно ли в задаче, сколько зебр было? ( известно: было 2 зебры).

- Известно ли, сколько зебр стало? (известно: стало 7 зебр).

- Как узнать, сколько привезли зебр? На сколько больше стало зебр? ( на 5)

- Значит, сколько привезли зебр? (5)

- Каким действием решим задачу, почему?

?

было стало

7 5

2. «В зоопарке 5 обезьян, слонов на 3 меньше, а бизонов столько, сколько слонов и обезьян вместе. Сколько бизонов в зоопарке?»

- На какой вопрос нужно ответить?

- Что сказано о бизонах в тексте задачи?

- Что нужно знать, чтобы ответить на вопрос задачи? ( сколько обезьян и слонов вместе)

- Можем ли мы узнать, сколько обезьян и слонов вместе? (нет, не знаем, сколько слонов).

- Что сказано в тексте о слонах? ( слонов на 3 меньше, чем обезьян). Что значит на 3 меньше?

- Как узнать, сколько слонов? Почему выбрали действие вычитания?

- Теперь, можем ответить на вопрос задачи? Каким действием? Почему выбрали действие сложения?

?

обезьяны слоны

5 + ?

обезьяны – 3

- Какие простые задачи можно выделить в данной составной?

«ДЕРЕВО РАССУЖДЕНИЙ» ОТ ВОПРОСА К ДАННЫМ

?

?

знаю не знаю

?

знаю не знаю

знаю знаю

Можно оформить рассуждения в таблице. Учитель выдаёт заготовки таблицы, в которые учащиеся записывают свои рассуждения. Такую работу целесообразно периодически проводить в 3, 4 классе.

Чтобы узнать	Надо знать
сколько бизонов	сколько обезьян (5)
	сколько слонов (?)
сколько слонов	сколько обезьян (5)
	на сколько слонов меньше, чем обезьян (на 3)

2. Разбор от данных к вопросу (синтетический)

Синтетический способ характеризуется тем, что основным, направляющим вопросом при поиске плана решения задачи является вопрос о том, что можно найти по двум или нескольким известным в задаче числовым значениям (данным). По вновь полученным числовым данным и другим известным в задаче данным вновь ищется ответ на вопрос, что можно узнать по этим значениям. И так до ответа на вопрос задачи. Суть этого способа состоит в выделении учащимися простой задачи из составной и решении её.

« В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало 9».

- Что известно в задаче? ( сколько было зебр и сколько стало).

- Что можно узнать по этим данным? ( на сколько больше стало зебр)

- Как узнать, на сколько больше стало зебр?( от 9 нужно отнять 2)

- Почему зебр стало больше? (привезли несколько зебр)

- Сколько зебр привезли?

2 9

было стало

привезли

?

«В зоопарке 5 обезьян, слонов на 3 меньше, чем обезьян, а бизонов столько, сколько обезьян и слонов вместе. Сколько бизонов в зоопарке?»

- Что известно в задаче? ( сколько обезьян;, на сколько слонов меньше, чем обезьян).

- Что можно узнать по этим данным? (сколько слонов). Какую задачу можно составить и решить?

- Как узнать, сколько слонов? ( от 5 отнять 3).

- Почему выбрали действие вычитания?

- Какие данные имеем теперь? (знаем, сколько обезьян и сколько слонов).

- Что можно узнать по этим данным? (сколько обезьян и слонов вместе).Какую задачу можно составить по этим данным?

- Как узнать, сколько слонов и обезьян вместе, каким действием? Почему сложением?

- Что сказано о бизонах? Сколько бизонов в зоопарке?

1. 3

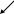5 ? слонов

?

всего

Можно использовать таблицу.

Зная	Узнаем
сколько обезьян (5)	сколько слонов ( -)
на сколько слонов меньше, чем обезьян (3)
сколько обезьян	сколько слонов и обезьян вместе ( +) сколько бизонов
сколько слонов

«ДЕРЕВО РАССУЖДЕНИЙ» ОТ ДАННЫХ К ВОПРОСУ

знаю знаю

?

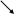
могу знаю

узнать

?

могу

узнать

Для формирования умения выделять простые задачи из составной, вести рассуждения от данных можно использовать следующие упражнения:

1) Составь и реши простые задачи, используя эти данные.

« С одной пасеки собрали 12 кг мёда, а с другой 9 кг. Весь мёд разлили в бидоне по 7 кг в каждый»

2) Поставь вопрос к данному условию. Выбери только те простые задачи, которые помогут ответить на главный вопрос.

«В школьный буфет привезли 5 ящиков яблок по 10 кг в каждом, и 4 ящика апельсинов, по 8 кг в каждом»

а) В школьный буфет привезли 5 ящиков яблок и 4 ящика апельсинов.

Сколько всего ящиков фруктов привезли в буфет?

б) В школьный буфет привезли 5 ящиков яблок по 10 кг в каждом.. Сколько кг яблок привезли?

в) В школьный буфет привезли 4 ящика апельсинов по 8 кг в каждом. Сколько кг апельсинов привезли?

г) В школьный буфет привезли5 ящиков яблок и 4 ящика апельсинов. На сколько больше привезли ящиков с яблоками, чем ящиков с апельсинами?

д) В каждом ящике с яблоками 10 кг, а в ящике с апельсинами 8 кг. На сколько

больше в каждом ящике кг яблок, чем апельсинов?

Материалом для таких упражнений могут служить любые составные задачи, представленные в учебнике, если использовать только условия этих задач.

3) Использование аналогии при поиске плана решения

В основе этого способа лежит сравнение задач, при котором выявляется полное или частичное сходство отношений между данными величинами в условии ранее решённой задачи и вновь предложенной и высказывается предположение, что для решения новой задачи можно воспользоваться планом ранее решённой задачи.

1) «Два мальчика выбежали одновременно навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скоростью 4 м /с. С какой скоростью бежал второй мальчик?

План решения задачи:

І способ.

1.Найти путь, который пробежал первый мальчик до встречи.

2. Найти путь, который пробежал второй мальчик до встречи.

3. Найти скорость, с которой бежал второй мальчик.

II способ.

1. Найти скорость сближения.

2. Найти скорость, с которой бежал второй мальчик до встречи.

2) «Из города к зимовке, расстояние между которыми 150 км, выехали аэросани со скоростью 60 км /ч. В это же время навстречу им из зимовки вышел лыжник и встретил аэросани через 2 часа. Найти скорость лыжника»

Сходства: 1. Движение двух предметов навстречу друг другу;

2. Одновременное начало движения;

3. Известно расстояние между пунктами, скорость одного предмета и время до встречи;

4. Требуется найти скорость второго предмета.

ВЫВОД: Можно использовать план решения первой задачи.

4) Поиск плана решения по модели

В некоторых случаях графическая модель подсказывает план решения задачи.

« С одного поля собрали 370 т зерна, а с другого – в два раза больше. Сколько тонн зерна собрали с двух полей?»

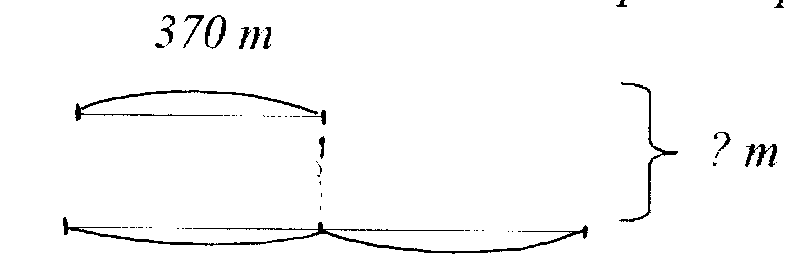
Данная модель показывает, для того, чтобы узнать общее количество зерна, нужно взять 3 раза по 370 тонн.

Решение задачи: 370 * 3 = 1110 (т)

5) Поиск плана решения путём составления уравнения

«С первого участка собрали 98 кг картофеля, со второго – 104 кг. Сколько кг картофеля собрали с третьего участка, если всего собрали 270 кг картофеля?»

- Что требуется узнать в задаче?

х кг – собрали картофеля с третьего участка

- Какие числовые данные известны в задаче?

98 кг – собрали с первого участка

104 кг – собрали со второго участка

270 кг – собрали всего с трёх участков

______________________________________

Схема уравнения: I + ІІ + III = всего

98 + 104 + х = 270

202 + х = 270

х = 68

IV ЭТАП

ЗАПИСЬ РЕШЕНИЯ И ОТВЕТА

Учитель начальных классов

школы №7, Арсланова

Наталья Александровна

Запись решения и ответа может производиться различными способами:

1 класс – выражением в одно действие или по действиям с пояснениями (составная задача);

2 класс - по действиям с пояснениями или вопросами;

3 класс – по действиями с пояснениями или вопросами, а также в виде числового или буквенного выражения;

4 класс – все способы + уравнением.

Мои ученики, начиная с 3-го класса, решают каждую задачу по действиям с пояснениями или вопросами и обязательно составляют выражение. Таким образом, формирование умения записывать решение задачи с помощью выражения является более эффективным.

V ЭТАП

ПРОВЕРКА РЕШЕНИЯ

Этот этап играет большую роль в развитии самоконтроля, формировании умения рассуждать, внимательно относиться к анализу задачи, активизирует познавательную деятельность. Зачастую, учащиеся получают ответ, который не может получиться с точки зрения здравого смысла. Но, если они не научены решение проверять, но такой результат их не удивляет.

После анализа задачи и составления плана решения, мы выполняем прикидку ответа, то есть устанавливаем границы значений искомого с точки зрения здравого смысла.

После того, как задача решена, можно составить обратные задачи или решить задачу другими способами, если это возможно, и сравнить полученные результаты.

Мой любимый приём - «подстановка данных», в текст задачи вставляются полученные числа и устанавливается соответствие между ними и данными числами.

Для проверки решения задач используются следующие приёмы:

1. Прикидка ответа или установление границ значений искомого с точки зрения здравого смысла (до решения).

В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7?»

- Если в зоопарке было 2 зебры, а стало 7 зебр, может получиться в ответе число большее 7? Обоснуйте свой ответ.

1. Установление соответствия между числами, полученными в результате решения задачи, и числами, данными в условии (приём подстановки).

В зоопарке было 2 зебры. Привезли ещё несколько зебр. Сколько зебр привезли, если их стало в зоопарке 7?»

7 – 2 = 5 (з.)

- Было 2 зебры, привезли 5 зебр. Стало 7 зебр.

2 + 5 = 7 (з.)

- Сравните число, полученное при проверке с данным в задаче.

При проверке простой задачи этот способ совпадает со способом составления и решения обратной задачи. В 1 классе (1-4) используется данный способ, понятие «обратная задача» не вводится.

1. Составление и решение обратных задач.

Этот способ вводится во 2 классе (1-4).

Составить обратную задачу – это значит преобразовать данную задачу так, чтобы искомое данной задачи стало данным числом, а одно из данных чисел – искомым.

Например:

« Портниха купила 10 м ткани на костюм и платье. На платье она израсходовала 2м. Сколько метров ткани пошло на костюм, если у неё осталось 3 м?»

Обратные задачи:

1) «Портниха купила 10 м ткани на костюм и платье. На костюм она израсходовала 5 м. Сколько метров ткани пошло на платье, если у неё осталось 3 м?»

2) «Портниха купила 10 м ткани на костюм и платье. Сколько метров ткани у неё осталось, если на костюм она израсходовала 5 м ткани, а на платье 2 м?»

3) «Портниха израсходовала на костюм 5 м ткани и на платье2 м ткани. Сколько метров ткани купила портниха, если у неё осталось 3 м?»

1. Решение задачи другим способом (если это возможно в составной задаче).

Сравнение полученных результатов при решении задачи разными способами.

Например:

«На велогонках стартовало 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором -6. Сколько спортсменов пришло к финишу?»

I способ.

1. 70 – 4 = 66 (с.)- осталось после первого этапа

2. 66 – 6 = 60 (с.)

II способ.

1. 4 + 6 = 10 (с) – сошли с трассы на первом и втором этапах

2. 70 – 10 = 60 (с.)

Учитель начальных

классов школы №7

Довнар Ирина Дмитриевна

VI ЭТАП

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА НАД ЗАДАЧЕЙ

На мой взгляд, этот этап является очень важным и интересным, хотя зачастую он опускается. Именно работа над задачей на данном этапе способствует развитию творческой активности и мышления учащихся, повышает интерес к математике, к решению задач, позволяет целенаправленнее формировать компоненты общего умения решать задачи.

Приёмы работы над задачей на данном этапе:

Эти приёмы также способствуют развитию умения производить анализ задачи, устанавливать взаимосвязи между величинами, осознанно выбирать действие при решении задач.

1) Решение задачи другим способом (если это возможно), сравнение разных способов решения;

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м.

3 часть площади занята цветами, а остальная часть – овощами и ягодами.

Чему равна площадь участка, занятая овощами и ягодами?»

1 способ

1) 120 * 85 = 10200 (кв.м ) – S участка

2) 10200 : 3 = 3400 (кв.м ) – занято цветами

3) 10200 – 3400 = 6800 (кв.м )

2 способ

1) 120 * 85 = 10200 (кв.м) – S участка

2) 120 : 3 = 40 (м) – длина участка, занятого цветами

3) 40 * 85 = 3400 (кв.м) – Sучастка, занятого цветами

4) 10200 – 3400 = 6800 (кв.м )

3 способ

1) 120 : 3 = 40 (м) – длина участка, занятого цветами

2) 120 – 40 = 80 (м) – длина участка, занятого овощами и ягодами

3) 85 * 80 = 6800 (кв. м)

4 способ

1) 120 : 3 = 40 (м) – длина участка, занятого цветами

2) 40 * 85 = 3400 (кв. м) – S участка, занятого цветами

3) 3400 * 2 = 6800 (кв. м)

5 способ

1) 120 * 85 = 10200 (кв.м) – S участка

2) 10200 : 3 = 3400 (кв.м) – S участка, занятого цветами

3) 3400 * 2 = 6800 (кв. м)

6 способ

1) 120 : 3 = 40 (м) – длина участк5а, занятого цветами

2) 40 * 2 = длина участка, занятого овощами и ягодами

3) 80 * 85 = 6800 (кв. м)

2) Составление аналогичной задачи с новыми данными.

Этот приём помогает детям переносить известную схему решения на другие задачи этого вида, учит обобщать их в группы.

3) Постановка дополнительных вопросов к решённой задаче.

Этот приём предполагает постановку дополнительных вопросов, замену известных величин неизвестными, поиск новых решений.

«Два лыжника вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 66 км. Скорость первого -12 км/ч, второго – 10 км/ч. Через какое время они встретятся?»

Что ещё можно узнать по имеющимся в тексте задачи и полученным данным? (На сколько скорость первого лыжника больше скорости второго лыжника? Сколько км прошёл до встречи первый лыжник? Сколько км прошёл до встречи второй лыжник? На сколько км больше прошёл до встречи первый лыжник? На каком расстоянии друг от друга будут лыжники через 1 час после встречи, через 2 часа после встречи? и т. д. )

4) Изменение вопроса задачи.

- Измени вопрос так, чтобы задача решалась в одно действие, в два действия.

- Измени вопрос так, чтобы задача решалась вычитанием (делением, …).

Этот приём позволяет решить несколько задач по одному и тому же условию (при решении составных задач), тем самым экономя время, которое тратится на осмысление условия.

Например:

«В первый день улитка проползла 5 м, во второй на 2 м больше. Сколько метров проползла улитка во второй день?»

Измени вопрос задачи так, чтобы задача решалась в два действия.

5) Изменение условия задачи так, чтобы задача решалась другим действием.

6) Изменение числовых данных задачи так, чтобы появился новый способ решения.

7) Исследование решения.

Сколько способов решения имеет задача? При каких условиях она не имела бы решения? Какие приёмы целесообразны для поиска решения задачи?

8) Сравнение задач и их решения. Этот приём позволяет глубже осознать взаимосвязи между величинами, входящими в задачу, способствует лучшему усвоению идеи решения, формированию осознанного подхода к анализу задачи, выбору действий. Дети определяют, что одно и то же слово, один и тот же вопрос не определяют выбор действия и, что для этого нужно установить связи между величинами и на их основе выбрать, а затем выполнить действие.

Сравнение задач вырабатывает у учащихся привычку не начинать поиск решения задачи без глубокого, полного анализа задачи.

Кроме основного вида работы над задачей – её решения, можно использовать и другие виды работы, не включающие явное и полное решение задач, но способствующие формированию комплекса умений, необходимых для плодотворного решения задач, развитию мышления, творческой активности, познавательного интереса.

Учитель начальных классов Вынгапуровской МБОУ СОШ, Теплых Галина Анатольевна

ДОПОЛНИТЕЛЬНЫЕ ВИДЫ РАБОТЫ НАД ЗАДАЧЕЙ

Математика — это предмет, на котором открываются большие возможности для развития способностей к познавательной деятельности. Особенность уроков математики в начальной школе заключается в том, что они строятся на системе задач и практических работ. Это значит, что многие новые понятия усваиваются при решении текстовых задач. Задачи выполняют очень важную функцию в начальном курсе математики — они являются полезным средством развития у детей логического мышления, умения проводить анализ и синтез, обобщать, абстрагировать и конкретизировать, раскрывать связи, существующие между рассматриваемыми явлениями. Решение задач - упражнения, развивающие мышление. Нельзя забывать, что работа над задачами воспитывает у детей многие положительные качества характера. Способствует воспитанию терпения, настойчивости, воли, пробуждению интереса к самому процессу поиска решения, даёт возможность испытать глубокое удовлетворение, связанное с удачным решением. Главная сила математики состоит в том, что вместе с решением одной конкретной задачи она создаёт общие приёмы и способы, применимые во многих ситуациях, которые даже не всегда можно предвидеть. 

«Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдётся путь!» (Д. Пойа)

Реестры затруднений по итогам мониторинговых исследований и Всероссийских проверочных работ показывают, что решение задач остаётся самым большим затруднением наших учащихся. Некоторые ученики даже не приступают к решению задач, испытывают страх. Чтобы помочь ученику, учителю необходимо применять различные приёмы решения текстовых задач. Тогда ученик выберет свой удобный и понятный ему приём. Вспомним некоторые приёмы решения текстовых задач, которые вы все, конечно, знаете и, уверена, применяете в своей практике.

На этапе ознакомления с содержанием текста задачи применяются такие приемы как:

Разбиение текста на смысловые части.

Цель: обеспечить порционную подачу материала, который содержится в задаче, что даёт возможность осмыслить, понять задачу.

Разбиение текста зависит от сложности задачи.

При разборе на части простой задачи, выделяют части, описывающие начало события; действие, которое произвели с объектом; конечный момент события (обычно задаётся в вопросе).

В основе разбора составной задачи лежит выделение простых задач.

Переформулировка текста задачи.

Цель приема – удалить несущественные детали, уточнить и раскрыть смысл существенных элементов.

Произвести замену одной ситуации на другую, более явно выраженную.

Например, решение задачи: «В магазин привезли 90 кг огурцов. К концу дня их осталось 20 кг. Сколько килограммов огурцов продали?»

• удобнее решать, если текст её будет сформулирован так:«Было 90 кг огурцов. Осталось 20 кг огурцов. Сколько килограммов огурцов продали?»

Чаще всего переформулировка используется при решении задач с пропорциональными величинами.

Дополнение условия.

• Произвести дополнение с учётом количественных характеристик.

Из бочки взяли 10 ведер воды. Сколько вёдер воды осталось в бочке?

Дополним задачу.

В бочке 40 вёдер воды. Из неё взяли 10 вёдер. Сколько вёдер воды осталось в бочке?

В первой задаче – если из бочки взяли 10 ведер, то надо понимать, что в ней было больше 10 ведер.

Во второй задаче – если в бочке было 40 ведер, то надо понимать, что можно взять меньше 40.

Выбор условия к данному вопросу.

• дан вопрос и несколько условий задачи, дети выбирают нужное условие. Учитель даёт верные и неверные условия.

Вопрос: Сколько детей занимается в студии?

Условия:

• В студии мальчики и девочки. Мальчиков на 7 меньше, чем девочек.

• В студии 20 девочек, а мальчиков на 7 меньше, чем девочек.

• В студии 20 девочек.

Выбор вопроса к данному условию.

Даётся условие задачи: Возле дома 7 яблонь, 3 вишни и 2 берёзы.

Выбери вопрос к задаче из нескольких предложенных.

• На сколько больше яблонь, чем вишен?

• Сколько ёлок возле дома?

• Сколько всего деревьев возле дома?

• На какие вопросы можно ответить, пользуясь данным условием? (на 1 и 3)

• На какие вопросы можно ответить, выполнив арифметические действия (учитель говорит арифметические действия, дети предлагают вопросы).

• Какой вопрос можно поставить к данному условию, так чтобы получилась задача? (Третий)

Выбор вопроса, для ответа на который нужно использовать все математические данные этого текста.

• Нацеливает на более сложную мыслительную операцию.

Задача: В школьном конкурсе чтецов участвовали по 2 человека из восьми классов. Половина участников стали победителями. Среди победителей 3 девочки.

- Какой вопрос мы выберем, если для ответа на него нужно использовать все математические данные из текста задачи? (Третий).

• Сколько учеников участвовали в конкурсе?

• Сколько учеников стали победителями?

• Сколько победителей мальчиков?

Соединение условия и вопроса.

Даётся несколько условий задач и несколько вопросов. Нужно соединить подходящие условия и вопросы, чтобы получились задачи. Сколько мыслительных операций нужно проделать, чтобы выполнить задание.

Выбор текстов по данному решению.

• Выбери задачу к решению: (4+5)+4=13 (фруктов)

• Маша купила 4 яблока и 5 груш. Сколько фруктов купила Маша?

• Маша купила 4 яблока, а груш на 5 больше. Сколько фруктов купила Маша?

• После чтения задачи дети выбирают текст задачи, который подходит к данному решению. Затем они объясняют причины ошибок.

.Составление задачи по данному решению.

• Составить задачу, которая решалась бы при помощи выражения:

( 12+18) : 5

Восстановление условия задачи.

• Восстанови условие задачи по её решению.

• У Пети было __ рублей. Он купил кисточку за ___ рублей и блокнот за ___ рублей. Сколько денег осталось у Пети?

48-(10+12)=26(руб.)

Путём размышления и рассуждения дети восстанавливают задачу и вставляют пропущенные числа. Обращают внимание на то, что невозможно вставить числа, например, так: Было 10 рублей. Купил кисточку за 48 рублей и блокнот за 12 рублей.

Выделение лишнего данного. Данного, которое не понадобится для решения задачи, которое нужно исключить.

• В новом пятиэтажном доме 2 подъезда. Дом должны были построить за 18 месяцев, а построили на 4 месяца быстрее. Больше или меньше года потребуется на строительство дома?

- Какие данные исключим из 1 задачи? (Подчёркнуто).

• Рите купили учебник по информатике и тетрадь к нему. За всю покупку заплатили 300 руб. Тетрадь, в которой 80 страниц, стоит 100 руб. Сколько стоит учебник?

- Что исключаем? (Подчёркнуто).

.На этапе поиска решения задачи применяются такие приемы как:

Обозначение или называние числовых данных.

Выбери и подчеркни, что обозначает каждое числовое данное в задаче.

• Мама купила 3 ручки. (Цена. Количество. Стоимость). Одна ручка стоит 5 рублей. (Цена. Количество. Стоимость).Сколько денег заплатила мама? (Цена. Количество. Стоимость)

• Лыжник прошёл дистанцию за 2 часа. (Скорость. Время. Расстояние.) В час он проходил 8км. (Скорость. Время. Расстояние.)Сколько километров прошёл лыжник? (Скорость. Время. Расстояние.)

Дополнение решения.

• Допиши действия, пропущенные в решении задачи и ответ.

• Велосипедист ехал из посёлка в город 3 часа со скоростью 16 км/ч. Обратно он поехал другой дорогой, которая была длиннее первой на 12 км, а скорость велосипедиста на обратном пути была на 4 км/ч меньше. Сколько времени потратил велосипедист на обратную дорогу?

1) 16 ∙ 3=48(км)

2) (48+12=60 (км)

3) 16 - 4=12(км/ч)

4) 60:12=5(ч)

Ответ: 5 часов.

Выбор решения по условию задачи.

После чтения задачи дети выбирают решение, которое подходит к данному тексту. Затем они объясняют причины ошибок неверных решений. В данной задаче они выполняют решение выражением. Выясняют, почему не подходит 2 и 3 решение?

• У Миши 81 рубль, а у Коли денег в 9 раз меньше. На все деньги мальчики купили видеокассету. Какова её цена?

а) (81:9)+81

б) (81:9)+9

в) 81+(81-9)

.Выбор решения по условию задачи.

• Выбери верное решение задачи. Для верного решения запиши пояснения к действиям.

• Клён сбрасывает ежегодно 30 кг листвы, дуб на 10 кг больше, чем клён, берёза на 5 кг меньше, чем клён. Сколько кг листьев они сбросят вместе?

1. 30+10=40(кг)-

2. 40-5=35(кг)-

3. 30+40+35=105(кг)-

Ответ: 105 килограммов

1. 30+10=40(кг)-

2. 30-5=25(кг)-

3. 30+40+25=95(кг)-

Ответ: 95 килограммов.

- Записывая пояснения, выясняют, что подходит второе решение, так как берёза – на 5 кг меньше, чем клён, а не дуб.

Комментирование выражений по условию задачи.

Постановка вопроса к каждому решению.

• На какой вопрос ответишь, выполнив действие:

• Юра и Вера одновременно побежали наперегонки. Юра пробежала 54 м, а Вера – 46 м.

54 + 46 54 – 46

• На какой вопрос ответишь, выполнив действие:

• В мастерской семь двухколёсных и три трёхколёсных велосипеда.

2·7 3·3 2·7+3·3 2+2+2+2+2+2+2+3+3+3

Заполнение недостающих данных

• Установление условий, при которых задача имеет или не имеет решение, имеет одно или несколько решений, а также установление условий изменения значения одной величины в зависимости от изменения другой.

• Подобрать числа и решить задачу.

Например: В нашем доме 60 жильцов, а в соседнем на 20 человек меньше. Сколько жильцов в соседнем доме?

• Каким действием будете решать задачу? (Вычитанием.)

• Что надо учитывать при подборе первого числа? (Возможное количество жильцов. Если числа поменяем местами, то задача не будет иметь смысла.)

• Что надо учитывать при подборе второго числа? (Оно должно быть меньше первого.

• Может ли второе число равняться 60? (Нет.Тогда получится, что во втором доме жильцов нет.)

• Может ли второе число быть больше 60? Например, равняться 70? (Нет, так как нельзя 60 уменьшить на 70.)

Работа по плану

Можно использовать разные приемы:

• решить задачу по составленному плану;

Работа по плану.

Продолжить составление начатого плана решения.

Работа по плану.

Самостоятельно составить план решения задачи.

Чем отличаются задания мониторинга? Многие текстовые задачи включают в себя логические рассуждения.

Поэтому вспомним некоторые приёмы решения логических задач.

Приём решения задачи табличным способом.

Переход от текстовой формы представления информации к табличной помогает решать достаточно трудные задачи.

Задача: Три подружки – Вера, Оля и Таня пошли в лес по ягоды. Для сбора ягод у них были корзинка, лукошко, ведёрко. Известно, что Оля была не с корзинкой и не с лукошком. Вера не с лукошком. Что с собой взяла каждая из девочек?

Давайте вместе решим задачу. Каков ответ? (на слайде 25)

Решение задачи

	Вера	Оля	Таня
корзинка	+	-
лукошко	-	-	+
ведёрко	-	+

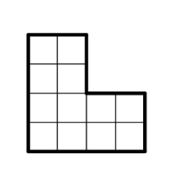
Приём на разрезания и распиливания.

Разрезать фигуру на 4 равные части. Попробуем сделать это вместе. Получилось?

Приём «Перебор вариантов»

В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.

Запишите варианты и посчитайте количество вариантов.

Ответ:
Вариант1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант6: 1) Громов, 2) Иванов, 3) Орлов.

Математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научив детей владеть умением решения задачи, мы окажем существенное влияние на развитие их мышления, на привитие интереса к предмету.

Учителю необходимо попробовать все приёмы для решения задач, так как этот вид работы традиционно остаётся самым трудным и самым важным в курсе «Математика».«Умение решать задачи – такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путём подражания или упражнения». «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их». (Д.Пойа)

Учитель начальных классов МБОУ СОШ мкр.Вынгапуровский Бобровникова Светлана Викторовна

Приемы работы с уже решенной задачей

1) Блиц-турниры. Блиц-турнир предполагает устное решение простых и составных задач с числами и с переменными (обобщённый вариант) за определённый отрезок времени, запись только решения задачи.

2) Составление выражений, необходимых для решения задач с неопределёнными данными.

«От двух пристаней, находящихся на расстоянии км, отплыли

Одновременно навстречу друг другу катер и моторная лодка. Встреча

произошла через часов. Катер шёл со скоростью км/ч. С какой

скоростью шла моторная лодка?»

1 способ.

1) ∙ - расстояние, пройденное катером

2) - ∙ - расстояние, пройденное моторной лодкой

3) ( - ∙ ) : - скорость моторной лодки

2 способ.

1) : - скорость сближения

2) : - - скорость моторной лодки

3) Составление устного плана решения ( «Дерево рассуждений») и его объяснение без последующих вычислений.

4) Разъяснение готового плана решения задачи (вопросы, «Дерево рассуждений»)

5) Пояснение готовых способов решения задачи.

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м.

3 часть площади занята цветами, а остальная часть – овощами и ягодами.

Чему равна площадь участка, занятая овощами и ягодами?»

1 способ: 4 способ:

1) 120 * 85 = 10200 (кв.м ) – …… 1) 120 : 3 = 40 (м) - …….

2) 10200 : 3 = 3400 (кв.м ) - ……. 2) 40 * 86 = 3400 (кв.м ) - ……..

3) 10200 – 3400 = 6800 (кв.м ) - ……. 3) 3400 * 2 = 6800 (кв.м ) -

2 способ: 5 способ:

1) 120 * 85 = 10200 (кв.м ) - …….. 1) 120 * 85 = 10200 (кв.м ) -

2) 120 : 3 = 40 (м) - ………. 2) 10200 : 3 = 3400 (кв.м ) -

4) 10200 – 3400 = 6800 (кв.м ) - ………

3 способ: 6 способ:

1) 120 : 3 = 40 (м) - ……… 1) 120 : 3 = 40 (м) - ……..

2) 120 – 40 = 80 (м) - ……. 2) 40 * 2 = 80 (м) - ……..

3) 85 * 80 = 6800 (кв.м ) - …… 3) 80 * 85 = 6800 (кв.м ) -

6) Составление решения задачи разными способами в соответствии с данными пояснениями.

«От двух пристаней, находящихся на расстоянии 510 км, отплыли

Одновременно навстречу друг другу катер и моторная лодка. Встреча

произошла через 15 часов. Катер шёл со скоростью 19 км/ч. С какой

скоростью шла моторная лодка?»

1способ.

1)…………. - прошёл катер до встречи

2) ………………… - проплыла моторная лодка до встречи

3) ………………… - скорость моторной лодки

2 способ.

1) …………………. - скорость сближения

2) …………………..- скорость моторной лодки

7) Соотнесение пояснения с решением.

Усложнённый вариант – соотнесение групп пояснений с разными способами решений.

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м.

3 часть площади занята цветами, а остальная часть – овощами и ягодами.

Чему равна площадь участка, занятая овощами и ягодами?»

1) 120 * 85 = 10200 (кв.м ) длина участка, занятого цветами

2) 120 : 3 = 40 (м) площадь участка с цветами

3) 40 * 85 = 3400 (кв.м ) площадь участка, занятого овощами и ягодами

4) 10200 – 3400 = 6800 (кв.м ) длина участка с цветами

8) Установление соответствия между содержанием задачи и её краткой записью (в виде чертежа, рисунка, таблицы и т. д.) и, наоборот, между краткой записью и содержанием.

- Соответствует ли схематический рисунок (чертёж, таблица,…) данной задаче? Обоснуйте свой ответ.

- Как нужно изменить рисунок (чертёж, таблицу,…), чтобы он соответствовал данной задаче?

9) Выбор среди нескольких схематических моделей (чертежей, таблиц, ….) той, которая соответствует данной задаче.

10) Выбор равенства, являющегося решением задачи. Обоснование выбора.

«В двух гнёздах скворцов 11 птенцов. Из одного гнезда уже вылетело 6 скворцов, из другого 4. Скольким скворчатам ещё предстоит вылететь?»

1) 11 – 6 – 4 = 1 (ск.) 2) 11 + (6+4)= 21(ск.)

3) (11 – 6) + 4 =9 (ск.) 4) 11 – (6+ 4)= 1 (ск.)

11) Изменение текста задачи в соответствии с данным решением.

12) Нахождение ложного способа решения.

«Нужно покрасить 150 рам. Один маляр может это сделать за 15 дней. Другой – за 10 дней. За сколько дней выполнят эту работу оба маляра, если будут работать вместе?»

1 способ 2 способ

1. 15 + 10 = 25 (д.) 1. 150 : 15 = 10 (р.)

2. 150 : 25 = 6 (д.) 2. 150 : 10 = 15 (р.)

3. 10 + 15 = 25 (р.)

4. 150 : 25 = 6 (д.)

13) Продолжение решения задачи.

«Заяц за 3 прыжка преодолел расстояние в 13 м. Первый прыжок составил 3 м, второй 5 м. Сколько метров преодолел заяц в третьем прыжке?»

1. 3 + 5 = 8(м) -……..

2.

14) Объяснение выражений, составленных по данному условию.

Например:

-Определи смысл составленных по задаче математических выражений, запиши пояснения

к каждому выражению.

- Выбери выражение, являющееся решением задачи.

«В вагоне поезда было 35 пассажиров. На станции вышли 7 пассажиров, а вошли 6.»

35 – 7 7 + 6 35 – ( 7+ 6)

35 + 6 7 - 6 35 – 7 + 6

15) Составление выражений по вопросам к данному условию.

Запиши выражением ответ на каждый вопрос:

«На турбазе 8 маленьких палаток и 5 больших. Маленькие палатки вмещают 4 человека, а большие – 10. Сколько человек может разместиться во всех этих палатках?»

Сколько всего человек вмещают маленькие палатки?______________________

Сколько всего больших и маленьких палаток на турбазе?___________________

На сколько больших палаток …, чем маленьких?___________________________

Сколько человек вмещает маленькая палатка?____________________________

Сколько всего человек вместят большие палатки?________________________

На сколько больше человек вмещают большие палатки, чем маленькие?______

Сколько всего человек вместят одна большая и маленькая палатки?_________

Одной из главных причин, по которым школьники неверно решают ту или иную задачу, является неспособность глубоко, осмысленно, внимательно проанализировать то, что дано в задаче(данные) и то, что нужно узнать(вопрос), и взаимосвязи между ними. Учитель при этом постоянно напоминает детям: «Внимательно читайте условие и вопрос». Но ошибки продолжают существовать. Данный приём направлен на формирование у учащихся умения более глубоко, осмысленно подходить к анализу задачи, чётко выделять известные и неизвестные величины. При составлении вопросов используются вопросы с «подвохом» (неверно сформулированные). Для того, чтобы это заметить, учащимся нужно глубоко проанализировать взаимосвязи между данными задачи. Также используются вопросы, для ответа на которые не требуется составления выражения, так как нужно узнать то, что изначально известно

16) Составление и определение смысла всевозможных выражений (в том числе и не имеющих смысла в рамках данной задачи) из чисел, данных в условии задачи.

Этот приём трудоёмкий, но очень полезный. При его использовании учащиеся учатся глубокому анализу числовых данных задачи, взаимосвязей между ними.

- Составь как можно больше числовых выражений с данными задачи, объясни их смысл ;

- Из числовых данных задачи и значений ранее составленных выражений составь другие выражения и объясни их смысл;

- Выбери те выражения, значения которых помогают ответить на вопрос задачи;

- Выпиши в отдельные столбцы выражения, которые имеют смысл и, которые смысла не имеют.

Например:

«На турбазе 8 маленьких палаток и 5 больших. Маленькие палатки вмещают 4 человека, а большие – 10. Сколько человек может разместиться во всех этих палатках?»

8 – 5 – на столько больше маленьких палаток, чем больших

8 + 5 – больших и маленьких палаток

8 * 5 – не имеет смысла

8 : 5 – не имеет смысла

4 + 10 – всего человек вмещает 1 большая и 1 маленькая палатка

10 – 4 – на столько человек больше вмещает большая палатка, чем маленькая

10 * 4 – не имеет смысла

10 : 4 – не имеет смысла

8 : 4 – не имеет смысла

8 + 4 – не имеет смысла

8 – 4 – не имеет смысла

8 * 4 – всего человек в маленьких палатках

4 * 8 – не имеет смысла

10 – 5 – не имеет смысла

10 + 5 – не имеет смысл

10 : 5 – не имеет смысла

10 * 5 – всего человек в больших палатках

5 * 10 – не имеет смысла

8 – 5 + 8 – не имеет смысла

8 – 5 + 5 – не имеет смысла

(8 – 5) + (8+ 5) – не имеет смысла

(8 - 5)+ (10 – 4) – не имеет смысла

( 8 * 4)+ (10 * 5)- всего человек в палатках

17) Составление задач: - по иллюстрации;

- по краткой записи (рисунку, чертежу, таблице, опорным словам);

- по данной записи решения;

- по предложенной программе действий, по «Дереву рассуждений»;

- по некоторым исходным данным: с числовыми данными 20, 25, 3;

- с определёнными условиями: в 3 действия, в ответе - 120 кг; со словами «больше на…» и т. д.

Учитель начальных классов МБОУ СОШ мкр.Вынгапуровский Гергард Инга Леонидовна

Исследовательская работа над уже решенной задачей

Развитие информационного общества, научно-технические преобразования, рыночные отношения требуют от каждого человека высокого уровня профессиональных и деловых качеств, предприимчивости, способности ориентироваться в сложных ситуациях, быстро и безошибочно принимать решения.

В Федеральном Государственном Образовательном стандарте отмечена необходимость привести школьное образование в соответствие с потребностями времени, современного общества, которое характеризуется изменчивостью, многообразием существующих в нем связей, широким внедрением информационных технологий.

Совершенно очевидно, что школа не в состоянии обеспечить ученика знаниями на всю жизнь, он она может и должна вооружить его методами познания, сформировать познавательную самостоятельность.

В формировании многих качеств, необходимых успешному современному человеку, может большую роль сыграть школьная дисциплина - математика. На уроках математики школьники учатся рассуждать, доказывать, находить рациональные пути выполнения заданий, делать соответствующие выводы. Общепризнанно, что «математика - самый короткий путь к самостоятельному мышлению», «математика ум в порядок приводит» как отмечал М.В. Ломоносов.

Тревогу о будущем своих учеников всегда испытывают учителя, выпуская их в мир взрослых. Во многом на учителях лежит ответственность за желание детей учиться, за качество их образования, а в конечном итоге за успешную социализацию после окончания школы.

Школьнику необходимо получить достойное образование, уметь на протяжении всей своей жизни обновлять и пополнять знания, уметь реализовать свои лучшие качества, чтобы быть успешным.

Учителя ищут эффективные пути и средства развития потенциальных возможностей школьников. Сейчас в школьной практике активно используются технологии развивающего обучения, согласно которым учитель не преподносит истину, а учит ее находить.

Основным методом всех технологий развивающего обучения является исследовательская деятельность учащихся.

Говорят: «Новое - хорошо забытое старое». Одним из самых первых сторонников метода открытия или исследования как основы обучения считают Яна Амоса Коменского. Но, пожалуй, самыми пламенными защитниками этого метода были российские педагоги и психологи начала XX века Василиц Порфирьевич Вахтеров и Лев Семенович Выготский.

И сегодня очень актуально звучат слова В.П. Вахтерова о том, что образован не тот, кто много знает, а тот, кто хочет много знать, и умеет добывать эти знания.

Он подчеркивал исключительную важность мыслительных умений школьников - умения анализировать, сравнивать, комбинировать, обобщать и делать выводы; важность умения пользоваться приемами научного исследования, хотя бы и в самой элементарной форме.

Каждому ребенку дарована от природы склонность к познанию и исследованию окружающего мира. Правильно поставленное обучение должно совершенствовать эту склонность, способствовать развитию соответствующих умений и навыков. Подготовка ребенка к исследовательской деятельности, обучение его умениям и навыкам исследовательского поиска становится важнейшей задачей образования и современного учителя.

Закладка основных, содержательных линий математического образования, включающего в себя, в том числе и общие исследовательские умения, происходит также на начальном этапе обучения. Уже на начальном этапе изучения математики возможно использование элементов учебных математических исследований, организованных как задания исследовательского характера.

Цель: обосновать необходимость использования заданий исследовательского характера на уроках математики как средства развития исследовательской деятельности младших школьников и систематизировать методические рекомендации по использованию подобных заданий.

Сразу отметим, что многие методисты считают последующую и творческую работу над задачами аналогичными. На наш взгляд, это не верно. Во время последующей решению работы над задачей можно выполнять исследовательские творческие задания с уже решенной задачей, однако не всякая творческая работа над задачей является последующей решению.

При организации деятельности учащихся над задачей после ее решения (последующей) можно использовать следующие виды работы:

На мой взгляд, этот этап является очень важным и интересным, хотя зачастую он опускается. Именно работа над задачей на данном этапе способствует развитию творческой активности и мышления учащихся, повышает интерес к математике, к решению задач, позволяет целенаправленнее формировать компоненты общего умения решать задачи.

Приёмы работы над задачей на данном этапе:

Эти приёмы также способствуют развитию умения производить анализ задачи, устанавливать взаимосвязи между величинами, осознанно выбирать действие при решении задач.

1) Решение задачи другим способом (если это возможно), сравнение разных способов решения;

«Длина пришкольного участка прямоугольной формы 120 м, а ширина 85 м.

3 часть площади занята цветами, а остальная часть – овощами и ягодами.

Чему равна площадь участка, занятая овощами и ягодами?»

1 способ

1) 120 * 85 = 10200 (кв.м ) – S участка

2) 10200 : 3 = 3400 (кв.м ) – занято цветами

3) 10200 – 3400 = 6800 (кв.м )

2 способ

1) 120 * 85 = 10200 (кв.м) – S участка

2) 120 : 3 = 40 (м) – длина участка, занятого цветами

3) 40 * 85 = 3400 (кв.м) – Sучастка, занятого цветами

4) 10200 – 3400 = 6800 (кв.м )

3 способ

1) 120 : 3 = 40 (м) – длина участка, занятого цветами

2) 120 – 40 = 80 (м) – длина участка, занятого овощами и ягодами

3) 85 * 80 = 6800 (кв. м)

4 способ

1) 120 : 3 = 40 (м) – длина участка, занятого цветами

2) 40 * 85 = 3400 (кв. м) – S участка, занятого цветами

3) 3400 * 2 = 6800 (кв. м)

5 способ

1) 120 * 85 = 10200 (кв.м) – S участка

2) 10200 : 3 = 3400 (кв.м) – S участка, занятого цветами

3) 3400 * 2 = 6800 (кв. м)

6 способ

1) 120 : 3 = 40 (м) – длина участка, занятого цветами

2) 40 * 2 = длина участка, занятого овощами и ягодами

3) 80 * 85 = 6800 (кв. м)

2) Составление аналогичной задачи с новыми данными.

Этот приём помогает детям переносить известную схему решения на другие задачи этого вида, учит обобщать их в группы.

3) Постановка дополнительных вопросов к решённой задаче.

Этот приём предполагает постановку дополнительных вопросов, замену известных величин неизвестными, поиск новых решений.

«Два лыжника вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 66 км. Скорость первого -12 км/ч, второго – 10 км/ч. Через какое время они встретятся?»

Что ещё можно узнать по имеющимся в тексте задачи и полученным данным?

На сколько скорость первого лыжника больше скорости второго лыжника?

Сколько км прошёл до встречи первый лыжник?

Сколько км прошёл до встречи второй лыжник?

На сколько км больше прошёл до встречи первый лыжник?

На каком расстоянии друг от друга будут лыжники через 1 час после встречи, через 2 часа после встречи? и т. д.

4) Изменение вопроса задачи.

- Измени вопрос так, чтобы задача решалась в одно действие, в два действия.

- Измени вопрос так, чтобы задача решалась вычитанием (делением, …).

Этот приём позволяет решить несколько задач по одному и тому же условию (при решении составных задач), тем самым экономя время, которое тратится на осмысление условия.

Например:

«В первый день улитка проползла 5 м, во второй на 2 м больше. Сколько метров проползла улитка во второй день?»

Измени вопрос задачи так, чтобы задача решалась в два действия.

5) Изменение условия задачи так, чтобы задача решалась другим действием.

6) Изменение числовых данных задачи так, чтобы появился новый способ решения.

7) Исследование решения.

Сколько способов решения имеет задача? При каких условиях она не имела бы решения? Какие приёмы целесообразны для поиска решения задачи?

8) Сравнение задач и их решения. Этот приём позволяет глубже осознать взаимосвязи между величинами, входящими в задачу, способствует лучшему усвоению идеи решения, формированию осознанного подхода к анализу задачи, выбору действий. Дети определяют, что одно и то же слово, один и тот же вопрос не определяют выбор действия и, что для этого нужно установить связи между величинами и на их основе выбрать, а затем выполнить действие.

Сравнение задач вырабатывает у учащихся привычку не начинать поиск решения задачи без глубокого, полного анализа задачи.

Проводя такого рода работу, ученики анализируют и систематизируют, сравнивают и обобщают, систематизируют и классифицируют, т.е. используют логику. Таким образом, в работе с уже решенной задачей заложены большие возможности для развития мышления учащихся.

Кроме основного вида работы над задачей – её решения, можно использовать и другие виды работы, не включающие явное и полное решение задач, но способствующие формированию комплекса умений, необходимых для плодотворного решения задач, развитию мышления, творческой активности, познавательного интереса.

Нестандартные задачи и их виды

Учитель начальных классов

МБОУ СОШ №3

Екатерина Тимошенко

Понятие «нестандартная задача» используется многими методистами. Так, Ю. М. Колягин раскрывает это понятие следующим образом: «Под нестандартной понимается задача, при предъявлении которой учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение».

Определение нестандартной задачи приведено также в книге «Как научиться решать задачи» авторов Л.М. Фридмана, Е.Н. Турецкого: «Нестандартные задачи - это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения».

Не следует путать нестандартные задачи с задачами повышенной сложности. Условия задач повышенной сложности таковы, что позволяют ученикам довольно легко выделить тот математический аппарат, который нужен для решения задачи по математике. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач этого типа. А вот нестандартная задача предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого - решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 5 классе нестандартна, а в 6 классе она является обычной, и даже не повышенной сложности.

Анализ учебников и учебных пособий по математике показывает, что каждая текстовая задача в определенных условиях может быть нестандартной, а в других - обычной, стандартной. Стандартная задача одного курса математики может быть нестандартной в другом курсе.

Опираясь на анализ теории и практики использования нестандартных задач в обучении математике, можно установить их общую и специфическую роль. Нестандартные задачи:

• учат детей использовать не только готовые алгоритмы, но и самостоятельно находить новые способы решения задач, т.е. способствуют умению находить оригинальные способы решения задач;

• оказывают влияние на развитие смекалки, сообразительности учащихся;

• препятствуют выработке вредных штампов при решении задач, разрушают неправильные ассоциации в знаниях и умениях учащихся, предполагают не столько усвоение алгоритмических приемов, сколько нахождение новых связей в знаниях, к переносу знаний в новые условия, к овладению разнообразными приемами умственной деятельности;

• создают благоприятные условия для повышения прочности и глубины знаний учащихся, обеспечивают сознательное усвоение математических понятий.

Нестандартные задачи:

• не должны иметь уже готовых, заученных детьми алгоритмов;

• должны быть доступны по содержанию всем учащимся;

• должны быть интересными по содержанию;

• для решения нестандартных задач учащимся должно хватать знаний, усвоенных ими по программе.

Решение нестандартных задач активизирует деятельность учащихся. Учащиеся учатся сравнивать, классифицировать, обобщать, анализировать, а это способствует более прочному и сознательному усвоению знаний.

Как показала практика, нестандартные задачи весьма полезны не только для уроков, но и для внеклассных занятий, для олимпиадных заданий, так как при этом открывается возможность по-настоящему дифференцировать результаты каждого участника. Такие задачи могут с успехом использоваться и в качестве индивидуальных заданий для тех учеников, которые легко и быстро справляются с основной частью самостоятельной работы на уроке, или для желающих в качестве дополнительных заданий. В результате учащиеся получают интеллектуальное развитие и подготовку к активной практической деятельности.

Общепринятой классификации нестандартных задач нет, но Б.А. Кордемский выделяет следующие виды таких задач:

• Задачи, примыкающие к школьному курсу математики, но повышенной трудности - типа задач математических олимпиад. Предназначаются в основном для школьников с определившимся интересом к математике; тематически эти задачи обычно связаны с тем или иным определённым разделом школьной программы. Относящиеся сюда упражнения углубляют учебный материал, дополняют и обобщают отдельные положения школьного курса, расширяют математический кругозор, развивают навыки в решении трудных задач.

• Задачи типа математических развлечений. Прямого отношения к школьной программе не имеют и, как правило, не предполагают большой математической подготовки. Это не значит, однако, что во вторую категорию задач входят только лёгкие упражнения. Здесь есть задачи с очень трудным решением и такие задачи, решение которых до сих пор не получено. «Нестандартные задачи, поданные в увлекательной форме, вносят эмоциональный момент в умственные занятия. Не связанные с необходимостью всякий раз применять для их решения заученные правила и приёмы, они требуют мобилизации всех накопленных знаний, приучают к поискам своеобразных, не шаблонных способов решения, обогащают искусство решения красивыми примерами, заставляют восхищаться силой разума».

К этому виду задач относятся:

• разнообразные числовые ребусы («… примеры, в которых все или некоторые цифры заменены звездочками или буквами. Одинаковые буквы заменяют одинаковые цифры, разные буквы - разные цифры» и головоломки на смекалку;

• логические задачи, решение которых не требует вычислений, но основывается на построении цепочки точных рассуждений;

• задачи, решение которых основывается на соединении математического развития и практической смекалки: взвешивание и переливания при затруднительных условиях;

• математические софизмы - это умышленное, ложное умозаключение, которое имеет видимость правильного. (Софизм - доказательство ложного утверждения, причём ошибка в доказательстве искусно замаскирована. Софизм в переводе с греческого означает хитроумную выдумку, ухищрение, головоломку);

• задачи-шутки;

• комбинаторные задачи, в которых рассматриваются различные комбинации из заданных объектов, удовлетворяющие определённым условиям (Б.А. Кордемский, 1958).

Не менее интересна классификация нестандартных задач, приведённая И.В. Егорченко:

• задачи, направленные на поиск взаимосвязей между заданными объектами, процессами или явлениями;

• задачи, неразрешимые или не решаемые средствами школьного курса на данном уровне знаний учащихся;

• задачи, в которых необходимо:

проведение и использование аналогий, определение различий заданных объектов, процессов или явлений, установление противоположности заданных явлений и процессов или их антиподов;

• осуществление практической демонстрации, абстрагирование от тех или иных свойств объекта, процесса, явления или конкретизации той или иной стороны данного явления;

• установка причинно-следственных отношений между заданными объектами, процессами или явлениями;

• построение аналитическим или синтетическим путем причинно-следственных цепочек с последующим анализом получившихся вариантов;

• правильное осуществление последовательности определенных действий, избегая ошибок-«ловушек»;

• осуществление перехода от плоскостного к пространственному варианту заданного процесса, объекта, явления или наоборот (И.В. Егорченко, 2003).

Итак, единой классификации нестандартных задач нет. Их существует несколько, но автор работы использовал в исследовании классификацию, предложенную И.В. Егорченко.

Методы решения нестандартных задач

Русский филолог Дмитрий Николаевич Ушаков в своём толковом словаре даёт такое определение понятия «метод» - путь, способ, прием теоретического исследования или практического осуществления чего-нибудь (Д. Н. Ушаков, 2000).

Каковы же методы обучения решению задач по математике, которые мы считаем на данный момент нестандартными? Универсального рецепта, к сожалению, никто не придумал, учитывая уникальность данных задач. Некоторые учителя натаскивают в шаблонных упражнениях. Происходит это следующим образом: учитель показывает способ решения, а затем ученик повторяет это при решении задач многократно. При этом убивается интерес учащихся к математике, что, по меньшей мере, печально.

В математике нет каких-либо общих правил, позволяющих решить любую нестандартную задачу, так как такие задачи в какой-то степени неповторимы. Нестандартная задача в большинстве случаев воспринимается как «вызов интеллекту, и порождает потребность реализовать себя в преодолении препятствия, в развитии творческих способностей» [8, с. 32].

Рассмотрим, несколько методов решения нестандартных задач:

• алгебраический;

• арифметический;

• метод перебора;

• метод рассуждения;

• практический;

• метод предположения.

Алгебраический метод решения задач развивает творческие способности, способность к обобщению, формирует абстрактное мышление и обладает такими преимуществами, как краткость записи и рассуждений при составлении уравнений, экономит время.

Для того чтобы решить задачу алгебраическим методом необходимо:

• провести разбор задачи с целью выбора основного неизвестного и выявления зависимости между величинами, а также выражения этих зависимостей на математическом языке в форме двух алгебраических выражений;

• найти основание для соединения этих выражений знаком «=» и составить уравнение;

• найти решения полученного уравнения, организовать проверку решения уравнения.

Все эти этапы решения задачи логически связаны между собой. Например, о поисках основания для соединения двух алгебраических выражений знаком равенства мы упоминаем как об особом этапе, но ясно, что на предыдущем этапе указанные выражения образуются не произвольно, а с учётом возможности соединить их знаком «=».

Как выявление зависимостей между величинами, так и перевод этих зависимостей на математический язык требует напряжённой аналитико-синтетической мыслительной деятельности. Успех в этой деятельности зависит, в частности от того, знают ли учащиеся, в каких отношениях вообще могут находиться эти величины, и понимают ли они реальный смысл этих отношений (например, отношений, выраженных терминами «позже на…», «старше в…раз» и т.п.). Далее требуется понимание, каким именно математическим действием или, свойством действия или какой связью (зависимостью) между компонентами и результатом действия может быть описано то или иное конкретное отношение.

Приведём пример решения нестандартной задачи алгебраическим методом.

Задача. Рыбак поймал рыбу. Когда у него спросили: «Какова её масса?», он ответил: «Масса хвоста - 1кг, масса головы такая же, как масса хвоста и половины туловища. А масса туловища такая, как масса головы и хвоста вместе». Какова масса рыбы?

Решение: Пусть х кг - масса туловища; тогда (1+1/2х) кг - масса головы. Так как по условию масса туловища равна сумме масс головы и хвоста, составляем и решаем уравнение: х = 1 + 1/2х + 1,

х - 1/2х =2,

х/2 = 2,

х = 4.

4 кг - масса туловища, тогда 1+1/2 • 4=3 (кг) - масса головы и 3+4+1=8 (кг) - масса всей рыбы; Ответ: 8 кг.

Арифметический метод решения также требует большого умственного напряжения, что положительно сказывается на развитии умственных способностей, математической интуиции, на формировании умения предвидеть реальную жизненную ситуацию.

Рассмотрим пример решения нестандартной задачи арифметическим методом:

Задача. У двух рыбаков спросили: «Сколько рыбы в ваших корзинах?»

«В моей корзине половина того, что в корзине у него, да ещё 10», - ответил первый. «А у меня в корзине столько, сколько у него, да ещё 20», - подсчитал второй. Мы сосчитали, а теперь посчитайте вы.

Решение.

Построим схему к задаче. Обозначим первым отрезком схемы количество рыбы у первого рыбака. Вторым отрезком обозначим количество рыбы у второго рыбака.

В связи с тем, что современному человеку необходимо иметь представление об основных методах анализа данных и вероятностных закономерностях, играющих важную роль в науке, технике и экономике, в школьный курс математики вводят элементы комбинаторики, теории вероятностей и математической статистики, в которых удобно разбираться при помощи метода перебора.

Включение комбинаторных задач в курс математики оказывает положительное влияние на развитие школьников. «Целенаправленное обучение решению комбинаторных задач способствует развитию такого качества математического мышления, как вариативность. Под вариативностью мышления мы понимаем направленность мыслительной деятельности ученика на поиск различных решений задачи в случае, когда нет специальных указаний на это».

Комбинаторные задачи можно решать различными методами. Условно эти методы можно разделить на «формальные» и «неформальные». При «формальном» методе решения нужно определить характер выбора, выбрать соответствующую формулу или комбинаторное правило (существуют правила суммы и произведения), подставить числа и вычислить результат. Результат - это количество возможных вариантов, сами же варианты в этом случае не образовываются.

При «неформальном» же методе решения на первый план выходит сам процесс составления различных вариантов. И главное уже не сколько, а какие варианты могут получиться. К таким методам относится метод перебора. Этот метод доступен даже младшим школьникам, и позволяет накапливать опыт практического решения комбинаторных задач, что служит основой для введения в дальнейшем комбинаторных принципов и формул. Кроме того, в жизни человеку приходится не только определять число возможных вариантов, но и непосредственно составлять все эти варианты, а, владея приёмами систематического перебора, это можно сделать более рационально.

Задачи по сложности осуществления перебора делятся на три группы:

1. Задачи, в которых нужно произвести полный перебор всех возможных вариантов.

2. Задачи, в которых использовать приём полного перебора нецелесообразно и нужно сразу исключить некоторые варианты, не рассматривая их (то есть осуществить сокращённый перебор).

3. Задачи, в которых операция перебора производится несколько раз и по отношению к разного рода объектам.

Приведём соответствующие примеры задач:

Задача. Расставляя знаки «+» и «-» между данными числами 9…2…4, составь все возможные выражения.

Решение.

Проводится полный перебор вариантов:

а) два знака в выражении могут быть одинаковыми, тогда получаем:

9 + 2 + 4 или 9 - 2 - 4;

б) два знака могут быть разными, тогда получаем:

9 + 2 - 4 или 9 - 2 + 4.

Задача. Учитель говорит, что он нарисовал в ряд 4 фигуры: большой и маленький квадраты, большой и маленький круги так, что на первом месте находится круг и одинаковые по форме фигуры не стоят рядом, и предлагает ученикам отгадать, в какой последовательности расставлены эти фигуры.

Решение.

Всего существует 24 различных расположения этих фигур. И составлять их все, а потом выбирать соответствующие данному условию нецелесообразно, поэтому проводится сокращённый перебор.

На первом месте может стоять большой круг, тогда маленький может быть только на третьем месте, при этом большой и маленький квадраты можно поставить двумя способами - на второе и четвёртое место.

Аналогичное рассуждение проводится, если на первом месте стоит маленький круг, и также составляются два варианта.

Задача. Три компаньона одной фирмы хранят ценные бумаги в сейфе, на котором 3 замка. Компаньоны хотят распределить между собой ключи от замков так, чтобы сейф мог открываться только в присутствии хотя бы двух компаньонов, но не одного. Как это можно сделать?

Решение.

Сначала перебираются все возможные случаи распределения ключей. Каждому компаньону можно дать по одному ключу или по два разных ключа, или по три.

Предположим, что у каждого компаньона по три разных ключа. Тогда сейф сможет открыть один компаньон, а это не соответствует условию.

Предположим, что у каждого компаньона по одному ключу. Тогда, если придут двое из них, то они не смогут открыть сейф.

Дадим каждому компаньону по два разных ключа. Первому - 1 и 2 ключи, второму - 1 и 3 ключи, третьему - 2 и 3 ключи. Проверим, когда придут любые два компаньона, смогут ли они открыть сейф.

Могут прийти первый и второй компаньоны, у них будут все ключи (1 и 2, 1 и 3). Могут прийти первый и третий компаньоны, у них также будут все ключи (1 и 2, 2 и 3). Наконец, могут прийти второй и третий компаньоны, у них тоже будут все ключи (1 и 3, 2 и 3).

Таким образом, чтобы найти ответ в этой задаче, нужно выполнить операцию перебора несколько раз.

При отборе комбинаторных задач нужно обращать внимание на тематику и форму представления этих задач. Желательно, чтобы задачи не выглядели искусственным, а были понятны и интересны детям, вызывали у них положительные эмоции. Можно для составления задач использовать практический материал из жизни.

Встречаются и другие задачи, которые можно решить методом перебора.

В качестве примера решим задачу: «Маркизу Карабасу было 31 год, а его молодому энергичному Коту в Сапогах 3 года, когда произошли известные по сказке события. Сколько лет произошло с тех пор, если сейчас Кот в три раза младше своего хозяина?» Перебор вариантов представим таблицей.

Возраст Маркиза Карабаса и Кота в Сапогах

М. 31 32 33 34 35 36 37 38 39 40 41 42

К. 3 4 5 6 7 8 9 10 11 12 13 14

Во ? раз - - - - - - - - - - - +

14 - 3 = 11 (лет)

Ответ: 11 лет прошло.

При этом ученик как бы экспериментирует, наблюдает, сопоставляет факты и на основании частных выводов делает те или иные общие заключения. В процессе этих наблюдений обогащается его реально-практический опыт. Именно в этом и состоит практическая ценность задач на перебор. При этом слово «перебор» используется в смысле разбора всех возможных случаев, которые удовлетворяют условиям задачи, показав, что других решений быть не может.

Эту задачу можно решить и алгебраическим методом.

Пусть Коту х лет, тогда Маркизу 3х, исходя из условия задачи, составим уравнение:

3х - х = 28,

2х = 28,

х = 28: 2,

х = 14.

Коту сейчас 14 лет, тогда прошло 14 - 3 = 11(лет).

Ответ: 11 лет прошло.

Метод рассуждений можно использовать для решения математических софизмов.

Ошибки, допущенные в софизме, обычно сводятся к следующим: выполнению «запрещённых» действий, использованию ошибочных чертежей, неверному словоупотреблению, неточности формулировок, «незаконным» обобщениям, неправильным применениям теорем.

Раскрыть софизм - это, значит, указать ошибку в рассуждении, основываясь на которой была создана внешняя видимость доказательства.

Разбор софизмов, прежде всего, развивает логическое мышление, прививает навыки правильного мышления. Обнаружить ошибку в софизме - это, значит, осознать её, а осознание ошибки предупреждает от повторения её в других математических рассуждениях. Помимо критичности математического мышления этот вид нестандартных задач выявляет гибкость мышления. Сумеет ли ученик «вырваться из тисков» этого строго логичного на первый взгляд пути, разорвать цепь умозаключений в том самом звене, которое является ошибочным и делает ошибочным все дальнейшие рассуждения?

Разбор софизмов помогает также сознательному усвоению изучаемого материала, развивает наблюдательность и критическое отношение к тому, что изучается.

а) Вот, к примеру, софизм с неправильным применением теоремы.

Докажем, что 2 • 2 = 5.

Возьмём в качестве исходного соотношения следующее очевидное равенство: 4 : 4 = 5 : 5 (1)

Вынесем за скобки общий множитель в левой и правой частях, получим:

4 • (1 : 1) = 5 • (1 : 1) (2)

Числа в скобках равны, значит, 4 = 5 или 2 • 2 = 5.

Решение.

В рассуждении при переходе от равенства (1) к равенству (2) создана иллюзия правдоподобия на основе ложной аналогии с распределительным свойством умножения относительно сложения.

б) Софизм с использованием «незаконных» обобщений.

Имеются две семьи - Ивановых и Петровых. Каждая состоит из 3 человек - отца, матери и сына. Отец Иванов не знает отца Петрова. Мать Иванова не знает матери Петровой. Единственный сын Ивановых не знает единственного сына Петровых. Вывод: ни один член семьи Ивановых не знает ни одного члена семьи Петровых. Верно ли это?

Решение.

Если член семьи Ивановых не знает равного себе по семейному статусу члена семьи Петровых, то это не значит, что он не знает всю семью. Например, отец Иванов может знать мать и сына Петровых.

Метод рассуждений можно использовать и для решения логических задач. Под логическими задачами обычно понимают такие задачи, которые решаются с помощью одних лишь логических операций. Иногда решение их требует длительных рассуждений, необходимое направление которых заранее нельзя предугадать.

Задача. Говорят, что Тортила отдала золотой ключик Буратино не так просто, как рассказал А. Н. Толстой, а совсем иначе. Она вынесла три коробочки: красную, синюю и зелёную. На красной коробочке было написано: «Здесь лежит золотой ключик», а на синей - «Зелёная коробочка пуста», а на зелёной - «Здесь сидит змея». Тортила прочла надписи и сказала: «Действительно в одной коробочке лежит золотой ключик, в другой - змея, а третья - пуста, но все надписи неверны. Если отгадаешь, в какой коробочке лежит золотой ключик, он твой». Где лежит золотой ключик?

Решение.

Так как все надписи на коробочках неверны, то в красной коробочке лежит не золотой ключик, зеленая коробочка не пустая и в ней не змея, значит в зеленой коробочке - ключик, в красной - змея, а синяя - пуста.

При решении логических задач активизируется логическое мышление, а это умение выводить следствия из посылок, которое крайне необходимо для успешного овладения математикой.

Ребус - это загадка, но загадка не совсем обычная. Слова и числа в математических ребусах изображены при помощи рисунков, звездочек, цифр и различных знаков. Чтобы прочесть то, что зашифровано в ребусе, надо правильно назвать все изображенные предметы и понять, какой знак что изображает. Ребусами люди пользовались еще тогда, когда не умели писать. Свои письма они составляли из предметов. Например, вожди одного племени послали однажды своим соседям вместо письма птицу, мышь, лягушку и пять стрел. Это означало: «Умеете ли летать как птицы и прятаться в земле как мыши, прыгать по болотам как лягушки? Если не умеете, то не пробуйте воевать с нами. Мы засыпим вас стрелами, как только вы вступите в нашу страну».

Решение.

Судя по первой букве суммы 1), Д = 1 или 2.

Предположим, что Д = 1. Тогда, У ? 5. У = 5 исключаем, т.к. Р не может быть равно 0. У ? 6, т.к. 6 + 6 = 12, т.е. Р = 2. Но такое значение Р при дальнейшей проверке не подходит. Аналогично, У ? 7.

Предположим, что У = 8. Тогда, Р = 6, А = 2, К = 5, Д = 1.

Магический (волшебный) квадрат - это квадрат, в котором сумма чисел по вертикали, горизонтали и диагонали получается одинаковой.

Задача. Расположите числа от 1 до 9 так, чтобы по вертикали, горизонтали и диагонали получилась одинаковая сумма чисел, равная 15.

Решение.

Хотя общих правил для решения нестандартных задач нет (поэтому эти задачи и называются нестандартными), однако мы постарались дать ряд общих указаний - рекомендаций, которыми следует руководствоваться при решении нестандартных задач разных видов.

Каждая нестандартная задача оригинальна и неповторима в своём решении. В связи с этим разработанная методика обучения поисковой деятельности при решении нестандартных задач не формирует навыки решения нестандартных задач, речь может идти лишь об отработке определённых умений:

• умения понимать задачу, выделять главные (опорные) слова;

• умения выявлять условие и вопрос, известное и неизвестное в задаче;

• умения находить связь между данным и искомым, то есть проводить анализ текста задачи, результатом которого является выбор арифметического действия или логической операции для решения нестандартной задачи;

• умения записывать ход решения и ответ задачи;

• умения проводить дополнительную работу над задачей;

• умение отбирать полезную информацию, содержащуюся в самой задаче, в процессе её решения, систематизировать эту информацию, соотнося с уже имеющимися знаниями.

Нестандартные задачи развивают пространственное мышление, которое выражается в способности воссоздавать в уме пространственные образы объектов и выполнять над ними операции. Пространственное мышление проявляется при решении задач типа: «Сверху на кромке круглого торта поставили 5 точек из крема на одинаковом расстоянии друг от друга. Через все пары точек сделали разрезы. Сколько всего получилось кусочков торта?»

Практический метод можно рассмотреть для нестандартных задач на деление.

Задача. Палку нужно распилить на 6 частей. Сколько потребуется распилов?

Решение: Распилов потребуется 5.

При изучении нестандартных задач на деление надо понять: чтобы разрезать отрезок на Р частей, следует сделать (Р - 1) разрез. Этот факт нужно установить с детьми индуктивным путём, а затем использовать при решении задач.

Задача. В трёхметровом бруске - 300 см. Его надо разрезать на бруски длиной 50 см каждый. Сколько надо сделать разрезов?

Решение: Получаем 6 брусков 300 : 50 = 6 (брусков)

Рассуждаем так: чтобы разделить брусок пополам, т. е. на две части, надо сделать 1 разрез, на 3 части - 2 разреза и так далее, на 6 частей - 5 разрезов.

Итак, надо сделать 6 - 1 = 5 (разрезов).

Ответ: 5 разрезов.

Итак, одним из основных мотивов, побуждающих школьников учиться, является интерес к предмету. Интерес - это активная познавательная направленность человека на тот или иной предмет, явление и деятельность, созданная с положительным эмоциональным отношением к ним. Одним из средств развития интереса к математике являются нестандартные задачи. Под нестандартной задачей понимают такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Решение таких задач позволяет учащимся активно включиться в учебную деятельность. Существуют различные классификации задач и методов их решения. Самыми часто используемыми являются алгебраический, арифметический, практический методы и метод перебора, рассуждения и предположения.

Учитель начальных классов МБОУ СОШ мкр.Вынгапуровский Василенко Светлана Федоровна

Нестандартная задача как компонент начального математического образования

Какая задача по математике может называться нестандартной? Хорошее определение приведено в книге «Как научиться решать задачи» авторов Л.М. Фридмана, Е.Н. Турецкого.    

«Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения». Не следует путать их с задачами повышенной сложности. Условия задач повышенной сложности таковы, что позволяют ученикам довольно легко выделить тот математический аппарат, который нужен для решения задачи по математике. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач этого типа. А вот нестандартная задача предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого – решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 4 классе нестандартна, а в 5, 6 классах она является обычной, и даже не повышенной сложности.

Итак, если решение задачи учащийся не знает, на какой теоретический материал ему опираться, он тоже не знает, то в этом случае задачу по математике можно назвать нестандартной на данный период времени.

Традиционно нестандартными для младших школьников являются:

• некоторые виды арифметических текстовых задач (задачи на предположение, на движение мимо объектов с учетом их протяженности, на движение в одном направлении; задачи, решаемые способом уравнивания или замены данных, методом инверсии (т. е. с «конца»); задачи с неопределенными неизвестными);

• некоторые виды геометрических задач (деление фигур на части, составление фигуры из частей, преобразование фигур);

• логические задачи (на установление временных, пространственных, функциональных отношений; на активный перебор вариантов; на планирование деятельности; на установление сходства и отношения между элементами множеств; на оперирование категориями все, некоторые, отдельные); процессуальные задачи (задачи о переправах; задачи о переливаниях; задачи о взвешиваниях)

• комбинаторные задачи (на упорядочение предметов; на выбор подмножеств и их упорядочение; на определение количества различных вариантов; на выбор наилучшего результата по определенным критериям).

К тому же воспитание интереса младших школьников к математике, развитие их математических способностей невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических фокусов, числовых головоломок, арифметических ребусов и лабиринтов.

Характер указанных задач, уровень их трудности и сложности определяются реальными возможностями и потребностями учебного процесса, возрастными особенностями обучаемых и их математической подготовкой.

Нестандартная задача, как особый вид математических упражнений, является темой многих зарубежных и отечественных исследований. История вопроса уходит в глубину веков и восходит к «коллекциям проблем» египтян, греков, индийцев, китайцев, арабов.

В настоящее время исследованию процесса решения нестандартных задач посвящены работы психологов, педагогов, математиков (Д. Пойа, Л. М. Фридмана, Ю. М. Колягина и других), которые позволяют сделать вывод о том, что в процессе обучения решению задач развивается интеллект учащихся.

Решение задач имеет большое образовательное и воспитательное значение. Н. А. Мечинская и М. И. Моро отмечают, что решение задач всегда рассматривалось как такая учебная деятельность, которая преследует двоякую цель: во-первых, решение задач является средством, способствующим усвоению математических понятий и законов, а во-вторых, оно имеет самостоятельную ценность, поскольку служит для развития творческого мышления учащихся.

Внимание специалистов к нестандартным задачам определяется тем, что:

1. В их сюжетах находят отражение практические ситуации, знакомые ребенку, поэтому в рассуждениях он может опираться на свой жизненный опыт.

2. Задачи данной категории позволяют школьнику убедиться в прикладном характере математических методов, которыми он овладевает на уроках математики.

3. При их решении формируются общеучебные умения, необходимые для решения любой математической задачи, и навыки ориентировки в сложной ситуации, что позволяет считать нестандартные задачи мощным инструментом развития человеческого интеллекта.

4. Для решения нестандартных задач учащимся необходимо приложить определенные усилия, проявить волю, настойчивость, целеустремленность. Необычность приемов решения прививает вкус к самостоятельным исследованиям, к проявлению изобретательности, пробуждает положительные эмоции, как в процессе решения задач, так и при достижении результата.

Значимость нестандартных задач определяется тем, что они обеспечивают:

1) усвоение программных знаний на более высоком уровне, так как процесс их решения не связан с необходимостью применения заученных правил и приемов, а требует мобилизации всех накопленных знаний, приучает к поиску своеобразных, нешаблонных способов действия;

2) возможность выявления математических и общеинтеллектуальных способностей учащихся, установления уровня обученности и обучаемости, развития математического мышления, формирования познавательных интересов;

3) проверку способности и умения самостоятельно учиться.

Использованию в практике преподавания в начальной школе нестандартных математических задач предшествует большая подготовительная работа по их отбору. Поэтому необходимо сформулировать требования, на основе которых осуществляется отбор задач для начального математического образования. Критерии оценки качества задач школьного курса математики сформулированы Ю. М. Колягиным. Конкретизируем их с учетом специфики учебного опыта и возрастных особенностей учащихся начальных классов.

1. Задача, предъявляемая младшему школьнику, должна быть интересной и значимой для ученика, должна вызвать его желание к исследованию за счет:

- элементов новизны или занимательности в фабуле задачи как благоприятного фактора возбуждения интереса учеников к математике и мотивирования их интеллектуального труда;

- реальности описываемой в задаче ситуации, ее близости жизненному опыту ребенка;

- неожиданного, оригинального решения, требующего применения известных методов в необычных условиях, рационализации и упрощения уже известного приема.

2. Задача должна соответствовать возможностям учащихся начальных классов. Младший школьник должен не только хотеть, но и быть в состоянии решить предложенную задачу. Разочарование учеников слишком трудными математическими вопросами является одной из причин торможения их развития. Нерешенная задача отрицательно влияет на воспитание интереса к математике. Поэтому очень важно, особенно на начальном этапе обучения предмету, чтобы поставленные перед школьниками нестандартные задачи были ими успешно решены. Нестандартные задачи должны:

а) соответствовать по объему элементов и сложности их отношений уровню теоретических знаний и практическому опыту учащихся (в целях обеспечения возможности самостоятельного их решения или хотя бы его понимания);

б) иметь преимущественно лаконичные формулировки;

в) допускать практическое решение (необходимым условием этого является наличие небольших числовых данных), а также разные варианты решения и способы проверки его правильности. В то же время решение задачи не должно быть слишком легким, основанным на догадках, не требующих ни знаний, ни навыков практических действий.

3. Система нестандартных задач для начальной школы должна включать в себя все основные темы курса, тем самым обеспечивая отработку необходимых, предусмотренных программой знаний и умений, т. е. быть полной. Кроме этого, структурные характеристики задачи должны быть разноплановы: с полным (или недостаточным) набором условий, с наличием избыточных данных. Это приучает учеников не доверять внешнему облику задачи и не приступать к ее решению сразу, полагая, что внешний вид совпадает с действительным содержанием.

Эффективность обучения младших школьников решению нестандартных задач зависит, на наш взгляд, от нескольких условий. Во-первых, задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся. Во-вторых, необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения. В-третьих, нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.

Наша задача - уже в начальной школе показать каждому ребёнку, что математика - предмет яркий и увлекательный, а не скучный и занудный. К сожалению, изучение математики в младших классах зачастую сводится к решению примеров из учебников и вариантов всероссийских проверочных работ.

Нестандартные арифметические задачи и способы их решения.

1. При поиске решения незнакомой задачи полезно сделать чертеж или рисунок, т.к. именно он может быть способом решения задачи.

Задача 1. Бревно длиной 12 м распилили на 6 равных частей. Сколько распилов сделали?

Вывод: работа с чертежом является способом решения задачи.

1. Часть данных находят с помощью графических изображений (рисунков, чертежей), а часть - с помощью арифметических действий.

Задача 2. Ширина занавески для окна равна 1 м 20 см. Надо пришить 6 колец на одинаковом расстоянии друг от друга (первое и последнее кольца должны располагаться по краям занавески). Сколько сантиметров надо оставлять между кольцами?

120 : 5 = 24 (см)

1. Дополнительные построения или перестроения чертежей с учетом найденных чисел.

Задача 3. Муравей находится на дне колодца глубиной 30 м. За день он поднимается на 18 м, а за ночь сползает вниз на 12 м. Сколько дней нужно муравью, чтобы выбраться из колодца?

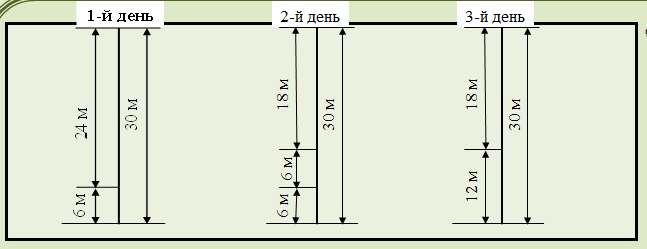
1. Введение вспомогательного элемента (часть)

Задача 4. Разложи 45 шариков в 4 коробки так, что если число шариков в третьей коробке увеличить в 2 раза, а в четвертой уменьшить в 2 раза, а в первой и второй оставить без изменения, то в каждой коробке будет одинаковое число шариков.

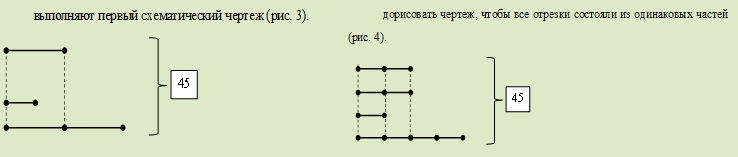
1. Использование способа подбора

Задача 5. Сумма четырех различных чисел равна 13. Наименьшее из этих чисел на 5 меньше наибольшего. Найди эти числа.

Встает проблема: можно ли решить эту задачу? Может быть, в ней не хватает данных?

Пробуем число 0. Тогда получаем: 0+ ? + ? + 5 = 13. Подберем пропущенные числа.

Их сумма равна 13 - 5 - 0 = 8. Эти числа должны быть разными и быть больше 0, но меньше 5. Между 0 и 5 идут числа 1, 2, 3, 4. Среди них нельзя выбрать два разных числа, дающих в сумме 8. Значит, число 0 не подходит.

Пробуем число 1. Тогда получаем: l + ?+ ?+ 6 = 13. Подбираем пропущенные числа.

Их сумма равна: 13 – 1 - 6 = 6. Между числами 1 и 6 стоят числа 2, 3, 4, 5. Среди них выбираем два, дающих в сумме 6. Это числа 2 и 4. Проверяем, правильно ли мы нашли четыре числа. Для этого складываем их: 1 + 2 + 4 + 6 = 13. Получили сумму, данную в задаче. Другие условия также соблюдены: числа различные, наименьшее из этих чисел 1, оно на 5 меньше наибольшего числа 6.

Получив один ответ, нужно проверить, нет ли других вариантов ответа.

Для этого пробуем число 2. Тогда получаем: 2 + ? + ? + 7 = 13. Подбираем пропущенные числа. Их сумма равна 4. Среди чисел 3, 4, 5, 6 нельзя выбрать два числа, дающих в сумме 4 (сумма любых двух перечисленных чисел больше 4). Можно проверить число 3 таким же образом. Числа, начиная с 4, проверять не нужно, так как сумма двух чисел получается равной или больше: 13 : 4 + ? + ? + 9 = 13.

Получаем ответ задачи: числа 1, 2, 4, 6.

1. Переформулировать задачу другими словами, чтобы она стала более понятной и знакомой.

Задача 6. Число яблок в корзине двузначное. Эти яблоки можно раздать поровну 2, 3 или 5 детям, но нельзя раздать поровну 4 детям. Сколько яблок в корзине? (Укажите такое наименьшее двузначное число.) Сначала ученики пытаются сделать рисунок или чертеж к задаче, но испытывают затруднения, так как на чертеже трудно показать, что нельзя раздать яблоки поровну 4 детям, следовательно, непонятно, как использовать чертеж для решения задачи. Тогда ученики начинают применять способ подбора. Учитель предлагает сначала изменить формулировку задачи, чтобы легче было выполнить подбор. Выясняется, что если яблоки можно раздать поровну 2, 3 и 5 детям, значит, число яблок делится на 2, 3. 5. Если яблоки нельзя раздать 4 детям поровну, значит, число яблок не делится на 4.

Задачу переформулируют следующим образом:

«Найди наименьшее двузначное число, которое делится на 2, 3,5 и не делится на 4»

Проверяют наименьшее двузначное число 10. Оно делится на 2 и 5, но не делится на 3, значит, число 10 не подходит. Подбор можно сократить, не рассматривать все числа подряд, а проверять только числа, делящиеся на 5. Число 15 не подходит, так как не делится на 2. Так ученики доходят до числа 30, которое делится на 2, 3, 5 и не делится на 4. Значит, в корзине 30 яблок.

1. Условие или вопрос задачи можно разделить на части и решить задачу по частям.

Задача 7 . В два автобуса сели 123 экскурсанта. Затем из одного автобуса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали на машине. После этого в автобусах стало пассажиров поровну. Сколько пассажиров было в каждом автобусе сначала?

1) 8 – 3 =5 (чел.) – поехали на машине. 2) 123 – 5= 118 (чел.) – остались в каждом автобусе. 3) 118 : 2 = 59 (чел.) – стало в каждом автобусе. 4) 59 + 8 = 67 (чел.) - было в первом автобусе. 5) 59 - 3 = 56 (чел.) - было во втором автобусе.

Задача 8. 18 ручек стоят на 30 рублей больше, чем 30 карандашей. Те же 18 ручек стоят на 10 рублей больше, чем 40 таких же карандашей. Сколько стоят 1 карандаш и 1 ручка?

Разделить на части не условие, а вопрос задачи.

1. Решение задачи, начиная «с конца».

Задача 9. Мама дала детям конфеты: дочери половину всех конфет и ещё одну, сыну половину остатка и оставшиеся 5 конфет. Сколько всего конфет мама дала детям?

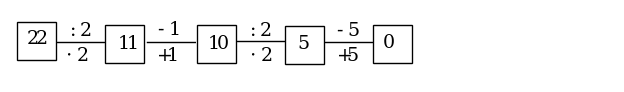
1. Решение задачи с помощью кругов Эйлера).

Задача 10. Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах.

Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб» и

«Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику.

Причем трем среди них нравятся еще и «Волк и теленок», шестерым - «Губка Боб

Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и

теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо

определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение

1) Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

2) Выходит, что:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

3) Осталось только разобраться, сколько шестиклассников предпочитает мультфильм «Губка Боб». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только мультфильм «Губка Боб».

Теперь можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб» выбрали 8 + 2 + 1 + 6 = 17 человек.

Это и есть ответ на поставленный в задаче вопрос.

Приемы работы с комбинаторными задачами

Учитель начальных классов

МБОУ СОШ №7

Алантьева Елена Николаевна

Комбинаторная задача – это задача, решение которой предполагает перебор всех возможных вариантов решения или подсчет их количества.

Способы решения комбинаторных задач делятся на две группы:

1) неформальные;

2) формальные.

Неформальный способ решения на первый план выводит сам процесс составления различных комбинаторных конфигураций. И главная его задача – быстро и правильно найти все возможные варианты.

К неформальным способам решения комбинаторных задач относят полный (непосредственный, хаотичный) перебор. Это самый элементарный способ, так как он не требует знания определений и формул. Поэтому именно его целесообразно использовать в начальной школе.

Сущность данного способа – перебрать, пересмотреть все возможные варианты и показать, что других быть не может. При этом важно, как организован процесс перебора, так как, если действовать случайным, хаотичным образом, то нельзя быть уверенным, что найдены все возможные комбинации. Чтобы избежать этого, нужно выполнять перебор по определенной системе, т.е. систематический перебор. Для этого используют комбинаторные таблицы, графы, «дерево решений».

Использование графа

По определению Н.Я. Виленкина, граф - это «множество, состоящее из конечного числа точек, некоторые пары которых соединены дугами (такие графы называются неориентированными; если вместо дуг используются стрелки, то получится ориентированный граф, или, орграф)».

A.M. Пышкало, Л.П.Стойлова, В.В.Рожденственская графом называют «особый чертеж, состоящий из точек и линий, идущих из одной точки в другую».

Задача 10: На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.

Решение: Вершины графа - это деревья, обозначенные первой буквой названия дерева. В данной задаче два отношения: ― «быть ниже» и ― «быть выше». Рассмотрим отношение ― «быть ниже» и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

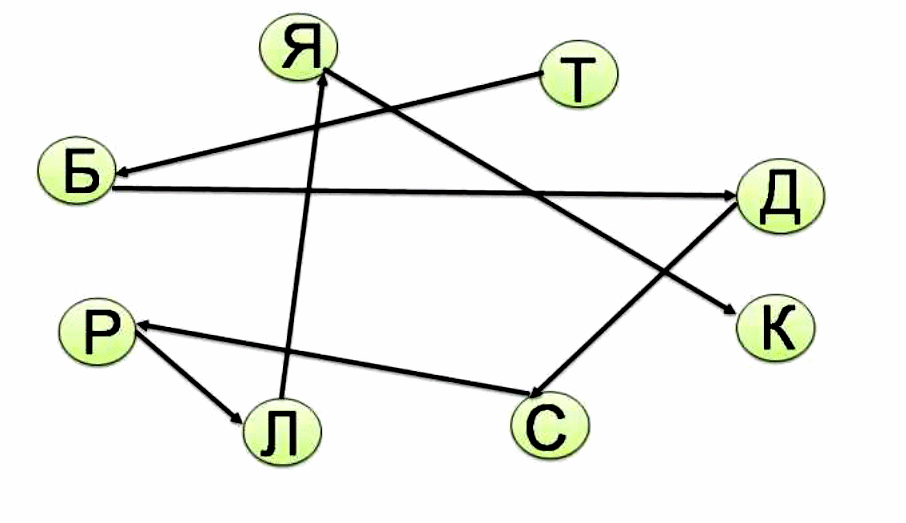Рис. 9

Ответ: клен, яблоня, лиственница, рябина, сосна, дуб, береза, тополь.

Задача 11: В парке 5 беседок. Было решено от каждой беседки ко всем остальным проложить дорожку. Продолжи рисунок, покажи, какие дорожки будут сделаны. Посчитай, сколько всего будет дорожек.

Решение:

Вершины графа - это беседки, обозначенные треугольниками (рис. 10).

Рассмотрим отношение между каждой беседкой. В задаче сказано, что нужно провести дорожки к каждой беседке. Продолжаем рисунок, проведя дорожки. Получаем граф, на котором видно сколько дорожек нужно провести.

Рис. 10

Ответ: 10 дорожек.

Использование таблицы

Решение комбинаторных задач можно выполнить и с помощью таблиц. Они схожи с деревом возможных вариантов, поскольку предлагают наглядное решение ситуации. Для нахождения правильного ответа нужно сформировать таблицу, причем она будет зеркальной: горизонтальные и вертикальные условия будут одинаковыми. Возможные варианты ответов будут получаться на пересечении столбцов и строчек. При этом ответы на пересечении столбца и строки с одинаковыми данными получаться не будут, эти пересечения необходимо особо пометить, чтобы не запутаться при составлении итогового ответа.

Задача 12: Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков.

Таблица 1

	Андрей	Миша	Игорь
Маша	Маша – Андрей	Маша - Миша	Маша – Игорь
Оля	Оля – Андрей	Оля – Миша	Оля – Игорь
Вера	Вера - Андрей	Вера – Миша	Вера – Игорь
Ира	Ира - Андрей	Ира - Миша	Ира - Игорь

Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы.

Задача 13: У Кати 6 карандашей и две коробки: синяя и красная. Как она может разложить карандаши в эти коробки? Сколько различных вариантов распределения карандашей по коробкам ты насчитал?

Таблица 2

Синяя коробка	0	1	2	3	4	5	6
Красная коробка	6	5	4	3	2	1	0

Решение: Задача решается методом систематического перебора.
Разложить карандаши можно так: в красную коробку положить все 6 карандашей, в синюю – ничего не класть; в красную положить 5 карандашей, в синюю – 1 и т.д.
Ответ: 7 вариантов.

Использование дерева выбора (вариантов)

Некоторые комбинаторные задачи можно решить, только составляя схемы, в которых будет подробно указана информация о каждом элементе. Составление дерева возможных вариантов – еще один способ нахождения ответа. Он подходит для решения не слишком-то сложных задач, в которых имеется дополнительное условие.

Задача 14: У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?

Решение:

Рис. 11

Ответ: 6 способов.

При формальном способе решения нужно определить характер выборки, выбрать соответствующую формулу или комбинаторный принцип подставить числа и вычислить результат. Результат - это количество возможных вариантов, сами же варианты в этом случае не образовываются. Основные комбинаторные правила: сложения, умножения.

Использование правила суммы

Пусть даны m действий x₁, x₂,, …, x_m таких, что выполнение любого из них не зависит от выполнения остальных действий. Если действие x1 можно выполнить k1 способами (i=1,2, …, m), тогда действие, состоящие в том, что выполняется одно любое из данных действий, можно выполнить k₁ + k₂ + … +k_m способами.

Задача 15. В вазе 6 белых цветов, 9 красных и 5 желтых. Сколькими способами можно взять из вазы один цветок?

Решение: Белый цветок можно выбрать 6 способами, красный - 9, жѐлтый – 5.На основании правила суммы заключаем, что или белый, или красный, или жёлтый цветок можно выбрать из вазы 6+9+5 способами.

Ответ. 20 способов.

Использование правила произведения

Если элемент x₁ можно выбрать k₁ способами, элемент x₂ – k₂ способами, …, элемент x_m - k_m способами, то набор (x₁, x₂, …, x_m) можно составить

k₁  k₂  …  k_m способами.

Задача 16. В магазине «Всё для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?

Решение: Чашку модем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6  4=24 способами (по правилу произведения).

Ответ: 24 способа.

Таким образом, для того, чтобы решить простую комбинаторную задачу, достаточно:

1) обозначить исходное множество, о котором идет речь в задаче; выяснить число его элементов;

2) определить тип выполняемой в задаче комбинаторной операции (упорядочивание, построение неупорядоченного подмножества, построение упорядоченного подмножества);

3) учитывая наличие или отсутствие повторения элементов в строящемся множестве, указать результат выполняемой комбинаторной операции;

4) подставить числовые данные в соответствующую формулу результата комбинаторной операции и вычислить ответ в задаче.

Для того, чтобы решить составную комбинаторную задачу, достаточно:

1) разбить исходную задачу на простые подзадачи и решить их с помощью сформулированного выше алгоритма;

2) ответить на вопрос исходной задачи, применив основные правила комбинаторики (правило суммы или правило произведения) к выделенным простым подзадачам.

Задачи на нахождение числа элементов в объединении и разности конечных множеств

Задача16. 25 учеников класса изучают английский язык, немецкий — 27 учеников, причем 18 школьников изучают одновременно оба языка. Сколько всего человек в классе изучают эти иностранные языки?» — лучше выполнить с помощью диаграммы Эйлера-Венна или отрезков.

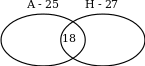
Рис. 12

Решение. Такая интерпретация условия задачи позволяет увидеть, что численное значение искомого не является суммой данных в тексте количеств учеников, изучающих какой-либо иностранный язык, поскольку число 18 содержится в этой сумме дважды. Поэтому для нахождения ответа на поставленный вопрос необходимо его удалить из полученного результата, т. е. решение задачи оформится выражением (25 + 27) – 18.

Ответ: 34 ученика в классе изучают эти иностранные языки.

Учитель начальных классов МБОУ СОШ мкр.Вынгапуровский Вербицкая Надежда Викторовна

Приемы работы по решению логических задач и задач на установление соответствия между элементами различных множеств

Логические задачи – это задачи, при решении которых поиск ответа на вопрос осуществляется на основе рассуждений. Вычисления при решении логических задач играют вспомогательную роль, а иногда совсем не нужны.

Различают следующие виды логических задач:

• с истинными и ложными высказываниями;

• на установление соответствия между множествами;

• на упорядочивание множества;

• на доказательство, основанное на выявлении худшего случая и с использованием принципа Дирихле;

• на планирование действий (взвешивания, переливания, переправы и др.)

Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач: способ рассуждений; способ таблиц; способ графов.

Охарактеризуем кратко эти способы.

Способ рассуждений - самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи

Задача17. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?

Решение. Имеется три утверждения:

1. Вадим изучает китайский;

2. Сергей не изучает китайский;

3. Михаил не изучает арабский.

Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.

Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.

Задачи на установление соответствия между элементами различных множеств

Рассмотрим задачи, содержащие конечные множества с одинаковым числом элементов, между которыми необходимо установить взаимно однозначное соответствие. Решению таких задач помогает использование таблиц или схем.

Задача 18. Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно, что один из нас русый, другой – брюнет, а третий – рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый из друзей?

Решение. В задаче рассматриваются два множества: множество друзей и множество цветов волос. Необходимо установить соответствие между элементами этих множеств. Очевидно, что соответствие является взаимно однозначным.

Для решения данной задачи воспользуемся таблицей. По условию задачи Белокуров не русый, Чернов не брюнет и Рыжов не рыжий. Поставим знак «-» в соответствующих ячейках таблицы. Кроме того, по условию, Белокуров – не брюнет, и, значит, на пересечении строки «Белокуров» и столбца «Черный» также поставим знак «-».

Таблица 3

Цвет Фамилия	рыжие	чёрные	русые
Белокуров		-	-
Чернов		-
Рыжов			-

С помощью таблицы можно сделать вывод, что Белокуров имеет рыжий цвет волос. Поставим знак плюс в соответствующей ячейке. Отсюда видно, что цвет волос Чернова не рыжий. Обозначим это знаком минус в таблице. Следовательно, Чернов может быть только русым, а Рыжов – брюнетом.

Таблица 4

Цвет Фамилия	рыжие	чёрные	русые
Белокуров	+	-	-
Чернов	-	-	+
Рыжов	-	+	-

Представим другое решение данной задачи с помощью ее графической модели (рис. 12). При этом элементы различных множеств обозначаются

точками, а соответствия между ними – отрезками. Пунктирные линии будут обозначать указанное в задаче отсутствие соответствия.

Пунктирными линиями соединим пары: Чернов – черные, Белокуров – русые, Рыжов – рыжие и Белокуров – черные.

Рис. 13

Тогда, рассуждая аналогично табличному способу решения, мы соединим сплошными линиями: Белокуров – рыжие, затем Чернов – русые и, наконец, Рыжов – черные.

Рассмотрим еще один тип логических задач. Это задачи на переливания, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости. Такие задачи можно решить методом перебора всевозможных вариантов, но в этом случае трудно удержать в памяти все звенья логических рассуждений.

Задача 19. Как, имея два сосуда ёмкостью 3л и 5л, набрать из водопроводного крана 4 л воды?

Решение. Начнём с конца. Как в результате может получиться 4 литра воды?
Из 5 – литрового сосуда отлить 1 л.

Как это сделать?
Надо в 3 – литровом сосуде иметь ровно 2 л.
Как их получить?
Из 5 – литрового сосуда отлить 3л. Теперь запишем решение задачи сначала в виде таблицы. Таблица 5

ХОДЫ	1	2	3	4	5	6
5 л	5	2	2	-	5	4
3 Л	-	3	-	2	2	3

Поиск решения можно было начать с действия 3+1,что привело бы к решению, записанному в следующей таблице.

Таблица 6

ХОДЫ	1	2	3	4	5	6	7	8
5 л	-	3	3	5	-	1	1	4
3 Л	3	-	3	1	1	-	3	1

Из чисел 3 и 5 можно составить выражения, имеющие значение 4:

5-3+5-3=4 и 3+3-5+3= 4

Несложно убедиться, что полученные выражения соответствуют найденным выше решениям!

Задачи на переливания удобнее решать способом блок-схем, в котором используются условные команды. Рассмотрим этот метод подробнее. Для начала введем сокращенные обозначения для операций, которые могут быть использованы: НБ – наполнить больший сосуд; ОМ – опустошить меньший сосуд; Б→М – перелить из большего сосуда в меньший, пока больший сосуд не опустеет или меньший не наполнится. Кроме этих трех операций введем сокращенные обозначения и для условий, которые будут использоваться в блок-схеме: Б=0? – посмотреть, пуст ли больший сосуд; МН? — посмотреть, наполнен ли малый сосуд.
 Изобразим последовательность команд в виде блок-схемы.

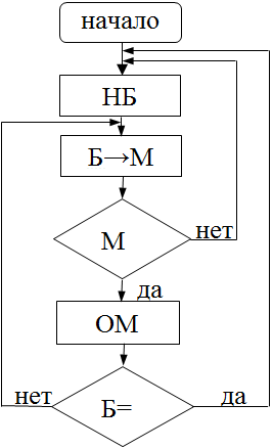
Рис.14
Последовательность переливаний, изображенная на блок-схеме следующая: сначала наполняется больший сосуд, затем вода из большего сосуда переливается в меньший. Всякий раз, когда меньший сосуд наполняется, он опустошается, и всякий раз, когда больший сосуд опустошается, он заново наполняется.
  Решим методом блок-схем следующую задачу: имеются два сосуда – трехлитровый и пятилитровый, нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
Решение. Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной блок-схеме. Результаты оформим в виде таблицы.

Таблица 7

ТАБЛИЦА ПЕРЕЛИВАНИЙ
5 л	0	5	2	2	0	5	4	4	1	1	0	5	3	3	0	0
3 л	0	0	3	0	2	2	3	0	3	0	1	1	3	0	3	0
3 л + 5 л	0	5	5	2	2	7	7	4	4	1	1	6	6	3	3	0

Дальше эта последовательность будет полностью повторяться. Из таблицы видно, что количество воды в обоих сосудах вместе образует следующую последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по приведенной схеме, можно отмерить любое количество литров от 1 до 7. Чтобы отмерить еще и 8 литров, надо наполнить оба сосуда.
 Если сначала наполнить меньший сосуд, то блок-схема, изображающая последовательность переливаний, будет выглядеть следующим образом (обозначения аналогичные):

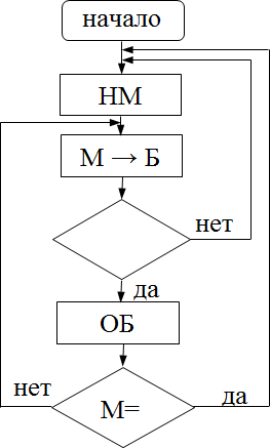
Рис.15

Идея способа: описать последовательность выполнения операций, определить порядок их выполнения и фиксировать состояния.

Список литературы:

1. Артемов А. К. Теоретико-методические особенности поиска способов решения математических задач. // Начальная школа. 1998 № 12 с.48-53.

2. Бантова М. А., Бельтюкова Т. В. Методика преподавания математики в начальных классах. - М.: Просвещение, 1984 -335 с.

3. Бантова М. А. Методика преподавания математики в начальных классах. М. «Прорсвещение» 1976 г.

4. Беспалько В. Л. Программированное обучение. - М. 1970.

5. Гришкова В. Н. Памятка «Как работать над задачей». // Начальная школа. 2004, №1, с. 68.

6. Глушков И. К. Дифференцированная работа над задачами. // Начальная школа. 1986, №2, с. 34-35.

7. Давыдов В. В., Теория развивающего обучения. - М.: Интор 1996., 544 с.

8. Истомина Н. Б. методика обучения математике в начальных классах. – М.: Академия, 2000, 288 с.

9. Истомина Н. Б. Обучение решению задач. // Начальная школа, 1998, №12

10. Истомина Н. Б. Работа над составной задачей. // Начальная школа, 1998, №2, с.44-49.

11. Истомина Н. Б., Нефедова И. Б. Первые шаги в формировании умения решать задачи. // Начальная школа, 1998, №11, с. 42-48.

12. Кожухов С. Составление задач школьниками. // Математика в школе, 1995, №2, с. 4-6.

13. Лопатников Л. И. Экономико-математический словарь: Словарь современной экономической науки. - 5-е изд. - М.: Дело, 2003

14. Мамыкина М. Ю. Работа на задачей. // Начальная школа, 2003, №4, с. 63-67.

15. Моро М. И., Пышкало А.М. Методика обучения математике 1-3 классах. - М.: Просвещение, 1978, 336 с.

16. Матвеева Н. А. Методические приемы обучения составлению задач. // Начальная школа, 2003, №6, с. 41.

17. Ожегов С. И. Словарь русского языка. - М.: Русский язык, 1990 - 943 с.

18. Петровский А. В., Ярошевский М. Г., Психология. Словарь. - М.: Изд. полит, лит. 1990 - 495 с.

19. Попова Н. С. Методика преподавания арифметики в начальной школе. - Ленинград, 1955.

20. Рубинштейн С. Л. Основы общей психологии: в 2т. – М. 1989, 328 с.

21. Скаткин Л. Н. Обучение решению простых и составных задач. М., 1963, 183с.

22. Сохор А. М. Логическая структура учебного материала. Вопросы дидактического анализа. - М, 1974.

23. Туркина В. М. Задачи в 1 классе. // Начальная школа, 1996, №9, с. 51-53

24. Уткина Н. Г., Улитина Н. В. Сборник упражнений и работ по математике для начальной школы. – М. Аркти-ларгос, 1997 г.

25. Ушаков Д. Н. Большой толковый словарь современного русского языка. - М.: Альта-принт, 2005 г.

26. Фридман Л. М. Логико-психологический анализ школьных учебных задач. – М.: Просвещение. 1997г., 208 с.

27. Халидов М. М., Мукина В. М. Теория и практика обучения младших школьников решению математических задач. // Начальная школа, 2006 №9, с 54.

28. Царева С. Е. Виды работы с задачами на уроке математики. // Начальная школа. 1990, №10, с.37-41.

29. Царева С. Е. Непростые простые задачи. // Начальная школа. 2005, №1, с.49.

30. Царева С. Е. Нестандартные виды работы с задачами на уроке как средство реализации современных педагогических концепций и технологий. // Начальная школа. 2004, №7, с.45.

31. Царева С. Е. Обучение решению задач. // Начальная школа. 1998 №1. с. 102-107.

32. Царева С. Е. Обучение решению текстовых задач, ориентированное на формирование учебной деятельности младших школьников. - Новосибирск: НГПУ, 1988, 136 с.

33. Царева С. Е. Обучение составлению задач. // Начальная школа, 1997, №11, с. 93.

34. Целищева И. И. Обучение решению задач детей 4-10 лет. // Начальная школа. 2005, №11, с.83

35. Чекмарёв Я. Ф. Методика преподавания арифметики в 5-6 классах. – М., 1962.

36. Шикова Р. Н. Работа над текстовыми задачами. // Начальная школа. 1991, №5, с.22-27.

37. Шмырева Г. Г. Работа со схемой в ходе подготовки к решению задач. // Начальная школа, 2007, №8, с.46.

38. Шорникова И. В. Некоторые виды работ по преобразованию задач. // Начальная школа. 1991, №11, с 21-23.

39. Эрдниев П. М. и Эрдниев Б. П. Теория и методика обучения математике в начальной школе. – М.: Педагогика, 1998, 220 с.

56