

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Дидактический материал по Геометрии 11 класс.
Набор контрольно-измерительных материалов по геометрии для 11 класса. Включает в себя: математические диктанты, самостоятельные работы, решение задач по готовым чертежам, тематические тесты, зачеты, контрольные работы.
Просмотр содержимого документа
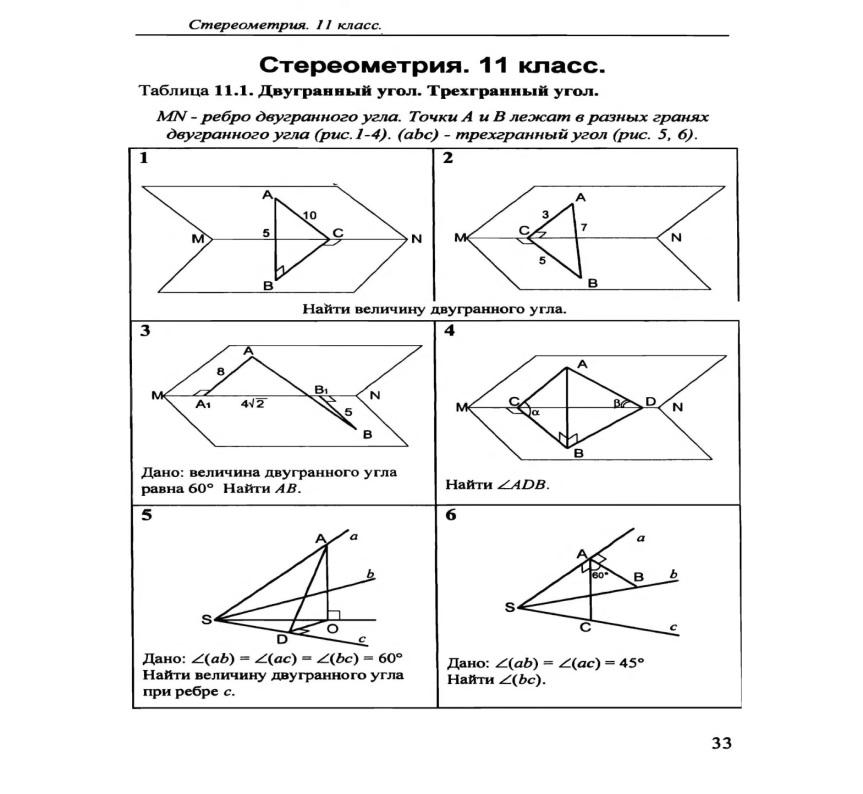
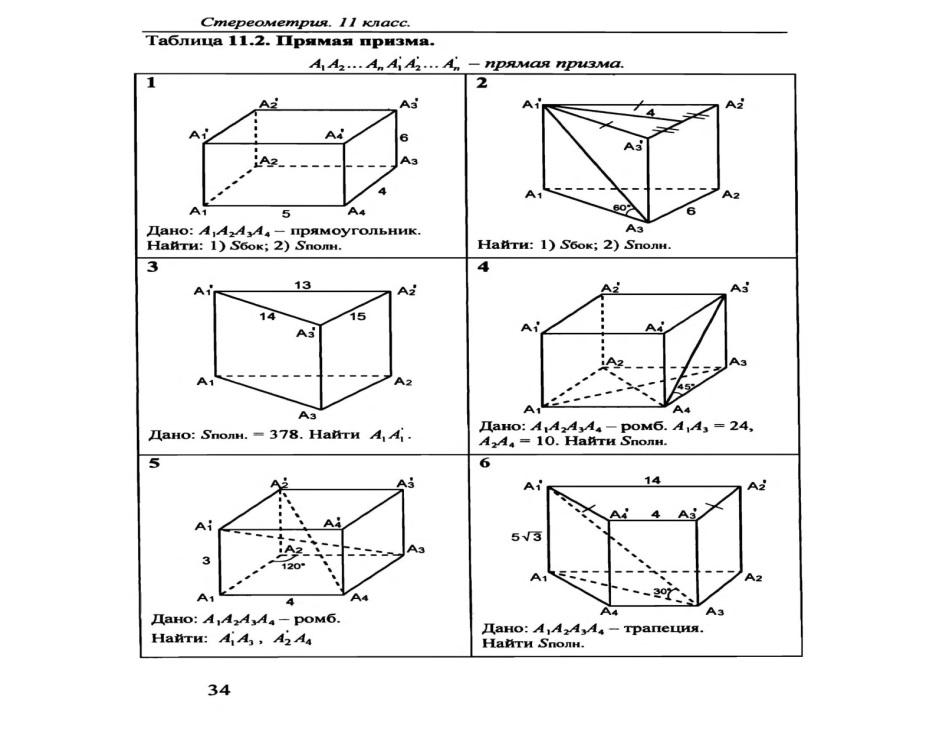
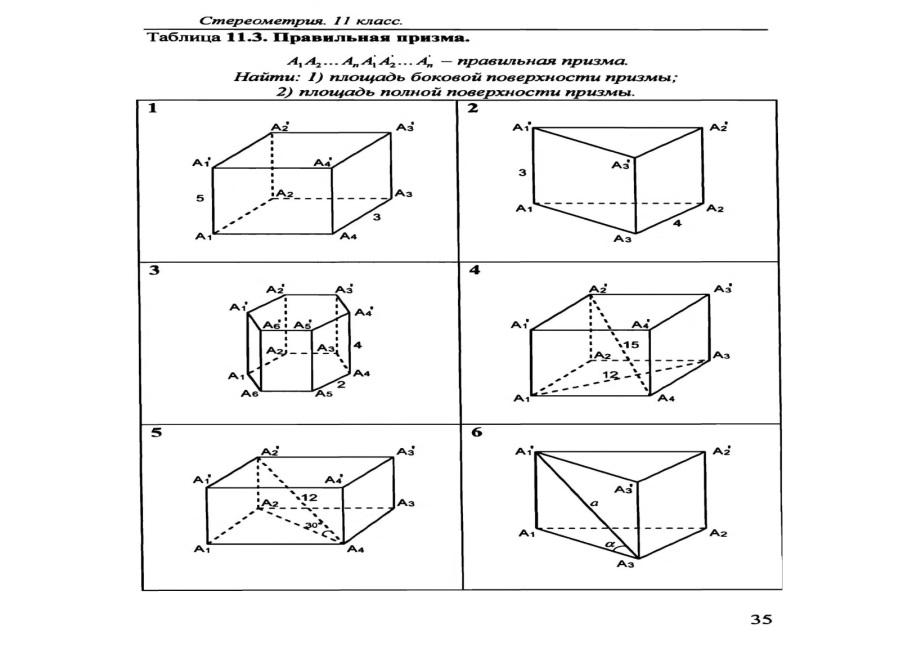
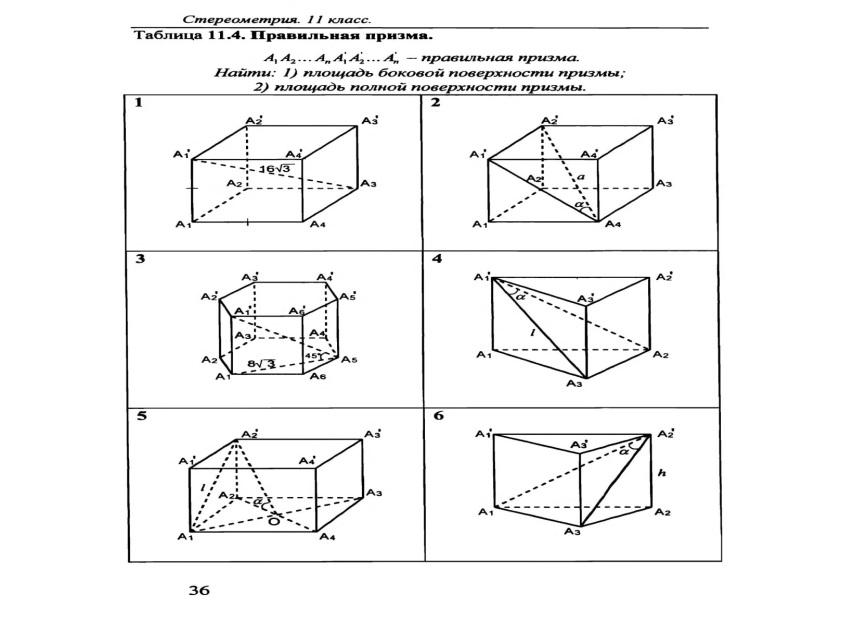
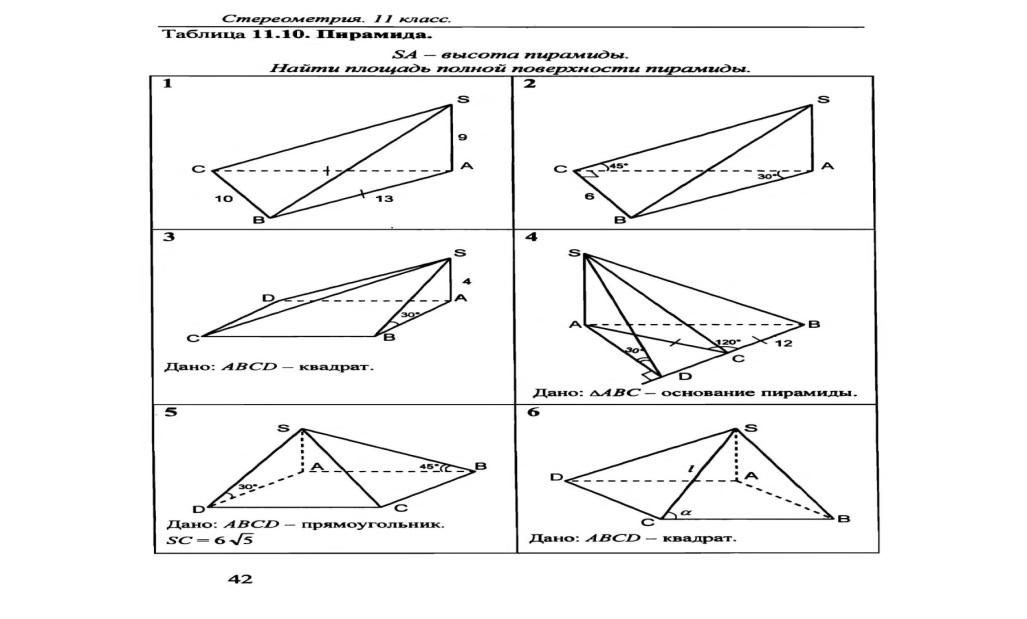
«Задачи по готовым чертежам 11 кл»



Просмотр содержимого документа
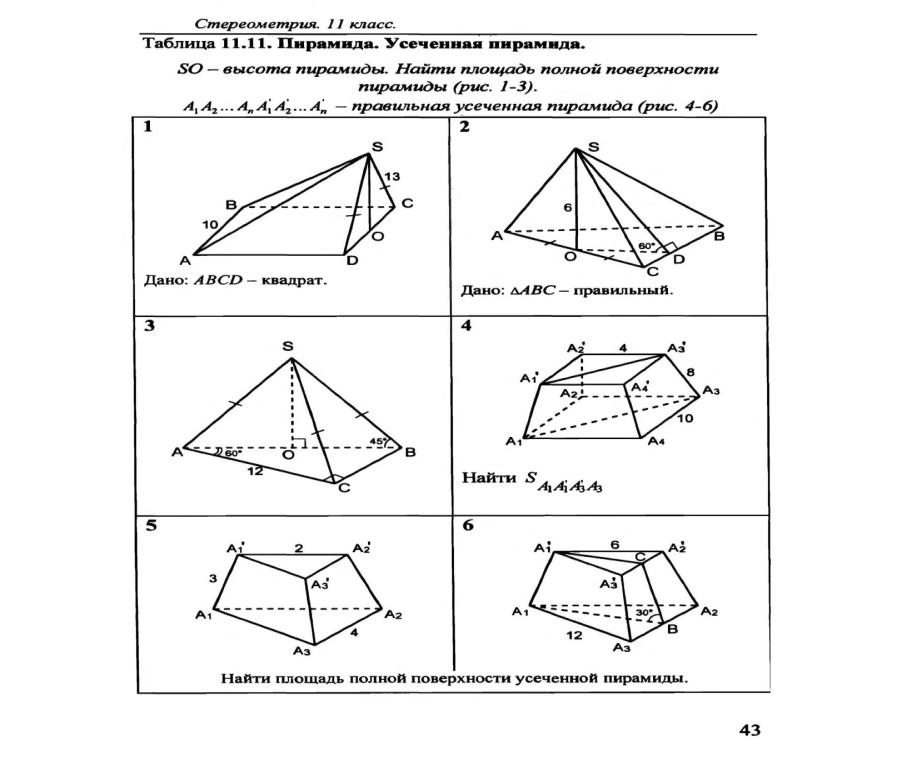
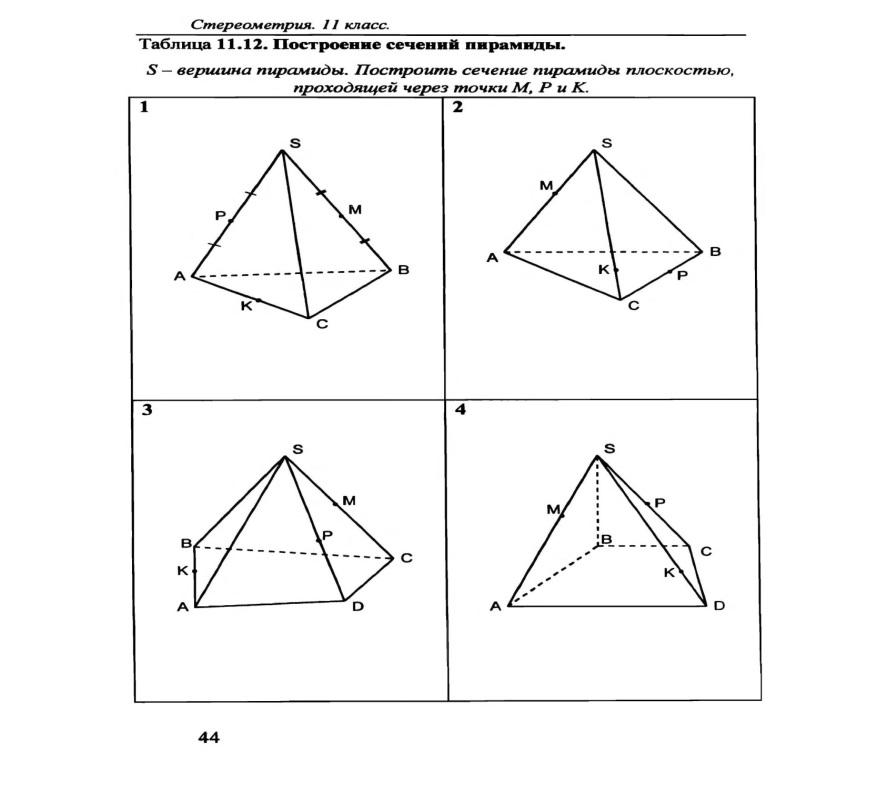
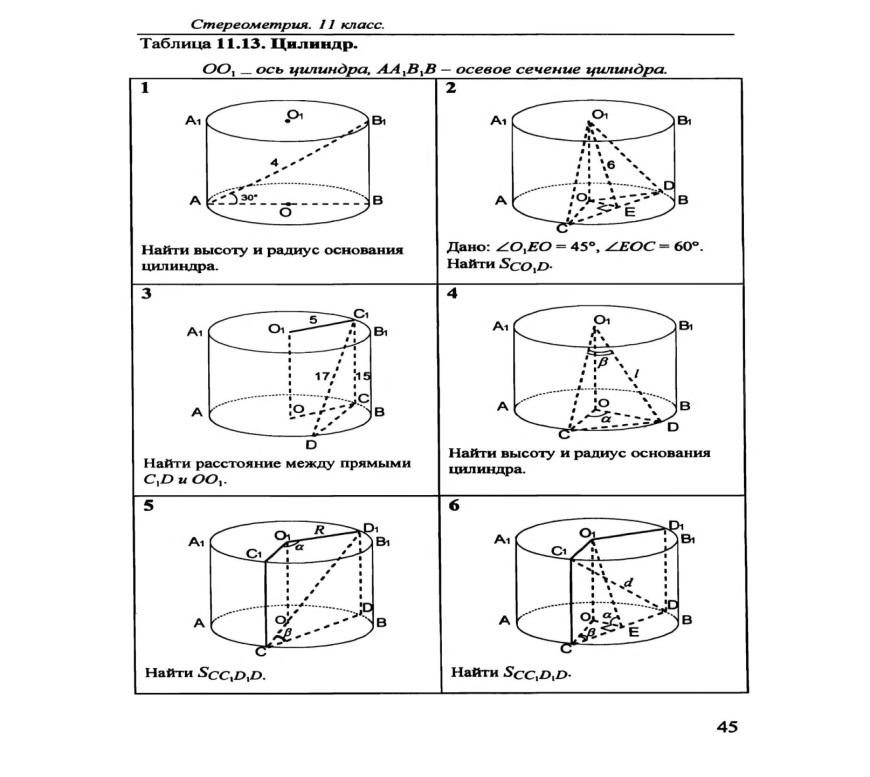
«Зачеты 11 кл»
Зачёт по геометрии 11 кл.
Тема : Метод координат в пространстве.
Карточка №1
Расскажите, как задаётся прямоугольная система координат в пространстве и как определяются координаты вектора.
Запишите формулы выражающие координаты середины отрезка через координаты его концов.
Дан куб ABCDA1 B1 C1 D1. Вычислите угол между векторами ВD и CB.
Зачёт по геометрии 11 кл.
Тема : Метод координат в пространстве.
Карточка №2
1.Расскажите о связи между координатами векторов и координатами точек.
2. Запишите формулы выражающие координаты середины отрезка через координаты его концов.
3. Вычислите угол между прямыми АВ и СD, если А(1;1;0), В (3;-1; 0), С(4; -1;2), D (0;1;0)
Зачёт по геометрии 11 кл.
Тема : Метод координат в пространстве.
Карточка №3
Сформулируйте определение скалярного произведения двух векторов. Сформулируйте условие перпендикулярности двух ненулевых векторов, используя скалярное произведение.
Запишите формулу для вычисления длины вектора по его координатам.
Даны точки А(0;4;0), В (2;0;0), С(4;0;4), D(2;4;4). Докажите, что АВСD - ромб.
Зачёт по геометрии 11 кл.
Тема : Метод координат в пространстве.
Карточка №4
1.Сформулируйте основные свойства скалярного произведения векторов.
2. Запишите формулу для вычисления расстояния между двумя точками с заданными координатами.
3. Даны координаты трёх вершин параллелограмма АВСD : А(-6;-4; 0), В(6; -6;2), С(10;0;4). Найдите координаты точки D и угол между векторами АС и ВD.
Зачёт по геометрии 11 кл.
Тема : Метод координат в пространстве.
Карточка №5
1.Дать определение движения пространства. Приведите примеры движения.
2. Запишите формулу косинуса угла между ненулевыми векторами с заданными координатами.
3. Даны векторы а 1;2;-1 b -3; 1; 4 c 3; 4 ;-2 d 2 ;-1; 3 . вычислите скалярное произведение ( a + 2b) ( c-d).
Зачёт по геометрии 11 кл.
Тема : Метод координат в пространстве.
Карточка №6
Назвать виды движения.
Как вычислить угол между двумя прямыми в пространстве с помощью направляющих векторов этих прямых.
Вычислите косинус угла между прямыми АВ и СD если: А (7; -8;15), В (8; -7; 13), С (2; -3; 5) D(-1; 0; 4).
Зачёт по теме «Метод координат в пространстве. Движения».
Работу выполнил(а)________________________________________________.
В прямоугольной системе координат оси носят названия: Ох - ________________________
Оу - ____________________________, Оz - ________________________________________.
Какие координаты имеет точка А, если она лежит на оси ординат?____________________
Какие координаты имеет точка В, если она лежит в плоскости Оxz?___________________
Каждая координата суммы двух или более векторов равна___________________________
Радиус-вектором данной точки называется _________________________________________
Координаты ________________________________ равны соответствующим координатам её радиус-вектора.
Каждая координата середины отрезка равна ________________________________________
Вычисление длины вектора
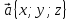 производится по формуле _______________________.
производится по формуле _______________________.Может ли одна из координат вектора равняться 7, если длина этого вектора равна 5? _____
Запишите формулу для вычисления расстояния между точками А

_____________________________________________________________________________
Чтобы найти координаты вектора надо ___________________________________________
Запишите формулу скалярного произведения векторов
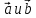
а) в длинах:_________________________________________________________________
б) в координатах:____________________________________________________________
Когда скалярное произведение равно 0?___________________________________________.
Когда скалярное произведение отрицательно?______________________________________.
Запишите формулу для нахождения косинуса угла между ненулевыми векторами:
Когда ненулевой вектор называется направляющим?________________________________
Движение пространства – это____________________________________________________
_______________________________________________________________________
Зачёт №1
«Метод координат в пространстве»
Вариант 1
Даны точки А(5; 0; 2), В(4; -3; 2),
С(0; 0; 1), D(2; -4; -4). Найдите:

 а) координаты векторов АВ и СD;
а) координаты векторов АВ и СD;


 б) координаты векторов а = АВ + СD,
б) координаты векторов а = АВ + СD,




 b = AB – CD, с = -⅓АВ;
b = AB – CD, с = -⅓АВ;

 в) длины векторов а и b;
в) длины векторов а и b;
г) скалярное произведение векторов



 АВ и СD, а и b.
АВ и СD, а и b.
2. Вершины треугольника КМN имеют координаты K(-2; 3; -2), M(8; 1;2), N(2; -3; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
Зачёт №1
«Метод координат в пространстве»
Вариант 2
Даны точки А(5; -5; 0), В(-2; 1; -3),
С(0; 3; 1), D(1; 3; -4). Найдите:

 а) координаты векторов АВ и СD;
а) координаты векторов АВ и СD;


 б) координаты векторов а = АВ + СD,
б) координаты векторов а = АВ + СD,




 b = AB – CD, с = ⅓АВ;
b = AB – CD, с = ⅓АВ;

 в) длины векторов а и b;
в) длины векторов а и b;
г) скалярное произведение векторов



 АВ и СD, а и b.
АВ и СD, а и b.
2. Вершины треугольника КМN имеют координаты K(8; 3; 5), M(14; 1;0), N(12; -5; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
Урок 30 Геом. 11 кл
Зачет по карточкам
№1
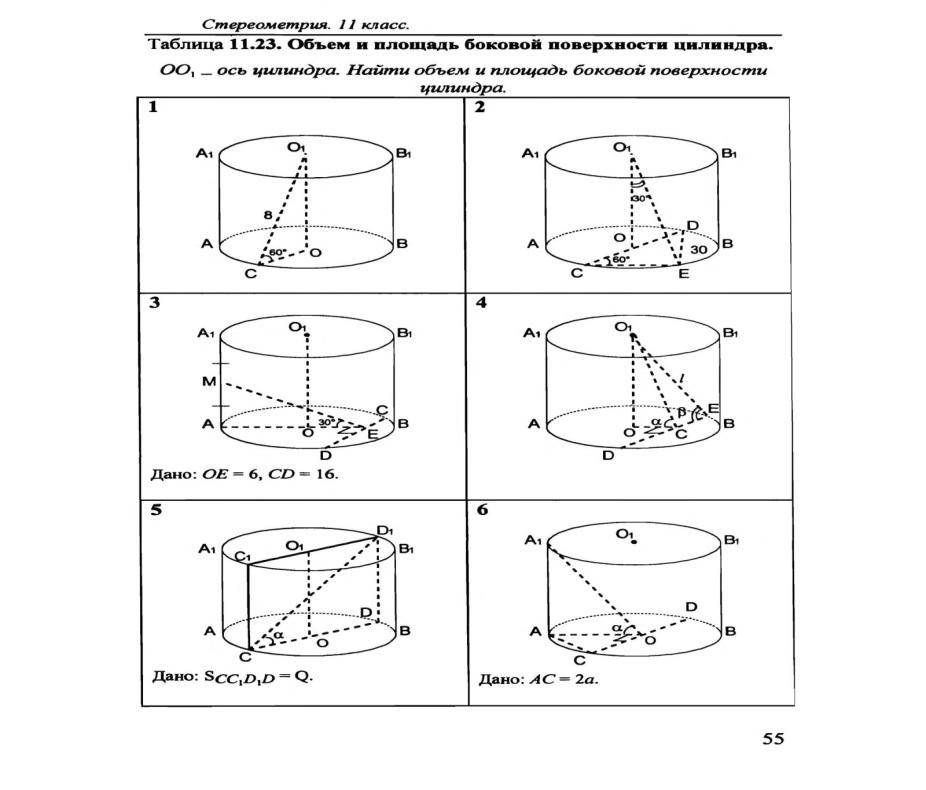
1.Объясните , какое тело называется цилиндром
2. Какая фигура образуются при вращении треугольника АВС вокруг оси ( достроить). Вычислите полную поверхность тела вращения, которое получается в результате вращения треугольника АВС вокруг его стороны АС, если АС=8см, ВС=5см.
3. Высота конуса равна 6см, а образующая наклонена к плоскости основания под углом в 30 . Найдите площадь сечения конуса плоскостью , проходящей через две образующие , угол между которыми равен 60.
4. Радиус шара равен R . Найдите площадь поверхности вписанного в шар куба.
Урок 30 Геом. 11 кл
Зачет по карточкам
№2
1.Объясните ,какое тело называется конусом .
2. Вычислите полную поверхность тела вращения , которое получается в результате вращения треугольника АВС вокруг его стороны АВ, если АВ=4см, ВС=3см.
3. Радиус шара равен 8см. Через конец радиуса , лежащего на сфере , проведена плоскость под углом 45 к радиусу . Найдите площадь сечения шара этой плоскостью.
4. Куб с ребром а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.
Многогранники и площади их поверхностей
Подготовка к зачету
Вопросы
1. Назовите элементы многогранника и дайте их определения.
2. Что называется основанием боковой гранью, ребром призмы?
3. Какая призма называется прямой (наклонной)?
4. Какая призма называется правильной?
5. Что принимается за боковую (полную) поверхность призмы?
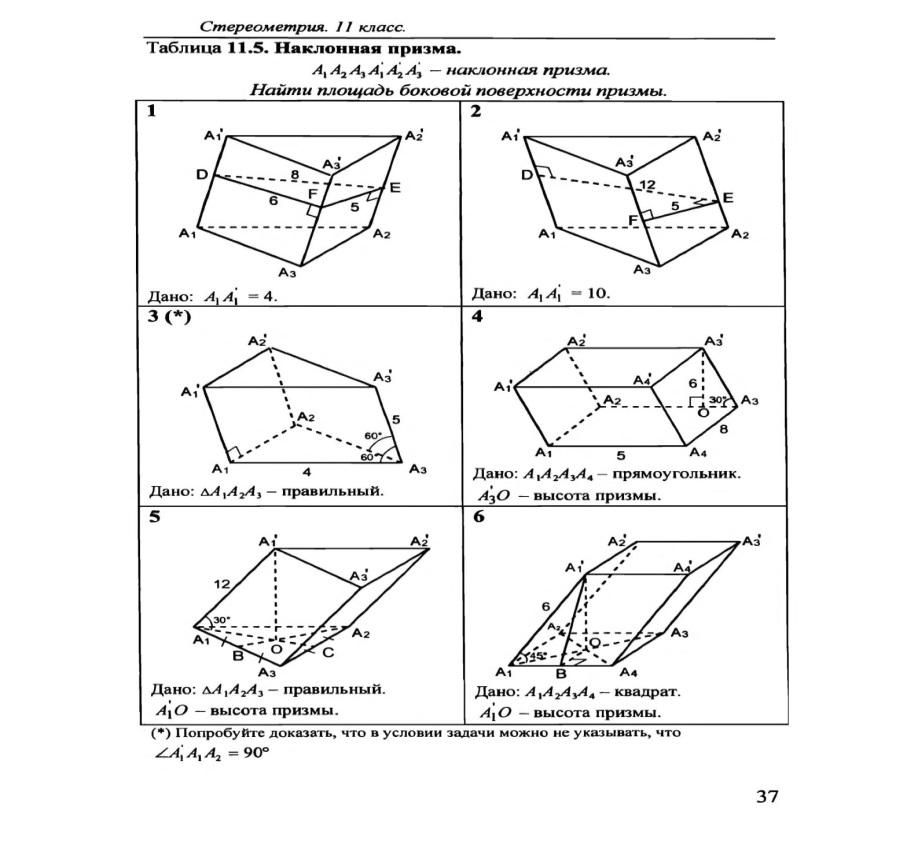
6. Докажите, что площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
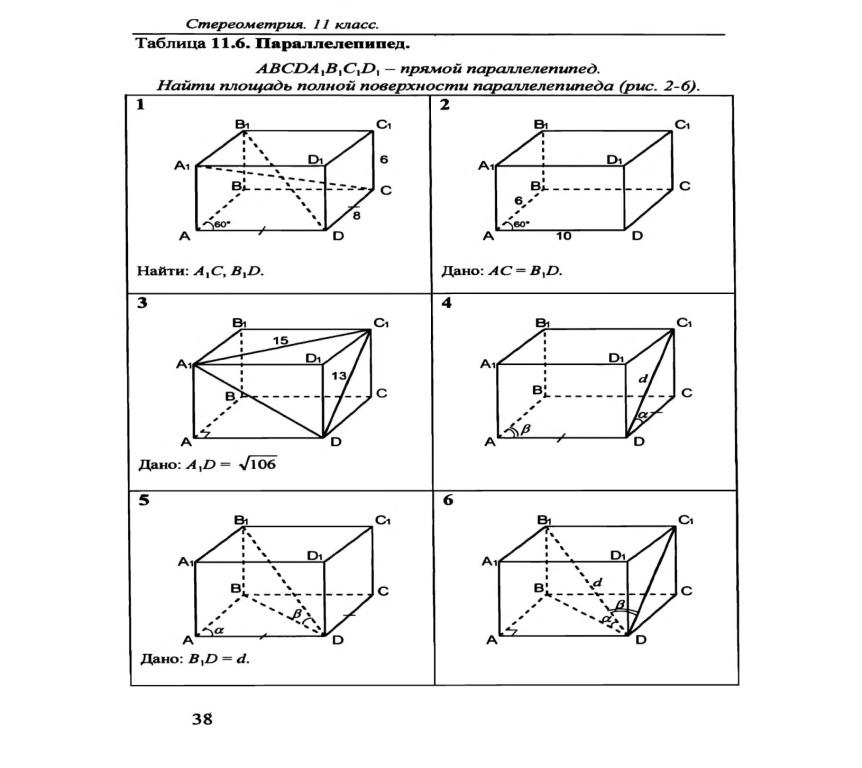
7. Какой многогранник называется параллелепипедом?
8. Докажите, что у параллелепипеда противоположные грани равны и параллельны.
9. Докажите, что диагонали параллелепипеда пересекаются в одной точке и делятся точкой пересечения пополам.
10. Докажите, что в прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.
11. Какой параллелепипед называется прямоугольным?
12. Что такое куб?
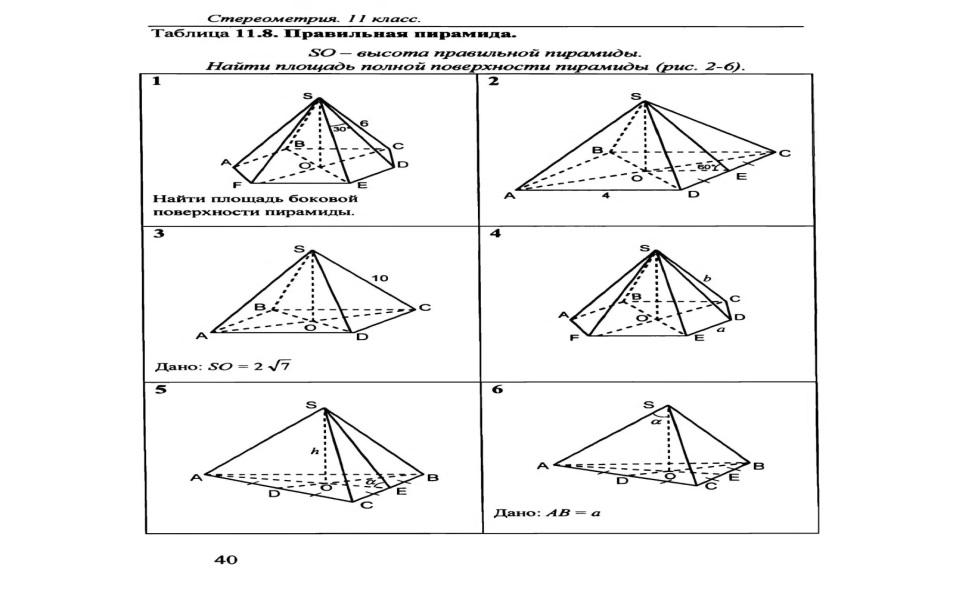
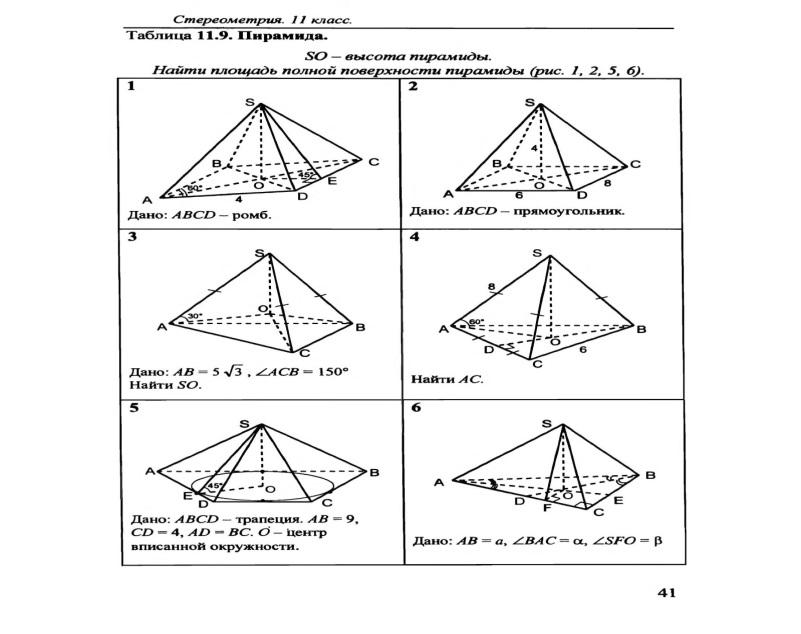
13. Назовите элементы пирамиды и дайте их определения.
14. Какая пирамида называется правильной?
15. Докажите, что площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
16. Докажите, что площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
17. Дайте определение тетраэдра. Какое наименьшее число ребер (граней, вершин) имеет многогранник?
18. Какие многогранники называются правильными? Перечислите известные вам виды правильных многогранников.
19. Докажите, что у прямой призмы все боковые грани - прямоугольники.
20. В пирамиде все боковые грани равны между собой. Докажите, что высота пирамиды проходит через центр окружности, описанной около основания.
21. В пирамиде все боковые ребра равны между собой. Докажите, что они составляют с плоскостью основания равные углы.
22. Докажите, что у правильной призмы все боковые грани - равные прямоугольники.
Задания к зачету
КАРТОЧКА 1
1. Нарисуйте многогранник. Что является основанием и боковыми гранями многогранника? Назовите элементы многогранника и дайте их определения. Ответ поясните рисунком.
2. Почему все высоты призмы равны между собой? Ответ обоснуйте.
3. а) Запишите формулу площади боковой поверхности правильной пирамиды.
б) Выведите формулу для п. а).
КАРТОЧКА 2
1. Сколько вершин, граней, ребер имеет шестиугольная призма? Ответ поясните на модели призмы.
2. Дан прямоугольный параллелепипед  с высотой
с высотой 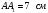 . Найдите величину двугранного угла
. Найдите величину двугранного угла 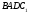 , если четырехугольник
, если четырехугольник 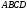 - квадрат со стороной
- квадрат со стороной  .
.
3. а) Каким свойством обладают противоположные грани параллелепипеда?
б) Докажите свойство, сформулированное в п. а).
КАРТОЧКА 3
1. Дайте определение тетраэдра. Какое наименьшее число ребер (граней, вершин) имеет многогранник?
2. В основании пирамиды лежит семиугольник. Сколько граней, вершин, ребер, апофем имеет эта пирамида? Ответ поясните рисунком.
3. а) Запишите формулу площади боковой поверхности правильной треугольной пирамиды, у которой сторона основания  , боковое ребро
, боковое ребро 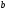 .
.
б) Выведите формулу для п. а).
КАРТОЧКА 4
1. Нарисуйте призму, назовите ее элементы. Что является основанием, боковыми гранями призмы?
2. Боковое ребро пирамиды перпендикулярно одной из сторон основания. Можно ли принять это ребро за высоту пирамиды? Ответ поясните рисунком и обоснуйте.
3. а) Каким свойством обладают диагонали параллелепипеда?
б) Докажите свойство, сформулированное в п. а).
КАРТОЧКА 5
1. Что называется основанием, боковой гранью пятиугольной призмы? Ответ поясните рисунком.
2. Основанием треугольной пирамиды является равносторонний треугольник. Одна из ее боковых граней перпендикулярна плоскости основания. Является ли данная пирамида правильной? Ответ поясните рисунком и обоснуйте.
3. а) Запишите формулу площади боковой поверхности прямой призмы.
б) Выведите формулу для п. а).
КАРТОЧКА 6
1. Какая призма является прямой (наклонной). Ответ поясните рисунком.
2. Дан прямой параллелепипед 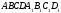 , в основании которого лежит ромб с углом
, в основании которого лежит ромб с углом 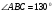 . Выпишите большие диагонали параллелепипеда. Ответ обоснуйте.
. Выпишите большие диагонали параллелепипеда. Ответ обоснуйте.
3. а) Запишите формулу площади боковой поверхности наклонной призмы.
б) Выведите, формулу для п. а).
КАРТОЧКА 7
1. Какой параллелепипед называется прямоугольным? Ответ поясните рисунком.
2. Призма имеет 20 граней. Какой многоугольник лежит в ее основание? Сколько вершин и ребер имеет эта призма?
3. а) Что принимается за площадь боковой поверки правильной усеченной пирамиды?
б) Выведите формулу для п. а).
КАРТОЧКА 8
1. Какая призма называется правильной? Ответ поясните рисунком.
2. Сколько граней, ребер, вершин имеет пятиугольная пирамида? Ответ поясните рисунком.
3. а) Сформулируйте утверждение о высоте пирамиды, в которой все боковые ребра равны между собой.
б) Докажите утверждение п. а).
КАРТОЧКА 9
1. Какая призма называется параллелепипедом? Ответ поясните рисунком.
2. Сколько плоскостей симметрии можно провести через вершину правильного тетраэдра? Ответ поясните рисунком.
3. а) Чему равен квадрат любой диагонали прямоугольного параллелепипеда?
б) Докажите теорему о квадрате диагонали правильного параллелепипеда.
КАРТОЧКА 10
1. Всякий ли параллелограмм может быть основанием правильного параллелепипеда? Ответ обоснуйте.
2. В правильной треугольной пирамиде проведено сечение через ее высоту и апофему. Как расположена плоскость сечения по отношению к стороне основания? Ответ поясните рисунком и обоснуйте.
Ответ: плоскость сечения перпендикулярна плоскости основания согласно признаку перпендикулярности двух плоскостей.
3. а) Что принимается за площадь полной поверхности правильного тетраэдра?
б) Выведите формулу для п. а).
3. а) Докажите, что боковые грани прямой призмы - прямоугольники.
б) Можно ли утверждать, что боковые грани правильной призмы равны? Ответ обоснуйте.
б) плиток, требуемых для облицовки стен операционной комнаты;
в) материала, идущего на покрытие купола Московского цирка на Цветном бульваре?
Ответ обоснуйте.
3. а) Что принимается за площадь полной поверхности прямоугольного параллелепипеда?
б) Выведите формулу для п. а).
*Фриз - окрашиваемая поверхность стен между потолком и гобеленом или между потолком и панелью (при отсутствии гобелена) с минимальной высотой 50 мм.
КАРТОЧКА 11
1. Сколько плоскостей симметрии имеет правильная четырехугольная пирамида?
2. Дан наклонный параллелепипед 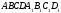 . Известно, что угол основания,
. Известно, что угол основания, 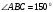 . Какое из диагональных сечений параллелепипеда больше? Ответ поясните рисунком и обоснуйте.
. Какое из диагональных сечений параллелепипеда больше? Ответ поясните рисунком и обоснуйте.
3. а) Как найти площадь полной поверхности правильной четырехугольной призмы, не применяя формулу?
б) Выведите формулу для п. а).
КАРТОЧКА 12
1. Сколько центров симметрии имеет параллелепипед? Ответ поясните рисунком.
2. Будет ли сечение, перпендикулярное боковому ребру призмы, перпендикулярно ее боковой грани? Ответ обоснуйте.
3. а) Запишите формулу для площади полной поверхности куба по его ребру  .
.
б) Выведите формулу полной поверхности куба, зная его диагональ 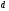 .
.
КАРТОЧКА 13
1. Какая призма называется кубом? Ответ поясните рисунком.
2. Дана правильная треугольная пирамида. Можно ли утверждать, что ее апофемы равны? Ответ обоснуйте.
3. а) Что принимается за площадь боковой поверхности правильной шестиугольной призмы?
б) Выведите формулу для п. а).
Тела вращения и площади их поверхностей
Подготовка к зачету
Вопросы
1. Что такое боковая поверхность основания, образующие, ось, радиус и высота цилиндра?
2. Что представляет собой сечение цилиндра, если секущая плоскость проходит через ось цилиндра? Как называется такое сечение?
3. Объясните, что такое развертка боковой поверхности цилиндра. Что принимается за площадь боковой поверхности цилиндра?
4. Докажите, что площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
5. Что называется площадью полной поверхности цилиндра? Как ее вычислить, если даны радиус и высота цилиндра?
6. Что такое боковая поверхность, основание, образующие ось и высота конуса?
7. Что представляет собой осевое сечение конуса? Как называется такое сечение?
8. Что представляет собой сечение конуса плоскостью, перпендикулярной оси конуса?
9. Объясните, что представляет собой развертка боковой поверхности конуса. Что принимается за площадь боковой поверхности конуса?
10. Докажите, что площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
11. Что принимается за площадь полной поверхности конуса? Как ее вычислить, если даны радиус основания и образующая?
12. Что такое боковая поверхность, основания, образующие усеченного конуса?
13. Докажите, что площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.
14. Что называется сферой или шаровой поверхностью?
15. Какое тело называется шаром? Что такое центр, радиус, диаметр шара?
16. Что представляет собой сечение шара плоскостью? Что такое большой круг шара?
17. Докажите, что пересечение шара плоскостью есть круг.
18. Что такое касательная плоскость к сфере? Какая точка называется точкой касания сферы и плоскости?
19. Докажите, что плоскость имеет с шаром только одну общую точку - точку касания.
20. Какая прямая называется касательной к шару?
21. Докажите, что через любую точку шаровой поверхности проходит бесконечное множество касательных прямых, причем все они лежат в касательной плоскости шара.
22. Выведите уравнение сферы данного радиуса с центром в точке с данными координатами.
23. Исследуйте взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.
24. Докажите, что радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен касательной плоскости.
25. Докажите, что если радиус сферы перпендикулярен плоскости, проходящей через его конец лежащий на сфере, то эта плоскость является касательной к сфере.
Задания к зачету
КАРТОЧКА 1
1. Сделайте рисунок цилиндра. Что называется образующими, основанием, осью, высотой цилиндра?
2. Объясните, как получить конус вращением прямоугольного треугольника.
3. Докажите, что площадь полной поверхности цилиндра равна площади боковой поверхности другого цилиндра того же радиуса, высота которого равна сумме радиуса и высоты данного цилиндра.
КАРТОЧКА 2
1. Какой фигурой является развертка боковой поверхности цилиндра? Ответ поясните рисунком.
2. Объясните, как получить усеченный конус вращением прямоугольной трапеции.
3. Выведите формулу площади боковой поверхности цилиндра.
КАРТОЧКА 3
1. Что представляет собой сечение цилиндра, если секущая плоскость проходит через ось цилиндра? Как называется такое сечение? Ответ поясните рисунком.
2. Перечислите случаи взаимного расположения сферы и плоскости. Ответ поясните рисунком.
3. Выведите формулу площади боковой поверхности конуса.
КАРТОЧКА 4
1. Имеет ли цилиндр: а) центр симметрии; б) ось симметрии; в) плоскость симметрии? Ответ обоснуйте.
2. Что представляет собой сечение конуса плоскостью, перпендикулярной оси конуса? Ответ поясните рисунком.
3. а) Исследуйте взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.
б) Докажите, что всякое сечение шара плоскостью представляет собой круг. Центр этого круга есть основание перпендикуляра, опущенного центра шара на секущую плоскость.
КАРТОЧКА 5
1. Сделайте рисунок конуса. Что называется образующими, вершиной, высотой, основанием конуса?
2. Какой фигурой является сечение цилиндра плоскостью: а) параллельной основанию; б) параллельной оси? Ответ поясните рисунком.
З. Выведите формулу площади боковой поверхности усеченного конуса.
КАРТОЧКА 6
1. Имеет ли шар: а) оси симметрии; б) плоскость симметрии? Ответ поясните.
Ответ: а) бесконечное множество; б) бесконечное множество.
2. Какой фигурой является: а) осевое сечение конуса; б) сечение конуса плоскостью, параллельной основанию? Ответ поясните рисунком.
Ответ: а) равнобедренным или равносторонним треугольником: б) кругом или точкой.
3. Выведите формулу площади поверхности сферы.
КАРТОЧКА 7
1. Что представляет собой сечение конуса плоскостью, перпендикулярной оси конуса? Ответ поясните рисунком.
2. Может ли касательная плоскость иметь со сферой несколько общих точек? Ответ обоснуйте.
3. а) Докажите, что радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен касательной плоскости
б) Докажите, что через любую точку шаровой поверхности проходит бесконечное множество касательных, причем все они лежат в касательной плоскости шара.
КАРТОЧКА 8
1. Какая фигура получается при вращении равнобедренного треугольника вокруг его оси симметрии? Ответ поясните рисунком.
2. Имеет ли конус: а) ось симметрии; б) центр симметрии; в) плоскость симметрии?
3. а) Докажите, что если радиус сферы перпендикулярен плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
б) Докажите, что касательная плоскость имеет с шаром только одну общую точку - точку касания.
КАРТОЧКА 9
1. Сделайте рисунок сферы. Что называется центром, радиусом, диаметром сферы?
2. В каком случае осевым сечением цилиндра является квадрат, а осевым сечением конуса - равносторонний треугольник? Ответ поясните рисунком.
3. Докажите, что полная поверхность равностороннего конуса равновелика поверхности шара имеющего диаметром высоту конуса.
Объемы тел
Подготовка к зачету
Вопросы
1. Сформулируйте основные свойства объемов тел.
2. Как найти объем прямоугольного параллелепипеда, зная длины трех ребер, выходящих из одной вершины?
3. Докажите, что объем прямой призмы равен произведению площади основания на высоту.
4. Докажите, что объем наклонной призмы равен произведению площади основания на высоту.
5. Докажите, что объем любой призмы равен произведению площади ее основания на высоту.
6. Докажите, что объем наклонного параллелепипеда равен произведению площади основания на высоту.
7. Докажите, что объем треугольной пирамиды равен одной трети произведения площади основания на высоту.
8. Докажите, что объем пирамиды равен одной трети произведения площади основания на высоту.
9. Докажите, что объем цилиндра равен произведению площади основания на высоту.
10. Докажите, что объем конуса равен одной трети произведения площади основания на высоту.
11. Выведите формулу объема усеченной пирамиды.
12. Выведите формулу объема шара.
13. Выведите формулу объема шарового слоя.
Задания к зачету
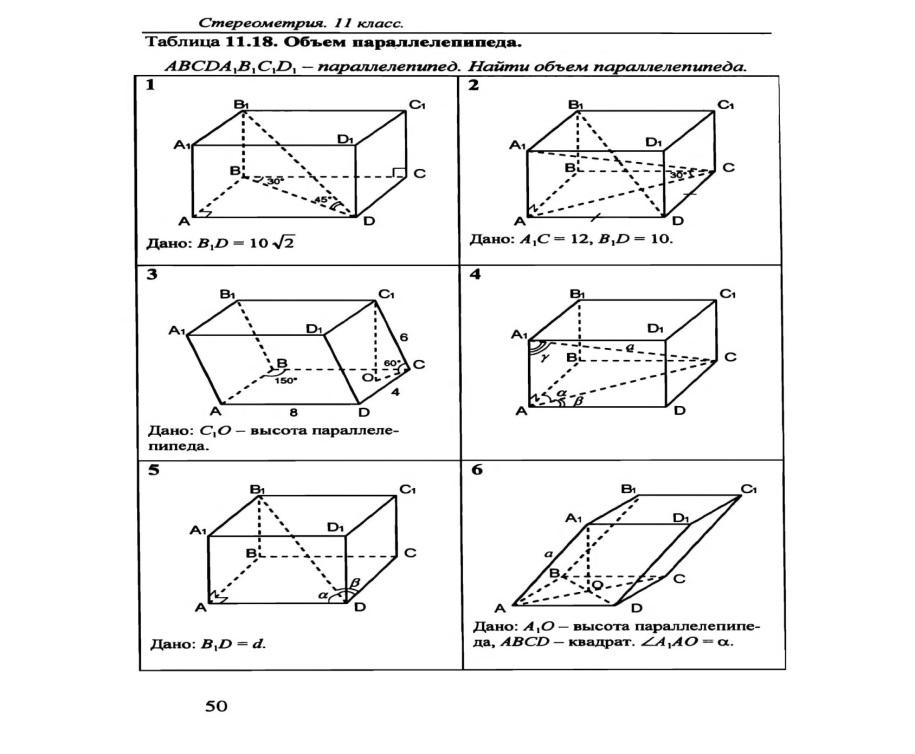
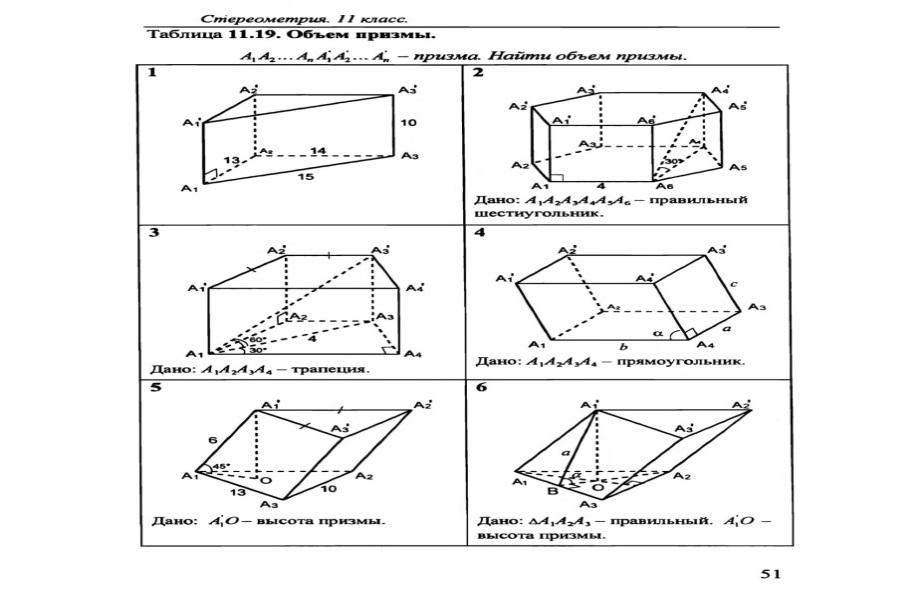
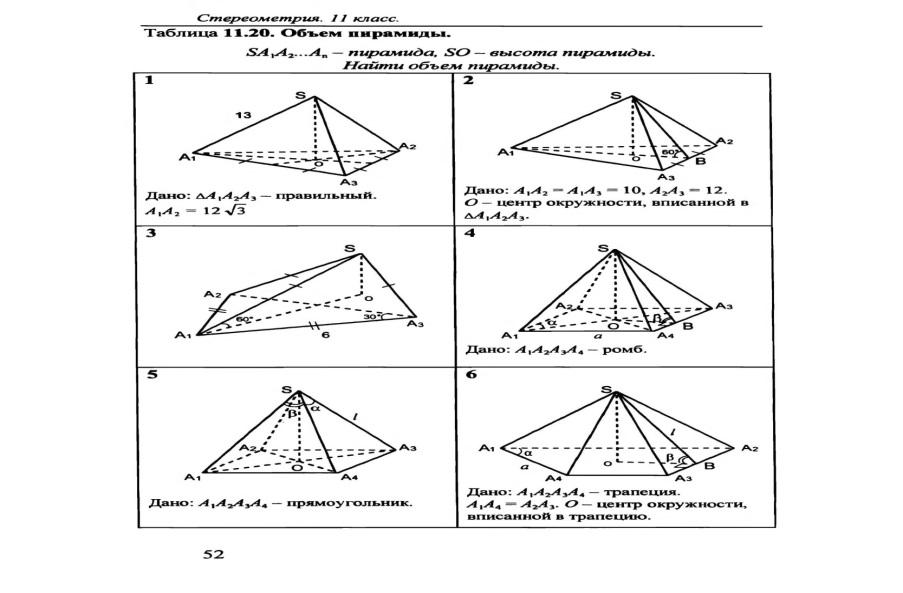
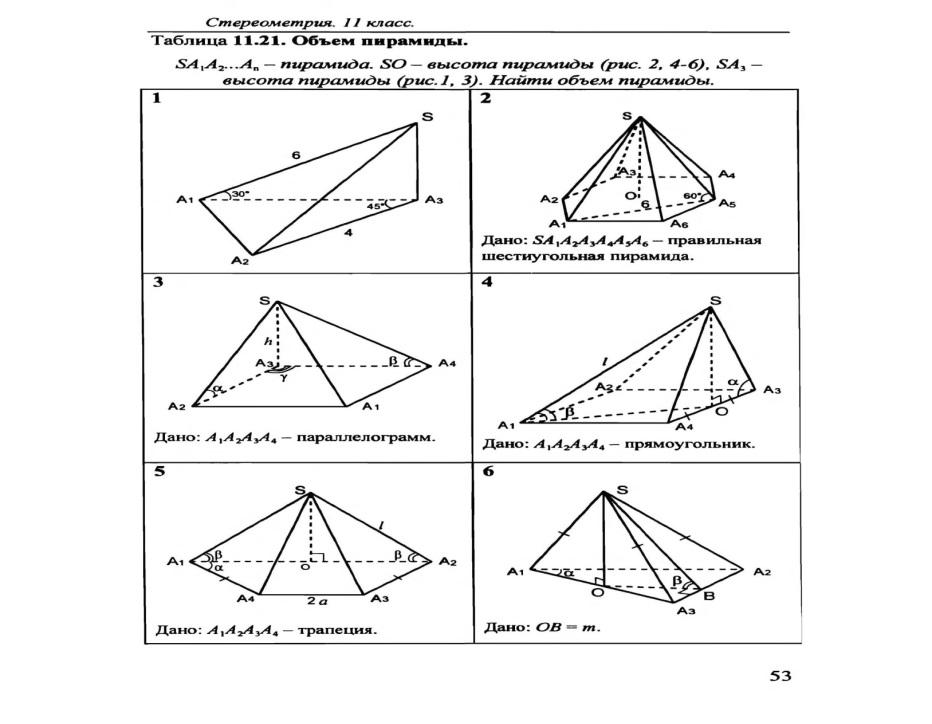
КАРТОЧКА 1
1. Запишите формулы объемов конуса и его пятой части.
2. Диагональ основания правильной четырехугольной пирамиды равна  , высота пирамиды равна
, высота пирамиды равна 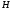 . Чему равен объем пирамиды?
. Чему равен объем пирамиды?
3. а) Зная формулу объема прямоугольного параллелепипеда, докажите, что объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
б) Зная формулу объема прямоугольного параллелепипеда, докажите, что объем любого параллелепипеда равен произведению площади основания на высоту.
КАРТОЧКА 2
1. Запишите формулу объемов пирамиды и ее третьей части.
2. Чему равен объем шара, если площадь его сферической поверхности равна ?
3. а) Зная формулу объема прямой призмы, основанием которой является прямоугольный треугольник, выведите формулу объема прямой треугольной призмы.
б) Зная формулу объема любого параллелепипеда, докажите, что объем треугольной призмы равен произведению площади ее основания на высоту.
КАРТОЧКА 3
1. Запишите формулы объемов цилиндра и его двадцатой части.
2. Осевое сечение конуса - равносторонний треугольник. Чему равна образующая конуса, если радиус основания равен ?
3. а) Зная формулу объема прямой треугольной призмы, докажите, что объем прямой призмы равен произведению площади основании на высоту.
б) Зная формулу объема треугольной призмы, докажите, что объем любой призмы равен произведению площади ее основания на высоту.
КАРТОЧКА 4
1. Запишите формулы объемов шара и его двенадцатой части.
2. Во сколько раз нужно увеличить диаметр шара, чтобы его объем увеличился в два раза?
3. а) Докажите, что объем треугольной наклонной призмы равен произведению площади основания на высоту.
б) Докажите, что объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту.
КАРТОЧКА 5
1. Запишите формулы объемов куба и его десятой части.
2. Осевое сечение конуса - прямоугольный треугольник. Чему равен диаметр основания конуса, если его образующая равна  см?
см?
3. а) Зная формулу объема наклонной треугольной призмы, докажите, что объем произвольной наклонной призмы равен произведению площади основания на высоту.
б) Зная формулу объема любой треугольной пирамиды, докажите, что объем любой пирамиды равен одной трети произведения площади ее основания на высоту.
КАРТОЧКА 6
1 Куб пересечен диагональной плоскостью, Чему равен объем каждой части куба?
2. Как вычислить объем цилиндра, зная диаметр его основания и высоту
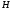 ?
?
3. Выведите формулу объема конуса.
КАРТОЧКА 7
1. Прямоугольный параллелепипед пересечен диагональной плоскостью. Чему равен объем каждой его части?
2. Радиус шара равен радиусу основания равностороннего конуса. Какое из тел имеет больший объем?
Ответ: объем шара больше, так как при данном условии объем конуса можно рассматривать как часть объема шара, описанного около конуса.
3. а) Зная формулу объема треугольной пирамиды, докажите, что объем произвольной пирамиды равен одной трети произведения площади основания на высоту.
б) Выведите формулу объема шарового слоя.
КАРТОЧКА 8
1. Чему равен объем правильной четырехугольной призмы, если сторона основания равна  м, высота призмы
м, высота призмы 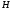 м?
м?
2. Угол между образующей конуса и радиусом основания равен , образующая конуса равна
. Чему равен объем конуса?
3. Выведите формулу объема цилиндра.
КАРТОЧКА 9
1. Угол между образующей конуса и плоскостью основания равен . Радиус основания равен
. Запишите формулу для объема конуса.
2. Радиус шара равен радиусу основания равностороннего цилиндра. Какое из тел имеет больший объем?
З. Выведите формулу объема шара.
КАРТОЧКА 10
1. Запишите формулу объема для правильной треугольной призмы, каждое ребро которой равно  .
.
2. Даны равносторонние цилиндр и конус с равными радиусами оснований. Объем, какого тела больше? Ответ обоснуйте.
Ответ: объем цилиндра больше, так как при данном условии объем конуса можно рассматривать как часть объема цилиндра, описанного около конуса.
3. Дана наклонная треугольная призма с боковым ребром, равным  . Сечение, перпендикулярное боковым ребрам, треугольник с катетами
. Сечение, перпендикулярное боковым ребрам, треугольник с катетами 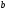 и
и . Докажите, что объем призмы вычисляется по формуле
.
Просмотр содержимого документа
«Контрольные работы 11 кл.»
Контрольная работа № 1 урок 5 ,11 класс
1. Векторы а и АВ равны. Найдите координаты точки А , если а {-1;2;4}, В(2;0;5).
2. Даны векторы а = 4 i – 3 j ; b {-3;1;2} . Найдите координаты вектора с если с = 2 а – 3 b.
3. Найдите значение m и n , при которых векторы а и b коллинеарны , если а {1;-2;m}, b{n;6;3}
Контрольная работа №1 урок 7
По теме : Простейшие задачи в координатах
1 вариант
1. Найдите координаты вектора АВ, если А(5;-1;3) , В(2;-2;4)
2. Даны векторы b {3;1;-2} и c{1;4;-3}. Найдите /2b-c/
3. Изобразите систему координат Охуz и построить точку А(1;-2;-4). Найти расстояние от этой точки до координатных плоскостей.
4. Вершины ∆АВС имеют координаты А (-2;0;1), B(-1;2;3) , C(8;-4;9). Найдите координаты вектора ВМ, если ВМ-медиана ∆АВС
5. Даны точки А(-1;5;3), В(7;-1;3), С(3;-2;6). Доказать, что ∆АВС- прямоугольный.
Контрольная работа №1 урок 7
По теме : Простейшие задачи в координатах
2 вариант
1. Найдите координаты вектора СД, если С(6;3;-2) , Д(2;4;-5)
2. Даны векторы а {5;-1;2} и b{3;2;-4}. Найдите /а-2b/
3. Изобразите систему координат Охуz и построить точку В(-2;-3;4). Найти расстояние от этой точки до координатных плоскостей.
4. Вершины ∆АВС имеют координаты А (-1;2;3), B(1;0;4) , C(3;-2;1). Найдите координаты вектора АМ, если АМ-медиана ∆АВС
5. Даны точки А(-1;5;3), В(-1;3;9), С(3;-2;6). Доказать, что ∆АВС- прямоугольный.
Контрольная работа №2
Вариант 1.
1. Даны векторы а и b, причем а = 6i – 8k, / b / = 1, ( a ^b ) = 60⁰. Найти:
а) a · b;
б) значение m, при котором векторы a и c {4; 1; m} перпендикуляры.
2. Найдите угол между прямыми АВ и СD, если А (3, -1, 3), В (3, -2, 2), С (2,2,3) и D (1,2,2).
3. Вычислите скалярное произведение векторов m и n, если m = a + 2b – c, n = 2a – b, /a/ = 2, / b / = 3,
(a ^ b) = 60⁰, c ┴ a, c ┴ b.
4. Дан правильный тетраэдр DABC с ребром а. При симметрии относительно плоскости АВС точка D перешла в точку D1. Найдите DD1.
Контрольная работа №2
Вариант 2.
1. Даны векторы a и b, причем а = 4j – 3k, / b / = √2, (a ^ b) = 45⁰. Найдите:
а) а · b;
б) значение m, при котором векторы а и с {2, m, 8} перпендикуляры.
2. Найдите угол между прямыми АВ и СD, если А (1,1,2), В (0,1,1), С (2, -2, 2) и D (2, -3, 1).
3. Вычислите скалярное произведение векторов m и n, если m = 2а – b + с, n = a – 2b, / a / = 3, / b / = 2,
( a ^ b ) = 60⁰, c ┴ a, c ┴ b
4. Дан правильный тетраэдр DАВС с ребром а. При симметрии относительно точки D плоскость АВС перешла в плоскость А1 В1 С1 . Найдите расстояние между этими плоскостями.
Контрольная работа № 3
«Цилиндр, конус и шар»
1 вариант
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 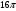 см2. Найдите площадь полной поверхности цилиндра.
см2. Найдите площадь полной поверхности цилиндра.
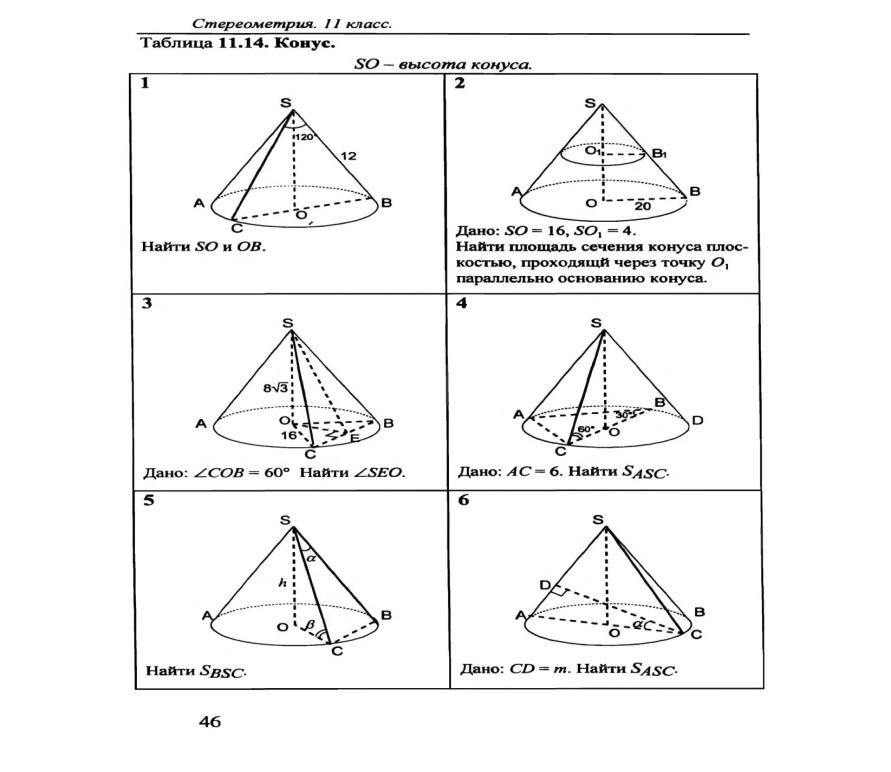
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 1200. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 300; б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 450 к нему. Найдите длину линии пересечения сферы этой плоскостью
2 вариант
1. Осевое сечение цилиндра – квадрат, диагональ которого равна 4 см. Найдите площадь полной поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 300. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 600; б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 300 к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа №4 11кл. стр207
Вариант 1
1. Апофема правильной треугольной пирамиды равна 4см, а двухгранный угол при основании равен 600. Найдите объем пирамиды.
2. В цилиндр вписана призма . Основание призмы служит прямоугольный треугольник , катет которого равен 2а , а прилежащий угол равен 300. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 450. Найдите объем цилиндра.
Контрольная работа №4 11кл. стр207
Вариант 2.
1. Боковое ребро правильной треугольной пирамиды равно 6см и составляет с плоскостью основания угол в 600. Найдите объем пирамиды.
2. В конус вписана пирамида. Основанием служит прямоугольный треугольник , катет которого равен 2а , а прилежащий угол равен 300. Боковая грань пирамиды , проходящая через данный катет, составляет с плоскостью основания угол в 450. Найдите объем конуса.
Цилиндр, конус и шар
Вариант 1
1) Осевое сечение цилиндра - квадрат. Площадь основания цилиндра равна 16π см². Найдите площадь полной поверхности цилиндра.
2) Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.
б) Найти площадь боковой поверхности конуса.
3) Диаметр шара равен 2р. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.
4) Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 5 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.
5) Плоскость, проходящая через центр нижнего основания цилиндра под углом α к основанию, пересекает верхнее основание по хорде, равной b и стягивающей дугу β. Найдите высоту цилиндра.
Цилиндр, конус и шар
Вариант 2
1) Осевое сечение цилиндра – квадрат, диагональ которого равна 4см. Найдите площадь полной поверхности цилиндра.
2) Радиус основания конуса равен 6см, а образующая наклонена к плоскости основания под углом 30º.
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60º.
б) Найти площадь боковой поверхности конуса.
3) Диаметр шара равен 4р. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите площадь сечения шара этой плоскостью.
4) Прямоугольный треугольник с катетами 30 и 40 см вращается вокруг гипотенузы. Найдите площадь поверхности тела, полученного при вращении.
5) Высота цилиндра на 2 см меньше его радиуса. Площадь боковой поверхности цилиндра равна 160π см2. Найдите площадь осевого сечения цилиндра. Найдите площадь сечения цилиндра, проведённого параллельно его оси на расстоянии 6 см от неё.
Домашняя контрольная работа
урок 45 11кл
1. Найти объем тела , полученного вращением равнобедренного треугольника около оси L, проходящей через вершину основания параллельно боковой стороне . Длина боковой стороны равна а , угол при вершине равен ß (ß
2. Образующая конуса равна √6см и составляет с площадью основания угол 450. Найдите V конуса.
3. Стог сена имеет форму цилиндра с коническим верхом. Радиус основания 2,5м, высота 4м, причем цилиндрическая часть стога имеет высоту 2,2 м. Плотность сена 0,03г/см3. Определить массу стога сена.
4. По данным радиусам R и r определите отношение объемов усеченного и полного конуса.
5. Два конуса имеют концентрические основания и один и тот же угол , равный ß , между высотой и образующей. Радиус основания внешнего конуса равен R . Боковая поверхность внутреннего конуса в два раза меньше полной поверхности внешнего конуса. Найдите объем внутреннего конуса.
Контрольная работа урок 53
По темам «Объем шара» и «Площадь сферы»
Вариант 1
Уровень 1
1.Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96П³ см³. Площадь его осевого сечения 48см². Найдите площадь сферы, описанной около цилиндра.
Уровень 2
1.Медный куб, ребро которого 10см, переправлен в шар. Найдите радиус шара.
2. Радиус шара равен R. Определите объем шарового сектора, если дуга в осевом сечении сектора равен 90°.
3. Внешний диаметр полого шара 18см, толщина стенок 3см. Найти объем стенок.
Контрольная работа урок 53
По темам «Объем шара» и «Площадь сферы»
Вариант 2
Уровень 1
1.В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов шара и цилиндра.
Уровень 2
1.Свинцовый шар, диаметр которого 20см, переплавлен в шарики с диаметром в 10 раз меньше. Сколько таких получилось?
2. Радиус шара равен R. Определите объем шарового сектора, если дуга в его осевом сечении равна 60°.
3. Поверхность шара равна 225П м². Определите его объем.
Просмотр содержимого документа
«Математические диктанты 11 кл.»
Диктант Повторение.
1. Дайте определение угла между прямыми. (Дайте определение угла между прямой и плоскостью.)
2. Выполните чертеж прямой, параллельной плоскости (двум параллельным плоскостям).
3. Дайте определение прямой, перпендикулярной к плоскости. (Сформулируйте теорему о трех перпендикулярах).
4. Постройте угол между прямой и плоскостью. (Постройте перпендикулярные плоскости).
5. Дайте определение параллельных плоскостей. (Дайте определение прямой, параллельной плоскости.)
Геометрия 11 кл. урок 5-6
1. Что называется вектором ?
2. Что называется длиной вектора?
3. Какие вектора называются коллинеарными?
4.Какие вектора называются компланарными?
Математический диктант
1. На каком расстоянии от плоскости хОу находится точка А (2;-3;-5)
2. На каком расстоянии от начала координат находится точка А(-3;4;0)
3. Найдите координаты середины отрезка, если его концы имеют координаты А(5;3;2) , В(3;-1;-4)
4. Найти длину вектора ВА , если А(-3;2;-4) , В(1;-4;2)
5. Записать координаты вектора а , если а = 4 i – 3 k
Урок 23 Геом. 11кл
Математический диктант
1 вариант
1. Найдите координаты центра и радиуса сферы, заданной уравнением (х-2) + (у+3) + z = 25.
2. Напишите уравнение сферы радиуса R=7 с центром в точке А(2;0;-1).
3. Лежит ли точка А(-2;1;4) на сфере, заданной уравнением (х+2) + (у-1) + (z -3) = 1.
4. Точки А и В принадлежит сфере. Принадлежит ли сфере любая точка отрезка АВ?
5. Могут ли все вершины прямоугольного треугольника с катетами 4см и 2 2 см лежать на сфере радиуса 5 см.
6. Записать формулу площади круга.
7. Найти координаты центра и радиуса сферы х - 6х + у + z =0
Урок 23 Геом. 11кл
Математический диктант
2 вариант
1.Найдите координаты центра и радиус сферы, заданной уравнением (х+3) + у + (z-1) =16
2. Напишите уравнение сферы радиуса R=4 с центром в точке А(-2;1;0)
3. Лежит ли точка А(5;-1;4) на сфере, заданной уравнением (х-3) +(у-1) +(z-4) =4.
4. Точки А и В принадлежат шару. Принадлежит этому шару любая точка отрезка АВ?
5. Могут ли все вершины прямоугольного треугольника с катетами 4см и 2 2 см лежать на сфере
радиуса 6 см .
6. Записать формулу длины окружности.
7. Найти координаты центра и радиус сферы х + у + 6у + z = 0
Диктант Двугранные углы. Многогранные углы.
Многогранники.
1. Что такое двугранный угол (трехгранный угол)?
2. Какими фигурами являются грани трехгранных углов (грани двугранных углов)?
3. Постройте трехгранный угол. Укажите ребра, грани. Запишите обозначение трехгранного угла. (Постройте линейный угол двугранного угла. Запишите обозначение двугранного угла и линейного угла двугранного угла.)
4. Какими фигурами являются ребра трехгранных углов (двугранных углов)?
5. Что такое многогранник ? (Какой многогранник называется выпуклым?)
6. Начертите куб. Сколько у куба ребер? Обозначьте ребра, входящие из одной вершины. (Начертите куб. Сколько у куба вершин? Обозначьте вершины, принадлежащие одной грани.)
Математический диктант разные задачи на многогранники
Вариант 1
1. Какая фигура получается в сечении конуса плоскостью, проходящей через ось конуса?
2. Какая фигура получается в сечении цилиндра плоскостью, проходящей перпендикулярно оси цилиндра?
3. Что представляет собой сечение конуса плоскостью, проходящей через вершину конуса?
4. Чему равна площадь осевого сечения конуса, если его высота в 2 раза больше радиуса основания и равна 5см?
5. Осевое сечение конуса прямоугольный треугольник с катетом а. Чему равна высота конуса?
Вариант 2
1. Какая фигура получается в сечении конуса плоскостью, проходящей перпендикулярно оси конуса?
2. Какая фигура получается в сечении цилиндра плоскостью, проходящей через ось цилиндра?
3. Что представляет собой сечение конуса плоскостью, параллельной двум образующим конуса?
4. Чему равна площадь осевого сечения конуса, если осевым сечением конуса является прямоугольный треугольник, а радиус основания конуса 3см?
5. Осевое сечение конуса равносторонний треугольник со стороной а. Чему равна высота конуса?
Диктант Призма.
1.Что называется основанием призмы (ребром призмы)?
2. Какая призма называется прямой? Ответ поясните рисунком. (Какая призма называется наклонной? Ответ поясните рисунком.)
3. Сколько вершин, ребре имеет шестиугольная призма? (Призма имеет 20 граней. Какой многоугольник лежит в ее основании? Сколько вершин и ребер имеет эта призма?)
4. Что является боковой гранью пятиугольной призмы? (Какими многоугольниками являются боковые грани правильной призмы?)
5.Сколько диагоналей у треугольной призмы (четырехугольной призмы?)
6. Сравните длину бокового ребра прямой призмы L с высотой H. (Сравните длину бокового ребра наклонной призмы L с высотой H.)
7. Сколько диагональных сечений у четырехугольной призмы? (Какими многоугольниками являются диагональные сечения прямой призмы?)
8. Что лежит в оснований четырехугольной призмы? (Что является основанием правильной треугольной призмы?)
9. Каким свойством обладают основания призмы? (Каким свойством обладают основания призмы?)
10. Запишите формулу площади боковой поверхности прямой призмы. (Можно ли использовать формулу площади боковой поверхности призмы для нахождения расхода плиток, требуемых для облицовки стен операционной комнаты?).
Теоретический диктант 11кл урок 52
Вариант 1
Вписать в текст недостающие по смыслу слова.
1. Всякое сечение шара плоскостью есть круг. Центр этого круга есть ……………….. перпендикуляра , опущенного из центра шара на секущую плоскость.
2. Центр шара является его ……………………... симметрии.
3. Осевое сечение шара есть …………………
4. Линии пересечения двух сфер есть…………….
5. Плоскости, равноудаленные от центра, пересекают шар по ………….….кругам.
6. Около любой правильной пирамиды можно описать сферу , причем ее центр лежит на ……..………….… пирамиды.
.
Теоретический диктант 11кл урок 52
Вариант 2
Вписать в текст недостающие по смыслу слова.
1. Любая диаметральная плоскость шара является его …………… симметрии.
2. Осевое сечение сферы есть……………..
3. Центр шара , описанного около правильной пирамиды , лежит на ………………..…. пирамиды.
4. Радиус сферы , проведенный в точку касания сферы и плоскости ……………….…..к касательной плоскости.
5. Касательная плоскость имеет с шаром только одну общую точку – точку ……….
6. В любую правильную пирамиду можно вписать сферу, причем ее центр лежит на …………………... пирамиды.
Математический диктант 11кл урок 56
1 вариант
1. В каком случае три точки в пространстве не определяют положение плоскости , проходящей через эти точки.
2. Могут ли две различные плоскости иметь только одну общую точку.
3. Точка М не лежит на прямой а . Через точку М проводится прямые , пересекающие прямую а . Лежат ли эти прямые в одной плоскости.
4. Прямые а и b скрещиваются с прямой с . Могут ли прямые а и b пересекаться.
5. Прямая а параллельна плоскости φ. Существуют ли на плоскости φ прямые не параллельные а . Если да , то каково их взаимное положение.
Математический диктант 11кл урок 56
2 вариант
1. Что можно сказать о взаимном положении двух плоскостей , имеющих три общие точки, не лежащие на одной прямой.
2. Могут ли две различные плоскости иметь только две общие точки.
3. Прямые а и b пересекаются в точке М . Прямая с , не проходящей через точку М , пересекает прямые а и b . Лежат ли все эти прямые в одной плоскости.
4. Прямые а и b скрещиваются с прямой с . Могут ли прямые а и b быть параллельными
5. Две прямые параллельны одной и той же плоскости. Можно ли утверждать, что эти прямые параллельны между собой . Если нет , то каково их взаимное положение.
Просмотр содержимого документа
«Самостоятельные работы 11 кл.»
Самостоятельная работа
«Координаты точки и координаты вектора»
1 вариант
1. Даны векторы 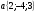 и
и  . Найдите координаты вектора
. Найдите координаты вектора 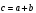 .
.
2. Даны векторы 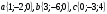 . Найдите координаты вектора
. Найдите координаты вектора 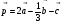 .
.
3. Найдите значения  и
и  , при которых векторы
, при которых векторы 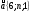 и
и 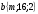 коллинеарны.
коллинеарны.
2 вариант
1. Даны векторы 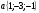 и
и 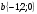 . Найдите координаты вектора
. Найдите координаты вектора 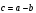 .
.
2. Даны векторы 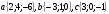 . Найдите координаты вектора
. Найдите координаты вектора 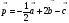 .
.
3. Найдите значения 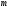 и
и  , при которых векторы
, при которых векторы 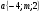 и
и 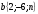 коллинеарны.
коллинеарны.
(урок 1-4)
Прямоугольная система в пространстве.
Координаты вектора.
Связь между координатами векторов и координат точек.
1. Даны точки А(-1;7 и В(7;1) Найти середину отрезка А
2. Запишите координаты вектора m= -3i+2j+5k
3.Сколькими координатами может быть задана точка на прямой , на плоскости , в пространстве.
4.Е(-2;3;5) , F(1;2;8) Найдите координаты вектора ЕF
5.Как называются координаты точки в пространстве
6. Дать определение вектора
7. Дать определение компланарных векторов
8. Как располагаются точки относительно координат , если а) одна координата равна нулю
б) две ее координаты равны нулю.
9. Почему все точки , лежащие на прямой , параллельной плоскости Оху , имеют одну и туже аппликату.
10. Какие вектора называются равными
11. Постройте точки А(2;4;5) B(0;0;3) S(2;3;3) ,C(2;0;0), D(0;4;0) E(3;2;-4) R(4;-1;3)
12. Даны векторы а{3;5;-7} ,b {4;-1;3} c{0;1;8} d{3;0;0} p{-5;-3;1} s{3;-2;5}
а) разложить векторы по координатным векторам
б) найти вектор 2 а , 3с , -4 s , а+b , d+p , s +a , b – p , s – c, c + d – s
в) построить вектор q {2;4;5}
13. Укажите координаты векторов i и k и j
14. На какой координатной оси или в какой координатной плоскости лежат точки , если
А(2;3;0) В(0;0;4) C(3;0;1) M(0;8;0) N(0;2;6) K(-7;0;7)
15.Записать разложение векторов а {3;-2;8} b{ 7;0;-1/3} c{-0,2;6;11}
16. Записать координаты n и m , если n=3i+ 2 j – k , m = j +0,8 k , n = 5 I – j
17. В какой координатной плоскости лежит вектор а если a = -2 i + 3 k , a =j +5 k
18. На какой координатной оси лежит вектор b если а) b {3;0;0} б) b {0;0;-7} в) b ={0;5;0}
(урок 1-4)
Прямоугольная система в пространстве.
Координаты вектора.
Связь между координатами векторов и координат точек.
1.Даны векторы а {2:-4;3} и b {-3;1/2;1} . Найти координаты вектора с = а + b.
2. Даны векторы а {1;-2;0} , b {3;-6;0} и c {0;-3;4} . Найдите координаты вектора
p = 2 a – 1/3 b – c .
3. Найдите значение m и n , при которых вектора а и b коллинеарны , если а{6;n;1} и b {m;16;2}
Простейшие задачи
1. Найдите координаты вектора СД , если С(6;3;-2) , Д(2;4;-5).
2. Даны векторы а {5;-1;2} и b{3;2;-4}. Найти / a - 2 b/
3. Изобразить систему координат Охуz и построить точку В (-2;-3;4). Найти расстояние от точки до
координатных плоскостей.
4. Векторы а и АВ равны . Найдите координаты точки А, если а {-1;2;4} точка В (2;0;5)
Дано: А(х;у;z), а {-1;2;4} В (2;0;5) а = АВ
Найти : х;у;z.
Решение: АВ {2-х; -у; 5-z} , а {-1;2;4} = АВ {2-х; -у; 5-z} , -1=2-х , х=3 ; -у=2, у= -2; 4=5-z, z=1
Ответ : х=3, у=-2, z=1.
C/р. Даны векторы а и АВ . Найдите координаты точки В , если а {2;-3;1} точка А(1;4;0)
5. Даны векторы а = 4 i-3 j ; b {-3;1;2}. Найдите координаты вектора с , если с = 2 а – 3 b.
Дано: а = 4 i – 3j , b {-3;1;2}, с = 2 а – 3 b.
Найти: c { х;у;z}
Решение: а {4;-3;0}, b {-3;1;2}. с = {8;-6;0} - {-9;3;6} = {17;-9;-6}
Ответ: {17;-9;-6}
С/р. Даны векторы а =- i + 2k . b{2;6;-4}. Найдите координаты вектора с , если с = ½ b – 2 a.
6. Найдите значение m и n, при которых векторы а и b коллинеарны , если а {1;-2;m}, b {n;6;3}
Дано: а {1;-2;m}, b {n;6;3} , а и b коллинеарны.
Найти: m и n.
Решение: а = k b, -2= k. 6 k=-1/3 ; 1=-1/3. n , n= -3 ; m = -1/3. 3 , m=-1.
Ответ: m=-1 , n=-3
C/р. Найдите значение m и n , при которых векторы а и b коллинеарны , если а{2;m;1}, b{4;-2;n}
С/р. Даны точки А(-1;5;3), В(-1;3;9), С(3;-2;6) . Доказать что треугольник прямоугольный
Вершины
если АМ – медиана
Решение: Так как АМ медиана , то она делит противоположную сторону треугольника пополам .
Найдем середину отрезка ВС точку М (2; -1; 2,5) . Зная координаты точки А и М найдем
координаты вектора АВ {3;-3;-0,5}.
Ответ: {3;-3;-0,5}
Самостоятельная работа
«Метод координат в пространстве»
Вариант 1
Даны точки А(5; 0; 2), В(4; -3; 2),
С(0; 0; 1), D(2; -4; -4). Найдите:

 а) координаты векторов АВ и СD;
а) координаты векторов АВ и СD;


 б) координаты векторов а = АВ + СD,
б) координаты векторов а = АВ + СD,




 b = AB – CD, с = -⅓АВ;
b = AB – CD, с = -⅓АВ;

 в) длины векторов а и b;
в) длины векторов а и b;
г) скалярное произведение векторов



 АВ и СD, а и b.
АВ и СD, а и b.
2. Вершины треугольника КМN имеют координаты K(-2; 3; -2), M(8; 1;2), N(2; -3; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
Самостоятельная работа
«Метод координат в пространстве»
Вариант 2
Даны точки А(5; -5; 0), В(-2; 1; -3),
С(0; 3; 1), D(1; 3; -4). Найдите:

 а) координаты векторов АВ и СD;
а) координаты векторов АВ и СD;


 б) координаты векторов а = АВ + СD,
б) координаты векторов а = АВ + СD,




 b = AB – CD, с = ⅓АВ;
b = AB – CD, с = ⅓АВ;

 в) длины векторов а и b;
в) длины векторов а и b;
г) скалярное произведение векторов



 АВ и СD, а и b.
АВ и СD, а и b.
2. Вершины треугольника КМN имеют координаты K(8; 3; 5), M(14; 1;0), N(12; -5; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
Самостоятельная работа
«Скалярное произведение векторов»
1 вариант
1. Даны векторы и
. Вычислите
.
2. Вычислите угол между прямыми АВ и CD, если.
2 вариант
1. Даны векторы и
. Вычислите
.
2. Вычислите угол между прямыми АВ и CD, если .
Самостоятельная работа
«Цилиндр»
1 Вариант
1. Развёртка боковой поверхности цилиндра является квадратом, диагональ которого равна 10 см. Найдите площадь боковой поверхности цилиндра.
2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 1200. Высота цилиндра равна 5 см, радиус цилиндра см. Найдите площадь сечения.
2 вариант
1. Развёртка боковой поверхности цилиндра является квадратом, диагональ которого равна 10 см. Найдите площадь боковой поверхности цилиндра.
2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 1200. Высота цилиндра равна 5 см, радиус цилиндра см. Найдите площадь сечения.
Самостоятельная работа по геометрии 11 класс «Цилиндр»
Вариант 1
Изобразите цилиндр и все его составляющие.
Что называют цилиндром?
__________________________________________________________________________________________3. Основания цилиндра –
__________________________________________________________________________________________
4.Высота цилиндра-______________________________________________________________________________________
5.Радиус цилиндра -______________________________________________________________________________________
6.Площадь бок. поверх. цилиндра - ____________________________________________________________________________
7.Площадь полной поверхности цилиндра ______________________________________________________________________________________
8. Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см.
Найдите: а) высоту цилиндра; б) площадь основания цилиндра.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.Радиус основания цилиндра равен 2м, высота 3м. Найдите площадь осевого сечения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельная работа
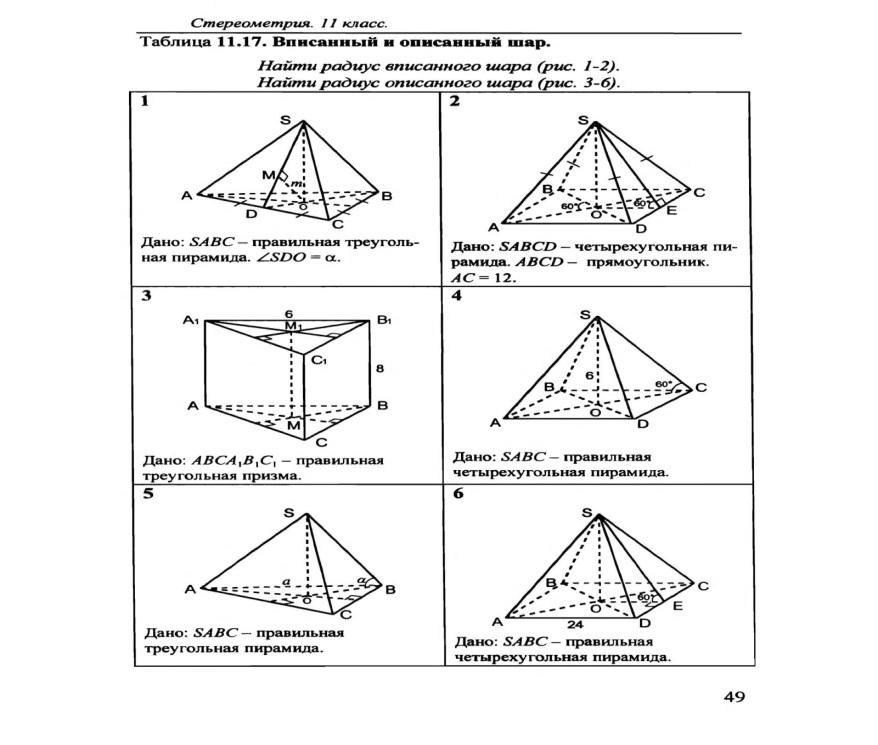
№1. В правильную четырехугольную пирамиду вписан шар, объем которого 32p/3. Найдите объем пирамиды, если её высота равна 6.
№2. В шар, объём которого 500/3, вписана правильная четырехугольная пирамида. Найдите объём пирамиды, если её боковое ребро равно 3, а высота больше радиуса шара.
№3. Площадь поверхности сферы, вписанной в конус, равна 100p. Длина окружности, по которой сфера касается поверхности конуса, равна 6p. Найдите радиус основания конуса.
№4. В конус с образующей 6 и высотой 12 вписан куб. Найдите объём куба.
№5. Площадь основания конуса равна площади поверхности вписанного в него шара. Найдите радиус шара, если образующая конуса равна 10.
Обучающая самостоятельная работа
Вариант 1.
Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d.
1) Докажите, что сечение цилиндра плоскостью g есть прямоугольник.
2) Найдите AD, если a =10 см, a = 60°.
Обучающая самостоятельная работа
Вариант 2.
Плоскость g, параллельная оси цилиндра, отсекает от окружности основания дугу AmD с градусной мерой a. Радиус цилиндра равен a, высота равна h, расстояние между осью цилиндра ОО1 и плоскостью g равно d.
1) Составьте план вычисления площади сечения по данным a, h, d.
2) Найдите AD, если a =8 см, a = 120°.
Самостоятельная работа в парах.
Вариант 1.
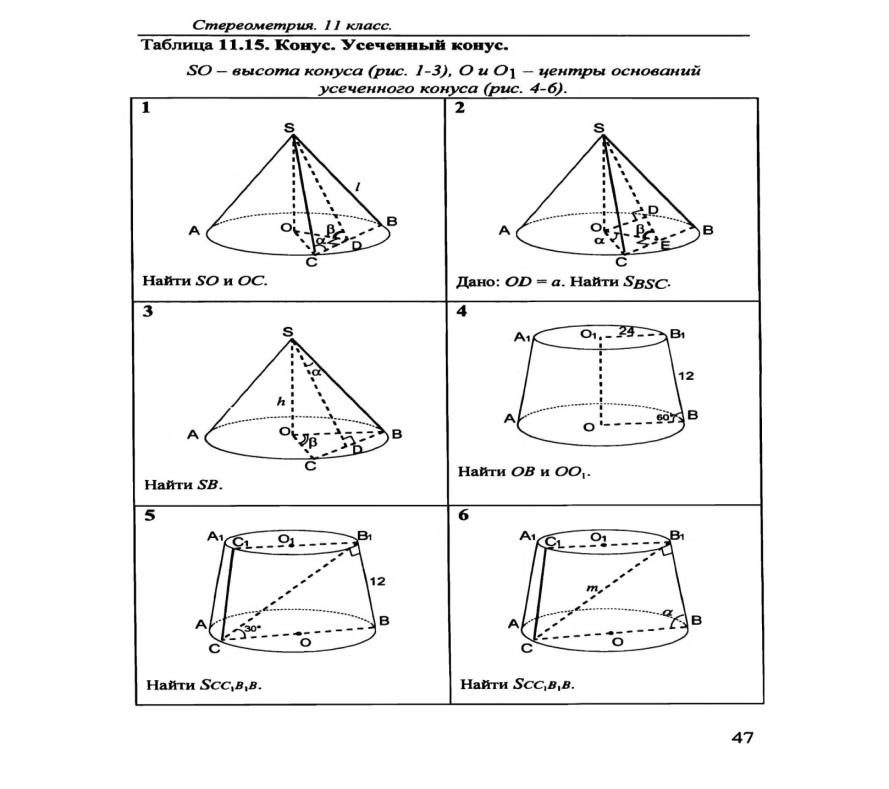
1. В осевое сечение усеченного конуса вписана окружность. Радиусы оснований конуса 16см и 25см. Найдите высоту и Sп.п. усеченного конуса.
2. В шар вписан конус, площадь осевого сечения которого равна S, угол при вершине осевого сечения равен 2 . Найдите объём шара.
Вариант 2.
1. Прямоугольный параллелепипед описан около сферы радиуса 6,5. Найдите его объем. (ЕГЭ 2010, Статград)
2. Сторона основания правильной четырехугольной пирамиды равна 10 , а угол боковой грани с плоскостью основания равен 60º. Найдите объём шара, вписанного в пирамиду.
Цилиндр. Самостоятельная работа.
1) Радиус основания цилиндра равен 4, образующая равна 6. Найдите диагональ осевого сечения цилиндра
2) Диагональ осевого сечения цилиндра равна 5, высота равна 3. Найдите радиус основания цилиндра.
3) Радиус основания цилиндра равен 3, диагональ осевого сечения равна 10. Найдите образующую цилиндра.
4) Радиус основания цилиндра равен 3, диагональ осевого сечения равна 10. Найдите образующую цилиндра.
5) Диагональ осевого сечения цилиндра равна 6 и наклонена к плоскости основания цилиндра под углом 30°. Найдите образующую цилиндра .
6) Радиус основания цилиндра равен 2. Диагональ осевого сечения цилиндра наклонена к плоскости основания цилиндра под углом 45°. Найдите образующую цилиндра .
7) Образующая цилиндра равна 10. Диагональ осевого сечения цилиндра наклонена к плоскости основания цилиндра под углом 45°. Найдите радиус основания цилиндра.
8) Диагональ осевого сечения цилиндра равна 6 и наклонена к плоскости основания цилиндра под углом 60°. Найдите радиус основания цилиндра.
9) Радиус основания цилиндра равен 3. Найдите диагональ осевого сечения цилиндра, если она наклонена к плоскости основания цилиндра под углом 60°.
Самостоятельная работа
«Объём прямоугольного параллелепипеда»
1 вариант
1. Измерения прямоугольного параллелепипеда равны 2,5 см, 5 см и 5 см. Найдите ребро куба, объём которого в два раза больше объёма данного параллелепипеда.
2. Найдите объём прямой призмы АВСА1В1С1, если угол АСВ равен 900, угол ВАС равен 300, АВ = а, СВ = ВВ1.
2 вариант
1. Измерения прямоугольного параллелепипеда равны 2 см, 6 см и 6 см. Найдите ребро куба, объём которого в три раза больше объёма данного параллелепипеда.
2. Найдите объём прямой призмы АВСА1В1С1, в которой угол АСВ равен 900, АВ = ВВ1 = а, АС = СВ.
Самостоятельная работа № 5
«Объём наклонной призмы, пирамиды и конуса»
1 вариант
Найдите объём правильной треугольной пирамиды с боковым ребром l = 10 см, если боковое ребро составляет с плоскостью основания угол, равный 300.
2 вариант
Найдите объём правильной четырёхугольной пирамиды, если её высота Н = 10 см, а двугранный угол при основании равен 600.
Тестовая самостоятельная работа 11 класс урок 52
Уровень1 Вариант 1
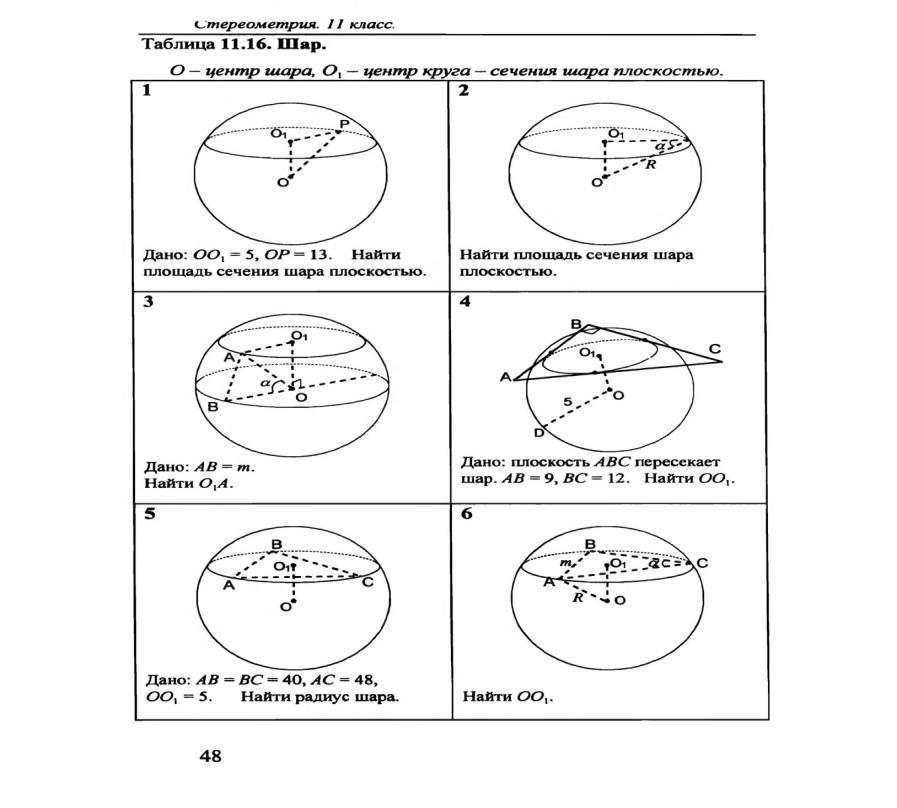
1.На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9см. Найдите объем шара и площадь его поверхности.
2. Сфера радиуса 3см имеет цент в точке О (4;-2;1). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости ОХУ. Найдите объем шара, ограниченного данной сферой.
Тестовая самостоятельная работа 11 класс урок 52
Уровень 1 Вариант 2
1.Через точку, лежащую на сфере, проведено сечение радиуса 3см под углом 60° к радиусу сферы, проведенному в данную точку. Найдите площадь сферы и объем шара.
2. Сфера радиуса 3 имеет центр в точке О (-2;5;3). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости ОХZ. Найдите площадь данной сферы.
Тестовая самостоятельная работа 11 класс урок 52
Уровень2 Вариант 1
1.На расстоянии 2√7см от центра шара проведено сечение. Хорда этого сечения, равна 4см, стягивая угол 90°. Найдите объем шара и площадь его поверхности.
2. Сфера с центром в точке О (2;1;-2) проходит через начало координат. Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно оси абцисс. Найдите объем шара, ограниченного полученной сферой.
Тестовая самостоятельная работа 11 класс урок 52
Уровень2 Вариант 2
1.На расстоянии 4см от центра шара проведено сечении. Хорда, удаленная от центра этого сечения на √5см, стягивая угол 120°. Найдите объем шара и площадь его поверхности.
2. Сфера с центром в точке О (-1;-2;2) проходит через начало координат. Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости Z=1. Найдите площадь сферы.
Самостоятельная работа №1
Вариант 1
1.Радиус шара ¾ дм. Вычислите объём шара и площадь сферы.
2.Футбольный мяч имеет диаметр 30 дм. Какой объём воздуха содержится в мяче?
Самостоятельная работа №1
Вариант 2
1.Диаметр шара ½ дм. Вычислите объём шара и площадь сферы.
2. Волейбольный мяч имеет радиус 12 дм. Какой объём воздуха содержится в мяче?
Просмотр содержимого документа
«Тесты 11 кл.»
Приложение 1
Тест Планиметрия
1 вариант
Высота равностороннего треугольника равна 15 см. Найдите радиус вписанной в треугольник окружности.
а) 5√3 см; в) 5 см; с) 6 см; д) 7 см; е) 8 см.
2. Чему равна площадь прямоугольника, если его диагональ 10 см, а одна из сторон 8 см?
а) 50 см2; в) 60 см2; с) 80 см2; д) 48 см2; е) 40 см2;
3. Окружность радиуса 4√3 см описана около правильного многоугольника со стороной 12 см. Найдите число сторон многоугольника.
а) 6; в) 5; с) 4; д) 8; е) 3.
4. Найдите сторону треугольника, лежащую против угла 120°, если две другие стороны равны 6 см и 10 см.
а) 10см; в) 14 см ; с) 15 см ; д) 13 см ; е) 12 см.
5. Найдите площадь треугольника, если ВС=7 см, АС=14 см, С=30°.
а) 18,3 см2; в) 40,1 см2; с) 12,5 см2; д) 24,5 см2; е) 31 см2;
6. Четырехугольник АВСД является ромбом, у которого сторона АВ равна 17 см, диагональ ВД равна 30 см. Найдите длину диагонали АС.
а) 8 см; в) 14 см; с) 16 см; д) 17 см; е) 20 см.
7. Дан треугольник АВС. А=120°, АС=3, АВ=2. Найдите квадрат стороны ВС.
а) 7; в) 12; с) 15; д) 10; е) 19.
8. В треугольнике АВС стороны АВ=5 см, ВС=7 см. Найдите отношение синуса угла А к синусу угла С.
а) 1; в) 5/7; с) 7/5; д) 1/2; е) 2.
9. Сторона параллелограмма равна 10 см, а диагональ, равная 12 см образует с ней угол 30°. Найдите площадь параллелограмма.
а) 90 см2; в) 45 см2; с) 120 см2; д) 75 см2; е) 60 см2;
10. В прямоугольном треугольнике один катет равен 7 , а другой – 24. Найдите радиус описанной окружности.
а) 25; в) 12,5; с) 12; д) 24; е) 7.
11. Средняя линия трапеции с основанием 4 и 6 см разбивает трапецию на две фигуры. Найдите отношение площадей этих фигур.
А) 9:8; в) 11:9; с) 4:9; д) 7:8; е) 7:6.
12. Площадь прямоугольного треугольника равна 150, один из катетов равен 15. Найдите длину высоты, опущенной из вершины прямого угла.
а) 12; в) 24; с) 20√3; д) 10√3; е) 20.
13. Высота треугольника равна 10 см, делит основание на два отрезка, равные 10 см и 4 см. Найти медиану, проведенную к меньшей из двух других сторон.
а) 14; в) 12; с) 13; д) 11; е) 12,5
14. Стороны треугольника АВС равны 13 см, 14 см, 15 см. О- точка пересечения медиан. Найдите площадь треугольника АОВ.
а) 14 см2; в) 42 см2; с) 7 см2; д) 84 см2; е) 28 см2;
Тест Планиметрия
2 вариант.
1. Точка К делит хорду АР на отрезки 12 см и 14 см. Найдите радиус окружности, если расстояние от центра окружности до точки К равно 11 см.
а) 23 см; в) 17 см; с) 11 см; д) 13 см; е) 19 см.
2. Чему равна площадь равнобедренного треугольника, если его основание 30 см, а боковая сторона 25 см?
а) 200 см2; в) 300 см2; с) 750 см2; д) 400 см2; е) 150 см2;
3. Гипотенуза прямоугольного треугольника равна 41 см, а его площадь равна 180 см2. Найдите катеты этого треугольника.
а) 40 см; 9 см; в) 41 см; 9 см; с) 9 см; 90 см;
д) 41 см; 90 см; е) 40 см; 41 см.
4. Полупериметр параллелограмма равен 32 см. Меньшая сторона его равна
15 см. Найдите большую сторону параллелограмма.
А) 17,5 см; в) 16 см; с) 18 см; д) 16,5 см; е) 17 см
5. Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза
равна 15. Найдите периметр.
а) 28; в) 34; с) 36; д) 30; е) 25.
6. Найдите площадь треугольника, если две его стороны равны 4 см и 3 см, а медиана третьей стороны равна 2,5 см.
А) 7,5 см2; в) 10 см2; с) 6 см2; д) 24 см2; е) 12 см2;
7. Диагональ квадрата 2√2 см. Найдите сторону квадрата.
а) 2,1 см; в) 4 см; с) 1,5 см; д) 3 см е) 2 см.
8. В прямоугольном треугольнике катет равен 7, а гипотенуза – 25. Найдите радиус вписанной в треугольник окружности.
а) 4; в) 10; с) 3; д) 5; е) 2.
9. В равнобедренной трапеции основания равны 10 и 24, боковая сторона 25. Найдите высоту трапеции.
а) 22; в) 28; с) 20; д) 26; е) 24.
10. Найти площадь равнобедренного треугольника, если высота, опущенная на основание, равна 10, а высота, опущенная на боковую сторону, равна 12.
а) 150; в) 50; с) 75; д) 125; е) 120.
11. Боковые стороны трапеции 13 см и 15 см. Периметр равен 48 см. Найдите среднюю линию трапеции.
а) 30 см; в) 20 см; с) 15 см; д) 10 см; е) 24 см.
12. Диагонали ромба 24 и 70. Найдите сторону ромба.
а) 37; в) 44; с) 45; д) 35; е) 42.
13. Стороны параллелограмма 4см и 6 см, а угол между ними 30°. Найдите площадь параллелограмма.
а) 11 см2; в) 9 см2; с) 18 см2; д) 12 см2; е) 7 см2;
14. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 8 м и 18 м.
а) 12 см; в) 72 см; с) 36 см; д) 24 см; е) 18 см.
Ключ к тесту по теме «Планиметрия».
1 вариант. 2 вариант
1. В 1. В
2. Д 2. В
3. Е 3. А
4. В 4. Е
5. Д 5. С
6. С 6. С
7. Е 7. Е
8. С 8. С
9. Е 9. Е
10. В 10. С
11.В 11. Д
12. А 12. А
13. С 13. Д
14. Е 14. А
Тест
«Координатный метод в пространстве»
Вариант 1
Найти длину вектора
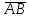 , если А (-1;-1;0); В(1;1;2).
, если А (-1;-1;0); В(1;1;2).
4
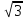
2
3
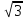
6
2
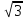
А (1;6;2), В (2;3;-1). Найти координаты вектора
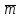 =2*
=2*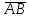
Точка М – середина отрезка AB. Найти координаты точки B, если A (14;-8;5), М (3;-2;-7).
(8,5;-5;-1)
(5,5;-3;6)
(17;-10;-2)
(-8;4;-19)
(42;16;-35)
Найти значение m, при которых длина вектора
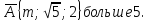
(-
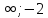 )
)
(
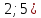
(-
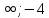 )
)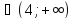
(-
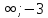 )
)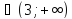
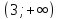
При каких значениях k и m векторы
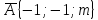 и
и 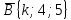 коллинеарны?
коллинеарны?
k=-
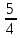 , m=4
, m=4k=4, m=
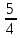
k=-4, m=-
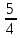
k=4, m=-
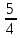
k=-4, m=
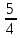
Тест
«Координатный метод в пространстве»
Вариант 2
Найти длину вектора
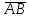 , если А (2;3;2); В(1;5;0).
, если А (2;3;2); В(1;5;0).
3
5
2
4
7
А (5;1;0), В (-2;-3;1). Найти координаты вектора
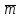 =-3*
=-3*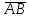
{-7;-4;1}
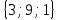
{21;12;-3}
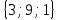
{-21;-12;3}
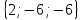
{3;-2;1}
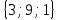

{-6;6;-3}
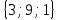
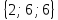
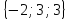
Точка М – середина отрезка AB. Найти координаты точки А, если М (-6;2;0), В (3;-2;4).
(15;-6;4)
(-15;6;-4)
(-3;0;4)
(-18;-4;0)
(-9;4;-4)
При каких значениях m длина вектора A{3;m;4} не превышает 10?
(-∞;-5√3]
(-∞;-5√3)∪(5√3;+∞)
[5√3;+∞)
(-5√3;5√3)
[-5√3;5√3]
При каких значениях k и m векторы А{4;-4;m}и B{2;k;1} коллинеарны?
k=- 4, m=-1
k=-2, m=2
k=-2, m=-2
k=2, m=- 2
k=2, m=2
Итоговый Тест №1 по теме метод координат
1) Даны векторы a {2 ;-4 ;3} b {-3; 1/2 ; 1}. Найдите координаты вектора
→ c = a+b
а) (-5; 3 ∙1/2; 4); б) (-1; -3,5;4) в) (5; -4 ∙1/2; 2) г) (-1; 3,5; -4)
→ →
2) Даны векторы a {4; -3; 5) и b {-3 ; 1; 2}. Найдите координаты вектора
→ → →
C= 2 a – 3 b
а) (7;-2;3); б) (11; -7; 8); в) (17; -9; 4); г) (-1; -3; 4).
→ → → → → →
3)Вычислите скалярное произведение векторов m и n, если m = a + 2 b- c
→ → → → →^ → → → → →
n= 2 a - b если |a|=2 , | b |=3, (a b)=60°, c ┴ a , c ┴ b.
а)-1; б)-27; в)1; г) 35.
→ →
4) Длина вектора a {x y z} равна 5. Найдите координаты вектора а , если x=2, z=-√5
а) 16; б ) 4 или -4; в) 9; г)3 или -3.
5) Найдите площадь ∆АВС, если А(1;-1;3); В(3;-1;1) и С(-1;1;-3).
а) 4√3; б) √3; в)2√3; г)√8.
Взаимопроверка теста. Коды ответов к заданиям теста на экране:1(б); 2(в);3(а); 4(б); 5(в).
ТЕСТ №2
Метод координат в пространстве. Преобразования в пространстве.
В – 1
1. Как расположены относительно системы координат точки А (1; 1; 0), В (0; 3; 0),
С (0; 0; 3), D (0; 3;4), E (2; -2; 0), F (0; -1; 0).
А: D:
B: E:
C: F:
2. Определите, верны ли утверждения:
А) начало координат имеет все три координаты, равные 0. ____________
Б) точка в пространстве определяется двумя координатами. ____________
3. Точка М является серединой отрезка АВ. Найдите координаты точки А, если В (0; 4;-7) и М (6; -5; -2).
А) (12; -14; 3) Б) (-12; 14; 3) В) (6; -5; 2)
4. Найдите расстояние от точки С (0; 6; -3) до плоскости YOZ.
А) 0 Б) 6 В) 3
5. Найдите координаты точки, симметричной точке А (2; 7; -4) относительно начала координат.
А) (-2; 7; -4) Б) (-2; -7; 4) В) (2; -7; 4)
6. Найдите координаты точки, симметричной точке А (1; 4; 2) относительно оси Ох.
А) (1; -4; 2) Б) (-1; 4; 2) В) (1; -4; -2)
7. Найдите координаты точки, симметричной точке А (2; 1; 3) относительно координатной плоскости XOY.
А) (-2; 1; 3) Б) (2; 1; -3) В) (2; -1; 3)
8. Определите, верны ли утверждения:
А) прямоугольный параллелепипед имеет единственный центр симметрии. ___________
Б) угол между параллельными прямой и плоскостью равен 90. __________
9. Используя параллельный перенос, найдите координаты точки, симметричной с точкой А (3; 4; 5) относительно Р (1; 1; 1).
ТЕСТ №2
Метод координат в пространстве. Преобразования в пространстве.
В – 2
1. Как расположены относительно системы координат точки А (2; 0; 0), В (0; -5; 0),
С (0; 0; -1), D (0; 2; 2), E (5; -5; 0), F (3; 0; -1).
А: D:
B: E:
C: F:
2. Определите, верны ли утверждения:
А) точка, лежащая на координатных плоскостях, имеет одну из координат, равную 0. ____________
Б) каждой тройке чисел соответствует три точки пространства. ____________
3. Точка М является серединой отрезка АВ. Найдите координаты точки М, если А (2; -7; 4) и В (-6; 11; 2).
А) (2; 2; 3) Б) (-2; 2; 3) В) (-2; 2; -3)
4. Найдите расстояние от точки А (2; 1; 5) до плоскости ХОY.
А) 5 Б)
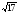 В)
В) 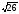
5. Найдите координаты точки, симметричной точке В (0; -3; 5) относительно начала координат.
А) (0; 3; -5) Б) (0; -3; -5) В) (0; 3; 5)
6. Найдите координаты точки, симметричной точке В (-3; 2; 4) относительно оси Оy.
А) (3; 2; -4) Б) (3; -2; 4) В) (-3; 2; -4)
7. Найдите координаты точки, симметричной точке В (-5; 2; 4) относительно координатной плоскости XOZ.
А) (-5; -2; 4) Б) (-5; 2; -4) В) (-5; -2; -4)
8. Определите, верны ли утверждения:
А) прямоугольный параллелепипед имеет одну плоскость симметрии. ___________
Б) угол между параллельными прямыми равен 0. __________
9. Используя параллельный перенос, найдите координаты точки, симметричной с точкой В (0; 2; 0) относительно Р (1; 1; 1).
Тестовая работа по теме «Цилиндр». Вариант 1.
№
задача
выбор ответа
1
Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности равна:
40
10
20
4
2
В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16 кв.дм. Найдите площадь полной поверхности цилиндра.
80
96
64
32
3
Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности равна:
16
32
4
8
4
Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, равна:
56
72
88
48
5
Если площадь боковой поверхности цилиндра равна 64 кв.м, а высота – 4 м, тогда радиус равен:
16
8
26
8
6
Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра может быть равна:
256
100
24
64
7
Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?
3
6
9
27
8
Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра может быть равна:
36
64
48
96
9
Во сколько раз уменьшится площадь боковой поверхности цилиндра, если его высоту уменьшить в 4 раза а радиус увеличить в 2 раза?
не изменится
8
4
2
10
Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту уменьшить в 3 раза а радиус увеличить в 12 раз?
4
6
не изменится
8
Тестовая работа по теме «Цилиндр». Вариант 2.
№
задача
выбор ответа
1
Диаметр основания цилиндра равен 4 см, высота – 3 см, тогда площадь боковой поверхности равна:
40
10
12
4
2
В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 9 кв.дм. Найдите площадь полной поверхности цилиндра.
40
54
60
32
3
Радиус основания цилиндра в три раза меньше образующей, равной 6, тогда площадь боковой поверхности равна:
24
32
4
8
4
Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его меньшей стороны, равна:
56
105
154
48
5
Если площадь боковой поверхности цилиндра равна 64 кв.м, а радиус – 8м, тогда образующая равна:
16
4
26
8
6
Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра может быть равна:
256
100
24
25
7
Во сколько раз увеличится площадь боковой поверхности цилиндра, если его радиус увеличить в три раза?
9
не изменится
3
27
8
Осевым сечением цилиндра является прямоугольник со сторонами 6 и 8 см, то площадь боковой поверхности цилиндра может быть равна:
9
64
36
48
9
Как изменится площадь боковой поверхности цилиндра, если его высоту увеличить в 4 раза, а диаметр уменьшить в 2 раза?
увеличится в 2раза
увеличится в 8 раз
не изменится
уменьшится в 2 раза
10
Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту уменьшить в 3 раза, а радиус увеличить в 6 раз?
2
6
не изменится
3
Урок 20 Геометрия 11 класс Конус
Тест
1 вариант
1. Какая фигура получается в сечении конуса плоскостью, проходящей через ось конуса
2. Какая фигура получается в сечении цилиндра плоскостью , проходящей перпендикулярно оси цилиндра .
3. Что представляет собой сечение конуса плоскостью , проходящей через вершину конуса.
4. Чему равна площадь осевого сечения конуса , если его высота в 2 раза больше радиуса основания и равна 5см.
5. Осевое сечение конуса представляет собой прямоугольной треугольник со стороной а . Чему равна высота конуса.
Урок 20 Геометрия 11 класс Конус
Тест
2 вариант
1. Какая фигура получается в сечении конуса плоскостью, проходящей перпендикулярно оси конуса.
2. Какая фигура получается в сечении цилиндра плоскостью , проходящей через ось цилиндра.
3. Что представляет собой сечение конуса плоскостью , параллельной двум образующим конуса.
4. Чему равна площадь осевого сечения конуса, если осевым сечением конуса является прямоугольный треугольник , а радиус основания конуса 3см.
5. Осевое сечение конуса представляет собой равносторонний треугольник с катетом а . Чему равна высота конуса.
Тест урок 28 Геом. 11кл.
1 вариант
1. Если сфера касается всех граней многогранника, то она называется ..
а) описанной около многогранника
б) вписанной в многогранник
в) касательной к многограннику
2. Все вершины многогранника лежат на сфере , такой многогранник называется ..
а) вписанной в сферу б) описанной около сферы в) касательным к сфере
3. Шар можно вписать в ……
а) произвольную призму б) треугольную пирамиду в) треугольную призму
4. В прямую призму, в основание которой вписана окружность, можно вписать сферу, если..
а) высота призмы равна диаметру вписанной окружности
б) центр сферы лежит на высоте призмы
в) высота призмы равна радиусу вписанной окружности
5. Во всякий цилиндр можно вписать сферу , если ….
а) центр сферы лежит на оси цилиндра
б) сфера касается оснований цилиндра
в) его осевое сечение квадрат
Тест урок 28 Геом. 11кл.
2 вариант
1. Если на сфере лежат все вершины многогранника, то она называется…
а) описанной около многогранника
б) вписанной в многогранник
в) касательной к многограннику
2. Если каждая грань многогранника является касательной плоскостью к сфере, то такой многогранник называется…..
а) вписанным в сферу б) описанным около сферы в) касательным к сфере
3. Шар можно описать около ….
а) любой призмы б) любой правильной пирамиды в) наклонной призмы
4. В прямую призму вписана сфера, около призмы еще описана сфера , центры этих сфер…
а) лежат на разных диагоналях призмы
б) принадлежат высоте призмы и не совпадают
в) совпадают
5. Около любого цилиндра можно описать сферу. Основания цилиндра являются…
а) касательными плоскостями к сфере
б) большим кругом сферы
в) сечениями сферы
Урок 31 Геом. 11 кл.
Тест по теме : Обобщение по теме : Цилиндр, конус, шар.
1 Вариант.
1. Осевое сечение цилиндра- квадрат , длина диагонали которого равна 36см. Найдите радиус основания цилиндра
а) 9см б) 8см в) 8√ 3 см г) 9 √2 см
2. Площадь осевого сечения цилиндра 12√П, а площадь основания равна 64 дм . Найдите высоту цилиндра
а) П/2 дм б) 0,75П дм в) 5П/6 дм г) 3 дм
3. Отрезок СД равен 25 см, его концы лежат на разных окружностях основания цилиндра . Найдите расстояние от отрезка СД до основания , если его высота 7см. а диаметр основания 26см.
а) 6√2 см б) 6 см в) 5см г) 4√3 см
4. Высота конуса равна 4√3 см , а угол при вершине осевого сечения равен 120º . Найдите площадь основания конуса .
а) 120√2 см² б) 136 П см² в) 144 П см² г) 24√3 ∙П см² .
5. Радиус основания конуса равен 7√2 см . Найдите наибольшую возможную площадь осевого сечения данного конуса.
а) 54√2 см² б) 35см² в) 21√2 см² г) 98 см²
6. Отрезок ДЕ хорда основания конуса , которая удалена от оси конуса на 9 см . КО – высота конуса , причем КО= 3√3 см. Найдите расстояние от точки О (центр основания конуса) до плоскости , проходящей через точки Д , Е и К.
а) 4,5см б) 3√2 см в) 3√ 3 см г) 6см
7. Сфера проходит через вершины квадрата СДЕF , стороны которого равна 18см . Найдите расстояние от центра сферы – точки О до плоскости квадрата , если радиус сферы ОЕ образует с плоскостью квадрата угол , равный 30 .
а) 4см б) 4√3 см в) 3√6 см г) 6см
8. Стороны треугольника MKN касаются шара. Найдите радиус шара , если MK =9см, MN=13см, KN=14см и расстояние от центра шара О до плоскости MNK равно √ 6 см .
а) 4√2 см б) 4см в) 3√3 см г) 3√2 см
Урок 31 Геом. 11 кл.
Тест по теме : Обобщение по теме : Цилиндр, конус, шар.
2 Вариант.
1. Радиус основания цилиндра 3, высота8.найдитедиагональ осевого сечения.
2. Радиус сечения цилиндра квадрат, площадь которого 12см². Найдите площадь основания цилиндра.
а) П см². б) 2П см в) 10см² г) 5см²
3. Площадь осевого значения цилиндра равна 10м², а площадь основания 5м². Найдите высоту цилиндра
а) Пм б) 2П м в)√5П м г)√3П м.
4. Высота коеуса равна 15см, а радиус основания равен 8см. Найдите образующую конуса
а) 19см б) 17см в) 13см г) 13√3 см
5. Осевое сечение конуса – прямоугольный треугольник. Найдите площадь этого сечения , если радиус основания конуса равен 5см.
а) 15см² б)13см² в) 19см² г)25см²
6. Шар радиусом 41дм. Пересечен плоскостью , находящейся на расстоянии 9дм от центра.ННайдите площадь сечения .
а) 40П дм² б) 1600П дм² в) 400П дм² г) 50П дм²
7. Найдите площадь сферы, радиус которой равен 6см.
а) 144П см² б) 25√3 П см² в) 360П см² г) 100П см ²
8.Вычислите площадь круга, площадь которого равна площади сферы радиуса 5м.
а) 20м² б) 10м² в) 5м² г) 15м²
Т ест
Цилиндр. Площадь поверхности цилиндра.
Вариант 1
А1. Площадь боковой поверхности прямого кругового цилиндра равна 12π, а высота цилиндра равна 3. Найдите площадь полной поверхности цилиндра.
¤ 1) 24π ¤ 2) 16π ¤ 3) 22π ¤ 4) 20π
А2. Площадь осевого сечения цилиндра равна 10 см2 , площадь основания равна 5 см2 . Вычислить высоту и площадь боковой поверхности цилиндра.
¤ 1)
 ¤ 2)
¤ 2) 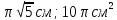 ¤ 3)
¤ 3) 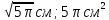 ¤ 4)
¤ 4) 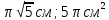
А3. Через образующую цилиндра проведено два сечения, из которых одно осевое с площадью, равной S. Угол между плоскостями сечений равен 30о . Найдите площадь второго сечения.¤ 1)
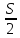 ¤ 2)
¤ 2) 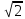 S ¤ 3)
S ¤ 3) 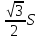 ¤ 4)
¤ 4) 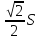
B1. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус основания равен 10 см, расстояние между прямой АВ и осью цилиндра равно 8 см, АВ=13 см. Определите высоту цилиндра.
Ответ:________________________________________________________________________
В2. Высота цилиндра равна h, радиус основания – r. В этот цилиндр наклонно к оси вписан квадрат так, что все его вершины находятся на окружностях оснований. Найдите сторону квадрата.
Ответ:________________________________________________________________________
С1. Диагональ развертки боковой поверхности цилиндра составляет со стороной основания развертки угол β. Вычислите угол между диагональю осевого сечения цилиндра и плоскостью основания.
Ответ:________________________________________________________________________
Т ест
Цилиндр. Площадь поверхности цилиндра.
Вариант 2
А1. Площадь боковой поверхности прямого кругового цилиндра равна 20π, а высота цилиндра равна 5. Найдите площадь полной поверхности цилиндра.
¤ 1) 24π ¤ 2) 32π ¤ 3) 28π ¤ 4) 36π
А2. Площадь осевого сечения цилиндра равна 16 см2 , площадь основания равна 8 см2 . Вычислить высоту и площадь боковой поверхности цилиндра.
¤ 1)
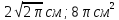 ¤ 2)
¤ 2) ¤ 3)
¤ 4)
А3. Через образующую цилиндра проведено два сечения, из которых одно осевое с площадью, равной S. Угол между плоскостями сечений равен 45о . Найдите площадь второго сечения.¤ 1)
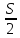 ¤ 2)
¤ 2) 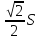 ¤ 3)
¤ 3) 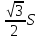 ¤ 4)
¤ 4) 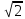 S
S B1. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус основания равен 5 см, высота цилиндра равна 6 см, АВ=10 см. Определите расстояние между прямой АВ и осью цилиндра.
Ответ:________________________________________________________________________
В2. Радиус основания цилиндра равен r . В этот цилиндр наклонно к оси вписан квадрат со стороной a так, что все его вершины находятся на окружностях оснований. Найдите высоту цилиндра.
Ответ:________________________________________________________________________
С1. Угол между диагональю осевого сечения цилиндра и плоскостью его основания равен β. Вычислите угол между диагональю развертки его боковой поверхности и стороной основания развертки.
Ответ:________________________________________________________________________
Т ест
Сфера и шар. Уравнение сферы.
Вариант 1
А1. Точки А и В лежат на сфере радиуса R. Найдите расстояние от центра сферы до прямой АВ, если АВ=m.
¤ 1)
¤ 2)
¤ 3)
¤ 4)
А2. Найдите координаты центра С и радиуса R сферы, заданной уравнением
¤ 1) C (-3; 2; 0), R=
¤ 2) C (3; -2;0), R=5 ¤ 3) C (-3; 2;0), R=5 ¤ 4) C (3; -2;0), R=
А3. Напишите уравнение сферы с центром в точке С (4; -1; 3), проходящей через точку А(-2; 3;1)
¤ 1) ¤ 2)
¤ 3) ¤ 4)
B1. Вершины прямоугольного треугольника с катетами 25 и 5
лежат на сфере. Найдите радиус сферы, если расстояние от центра до плоскости треугольника равно 8.
Ответ:_____________________________________________________________________________
B2. Определите при каких значениях параметра a уравнение
задает сферу.
Ответ:_____________________________________________________________________________
С1. Два взаимно перпендикулярных сечения шара имеют общую хорду длиной 12. Известно, что площади этих сечений 100π и 64π. Найдите радиус шара.
Ответ:_____________________________________________________________________________
Т ест
Сфера и шар. Уравнение сферы.
Вариант 2
А1. Точки А и В лежат на сфере радиуса R. Расстояние от центра сферы до прямой АВ равно a. Найдите длину отрезка АВ.
¤ 1)
¤ 2)
¤ 3)
¤ 4)
А2. Найдите координаты центра С и радиуса R сферы, заданной уравнением
¤ 1) C (-4; 0; 3), R=
¤ 2) C (4; 0;-3), R=7 ¤ 3) C (-4; 0;3), R=7 ¤ 4) C (4; 0;-3), R=
А3. Напишите уравнение сферы с центром в точке С (-3; 1; -2), проходящей через точку А(3; 4;-1)
¤ 1) ¤ 2)
¤ 3) ¤ 4)
B1. Вершины прямоугольного треугольника с катетами 15 и
лежат на сфере. Найдите радиус сферы, если расстояние от центра до плоскости треугольника равно 5.
Ответ:_____________________________________________________________________________
B2. Определите при каких значениях параметра a уравнение
задает сферу.
Ответ:_____________________________________________________________________________
С1. Два взаимно перпендикулярных сечения шара имеют общую хорду длиной 12. Известно, что площади этих сечений 256π и 100π. Найдите радиус шара.
Ответ:______________________________________________________________________
Геометрический тест по геометрии 11кл
урок 42 стр 186
по теме объем фигур
1. В наклонной призме боковое ребро равно 7см, перпендикулярное сечение- прямоугольный треугольник с катетами: 4см, и 3см. Найдите объем призмы.
а) 10см3 б) 42см3 в) 60см3 г) 30см3
2. В правильной шестиугольной пирамиде сторона ее основания 2см, объем пирамиды 6см3. Чему равна высота.
а) √3см б) 3см в) 1/3см
3. Объем пирамиды равен 56см3, площадь основания 14см2. Чему равна высота.
а) 14см б) 12см в) 16см
4. В правильной треугольной пирамиде высота равна 5см, стороны основания 3см. Чему равен объем пирамиды?
а) 15√3/4см3 б) 25√3/2см3 в) 75√3/4см3
5. В правильной четырехугольной пирамиде высота равна 9см. Сторона основания 4см. Найдите объем пирамиды?
а) 50см3 б) 48см3 в) 16см3
6. Объем правильной четырехугольной пирамиды равен 27см3 , высота 9см. Найти сторону основания?
а) 12см б) 9см в)3см
7. Объем усеченной пирамиды равен 210см3, а площадь нижнего основания 36см2, верхнего 9см2. Найдите высоту пирамиды?
а)1см б) 15см в) 10см
8. Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S.
а) 1/3*S б)3*S в)√3S












