Демонстрационный вариант экзамена по дисциплине «Дискретная математика»
Инструкция для студентов
На выполнение письменной работы по математике дается 2 астрономических часа (120 минут).
Экзаменационная работа состоит из двух частей: основной и дополнительной.
При выполнении любого задания требуется предоставить ход решения и указать ответ.
Правильное выполнение задания оценивается баллами. Баллы, полученные за все задания, суммируются.
Критерии оценки выполнения работы:
| Оценка | Число баллов, необходимых для получения оценки
|
| «3» (удовлетворительно) | 9-13
|
| «4» (хорошо) | 14-17
|
| «5» (отлично) | 18-20
|
Основная часть
1. (1балл) Даны множества А={ 4,7,11}, B={1,4,5,7}, U={1,2,3,4,5,9,10,11}. Определите мощность множества 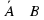 .
.
2. (1 балл) Изобразите с помощью кругов Эйлера множество 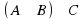 .
.
3. (1 балл) Вычислить 
4. (1 балл) Найти 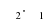 , если
, если  .
.

5. (1 балл) Составьте матрицу смежности, инцидентности для графа
6. (1 балл) Упростите формулу

7. (1 балл) Постройте таблицу истинности формулы 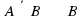 .
.
8. (1 балл) Запишите СДНФ и СКНФ для булевой функции, заданной вектором значений f=(11001010).
9. (1 балл) Запишите суждение в виде формулы логики предикатов: «Не всякое действительное число является рациональным».
10. (1 балл) Для автомата, заданного таблицей, постройте диаграмму Мура
| α / q | 0 | 1 | 2 | 3 |
| 0 | (1;1) | (3;0) | (2;0) | (2;0) |
| 1 | (1;2) | (2;0) | (3;0) | (3;0) |
Дополнительная часть
11. (2 балла) Найдите центр, радиус, диаметр графа:

12. (2 балла) Дано множество 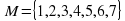 . Составьте матрицу отношения R- « иметь общий делитель, отличный от единицы» определите его свойства.
. Составьте матрицу отношения R- « иметь общий делитель, отличный от единицы» определите его свойства.
13. (2 балла) Докажите, что при любом натуральном n имеет место равенство

14. (2 балла) Исследуйте булеву функцию 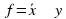 на принадлежность классам Поста.
на принадлежность классам Поста.
15. (2 балл) Составьте МДНФ для булевой функции f(000)=f(001)=f(100)=f(110)=1.







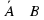 .
.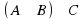 .
.
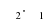 , если
, если  .
. 

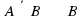 .
.
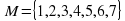 . Составьте матрицу отношения R- « иметь общий делитель, отличный от единицы» определите его свойства.
. Составьте матрицу отношения R- « иметь общий делитель, отличный от единицы» определите его свойства.
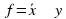 на принадлежность классам Поста.
на принадлежность классам Поста. 



















