Доказательства свойства биссектрисы треугольника

Доказательства свойства биссектрисы угла треугольника

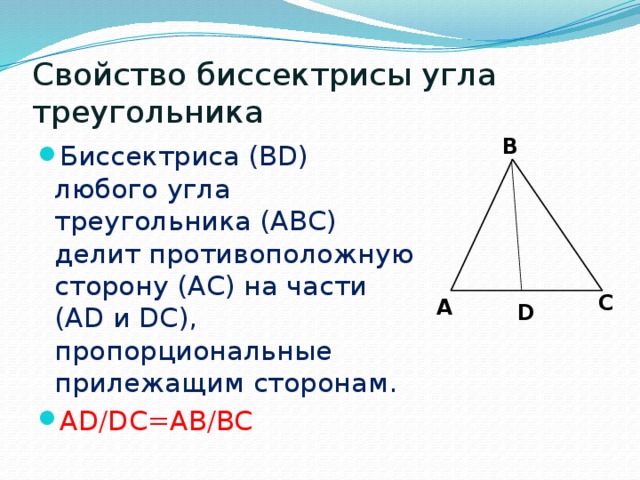
Свойство биссектрисы угла треугольника

B

• Биссектриса (BD) любого угла треугольника (ABC) делит противоположную сторону (AC) на части (AD и DC), пропорциональные прилежащим сторонам.
• AD/DC=AB/BC

C

А

D

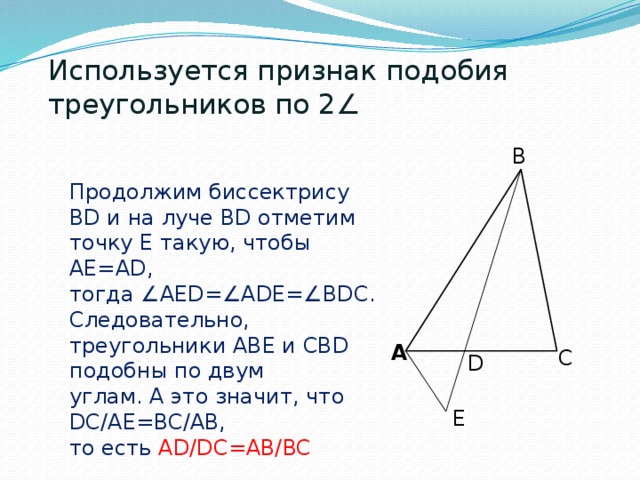
Используется признак подобия треугольников по 2∠

B

Продолжим биссектрису BD и на луче BD отметим точку Е такую, чтобы AE=AD,

тогда ∠AED=∠ADE=∠BDC. Следовательно, треугольники ABE и CBD подобны по двум

углам. А это значит, что DC/AE=BC/AB,

то есть AD/DC=AB/BC

A

C

D

E

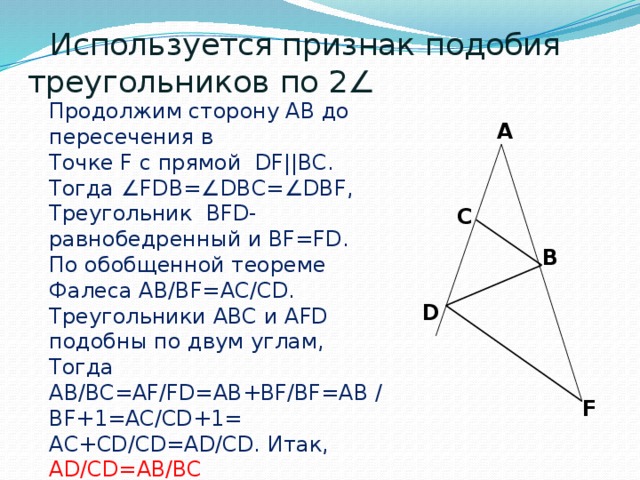
Используется признак подобия треугольников по 2∠

Продолжим сторону AB до пересечения в

Точке F с прямой DF||BC. Тогда ∠FDB=∠DBC=∠DBF,

Треугольник BFD-равнобедренный и BF=FD.

По обобщенной теореме Фалеса AB/BF=AC/CD.

Треугольники ABC и AFD подобны по двум углам,

Тогда AB/BC=AF/FD=AB+BF/BF=AB /BF+1=AC/CD+1=

AC+CD/CD=AD/CD. Итак, AD/CD=AB/BC

A

C

B

D

F

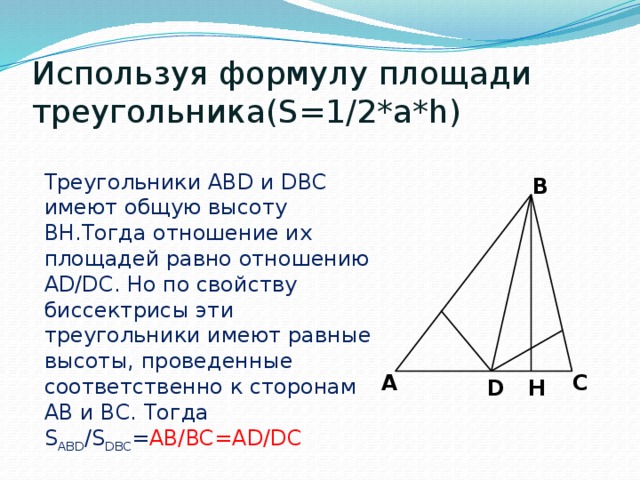
Используя формулу площади треугольника(S=1/2*a*h)

Треугольники ABD и DBC имеют общую высоту BH.Тогда отношение их площадей равно отношению AD/DC. Но по свойству биссектрисы эти треугольники имеют равные высоты, проведенные соответственно к сторонам AB и BC. Тогда S ABD /S DBC = AB/BC=AD/DC

B

A

C

H

D

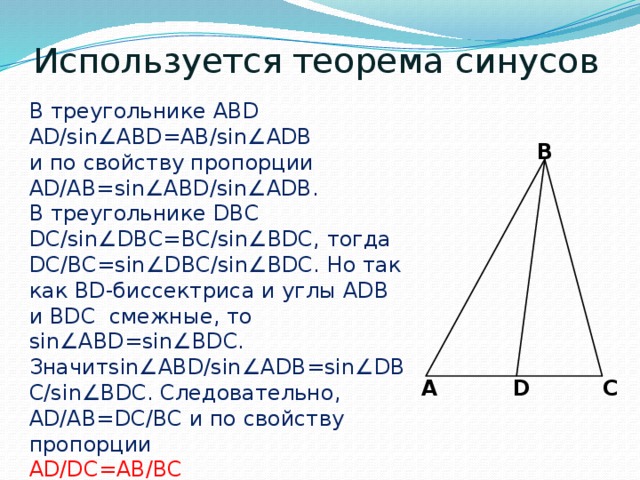
Используется теорема синусов

В треугольнике ABD AD/sin∠ABD=AB/sin∠ADB

и по свойству пропорции AD/AB=sin∠ABD/sin∠ADB.

В треугольнике DBC DC/sin∠DBC=BC/sin∠BDC, тогда

DC/BC=sin∠DBC/sin∠BDC. Но так как BD-биссектриса и углы ADB и BDC смежные, то sin∠ABD=sin∠BDC.

Значитsin∠ABD/sin∠ADB=sin∠DBC/sin∠BDC. Следовательно, AD/AB=DC/BC и по свойству пропорции

AD/DC=AB/BC

B

A

C

D

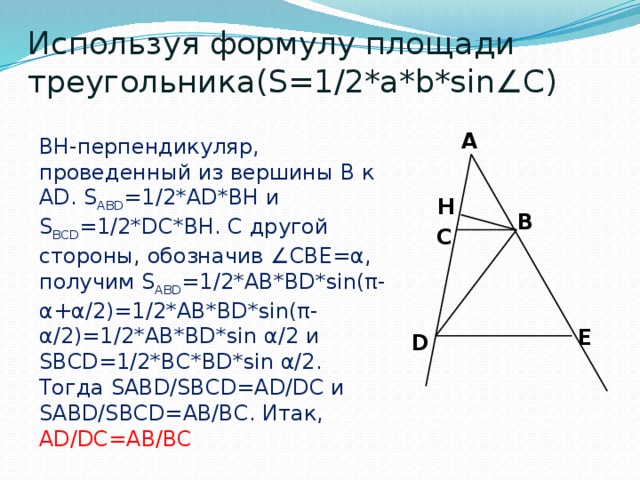
Используя формулу площади треугольника(S=1/2*a*b*sin∠C)

A

BH-перпендикуляр, проведенный из вершины B к AD. S ABD =1/2*AD*BH и S BCD =1/2*DC*BH. С другой стороны, обозначив ∠CBE=α, получим S ABD =1/2*AB*BD*sin(π-α+α/2)=1/2*AB*BD*sin(π-α/2)=1/2*AB*BD*sin α/2 и SBCD=1/2*BC*BD*sin α/2. Тогда SABD/SBCD=AD/DC и SABD/SBCD=AB/BC. Итак, AD/DC=AB/BC

H

B

C

E

D