Методическая разработка
«Доказательство неравенств во внеклассной работе со школьниками»
Автор: Морозова В.А.,
учитель математики
МБОУ «СОШ-ДС № 37 им. И.Г.Генова»
Симферополь, 2022
Содержание
Введение…………………………………………………………………………...3
1.Свойства и основные методы доказательства неравенств…………………...6
2.Доказательство неравенств с помощью рассмотрения разности частей и алгебраических преобразований………………………………………………....8
3.Использование известных неравенств………………………………………10
3.1 Неравенство Евклида (8-9 класс)…………………………………………10
3.2 Неравенство Коши (9-10 класс)…………………………………………..13
3.3 Неравенство Бернулли (9-10 класс)…………………………..………….18
3.4 Неравенство Коши- Буняковского (10-11 класс)……………………..…22
3.5 Неравенство Йенсена (11 класс)……………………………………….....25
4.Метод математической индукции ( 8-9 класс)…………………………...….27
5.Метод «оценка+ пример» (8-11класс)……………………………………......29
6.Самостоятельно составленные задачи…………………………………….....33
Заключение……………………………………………………………………….36
ВВЕДЕНИЕ
Задачи на доказательство неравенств занимают очень важное место для математической подготовки учеников. Учащиеся знакомятся с понятием неравенство еще в младшей школе , изучая отношения "больше", "меньше", "равно" и учатся записывать результаты сравнения с помощью знаков , а так же читать полученные неравенства. Далее школьники встречаются с понятием неравенство в 5-6 классах. Они встречаются с такими заданиями:
Какая из точек лежит левее на координатном луче …
Запишите с помощью двойного неравенства.
Я задумала число, оканчивающееся на 5. Оно больше 210 и меньше 220. Назовите его…
Ближе всего знакомятся с доказательством неравенств учащиеся в 8 классе. В рабочей программе по алгебре для 8 класса особое внимание уделяют на следующие темы: «Числовые неравенства и их свойства», «Линейные неравенства с одной переменной», «Системы неравенств с одним неизвестным». Все приобретенные учащимися навыки находят применение при изучении тем «Решение квадратичных неравенств».
Обучающиеся должны знать, хотя бы три способа для решения квадратичных неравенств:
1. На основе разложения квадратного трехчлена на множители, построение эскиза графика квадратного трехчлена и написать ответ.
2. На основе разложения квадратного трехчлена на множители, использовать метод интервалов.
3. Графический метод решения неравенства: ах2 + вх +с0 ; ах2 - вх – с.
После детального изучения школьной программы , в части на доказательства неравенств ,учащиеся могут узнать намного больше интересных и познавательных задач на внеурочной деятельности.
Неравенства данной темы решаются алгебраическим способом, который является одним из лучших средств саморазвития , логического мышления. Благодаря специально подобранным задачам, которые способны заинтересовать учащихся своей кажущейся простотой и тем, что их решение не сразу дается в руки, можно показать учащимся красоту, простоту и изящество логического рассуждения. Задачи на обычно решаются способами. Это повод привлечь любопытство найти , как самый простой , но и на такие , которые часто используются при решении самых разных задач.
разрешают воплощать в развитие изучения темы таких заданий: формирование навыков составления алгоритма выполнения; определение последовательности промежуточных целей с учетом конечного результата, помогают выполнять простейшие преобразования, излагать выводы; мысли.
В моей методической разработке рассмотрены следующие виды задач:
1. Доказательство неравенств с помощью рассмотрения разности его частей и алгебраических преобразований.
2. Задачи на доказательства с использованием уже доказанных неравенств (неравенство Коши, Коши-Буняковского, Йенсена и др.)
3. Метод математической индукции.
4. Метод «оценка + пример».
Например, доказывать неравенства с помощью математической индукции и Неравенством Евклида можно ученикам 8 класса на внеклассных занятиях.
Неравенства Коши и Неравенства Бернулли рассматривать уже в 9 классе, когда учащиеся владеют достаточными знаниями по данной теме.
С Неравенством Коши-Буняковского можно познакомить учащихся в 10 классе на внеклассной работе. А с Неравенством Йенсена в 11 классе, так как понятие производной в школьном курсе алгебры вводится только в 11 классе. Все вышеперечисленные виды неравенств играют большую роль в курсе алгебры.
Данная разработка рассчитана на учащихся, которые имеют довольно-таки высокий уровень знаний в области математики, причем как в пределах, так и вне школьной программы, но все равно хотят его повысить.
1. и методы .
неравенств:
К неравенства или отнять
 f(x) ) ) + h(x) )+ )
f(x) ) ) + h(x) )+ )
Неравенства можно :
 f(x) )
f(x) )
p(x) h(x) ) + p(x) g(x)+ )
разных почленно :
 ) g(x)
) g(x)
) g(x)- )

Можно умножать и делить на одно и тоже положительное число обе части неравенста:
) g(x) a·f(x) a·g(x) , a 0
В случае, когда обе неравенства , либо умножить на и тоже , неравенства изменится на :
 ) g(x) a·f(x) a·g(x) , a
) g(x) a·f(x) a·g(x) , a
О доказательства :
Доказать неравенство - это значит обосновать его истинность при всех допустимых значениях переменных.
Существуют различные методы доказательства неравенств:
1. Рассмотрение разности левых и правых частей.
2. Рассмотрение частного и сравнение с единицей.
3. Метод от противного.
4. Использование уже доказанных неравенств.
2. Доказательство неравенств с помощью рассмотрения разности его частей и алгебраических преобразований.
Задача 1. (Окружной этап всероссийской олимпиады для 9 класса 1992-1993 учебный год)
Докажите, что верно неравенство x2 + xy + y2 ≥ 3(x + y − 1), для любых действительных чисел x и y.
Доказательство:
Разберем данное выражение как квадратный трехчлен относительно x:
x2 + xy + y2 - 3(x + y − 1) = x2 + (y − 3)x + (y2 – 3y + 3)
Посчитаем дискриминант и получим:
−3(y− − 1)2
Итак, дискриминант отрицателен.
Трехчлен допускает только положительные значения и показатель  0, следовательно x2 +xy+y2 ≥ 3(x+y−1) при любых x и y. Равенство верно, когда x = y = 1.
0, следовательно x2 +xy+y2 ≥ 3(x+y−1) при любых x и y. Равенство верно, когда x = y = 1.
Задача 2. (Белорусская республиканская олимпиада, 9 класс 1962-1963 учебный год )
Докажите, что наибольшая площадь треугольника равна 1, стороны которого a, b, c заключены в пределах: 0x 1y2z3 ?
Доказательство:
Площадь треугольника находим по формуле: S =  xy·sin𝝰
xy·sin𝝰
Среди треугольников со сторонами x, y, удовлетворяющими условию задачи наибольшую площадь имеет прямоугольный треугольник с катетами x = 1 и y = 2. Третья сторона z  удовлетворяет условию задачи, следовательно указанный треугольник имеет наибольшую площадь среди всех рассматриваемых. Следовательно площадь треугольника равна 1.
удовлетворяет условию задачи, следовательно указанный треугольник имеет наибольшую площадь среди всех рассматриваемых. Следовательно площадь треугольника равна 1.
Задача 3.
F(x) — квадратный трехчлен с показателями больше нуля.
Докажите, верно неравенство: (F(xy))2 ≤ F(x)2 F(y)2.
Доказательство:
Пусть F(x)= ax2+bx+c. Тогда (F(xy))2-F(x2)F(y2)= (ax2y2+bxy+c)2- (ax4+bx2+c)(ay4+by2+c)= a2x4y4+b2x2y2+c2+2abx3y3+2acx2y2+2bcxy-a2x4y4-b2x2y2-b2x2y2-c2-abx2y2(x2+y2)-ac(x4+y4)-bc(x2+y2)=abx2y2(2xy-x2-y2)+ac(2x2y2-x4-y4)+bc(2xy-x2-y2)=-abx2y2(x-y)2-ac(x2-y2)2-bc(x-y)2
При a ≥ 0, b ≥ 0, c ≥ 0 данные слагаемых отрицательны, следовательно неравенство (F(xy))2 ≤ F(x)2 F(y)2.
3. Использование известных неравенств.
Основные неравенства, на которые опираются при доказательстве других неравенств:
3.1 Неравенство Евклида (8-9 класс)
 ≥
≥  , при
, при  ≥ 0
≥ 0
 -
-  =
=  =
=  ≥ 0
≥ 0
Следовательно,  ≥
≥ 
Равенство достигается, тогда и только тогда, когда числа  равны.
равны.
Рассмотрим задачи на неравенство Евклида:
Задача 1.
Доказать, что  +
+  ≤
≤  для a, b 0
для a, b 0
Доказательство:
Возведем обе части в квадрат:
 +
+  +
+ ≤
≤ 
Далее, приведем к общему знаменателю и раскроем скобки, получим:
2(1 + a2 + b2 + a2b2) −(1 + b2 + ab + ab3) −(1 + a2 + ab + a3b) = (1 −ab)(a − b)2 ≥ 0
Из неравенства Евклида о средних для двух чисел имеем:
 ≤
≤  +
+  ≤
≤ 
Сложив полученные неравенства, получаем что что  +
+  ≤
≤ 
Задача 2.
Доказать, что для положительных чисел а, b и с:
(a+b)(b+c)(c+a)  8abc
8abc
Доказательство:
Согласно тому, что  .
.
Если мы перемножим оба неравенства, то получим, что (a+b)(b+c)(c+a)  8abc
8abc
Задача 3.
Доказать, что если x 0, y 0, z 0, то  +
+  +
+  ≥ 3
≥ 3
Доказательство:
Введем замену переменных:
a= y+z
b= x+z
c= y+x;
Выразим переменные:
2x = −  +
+  +
+ 
2y =  −
−  +
+ 
2z =  +
+  −
−  .
.
Получаем неравенство
 +
+  +
+  ≥ 3
≥ 3
 +
+  +
+  ≥ 6
≥ 6
Мы видим, что все три скобки больше или равны двум. Следовательно , левая часть неравенства больше или равна шести.
3.2 Неравенство Коши (9-10 класс)
К числу наиболее часто встречающихся в математике числовых неравенств относится неравенство: «среднее арифметическое двух или более неотрицательных чисел больше или равно их среднему геометрическому», которое носит название Неравенство Коши:


 ,
, ,
,  ≥ 0
≥ 0
Рассмотрим задачи на Неравенство Коши:
Задача 1.
Доказать неравенство: (1+a)(1+b)(1+c) ≥ 8(1-a)(1-b)(1-c), при этом a+b+c=1
Доказательство:
Так как, по условию a+b+c=1, значит 1+a=(1-b)+(1-c).
Далее, применим неравенство Коши между средним арифметическим и средним геометрическим x + y ≥2 , получим:
, получим:
1+ a ≥ 2  .
.
1+b ≥ 2  .
.
1+c ≥ 2  .
.
Теперь, если мы перемножим данные неравенства, то увидим ,что (1+a)(1+b)(1+c) ≥ 8(1-a)(1-b)(1-c).
Задача 2.
Докажите, что для любого натурального n  2 имеют место неравенства n
2 имеют место неравенства n
 +…+
+…+ n
n +1
+1
Доказательство :
Применим неравенство между средним арифметическим и средним геометрическим для чисел 2,  ,
,  ,..,
,.., . В результате получим:
. В результате получим:

 , т.е
, т.е

 Применим неравенство между средним арифметическим и средним геометрическим для чисел 2,
Применим неравенство между средним арифметическим и средним геометрическим для чисел 2,  ,
,  ,..,
,.., . В результате получим :
. В результате получим :

 , т.е
, т.е

Задача 3.
Доказать, что для любых четырех действительных чисел a, b, c, d выполняется неравенство:
 ≥ 4abcd
≥ 4abcd
Доказательство :
Применим неравенство Коши между средним арифметическим и средним геометрическим, получим:
 ≥
≥ 
Следовательно,  ≥ 4abcd
≥ 4abcd
Задача 4.
Для положительных чисел a, b, c доказать неравенство:
 +
+  +
+  ≥ 3
≥ 3
Доказательство :
Перепишем данное неравенство в виде: 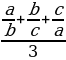 ≥ 1
≥ 1
Выражение в левой части – это среднее арифметическое трех чисел 
 ,
, 
 ,
, 
 .
.
Среднее геометрическое этих чисел равно:

Наше неравенство сводится к неравенству для среднего арифметического и среднего геометрического трех указанных чисел.
Следовательно,  +
+  +
+  ≥ 3
≥ 3
Задача 5.
Докажите, что  ≥ 2, если a + b = 2.
≥ 2, если a + b = 2.
Доказательство:
Введем замену переменных a: a = 1 − x, тогда , b = 1 + х.
Следовательно,  = 2 + 12
= 2 + 12 + 2
+ 2 ≥ 2.
≥ 2.
А значит  ≥ 2.
≥ 2.
Задача 6. ( Сборник ЕГЭ профильный уровень 2018 год)
Доказать неравенство:
 ≤
≤ 
Доказательство:
В данном неравенстве мы видим формулы квадрата суммы и квадрата разности, введем замену переменных : a =  ,b =
,b =  .
.
Тогда получим:
a+b=  =
= 
Данное неравенство принимает вид:
 +
+ ≤
≤  , откуда
, откуда  +
+ - 2ab ≤ 0
- 2ab ≤ 0
Неравенство верно, при условии, если a=b.
Следовательно:
 =
=
Выполним умножение крест-накрест и получим:
 x =
x =
Ответ: x = 
Задача 7. ( Сборник ЕГЭ профильный уровень 2018 год)
Доказать неравенство:



Доказательство:
Избавимся от знаменателя до множив обе части на 4, получим:
2 + 8
+ 8 ≤
≤ 
Далее раскроим скобки и формулы квадрата суммы и квадрата разности:
2 - 4x+2+8
- 4x+2+8 + 16x+8 ≤ 9
+ 16x+8 ≤ 9 +6x+1
+6x+1
Приведем подобные слагаемые:
 +6x+9≤ 0
+6x+9≤ 0
Отсюда видно, что дискриминант равен 0, следовательно неравенство имеет один единственный корень:
x= -3
Ответ: -3.
3.3 (9-10 )
, записанное в :
 ≥ 1+ nx
≥ 1+ nx
неравенством . Это выполняется при x ≥ -1 и для n ≥ 1. Доказательство на методе .
Очевидно, что при n=1 выполняется. выполняется при n1. Проверим неравенства при n+1:
 = (1+)
= (1+)  ≥ (1+ x)(1++
≥ (1+ x)(1++ ≥1+(n+1)x
≥1+(n+1)x
выполняется и значениях n, чем 1. При положительных n, меньше чем 1, неравенство:
 ≥ 1+ nx, 10.
≥ 1+ nx, 10.
Рассмотрим задачи на неравенство Бернулли:
1.
Решить :
 +
+  = 2
= 2
Решение:
Используя неравенство Бернулли получаем:
 +
+  ≤ 1+
≤ 1+ 
 + 1-
+ 1- 
 = 2
= 2
Решение неравенства достигается тогда и только тогда, когда  , то есть
, то есть
x = 1, x = -1.
Ответ: 1,-1.
2.
: (1 + 𝝰)n ≥ 1 + n𝝰, где 𝝰 -1, n – число.
:
методом .
При n = 1 получаем :
1 + α ≥ 1 + α.
Предположим, что неравенство:
(1 + α)n ≥ 1 + nα.
(1 + α)n+1 ≥ 1 + (n + 1)α.
Мы видим, что 𝝰 -1 и 𝝰 +1 0.
Умножим левую и правую часть неравенства на (a + 1) , получим:
(1 + 𝝰)n (1 + 𝝰) ≥ (1 + 𝝰)(1 + 𝝰)
Так как n ≥ 0, то
≥ 0, то
(1 + 𝝰)n+1 ≥ 1 + (n + 1)𝝰 + n𝝰 ≥ 1 + (n + 1)𝝰.
Следовательно, (1 + 𝝰)n ≥ 1 + n𝝰.
3.
Дано: a1 + a2 + . . . + an ≤  , где a1, a2, . . . , an - положительные числа.
, где a1, a2, . . . , an - положительные числа.
Доказать, что (1 + a1)(1 + a2) . . . (1 + an)
(способ 1):
Итак, для начала раскроем скобки в левой части неравенства, получим:
1 + (a1 + . . . + an) + (a1a2 + . . . + an-1an) + (a1a2a3 + ...+ an-2 an-1an) + . .+ a1a2 . . +an.
Мы видим, что во второй скобке неравенства ,сумма чисел не превосходит:
( + . . . +
+ . . . +  )2, аналогично и в не превосходит (
)2, аналогично и в не превосходит ( +….+
+….+ )3.
)3.
Отсюда следует, что 1 +  +
+  +
+  + . . . +
+ . . . +  = 2 –
= 2 – 
2.
Методом докажем, что для n неравенство:
(1 + a1) . . . (1 + an) 1 + . . . + an).
При n = 1 : 1 + a1 1.
при n = k имеет : (1 + a1) ….(1 + ak) 1 +….+ ak).
случай n = k +1 + a1) . . . (1 + ak)(1 + ak+1)
+ 2(a1 + . . . + ak)) ·(1 + ak+1) ≤ 1 + 2·(a1 + . . . + ak) + ak+1 ·(1 + 2 · ) =
) =
= 1 + 2·(a1 + . . . + ak + ak+1).
В математической доказано.
4.
, что если  то неравенство
то неравенство 
:
Из , что  , следует, что
, следует, что  с очевидным :
с очевидным : 
: 
Возведя обе неравенства в , :  Сложив с неравенством:
Сложив с неравенством: 


Сложив эти с неравенством 

5. (Окружной олимпиады для 9 19945 учебный год)
Докажите, :
 +
+ ≤
≤ 
Доказательство:
Из неравенства видно, что
 +
+ 2
2 a.
a.
 +
+ ≤
≤ 

Задача 6. (Окружной олимпиады для 9 19945 учебный год)
Доказать:  +
+  +
+  x + y + z.
x + y + z.
:
По │x-y│x2 -2xy+ y2 x2 +2xy+y2 xy), следовательно x+y  , так как x и y . , y+z
, так как x и y . , y+z  , z+x
, z+x  , следовательно x + y + z
, следовательно x + y + z  +
+  +
+  .
.
7. ( этап для 11 класса 1993-1994.)
, что при всех x, 0  , sin2x + 1.
, sin2x + 1.
Доказательство:
Используем следующие тригонометрические тождества:
1- cosx = 2 sin2  , sin2x = 4sin
, sin2x = 4sin  cos
cos  ,
,
Данное неравенство приведем к следующему виду: 2 tg  .
.
Отсюда следует, что 2 2 cos  = 1 , а значит tg
= 1 , а значит tg 
 Таким образом sin2x + 1.
Таким образом sin2x + 1.
3.4 Неравенство Коши- Буняковского (10-11 класс)
Теорема. Для любых наборов чисел:  ,
, ,
,
 ,
,  ,
,
Верно неравенство:
│ +
+  │ ≤
│ ≤  ·
·  (1)
(1)
 ≤
≤ 
Рассмотрим функцию:
f (t) =  +
+ 
t – переменная , остальные-параметры.
f(t) = 

 +
+  = A
= A – 2Ct + B.
– 2Ct + B.
A = 0 тогда и только тогда, когда  =
= =
= = 0 и неравенство (1) очевидно.
= 0 и неравенство (1) очевидно.
A ≠ 0 тогда и только тогда, когда A 0 и f – квадратичная функция с графиком возрастающим вверх.
Так как , f(t) ≥ 0, то уравнение f(t) = 0 имеет не более одного корня и дискриминант меньше или равен нулю.
D = 4 – 4 AB = 4
– 4 AB = 4  ≤ 0 , то есть
≤ 0 , то есть  ≤ AB.
≤ AB.
Замечание. Во многих задачах , важным является несколько само неравенство Коши-Буняковского, сколько условие равенства в этом неравенстве.
Равенство в неравенстве (1) может достигаться тогда и только тогда, когда существует  : f (
: f ( ) = 0.
) = 0.
 +
+  + ….+
+ ….+  = 0.
= 0.
 =
=  =
=  =
= 
Так же можно сказать ,что равенство будет соблюдаться , если хотя бы один из двух числовых наборов является вырожденным:
 =
= =
= = 0
= 0
 =
= =
= = 0
= 0
Задача 1.
Дано: x+y+z = 1.
Доказать, что x2 + y2 + z2 ≥ 
Доказательство:
Согласно неравенству Коши-Буняковского:
1 = 1·x + 1·y + 1·z ≤  ·
·  =
= 

Следовательно x2 + y2 + z2 ≥  .
.
Задача 2.
Доказать, что 
Доказательство:
На основе применения неравенства можно записать, что
 ≤
≤ 

Так как  =55, то
=55, то  ≤ 550
≤ 550
Или  ≤
≤  .
.
Задача 3.
Известно, что  +
+ 
 = 1.
= 1.
Найти: min ( 3x + 4y+5z)
max( 3x + 4y+5z)

 Решение:
Решение:
│( 3x + 4y+5z)│ ≤ 
 =
=  = 5
= 5
- 5 ≤ 3x + 4y+5z ≤ 5
≤ 3x + 4y+5z ≤ 5 .
.
Чтобы сделать вывод, что - 5 и 5
и 5 искомые значения , необходимо найти x, y, z для которых они достигаются. Это можно сделать с помощью условий неравенства Коши-Буняковского:
искомые значения , необходимо найти x, y, z для которых они достигаются. Это можно сделать с помощью условий неравенства Коши-Буняковского:
 =
=  =
= 
 +
+ 
 = 1.
= 1.
y = x
x
z =  x
x
 +
+  +
+  = 1
= 1
 =
= 
Отсюда, x = ± 
Если выбирать знак «+» , то будет достигаться max значение, если знак «-» , то min значение.
Ответ: min - 5 , max 5
, max 5 .
.
 3.5 Неравенство Йенсена (11 класс)
3.5 Неравенство Йенсена (11 класс)
Рассмотрим еще такой общий подход к доказательству неравенств с использованием свойств выпуклости ( вогнутости) функций. Хорошо известно , что для всякой выпуклой (вогнутой) функции f : [a;b] R будет верно неравенство Йенсена:
f ( +..+
+..+ ) ≤
) ≤  +…+
+…+  (1)
(1)
f ( +..+
+..+ ) ≥
) ≥ +…+
+…+ 
 ,
,  ,…,
,…,  € [a;b];
€ [a;b];
 +…+
+…+  = 1
= 1
 0
0
Выпуклость (вогнутость) функций удобно проверять с помощью второй производной f, если f достаточно гладкая:
f ′′ (x) 0
f ′′ (x) x € [a;b];
Проверить выпуклость (вогнутость) f, можно на базе (1).
Задача.
Доказать неравенство:
 ≤
≤ 
Доказательство:
Пусть f(x) = ln sin  .
.
Для проверки вогнутости f , найдем f ′′ (x):
f ′′ (x) = 
 ′ =
′ = 
 ·
· 
 ,
, ,ɤ- углы треугольника.
,ɤ- углы треугольника.
Т.е  +
+ +ɤ=180◦
+ɤ=180◦
f  ≥
≥  (f(
(f( )+f(
)+f( )+f(
)+f( ))
))
ln sin 60◦  ln sin
ln sin  sin
sin  sin
sin 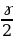
3ln ≥ln..
≥ln..
ln  ≥ ln sin
≥ ln sin
sin  sin
sin  sin
sin 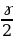 ≤
≤ 
 = 3
= 3 ≥ ln
≥ ln
Следовательно,  ≤
≤  .
.
4.Метод математической индукции ( 8-9 класс)
Индукция – это рассуждение от частного к общему.
Метод математической индукции удобно применять ,если требуется доказать какую-то последовательность утверждений  . И оказывается , что доказательство этой последовательности равносильно доказательству всего двух таких утверждений:
. И оказывается , что доказательство этой последовательности равносильно доказательству всего двух таких утверждений:
1) базис:  .
.
2) для любого k из  следует
следует 
В некоторых задачах шаг 2) заменяют на следующий: если верно  , при l ≤ k , то верно
, при l ≤ k , то верно  .
.
шаг 1) называют базисом индукции.
шаг 2) индуктивным переходом.
С методом математической индукции учащихся знакомят в 9-10 классе.
Докажем несколько неравенств методом математической индукции:
Задача 1.
Найдите все n € N : 
 , n= 1,2,3…
, n= 1,2,3…
Докажем, при n ≥ 5 , 
 ;
;
1. Базис  = 32
= 32  = 25
= 25
2. Пусть при n=k : 

3. Докажем, при n = k+1 : 

 = 2·
= 2·



 =
= 
 – 2k -1 =
– 2k -1 =  – 2k-1=
– 2k-1=  - 2k + 1- 2=
- 2k + 1- 2=  – 2.
– 2.
Так как k ≥ 5, то  ≥ 16 2.
≥ 16 2.
Следовательно, 
 .
.
Ответ: при n=1, а так же n ≥ 5.
Задача 2.
Доказать, что для любого n € N, n ≥2 : ab ≥ 0.
 +
+ 


Доказательство :
1. Базис : n=2:
2( ) ≥
) ≥  – верно.
– верно.
2. Пусть n=k:
 (
( ) ≥
) ≥ 
3. Докажем, что n=k+1:
 (
( ) ≥
) ≥ 
 = (a+b)
= (a+b) ≤
≤  · (a+b) · (
· (a+b) · ( ) =
) =  · (
· ( +a
+a +
+ +
+  ·
· – (a
– (a +
+ ) =
) =  -
-  +
+  - a
- a =
=  (a-b) +
(a-b) +  (b-a) = (a-b)
(b-a) = (a-b) ).
).
При ab , следует, что  , значит (a-b)
, значит (a-b) ) 0.
) 0.
При ab , следует, что  , значит (a-b)
, значит (a-b) ) 0.
) 0.
a +
+ ≤
≤  .
.
5.« плюс » класс)
« пример» — это рассуждение, используется в для определения наибольших и . Смысл метода «оценка плюс пример» заключается в том , что требуется не только установить неравенство , но еще и показать его неулучшаемость и привести пример , когда достигается равенство.
Данный метод осуществляется следующим образом:
1. Оценка. Убеждаемся , что данное неравенство выполняется: B ≥ 𝝰
2. . Показываем пример, при котором равенство B = 𝝰
Задача 1.
100 . Со всех аэродромов взлетает самолет и на к нему . Все различны. , что ни на аэродром не шесть .
:
Предположим, что из M и N прилетели в P , расстояние MN- треугольника MPN и  MPN 60◦. Так же , что в P прилетели из
MPN 60◦. Так же , что в P прилетели из  ,….
,….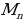 . Отсюда , что из углов
. Отсюда , что из углов  P
P не
не  .
.  60◦ , получаем .
60◦ , получаем .
2.
В конкурсе « » участвовало 7 . кондитер по два . В конце , что призов не и все держав в по два бросили их в . Какое кондитеров с «незапятнанной »?
:
Выберем между расстояние. Они по два в соседей. Так как , то кондитеры в друга по . Поскольку еще по одному , то эти попали в еще из . Итак, не кондитеров .
возможна , все торты в кондитеров. произойти , кондитера в виде , а трое находиться прямоугольника собой . данного :

5
6 7
1 2


3 4
на рисунок , что четверо , находятся прямоугольник с « репутацией».
 3.
3.
 x+
x+ x = 1
x = 1
, что  x ≤
x ≤ x
x
 x ≤
x ≤ x
x
Доказательство:
1= x +
x + x ≤
x ≤  x+
x+ x=1
x=1
 x =
x = x
x
 x =
x = x
x

 cos x = 0 или cos x =1, k€Z x=
cos x = 0 или cos x =1, k€Z x= +2π , k€
+2π , k€
sin x = 0 или cos x = 0
cos x =1 sin x =1
Следовательно,  x ≤
x ≤ x
x
 x ≤
x ≤ x
x
Задача 4. (Сборник ЕГЭ профильный уровень)
Имеется более 40, но 48 чисел. этих –3, среднее положительных из них 4, а арифметическое из них равно –8.
а) имеется?
б) чисел : положительных или ?
в) наибольшее чисел среди ?
:
Начнем задачи с : пусть x, отрицательных y, а z. найдем чисел: , всех их количеству , умноженному на . Определим :
4x −8y+ 0⋅z = − 3(x + y +z)
пункт а):
Мы , что в равенстве каждое из на 4, следовательно x+y+z будет делиться на 4. По условию число удовлетворяет :
40 x + y + z
x + y + z = 44, т.к. единственное между 40 и 48, на 4- это 44.
Ответ на а) : 44 написано на .
пункт б):
Для каких больше: или приведем :
4x −8y = − 3(x + y +z) его:
5x = 7y + 3z.
Рассмотрим в):
наибольшее чисел среди ?
Мы , что 5x ≥ 7y,x y. Следовательно записано , чем . Далее 44 вместо в :
4x −8y = − 3(x + y+ z).
4x −8y = − 3 · 44
4x −8y = − 132
x= 2y – 33
Видно, что x+y ≤ 44, :
3y − 33 ≤ 44
3y ≤ 77
y = 25
Значит x= 2y - 33 ≤ 17. количество 17.
Ответ: а) 44; б) ; в) 17.
6.Самостоятельно составленные задачи
 Задача1.
Задача1.
Решить уравнение:
 +
+  =
=  +
+ 
 ·
· +
+  · 4 ≥
· 4 ≥  +
+ 
Ведем замену:
x - 2 = t
2 – x = -t
Получим:
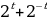 =
=  +
+ 
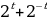 = 2
= 2
 +
+  = 2
= 2
x - 1 + 3 – x + 2 = 4
= 4
2 = 2
= 2
 = 1
= 1
(x-1)(3-x) = 1
3x - – 3 + x – 1= 0
– 3 + x – 1= 0
- + 4x – 4 = 0
+ 4x – 4 = 0
 – 4x + 4 = 0
– 4x + 4 = 0
 = 0
= 0
x = 2, следовательно t=0.
Ответ: x = 2.
Задача 2.
1 +  πx =
πx =  +
+ 
1 ≤ 1 +  πx ≤ 2
πx ≤ 2
 +
+  ≤
≤  ·
·  = 2
= 2
3 ≤ x ≤ 6
При x = 4 ( Из условия равенства в неравенстве Коши-Буняковсекого для корней)
Получаем:
1 +  4π = 2
4π = 2
 +
+  = 2.
= 2.
Ответ: 2.
Задача 3.
Доказать неравенство:
10 + 2
+ 2 + 5
+ 5 ≥ 2xy + 4yz + 6xz
≥ 2xy + 4yz + 6xz
 – 2xy +
– 2xy + +
+  – 4yz + 4
– 4yz + 4 +
+  – 6xz + 9
– 6xz + 9 ≥ 0
≥ 0
Свернем данное неравенство в квадрат разности, получим:
 +
+  +
+  ≥ 0
≥ 0
Следовательно , 10 + 2
+ 2 + 5
+ 5 ≥ 2xy + 4yz + 6xz.
≥ 2xy + 4yz + 6xz.
Задача 4.
Решить уравнение:
 +
+  = │x - 2│ + │x - 4│
= │x - 2│ + │x - 4│
Решение:
ОДЗ x € [ 2;4 ]
Докажем, что левая часть меньше или равна 2:
 +
+  ≤ 2
≤ 2
Из неравенства Коши-Буняковского, получаем:
1· + 1 ·
+ 1 · ≤
≤  +
+  = 2 (*)
= 2 (*)
Докажем, что правая часть больше или равна 2:
│x - 2│ + │x - 4│= │2 - x│ + │x - 4│≥ │2 – x + x - 4│= 2
Так как, │a + b│ ≤ │a│ + │b│ для любых a и b.
Итак, левая часть не больше 2, а правая – не меньше 2. Поэтому  +
+  = │x - 2│ + │x - 4│= 2. Это означает, что в (*) достигается равенство , что возможно только при x – 2 = 4 – x = 1 или x = 3.
= │x - 2│ + │x - 4│= 2. Это означает, что в (*) достигается равенство , что возможно только при x – 2 = 4 – x = 1 или x = 3.
Проверка показывает, что x = 3 подходит.
Ответ: x = 3.
Заключение
В результате проделанной работы был подобран материал по теме «Доказательство неравенств во внеклассной работе со школьниками», а именно: теоретические сведения по неравенствам Йенсена, Коши, Коши-Буняковского и Бернулли, задачи, в решениях которых используются эти неравенства.
На основании выбранной учебной и методической литературы были выделены основные моменты, связанные с проведением школьных математических олимпиад. Подробно раскрыты цели и структура олимпиад по математике в школе. Сделан вывод, что математические олимпиады являются достаточно популярной формой организацией внеурочной работы в школе. Раскрыто содержание теоретических вопросов, связанных с понятиями и методами решений неравенств, также рассмотрены основные классические неравенства, которые используются при решении задач математических олимпиад. Все это было собрано и оформлено в виде электронного учебника. Учебник позволяет самостоятельно изучать эту тему, получая знания на достаточном уровне, а также помогает строить логические цели рассуждения; делать выводы о выборе решения, анализировать и оценивать полученные результаты.
Список литературы
1. Выгодский М.Я. Справочник по элементарной математике. – М.: Наука, 1972. – 416 с.
2. Ижболдин О., Курляндчик Л. Неравенство Йенсена. – Научно-популярный физико-математический журнал «Квант», №4, 1990. – 95с.
3. Конюшков А. Неравенство Коши-Буняковского. – Научно-популярный физико-математический журнал «Квант», №8, 1987. – 110с.
4. Супрун В.П. Избранные задачи повышенной сложности по математике. – Мн.: Полымя, 1998. – 108 с. – («В помощь абитуриентам и студентам»)
5. Соловьев Ю.П. Неравенства (Серия: «Библиотека «Математическое просвещение»») М.: МЦНМО, 2005. — 16 с.:
6. ЕГЭ 2018, Математика, Большой сборник тематических заданий, Профильный уровень, Ященко И.В
8







 f(x) ) ) + h(x) )+ )
f(x) ) ) + h(x) )+ ) f(x) )
f(x) )  ) g(x)
) g(x) 
 ) g(x) a·f(x) a·g(x) , a
) g(x) a·f(x) a·g(x) , a  0, следовательно x2 +xy+y2 ≥ 3(x+y−1) при любых x и y. Равенство верно, когда x = y = 1.
0, следовательно x2 +xy+y2 ≥ 3(x+y−1) при любых x и y. Равенство верно, когда x = y = 1.  xy·sin𝝰
xy·sin𝝰 удовлетворяет условию задачи, следовательно указанный треугольник имеет наибольшую площадь среди всех рассматриваемых. Следовательно площадь треугольника равна 1.
удовлетворяет условию задачи, следовательно указанный треугольник имеет наибольшую площадь среди всех рассматриваемых. Следовательно площадь треугольника равна 1. ≥
≥  , при
, при  ≥ 0
≥ 0 =
=  ≥ 0
≥ 0 равны.
равны. +
+  ≤
≤  для a, b 0
для a, b 0  +
+
 ≤
≤  +
+  ≤
≤ 
 8abc
8abc  .
. +
+  +
+  ≥ 3
≥ 3 +
+  +
+ 
 +
+  +
+  ≥ 3
≥ 3 +
+  +
+  ≥ 6
≥ 6

 ,
, ,
,  ≥ 0
≥ 0 , получим:
, получим: .
. .
. .
.
 +…+
+…+ n
n +1
+1 ,
,  ,..,
,.., . В результате получим:
. В результате получим: , т.е
, т.е
 Применим неравенство между средним арифметическим и средним геометрическим для чисел 2,
Применим неравенство между средним арифметическим и средним геометрическим для чисел 2,  , т.е
, т.е
 ≥ 4abcd
≥ 4abcd ≥
≥ 
 +
+  +
+  ≥ 3
≥ 3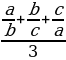 ≥ 1
≥ 1



 ≥ 2, если a + b = 2.
≥ 2, если a + b = 2. ≥ 2.
≥ 2. ≤
≤ 
 ,b =
,b =  .
.  =
= 
 +
+ ≤
≤  , откуда
, откуда  x =
x =



 + 8
+ 8 ≤
≤ 
 ≥ 1+ nx
≥ 1+ nx = (1+)
= (1+)  ≥1+(n+1)x
≥1+(n+1)x +
+  = 2
= 2 +
+  ≤ 1+
≤ 1+ 
 + 1-
+ 1-  ≥ 0, то
≥ 0, то +
+  + . . . +
+ . . . +  = 2 –
= 2 –  то неравенство
то неравенство 
 , следует, что
, следует, что  с очевидным :
с очевидным : 

 Сложив с неравенством:
Сложив с неравенством: 




 +
+ ≤
≤ 
 +
+ 2
2 ≤
≤ 
 +
+  +
+  x + y + z.
x + y + z. , z+x
, z+x  , sin2x + 1.
, sin2x + 1. , sin2x = 4sin
, sin2x = 4sin  Таким образом sin2x + 1.
Таким образом sin2x + 1. ,
,  ,
,
 +
+  │ ≤
│ ≤  ·
·  (1)
(1) ≤
≤ 
 +
+ 


 +
+  = A
= A – 2Ct + B.
– 2Ct + B. – 4 AB = 4
– 4 AB = 4  ≤ 0 , то есть
≤ 0 , то есть  : f (
: f ( +
+  + ….+
+ ….+  = 0.
= 0. =
=  =
= 

 ·
·  =
= 

 ≤
≤ 

 =55, то
=55, то  .
.
 = 1.
= 1.
 Решение:
Решение:
 =
=  = 5
= 5
 =
=  =
= 
 x
x +
+  = 1
= 1

 3.5 Неравенство Йенсена (11 класс)
3.5 Неравенство Йенсена (11 класс) +..+
+..+ ) ≤
) ≤  +…+
+…+  (1)
(1) ,
,  ,…,
,…,  € [a;b];
€ [a;b]; +…+
+…+  = 1
= 1 0
0 ≤
≤  ′ =
′ =  ·
·  ,
, ,ɤ- углы треугольника.
,ɤ- углы треугольника. ≥
≥  ))
)) ln sin
ln sin  sin
sin  sin
sin 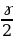
 = 3
= 3
 . И оказывается , что доказательство этой последовательности равносильно доказательству всего двух таких утверждений:
. И оказывается , что доказательство этой последовательности равносильно доказательству всего двух таких утверждений: .
. следует
следует 
 , при l ≤ k , то верно
, при l ≤ k , то верно 
 , n= 1,2,3…
, n= 1,2,3… = 32
= 32  = 25
= 25





 – 2.
– 2. +
+ 

 ) ≥
) ≥  – верно.
– верно. (
( ) ≥
) ≥ 
 ) ≥
) ≥ 
 +a
+a +
+ +
+  ·
· +
+  (a-b) +
(a-b) +  ).
). , значит (a-b)
, значит (a-b) , значит (a-b)
, значит (a-b) MPN 60◦. Так же , что в P прилетели из
MPN 60◦. Так же , что в P прилетели из  ,….
,….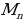 . Отсюда , что из углов
. Отсюда , что из углов  P
P не
не  .
. 


 3.
3. x+
x+ x = 1
x = 1 x
x x
x
 cos x = 0 или cos x =1, k€Z x=
cos x = 0 или cos x =1, k€Z x= +2π , k€
+2π , k€ Задача1.
Задача1. +
+  =
=  +
+ 
 ·
· · 4 ≥
· 4 ≥ 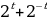 =
=  = 4
= 4 = 0
= 0 +
+ 
 = 2
= 2
 +
+  = 2.
= 2. + 5
+ 5 +
+  +
+  ≥ 0
≥ 0 +
+  = │x - 2│ + │x - 4│
= │x - 2│ + │x - 4│ +
+  = 2 (*)
= 2 (*)
















