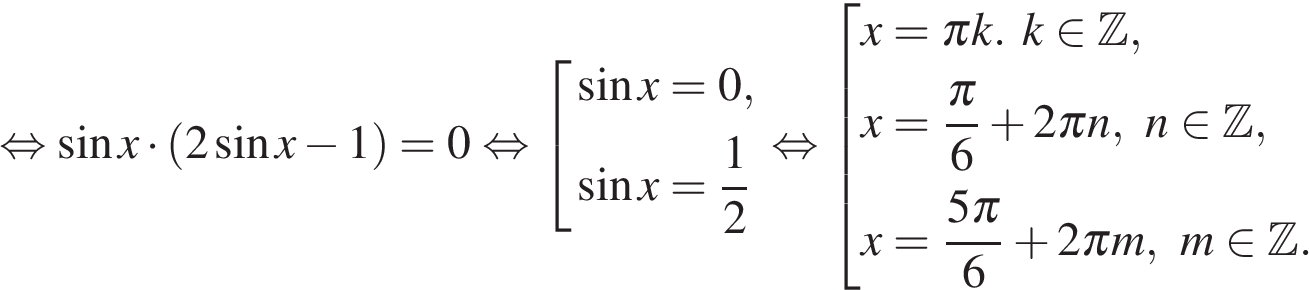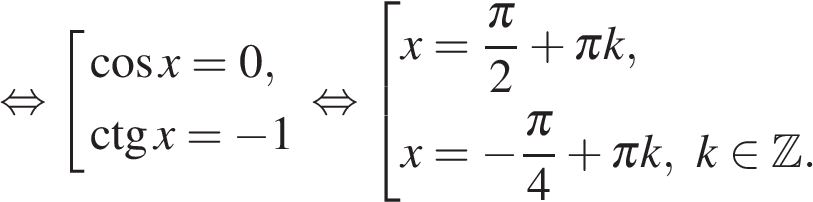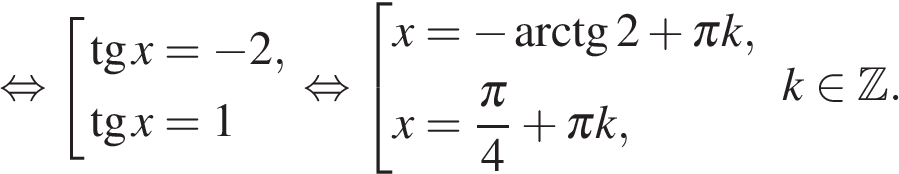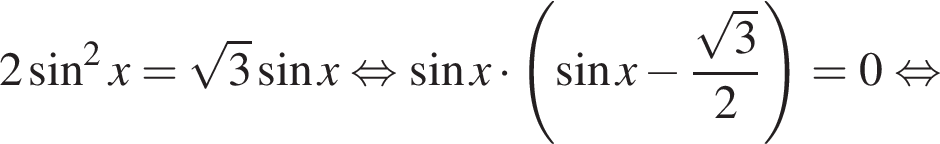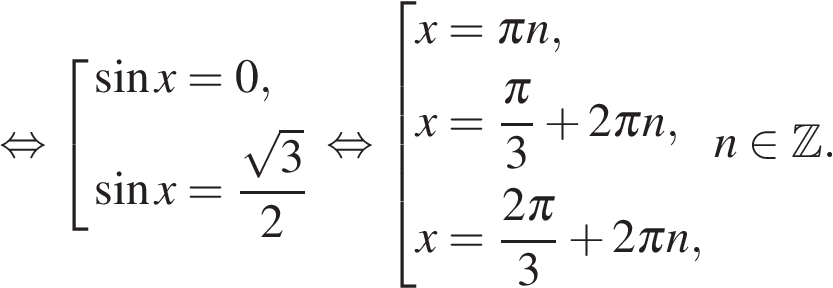Тригонометрические уравнения, разложение на множители
1. Задание 13 № 507886
а) Решите уравнение 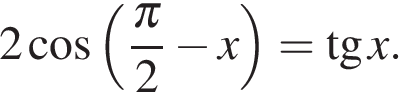
б) Укажите корни этого уравнения, принадлежащие отрезку 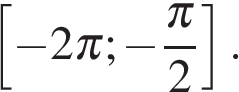
Решение.
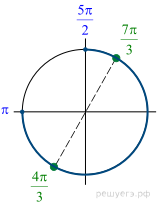
а) Преобразуем уравнение:

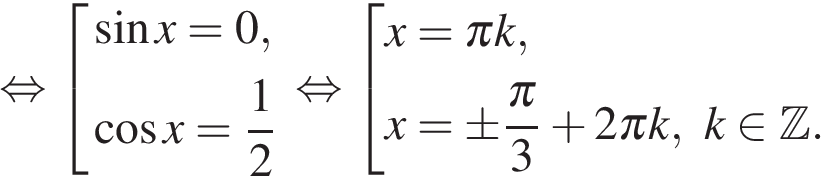
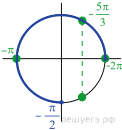
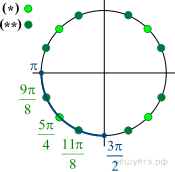
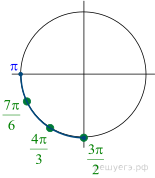
б) Отберем корни на промежутке  с помощью тригонометрической окружности. Получаем
с помощью тригонометрической окружности. Получаем 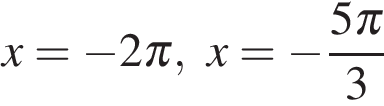 и
и 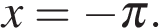
Ответ: а) 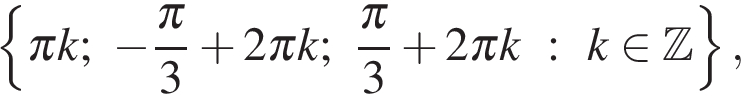 б)
б) 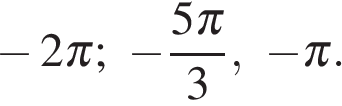
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
507886
а) 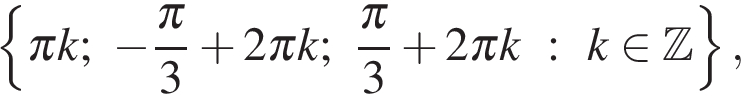 б)
б) 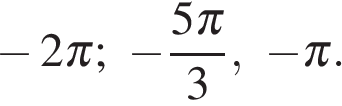
Раздел кодификатора ФИПИ/Решу ЕГЭ: Уравнения, рациональные относительно тригонометрических функций
Методы алгебры: Формулы приведения
2. Задание 13 № 500111
а) Решите уравнение 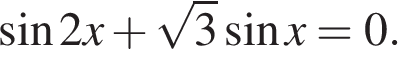
б) Найдите все корни этого уравнения, принадлежащие отрезку 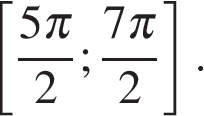
Решение.
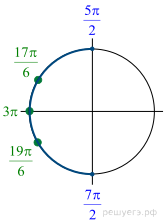 а) Запишем уравнение в виде
а) Запишем уравнение в виде
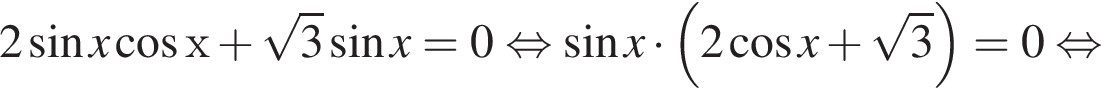
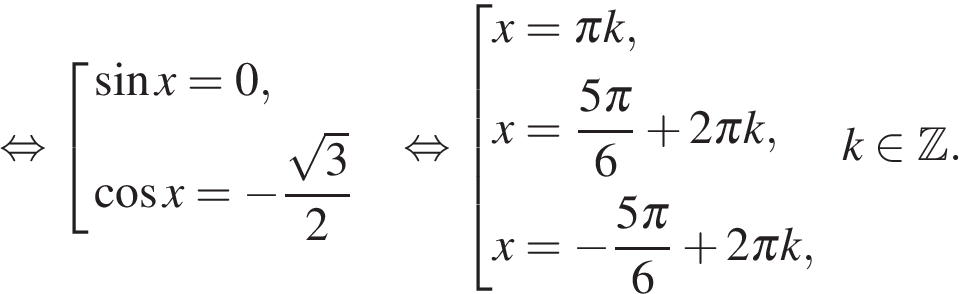
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 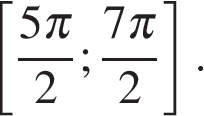 Получим числа:
Получим числа: 
Ответ: а) 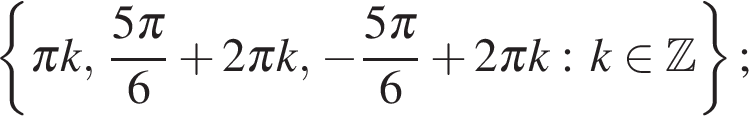 б)
б) 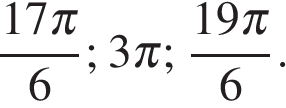
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
500111
а) 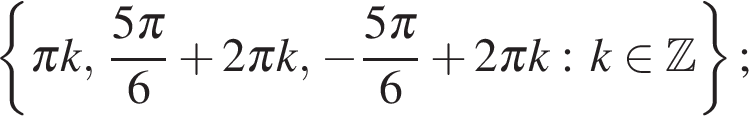 б)
б) 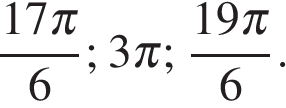
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла
3. Задание 13 № 509201
а) Решите уравнение 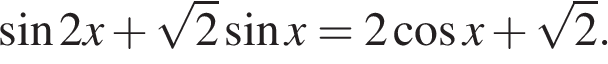
б) Укажите корни этого уравнения, принадлежащие отрезку 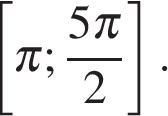
Решение.

а) Используем формулу синуса двойного угла, выносим за скобки:

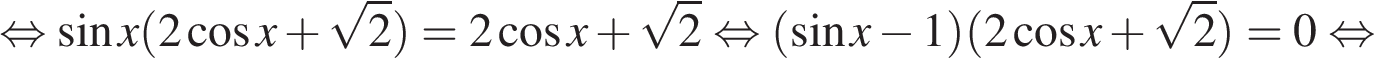
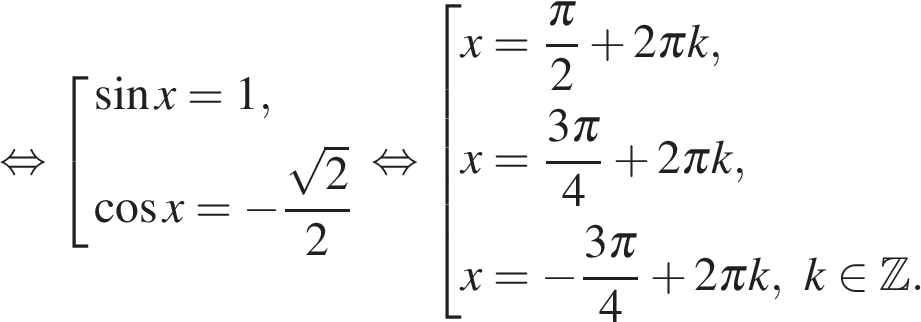
б) Изображая корни на единичной окружности, находим, что отрезку 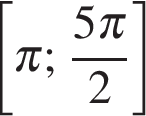 принадлежат корни
принадлежат корни 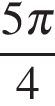 и
и 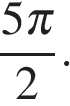
Ответ:а) 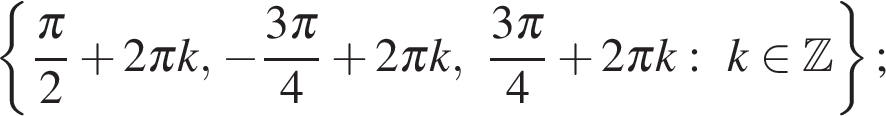 б)
б) 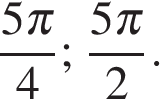
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
509201
а) 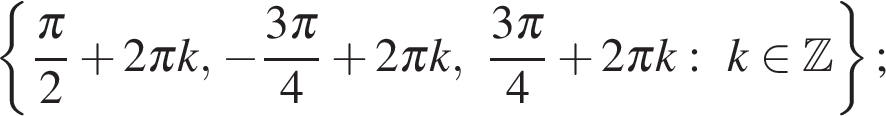 б)
б) 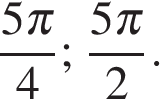
Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
4. Задание 13 № 507638
а) Решите уравнение 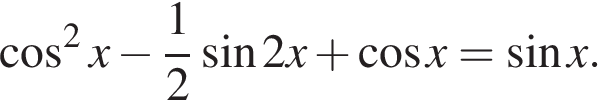
б) Найдите все корни этого уравнения, принадлежащие промежутку 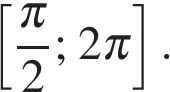
Решение.
 а) Перенесём все члены в левую часть, преобразуем и разложим левую часть на множители:
а) Перенесём все члены в левую часть, преобразуем и разложим левую часть на множители:
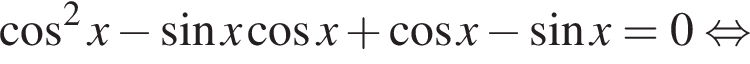
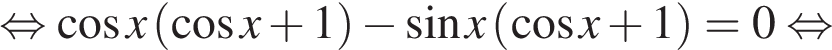

1 случай. Если 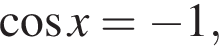 то
то 
2 случай. Если 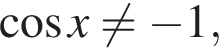 то
то  При
При 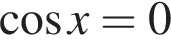 решений нет. Разделим обе части уравнения на
решений нет. Разделим обе части уравнения на 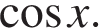 Получаем
Получаем 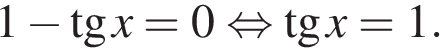
Тогда 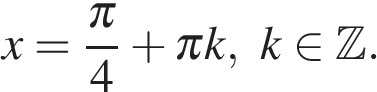
б) Отрезку 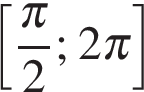 принадлежат корни
принадлежат корни 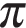 и
и 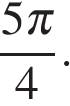
Ответ: а) 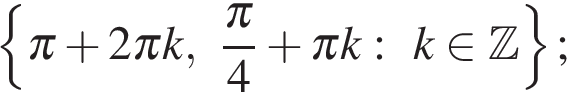 б)
б) 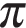 и
и 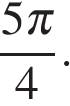
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
507638
а) 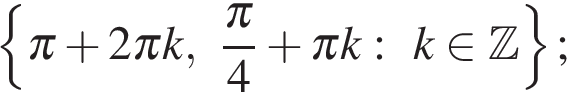 б)
б) 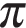 и
и 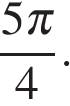
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка, Формулы двойного угла
5. Задание 13 № 485932
Дано уравнение 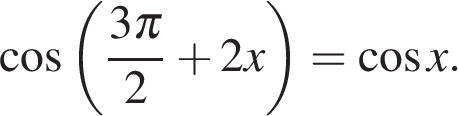
а) Решите уравнение;
б) Укажите корни уравнения, принадлежащие отрезку 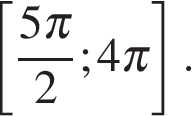
Решение.
Используем формулу приведения и синуса двойного угла:
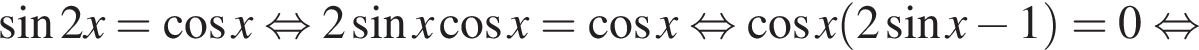
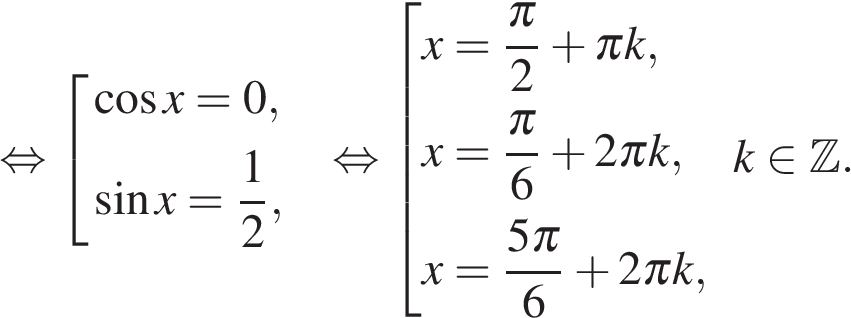

б) С помощью единичной окружности отберём корни на отрезке 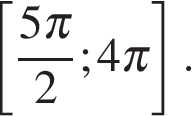 Находим:
Находим: 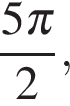
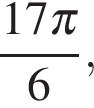

Ответ: а) 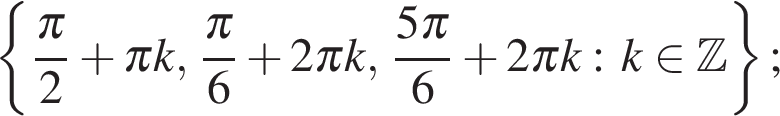 б)
б) 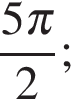
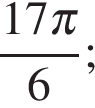

Примечание.
Уравнение может быть так же решено при помощи следующей теоремы:

Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
485932
а) 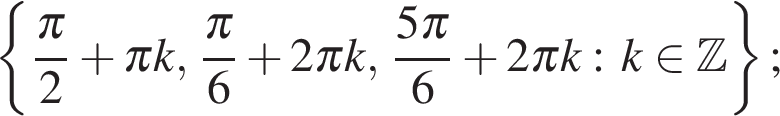 б)
б) 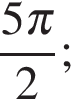
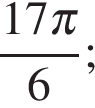

Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла, Формулы приведения
6. Задание 13 № 500961
а) Решите уравнение 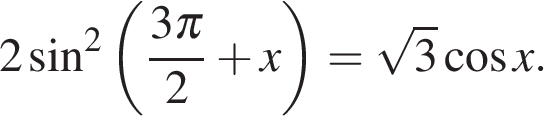
б) Найдите все корни этого уравнения, принадлежащие промежутку 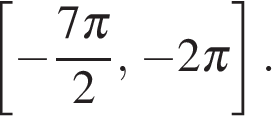
Решение.
 а) Заметим, что
а) Заметим, что 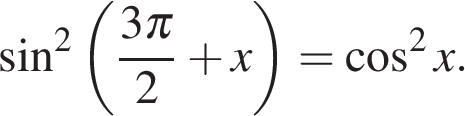 Поэтому уравнение можно переписать в виде
Поэтому уравнение можно переписать в виде 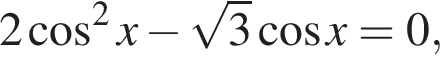 откуда
откуда 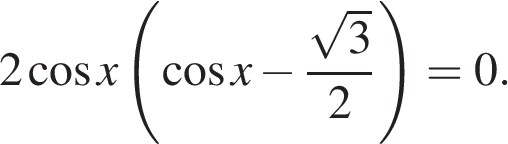 Значит, либо
Значит, либо 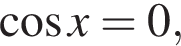 откуда
откуда 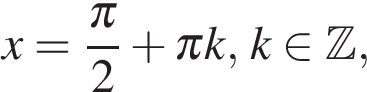 либо
либо 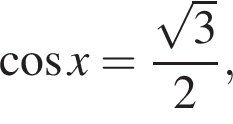 откуда
откуда 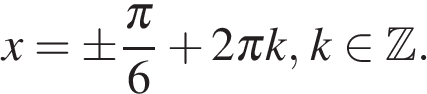
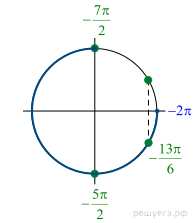
б) Отберем с помощью единичной окружности корни уравнения, принадлежащие промежутку 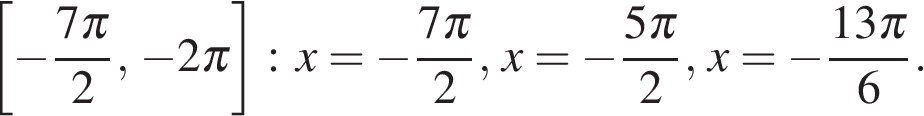
Ответ: а) 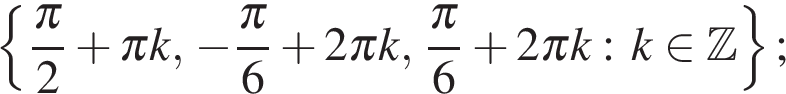 б)
б) 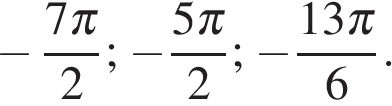
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
500961
а) 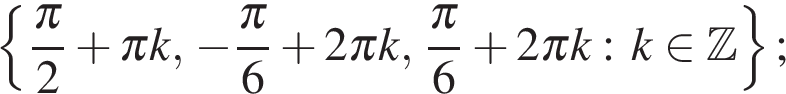 б)
б) 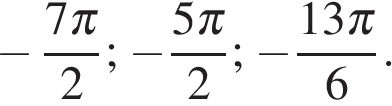
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
7. Задание 13 № 526590
а) Решите уравнение 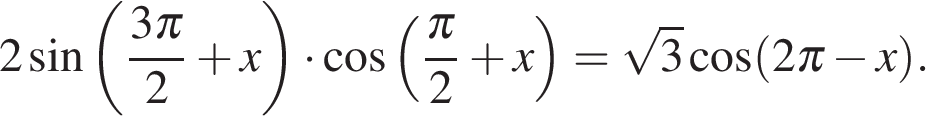
б) Найдите все корни этого уравнения, принадлежащие отрезку 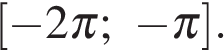
Решение.
а) Преобразуем уравнение:
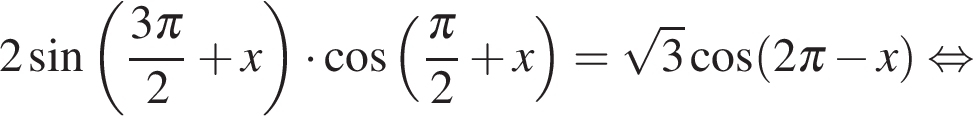
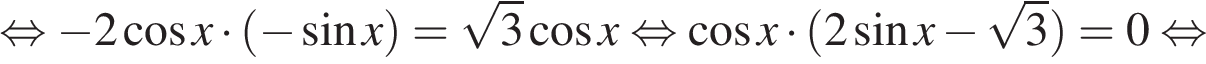
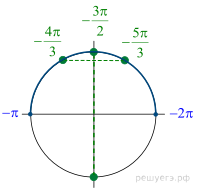
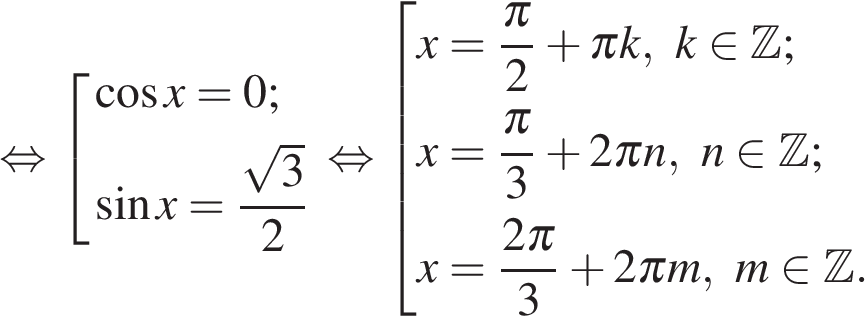
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 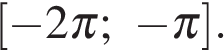 Получим числа
Получим числа 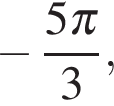
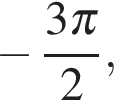
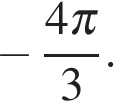
Ответ: а) 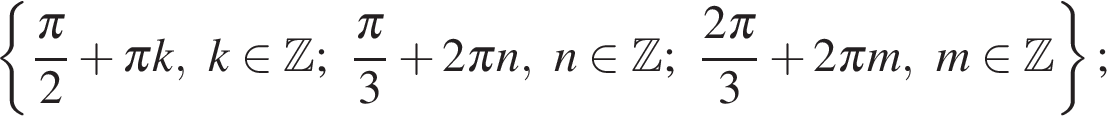 б)
б) 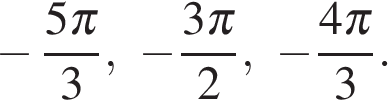
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
526590
а) 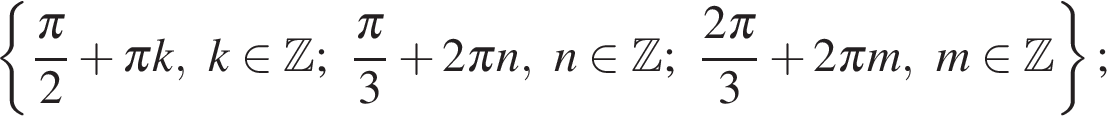 б)
б) 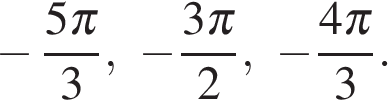
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
8. Задание 13 № 500346
а) Решите уравнение 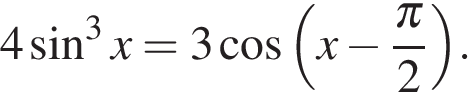
б) Найдите все корни этого уравнения, принадлежащие отрезку 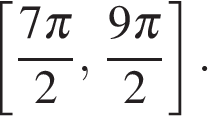
Решение.
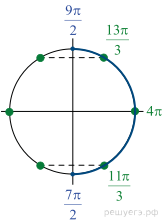 а) Запишем уравнение в виде
а) Запишем уравнение в виде 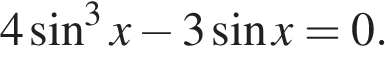
Значит, или 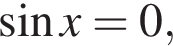 откуда
откуда 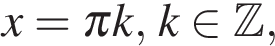 или
или 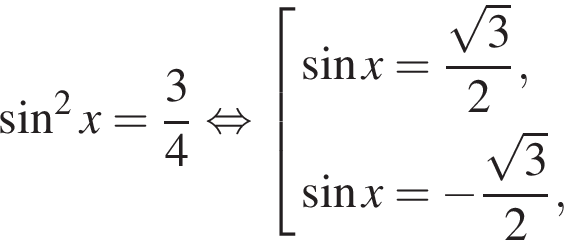 откуда
откуда 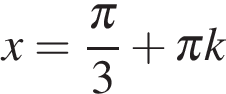 или
или 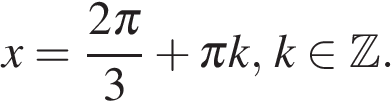
б) С помощью числовой окружности отберем корни, принадлежащие отрезку 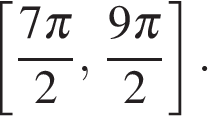 Получим числа:
Получим числа: 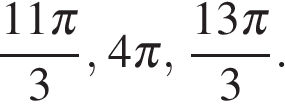
Ответ: а) 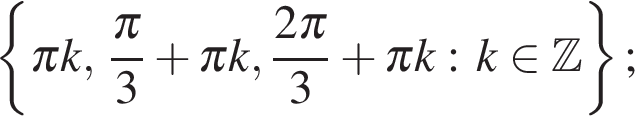 б)
б) 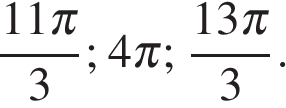
Примечание.
Внимательный читатель, конечно, узнал формулу синуса тройного угла:
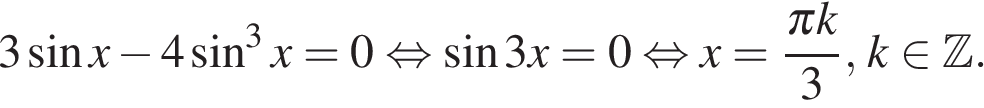
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
500346
а) 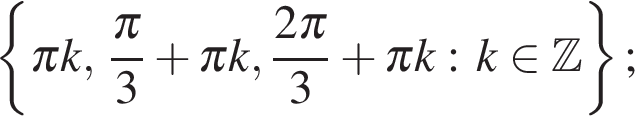 б)
б) 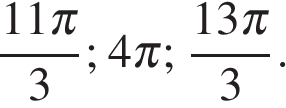
Примечание.
Внимательный читатель, конечно, узнал формулу синуса тройного угла:
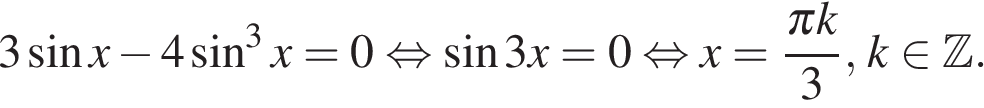
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
9. Задание 13 № 501507
а) Решите уравнение 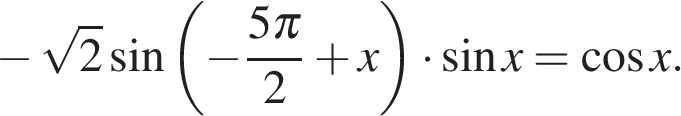
б) Найдите все корни этого уравнения, принадлежащие отрезку 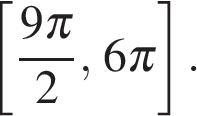
Решение.
а) В силу нечетности и периодичности синуса имеем:
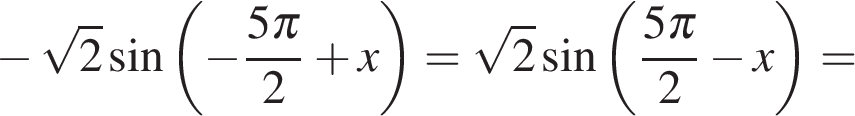
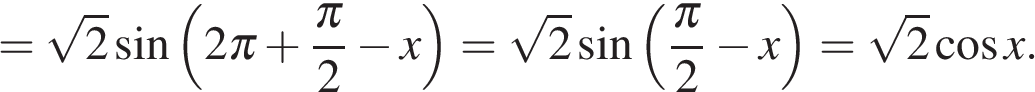
Далее имеем:
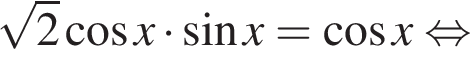
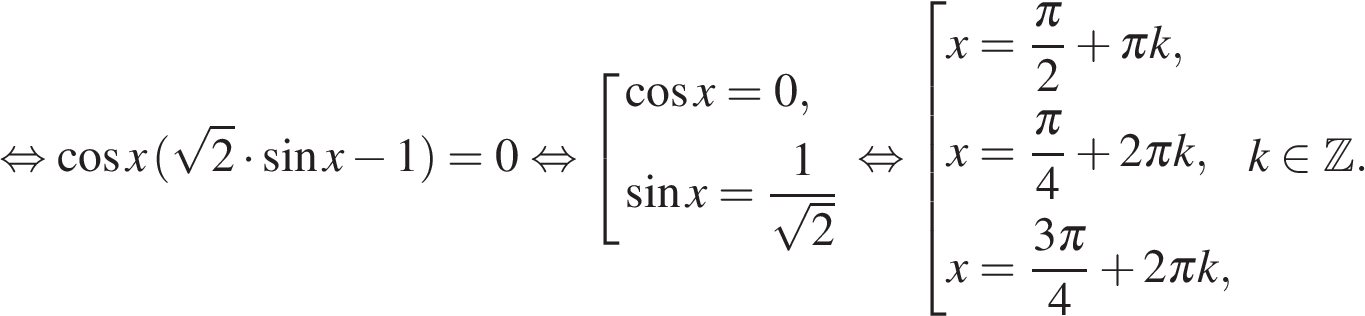
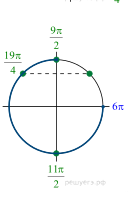
б) При помощи числовой прямой или тригонометрической окружности (см. рис.) для каждой из задающих решения серий отберем корни уравнения, принадлежащие отрезку 
Находим три решения: 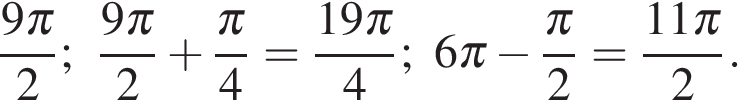
Ответ:
а) 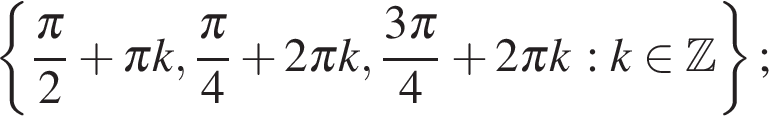
б) 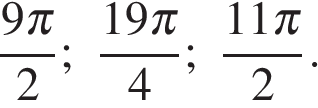
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
501507
а) 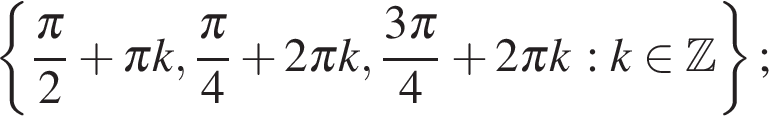
б) 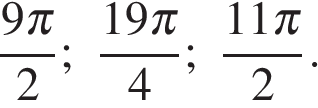
Источник: ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 1., ЕГЭ по математике 23.04.2013. Досрочная волна. Запад. Вариант 1., Задания 13 (С1) ЕГЭ 2013
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
10. Задание 13 № 513071
а) Решите уравнение 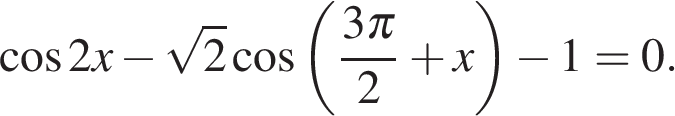
б) Укажите корни этого уравнения, принадлежащие отрезку 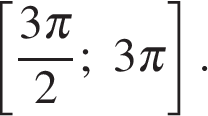
Решение.
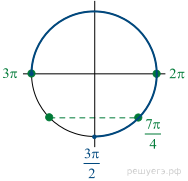
Имеем:
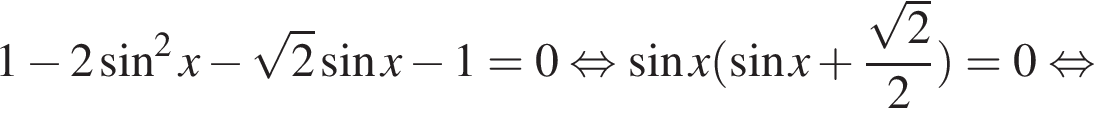
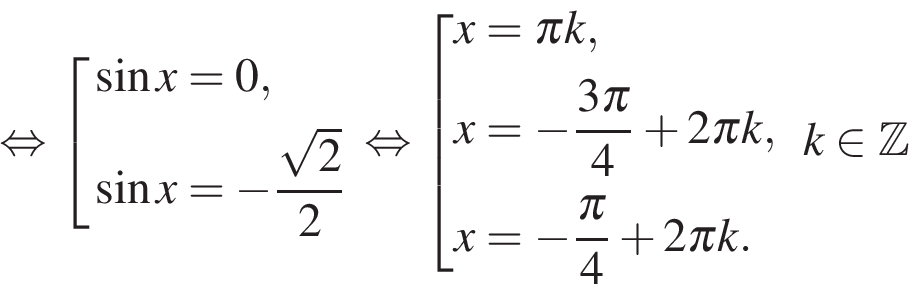
б) На указанном промежутке лежат точки 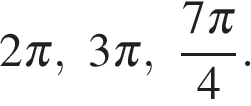
Ответ: а) 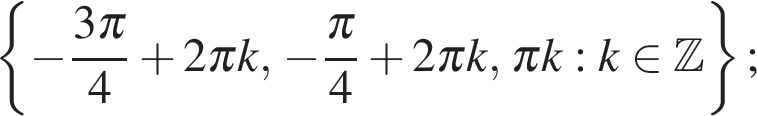 б)
б) 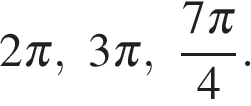
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
513071
а) 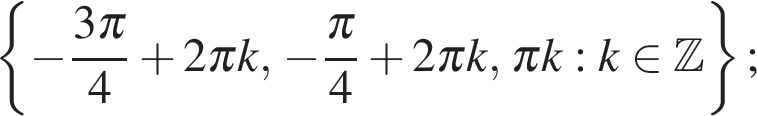 б)
б) 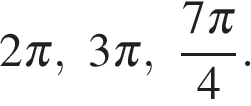
Источник: Материалы для экспертов ЕГЭ 2016
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла, Формулы приведения
11. Задание 13 № 500815
а) Решите уравнение 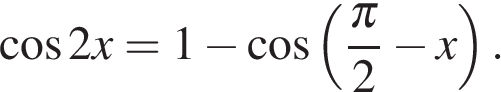
б) Найдите все корни этого уравнения, принадлежащие промежутку 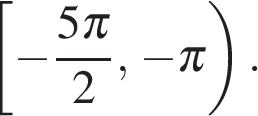
Решение.
а) Так как 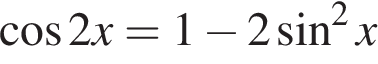 и
и 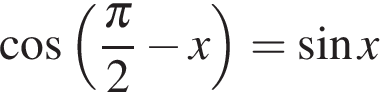 , имеем:
, имеем:
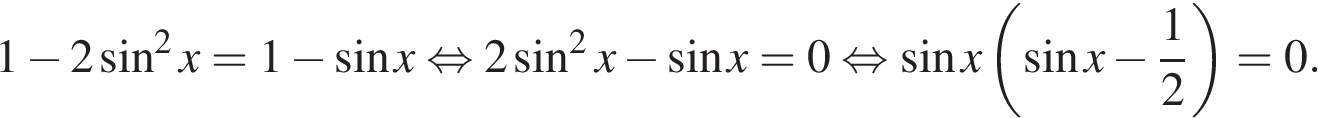
Корни уравнения: 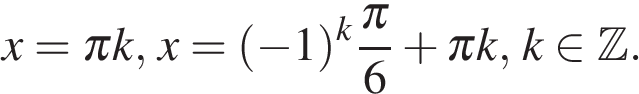
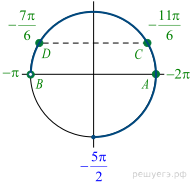
б) Корни уравнения  изображаются точками
изображаются точками 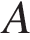 и
и 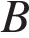 , а корни уравнения
, а корни уравнения 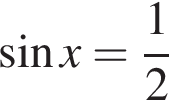 — точками
— точками 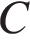 и
и 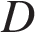 , промежуток
, промежуток  изображается жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения:
изображается жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения: 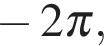
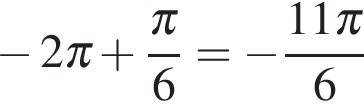 и
и 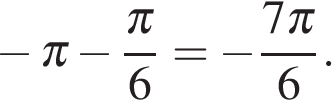
Ответ:а) 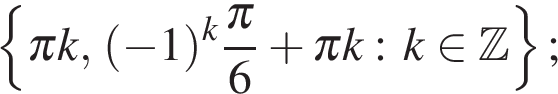 б)
б) 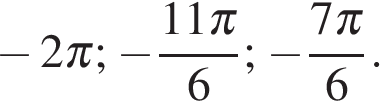
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
500815
а) 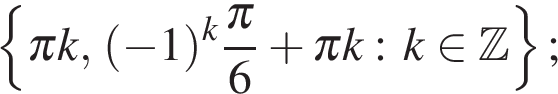 б)
б) 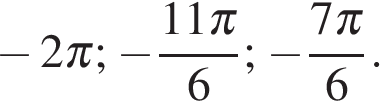
Источник: Демонстрационная версия ЕГЭ—2013 по математике.
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла, Формулы приведения
12. Задание 13 № 520495
а) Решите уравнение 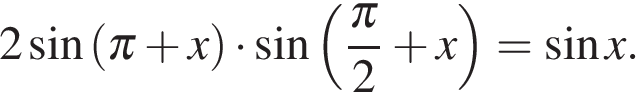
б) Найдите все корни этого уравнения, принадлежащие отрезку 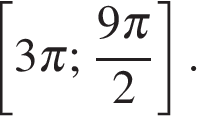
Решение.
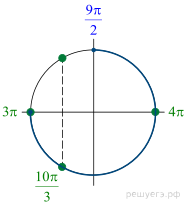 а) Преобразуем уравнение :
а) Преобразуем уравнение :  Получаем
Получаем 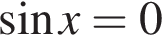 или
или 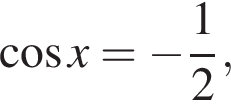 откуда
откуда 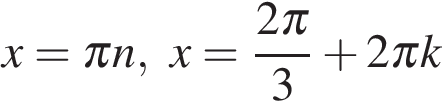 или
или 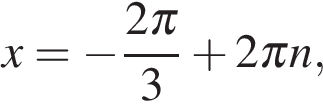 где
где 
б) На отрезке 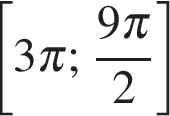 корни отберем с помощью единичной окружности. Получаем
корни отберем с помощью единичной окружности. Получаем 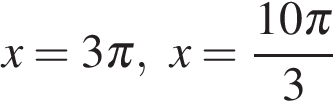 и
и 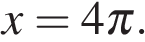
Ответ: а) 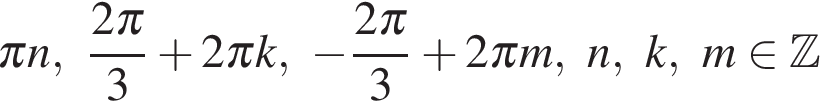 б)
б) 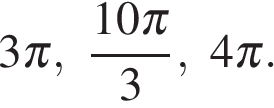
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
520495
а) 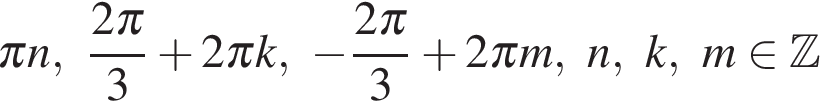 б)
б) 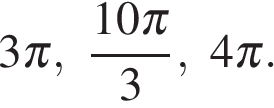
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы приведения
13. Задание 13 № 517262
а) Решите уравнение 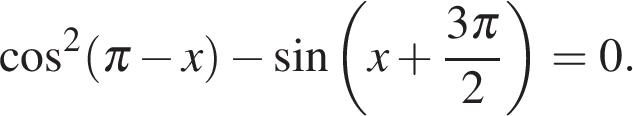
б) Укажите корни этого уравнения, принадлежащие отрезку 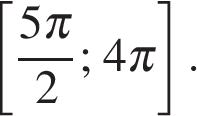
Решение.
 а) Используя формулы приведения, получим уравнение, квадратное относительно косинуса:
а) Используя формулы приведения, получим уравнение, квадратное относительно косинуса:
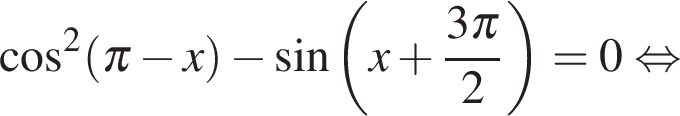
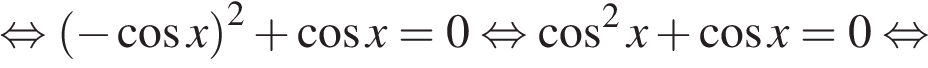
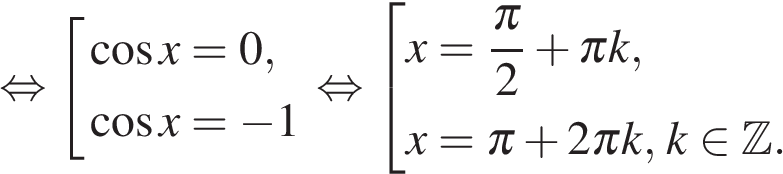
б) Отрезку 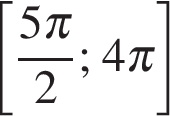 принадлежат корни
принадлежат корни 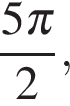
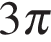 и
и 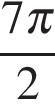 (см. рис.).
(см. рис.).
Ответ: а) 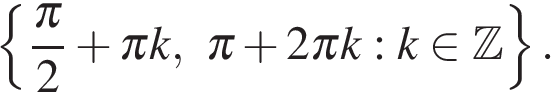 б)
б) 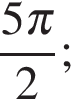

Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
517262
а) 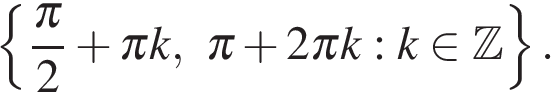 б)
б) 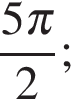
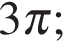

Источник: ЕГЭ по математике — 2017. Досрочная волна, резервный день, вариант А. Ларина (часть С).
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы приведения, периодичность тригонометрических функций
14. Задание 13 № 509888
а) Решите уравнение 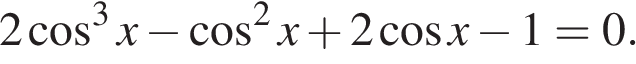
б) Укажите корни этого уравнения, принадлежащие отрезку 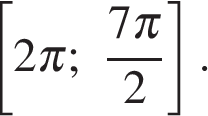
Решение.
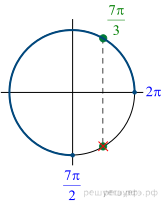 Решим уравнение:
Решим уравнение:

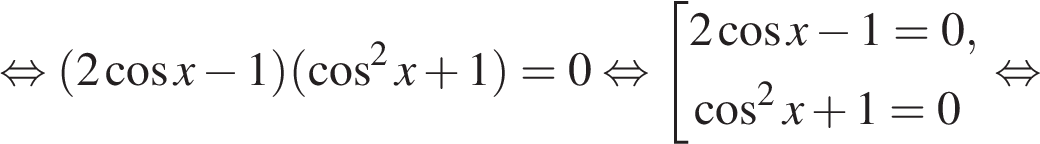
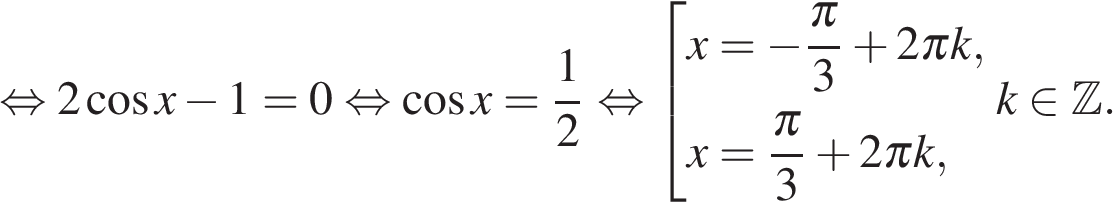
б) Укажем корни этого уравнения, принадлежащие отрезку 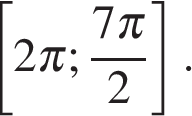 Получим точку
Получим точку 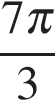 .
.
Ответ: а) 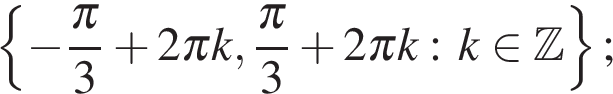 б)
б) 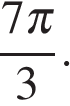
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
509888
а) 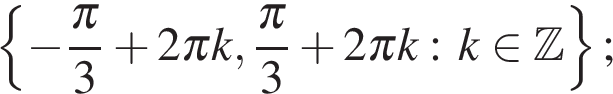 б)
б) 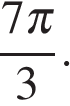
Источник: ЕГЭ по математике 26.03.2015. Досрочная волна, Восток.
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
15. Задание 13 № 485977
а) Решите уравнение 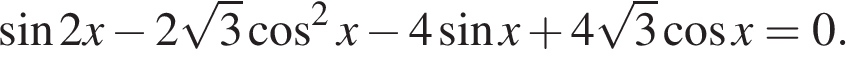
б) Найдите все корни этого уравнения, принадлежащие промежутку 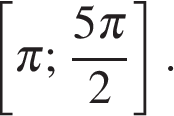
Решение.
 а) Разложим левую часть на множители:
а) Разложим левую часть на множители:
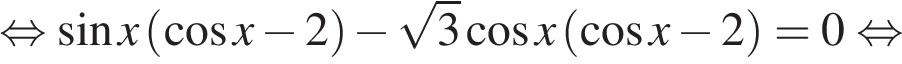
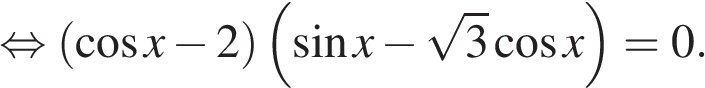
Уравнение 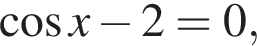 не имеет корней. Имеем
не имеет корней. Имеем 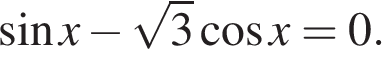
Если 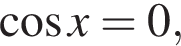 то
то 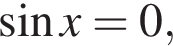 это невозможно. Это однородное уравнение первой степени, разделим обе его части на
это невозможно. Это однородное уравнение первой степени, разделим обе его части на 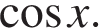 Получаем:
Получаем:
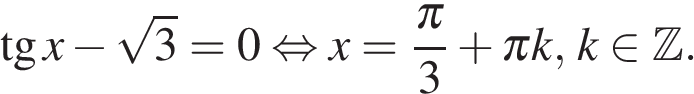
б) Отрезку 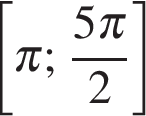 принадлежат корни
принадлежат корни 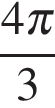 и
и 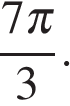 (см. рис.)
(см. рис.)
Ответ: а) 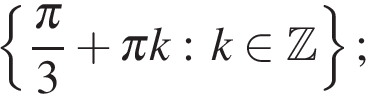 б)
б) 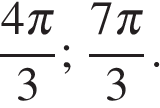
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Раздел кодификатора ФИПИ/Решу ЕГЭ: Однородные тригонометрические уравнения, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы двойного угла
16. Задание 13 № 501486
а) Решите уравнение: 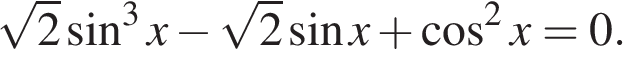
б) Найдите все корни этого уравнения, принадлежащие отрезку 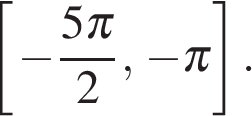
Решение.
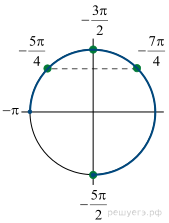 а) Запишем уравнение в виде:
а) Запишем уравнение в виде:
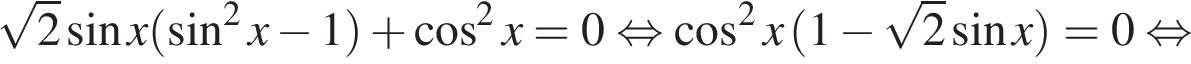
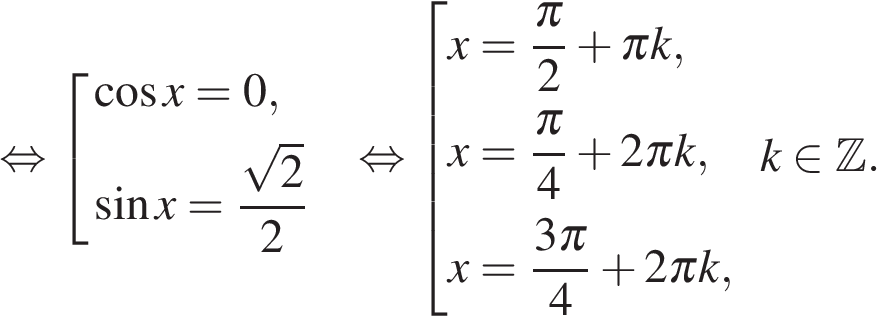
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 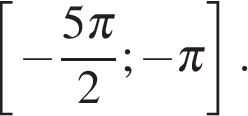 Получим числа
Получим числа 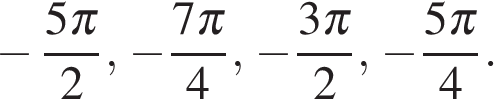
Замечание. Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т.п.
Ответ: а) 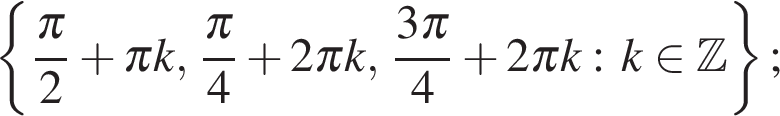 б)
б) 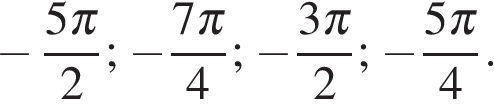
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
501486
а) 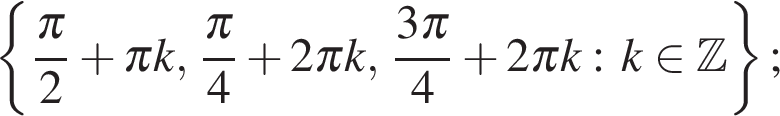 б)
б) 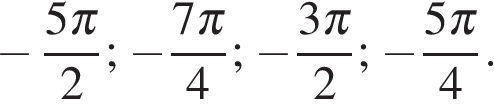
Раздел кодификатора ФИПИ/Решу ЕГЭ: Основное тригонометрическое тождество и его следствия, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
17. Задание 13 № 520973
а) Решите уравнение 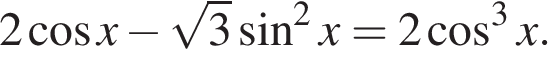
б) Определите, какие из его корней принадлежат отрезку 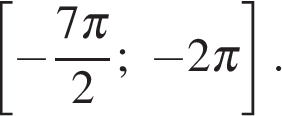
Решение.
 а) Запишем исходное уравнение в виде:
а) Запишем исходное уравнение в виде:
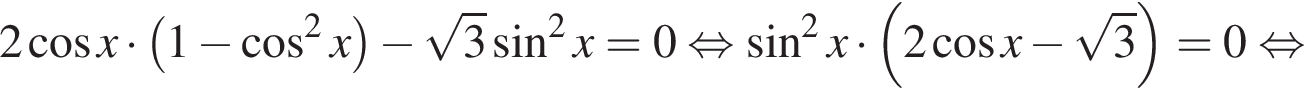
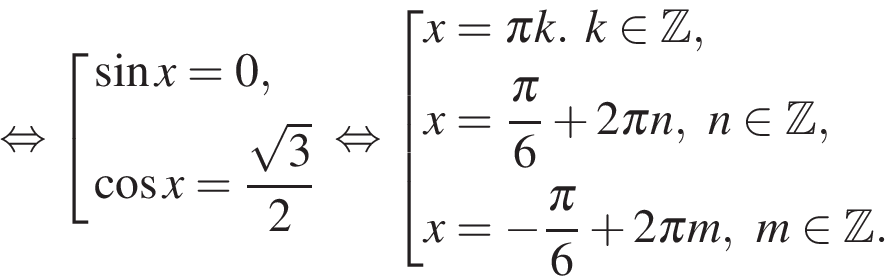
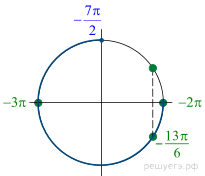
б) С помощью числовой окружности отберем корни, принадлежащие отрезку 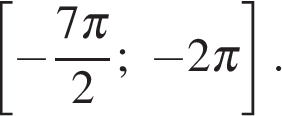 Получим числа:
Получим числа: 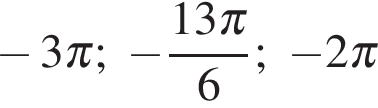 .
.
Ответ: а) 

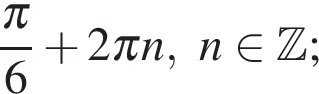
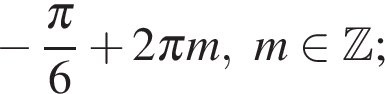 б)
б) 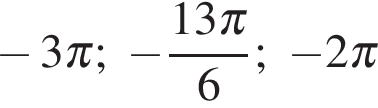 .
.
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
520973
а) 

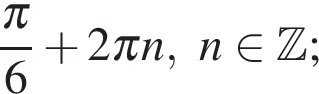
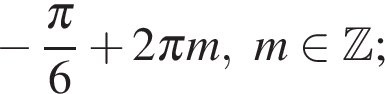 б)
б) 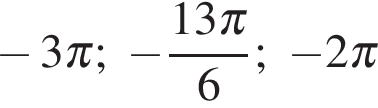 .
.
Источник: ЕГЭ — 2018. Основная волна, резервный день 25.06.2018. Вариант 501 (C часть)., Задания 13 (С1) ЕГЭ 2018
Раздел кодификатора ФИПИ/Решу ЕГЭ: Основное тригонометрическое тождество и его следствия, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
18. Задание 13 № 517829
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 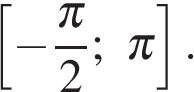
Решение.
а) Имеем:

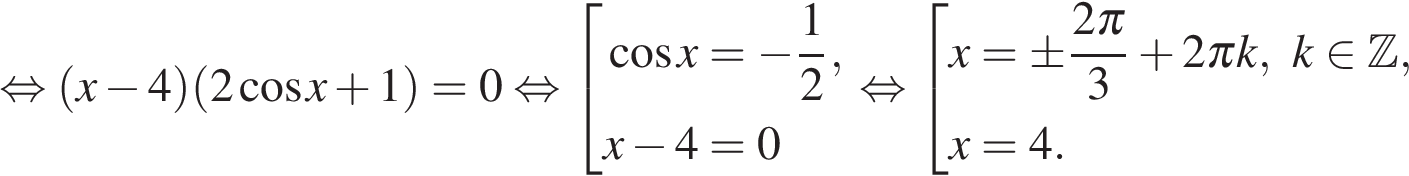
б) 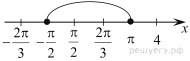 При помощи числовой оси отберем корни, принадлежащие отрезку
При помощи числовой оси отберем корни, принадлежащие отрезку 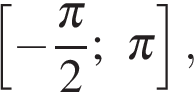 получим число
получим число 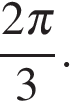
Ответ: а) 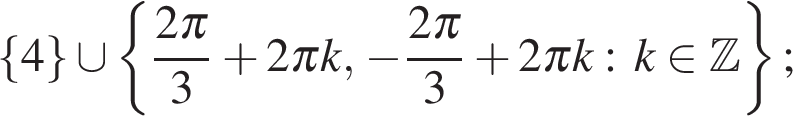 б)
б) 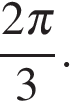
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
517829
а) 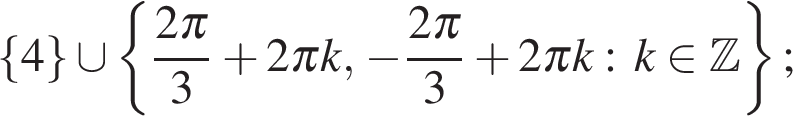 б)
б) 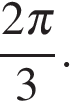
Источник: ЕГЭ — 2017. Резервный день 28.06.2017. Восток (C часть).
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
19. Задание 13 № 485973
а) Решите уравнение 
б) Укажите корни уравнения, принадлежащие отрезку 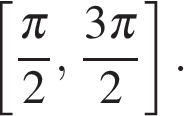
Решение.
а) Преобразуем уравнение:
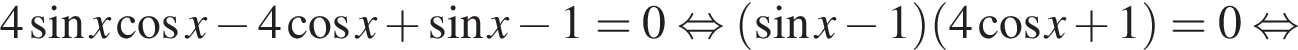
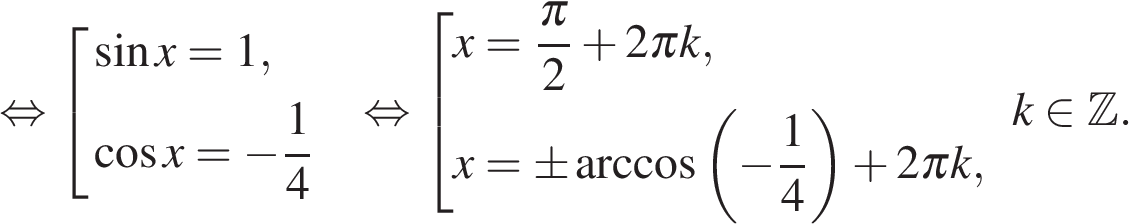
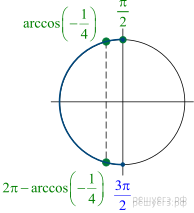
б) С помощью числовой окружности отберем корни на отрезке 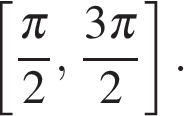 Получим числа:
Получим числа: 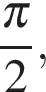


Ответ: а) 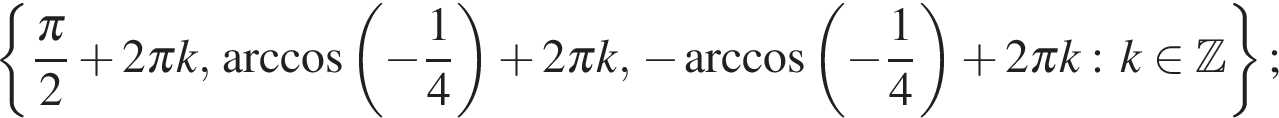 б)
б) 
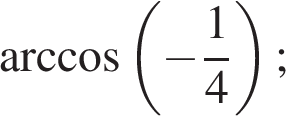

Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
485973
а) 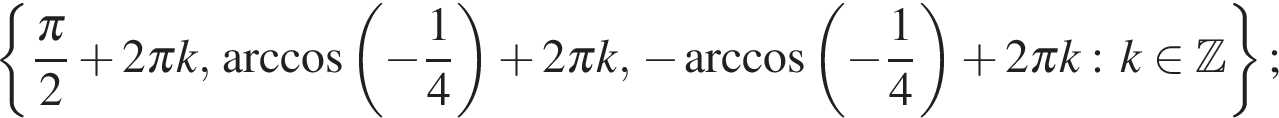 б)
б) 
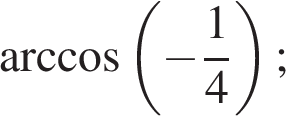

Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка, Формулы двойного угла
20. Задание 13 № 505308
а) Решите уравнение 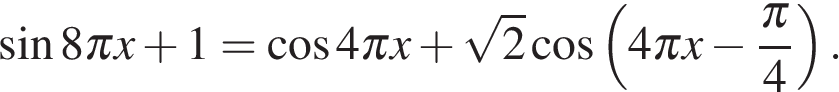
б) Найдите все корни этого уравнения, принадлежащие отрезку 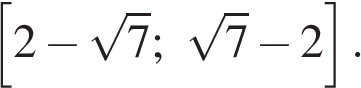
Решение.
а) Преобразуем уравнение:
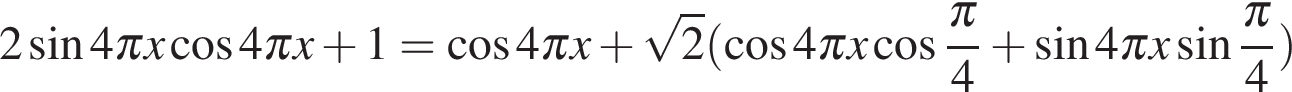
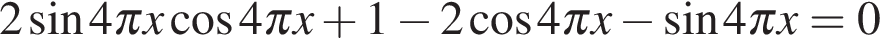
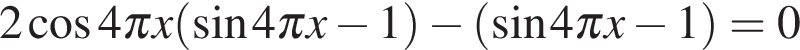

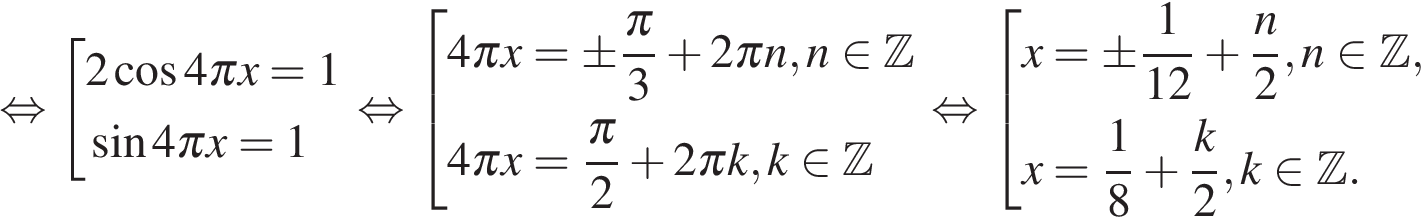
б) Ограничим каждое полученное решение из пункта «а» и решим эти неравенства:
1)
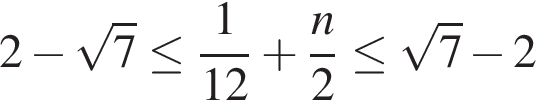
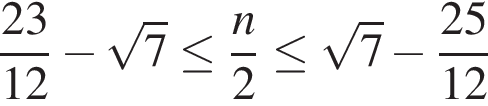
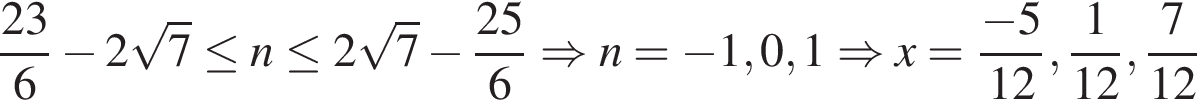
2)
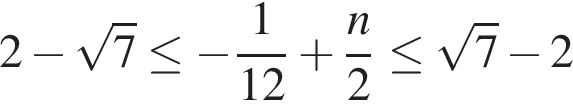
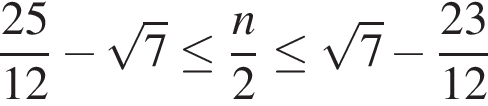
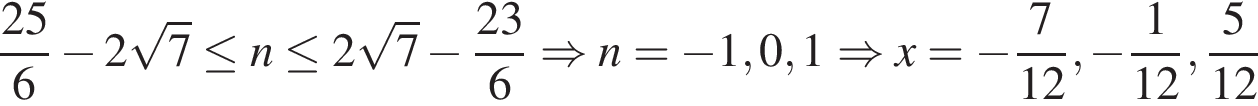
3)
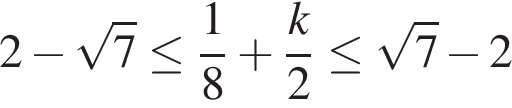
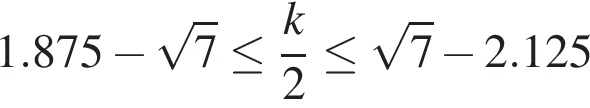
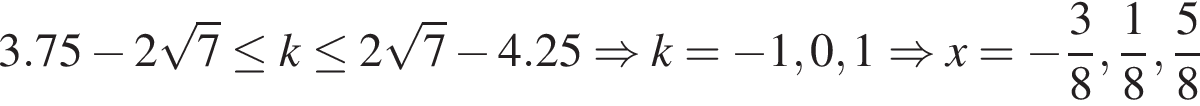
Ответ: а) 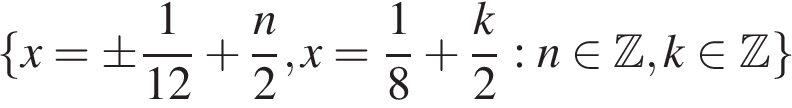 , б)
, б) 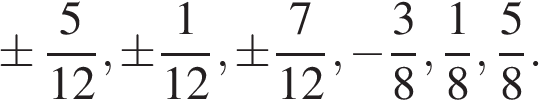
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
505308
а) 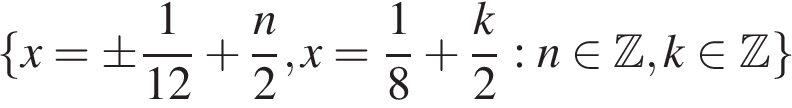 , б)
, б) 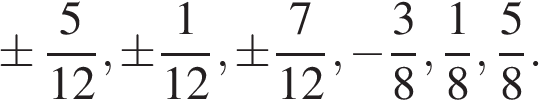
Раздел: Алгебра
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка, Тригонометрические формулы суммы и разности аргументов, Формулы двойного угла
21. Задание 13 № 507583
а) Решите уравнение: 
б) Найдите все корни этого уравнения, принадлежащие отрезку 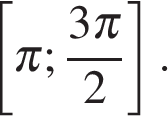
Решение.
а) Воспользуемся формулой 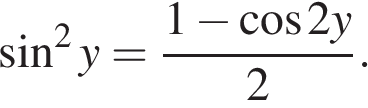 Из неё следует, что
Из неё следует, что 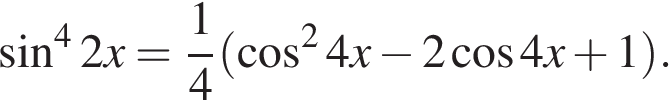 Поэтому уравнение можно преобразовать так:
Поэтому уравнение можно преобразовать так:
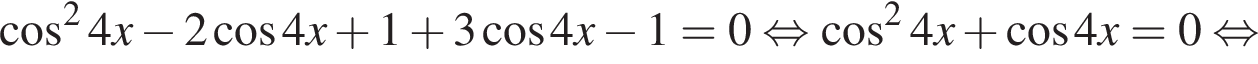
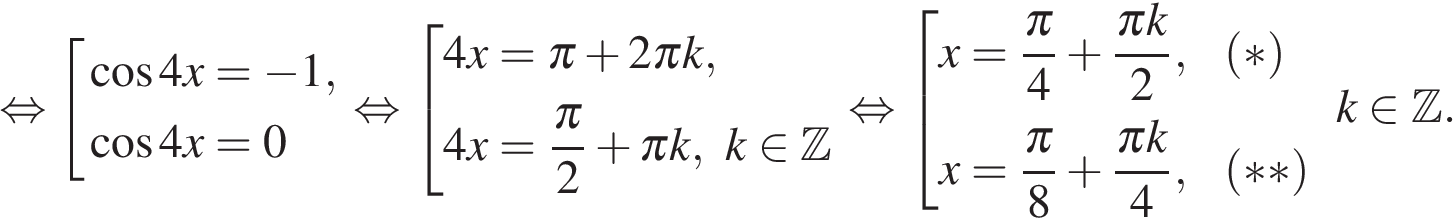
б) При помощи тригонометрической окружности отберём корни, принадлежащие заданному отрезку.
Получим: 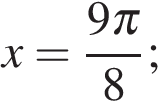
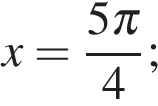

Ответ: а) 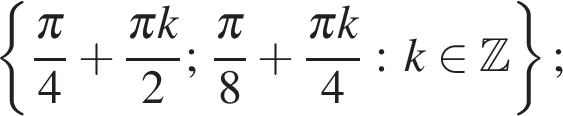 б)
б) 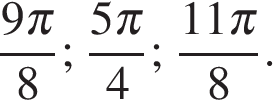
Приведём другое решение пункта а.
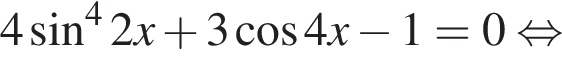

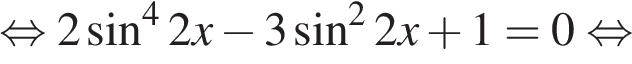
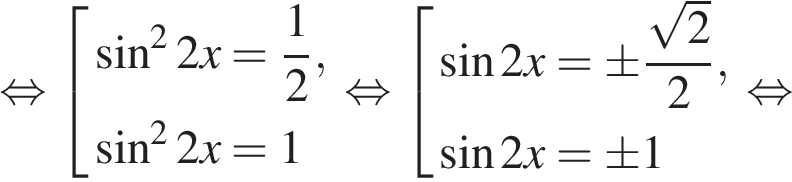
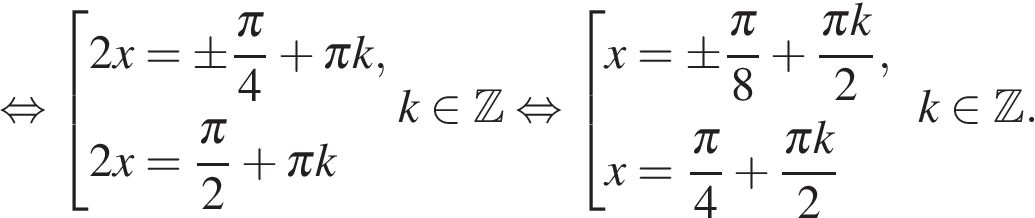
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
507583
а) 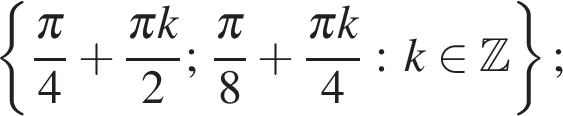 б)
б) 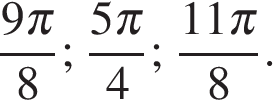
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Формулы половинного аргумента
22. Задание 13 № 520783
а) Решите уравнение: 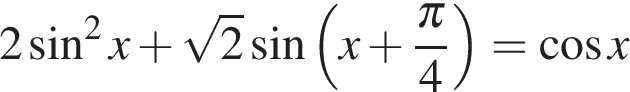 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку 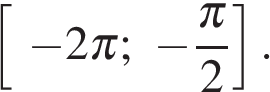
Решение.
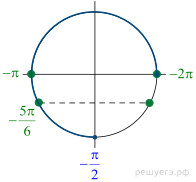
а) Выполним преобразования:
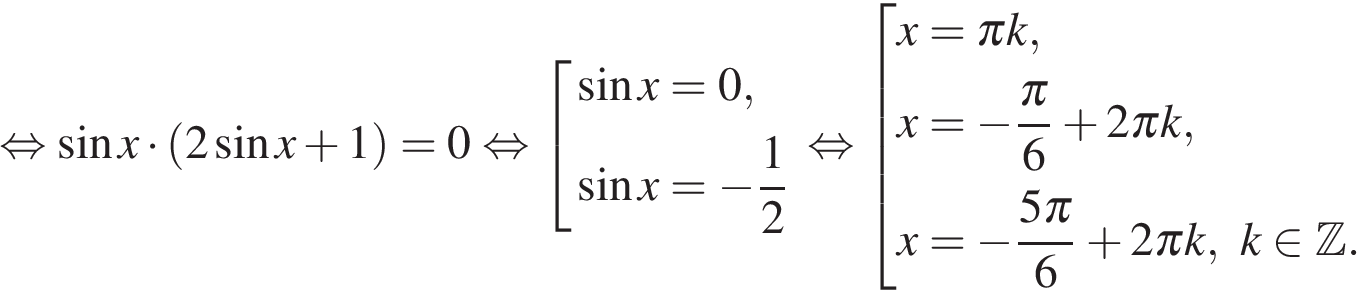
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 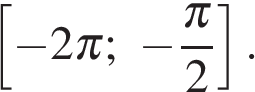
Получим числа: 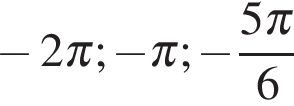 .
.
Ответ: а) 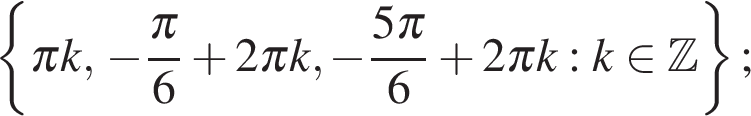 б)
б) 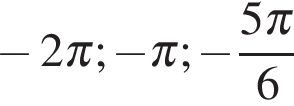
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
520783
а) 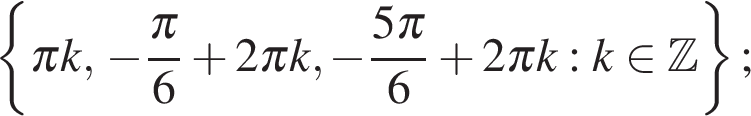 б)
б) 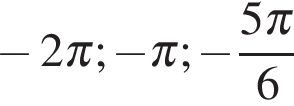
Источник: ЕГЭ — 2018. Основная волна 01.06.2018. Вариант 401 (C часть)., Задания 13 (С1) ЕГЭ 2018
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители, Тригонометрические формулы суммы или разности аргументов
23. Задание 13 № 520802
а) Решите уравнение: 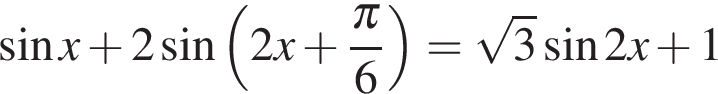
б) Определите, какие из его корней принадлежат отрезку 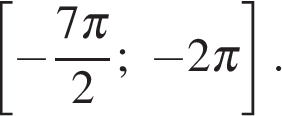
Решение.

а) Выполним преобразования:
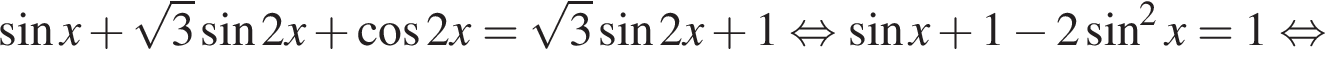
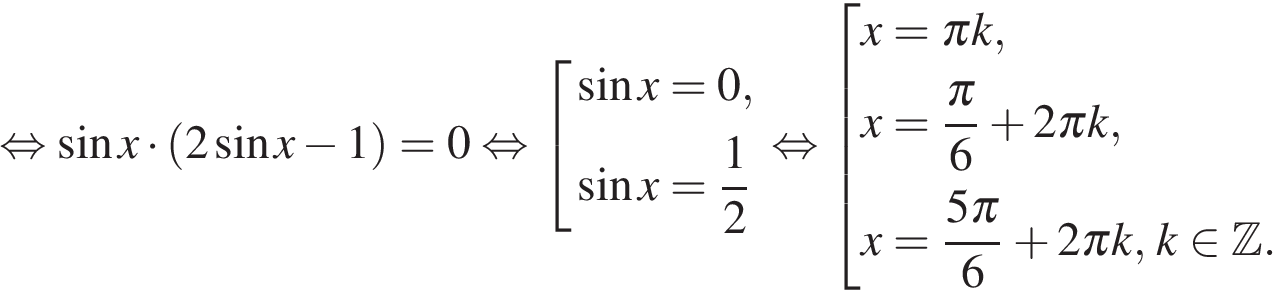
б) С помощью числовой окружности отберем корни, принадлежащие
отрезку 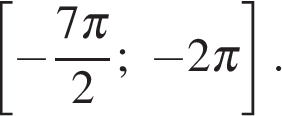 Получим числа:
Получим числа: 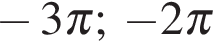 и
и 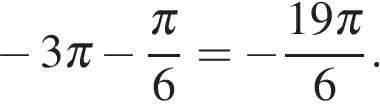
Ответ: а) 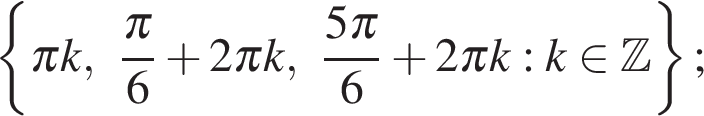 б)
б) 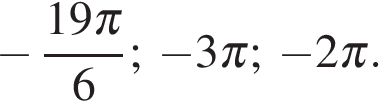
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
520802
а) 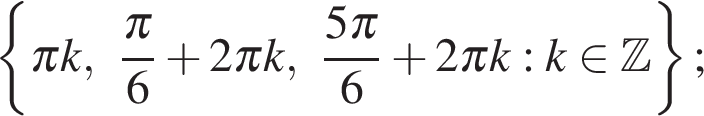 б)
б) 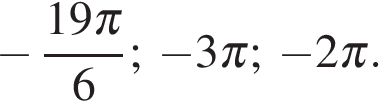
Источник: ЕГЭ — 2018. Основная волна 01.06.2018. Вариант 301 (C часть)., Задания 13 (С1) ЕГЭ 2018
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители, Тригонометрические формулы суммы или разности аргументов
Методы алгебры: Формулы двойного угла
24. Задание 13 № 520831
а) Решите уравнение: 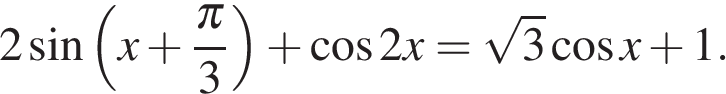
б) Определите, какие из его корней принадлежат отрезку 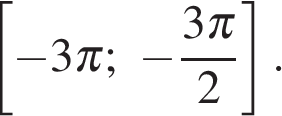
Решение.
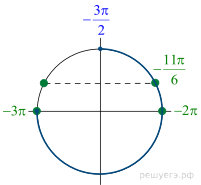 а) Запишем исходное уравнение в виде:
а) Запишем исходное уравнение в виде:
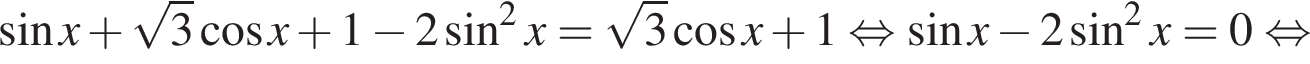
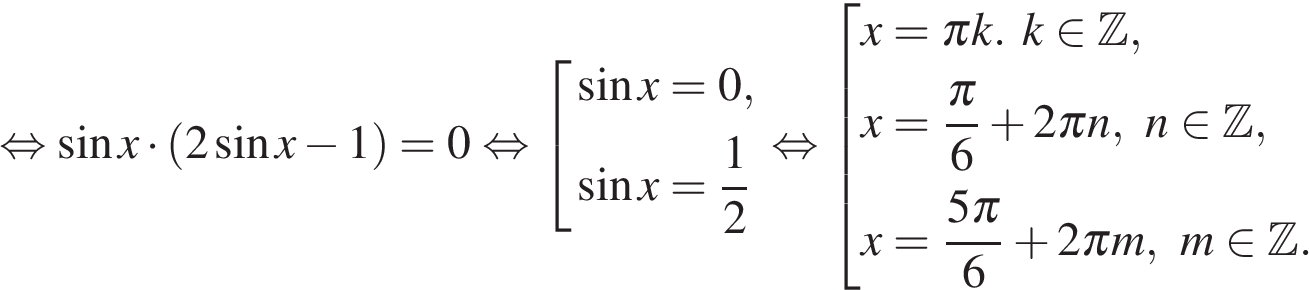
б) С помощью числовой окружности отберем корни, принадлежащие отрезку 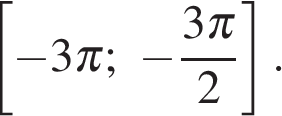 Получим числа:
Получим числа: 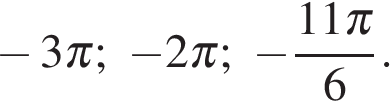
Ответ: а) 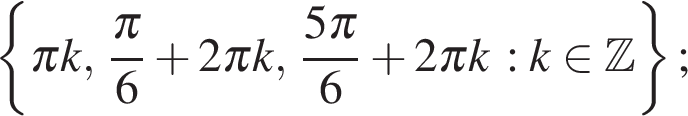 б)
б) 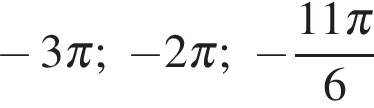 .
.
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
520831
а) 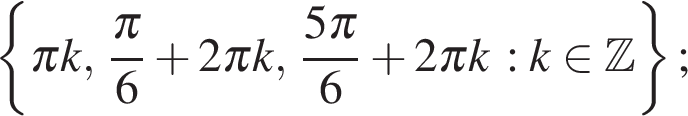 б)
б) 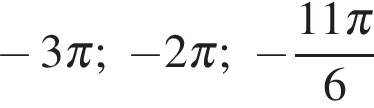 .
.
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Тригонометрические формулы суммы и разности аргументов, Формулы двойного угла
25. Задание 13 № 525068
а) Решите уравнение 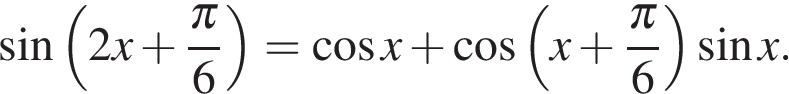
б) Найдите все корни этого уравнения, принадлежащие отрезку 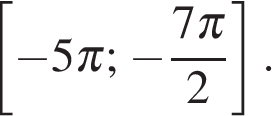
Решение.
а) Запишем исходное уравнение в виде

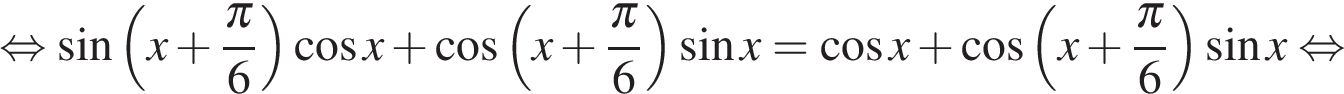
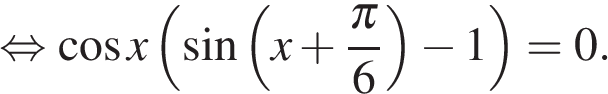
Значит, 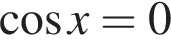 или
или 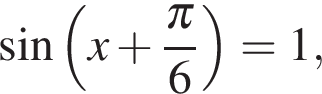 откуда
откуда 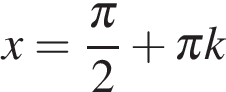 или
или 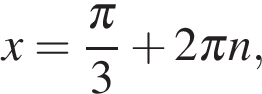 где
где 
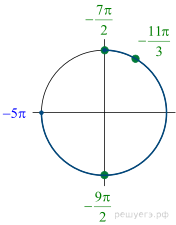
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 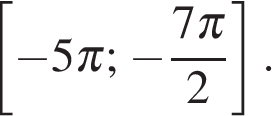 Получим числа
Получим числа 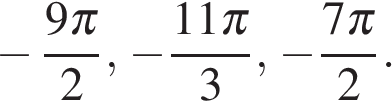
Ответ: а) 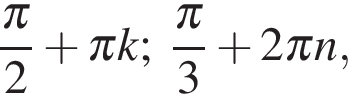 где
где  б)
б) 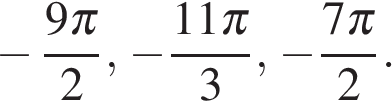
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
525068
а) 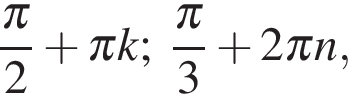 где
где  б)
б) 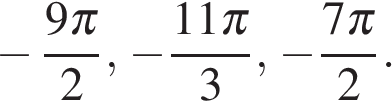
Раздел кодификатора ФИПИ/Решу ЕГЭ: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Тригонометрические формулы суммы и разности аргументов
26. Задание 13 № 548814
а) Решите уравнение 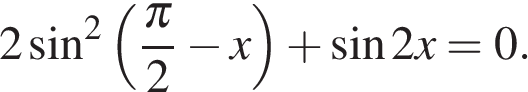
б) Укажите корни этого уравнения, принадлежащие отрезку 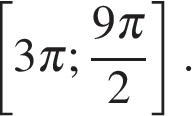
Решение.

а) Запишем исходное уравнение в виде:

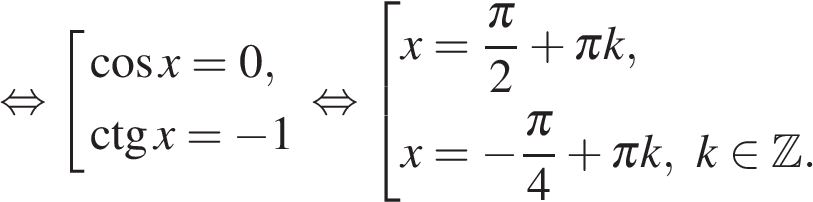
б) С помощью тригонометрической окружности отберем корни, принадлежащие указанному промежутку. Подходят корни 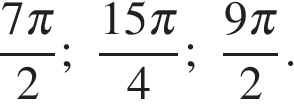
Ответ: а) 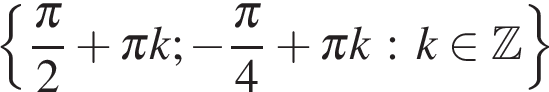 б)
б) 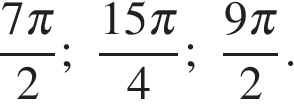
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
548814
а) 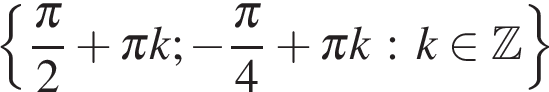 б)
б) 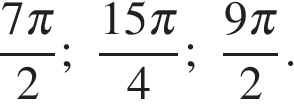
Источник: ЕГЭ по математике 25.07.2020. Резервный день. Вариант 2, Задания 13 ЕГЭ–2020
27. Задание 13 № 549973
а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие промежутку 
Решение.

а) Решим уравнение:
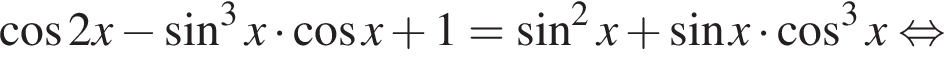
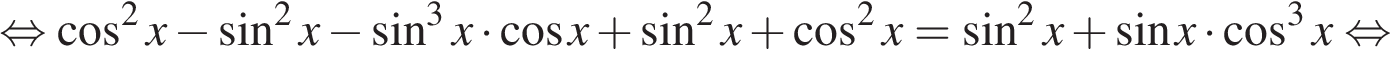

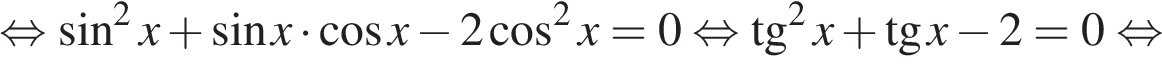
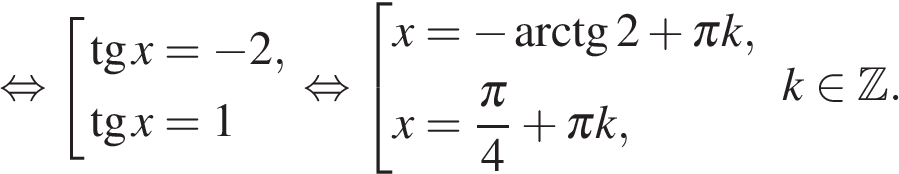
б) Отберём корни при помощи тригонометрической окружности. Заданному условию удовлетворяют корни  и
и 
Ответ: а)  б)
б) 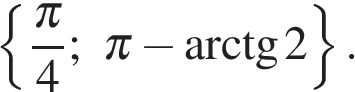
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
549973
а)  б)
б) 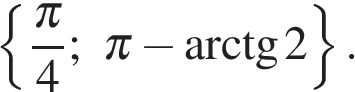
Источник: А. Ларин. Тренировочный вариант № 322 (часть C).
28. Задание 13 № 555715
а) Решите уравнение 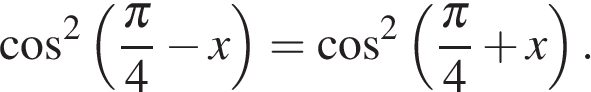
б) Найдите все его корни, принадлежащие отрезку 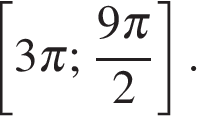
Решение.
а) Запишем исходное уравнение в виде:

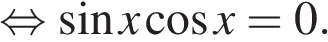
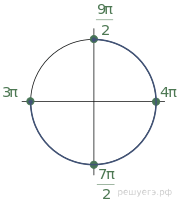
Таким образом,  следовательно,
следовательно, 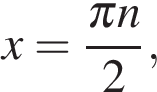

б) С помощью числовой окружности отберём корни, принадлежащие отрезку 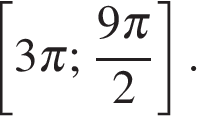 Получим корни (см. рис.):
Получим корни (см. рис.): 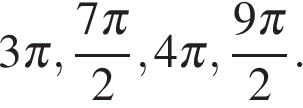
Ответ: а) 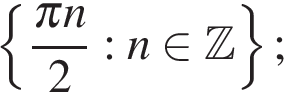 б)
б) 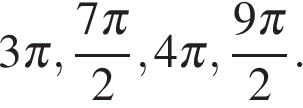
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
555715
а) 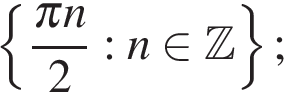 б)
б) 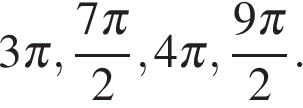
29. Задание 13 № 555967
а) Решите уравнение 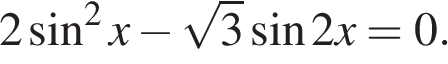
б) Найдите все его корни, принадлежащие отрезку 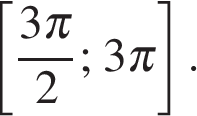
Решение.
а) Преобразуем уравнение:
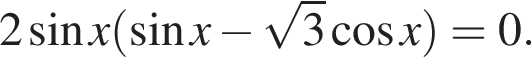
Получаем, что 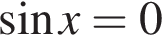 или
или 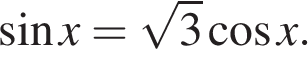 Из второго уравнения находим
Из второго уравнения находим 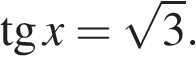 Следовательно,
Следовательно, 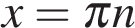 или
или 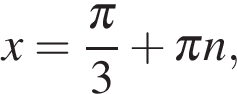

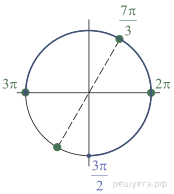
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 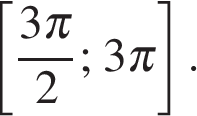 Получим корни (см. рис.):
Получим корни (см. рис.): 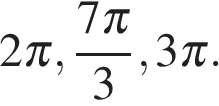
Ответ: а) 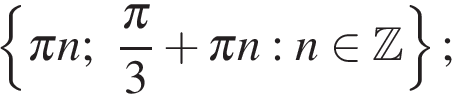 б)
б) 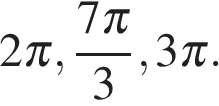
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
555967
а) 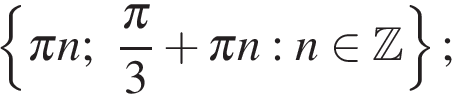 б)
б) 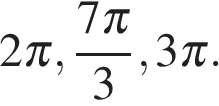
30. Задание 13 № 556336
а) Решите уравнение 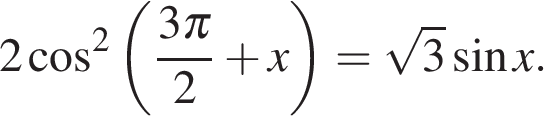
б) Найдите все его корни, принадлежащие отрезку 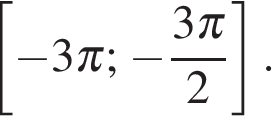
Решение.
а) Используя формулу приведения 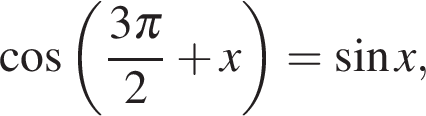 уравнение можно записать в виде
уравнение можно записать в виде
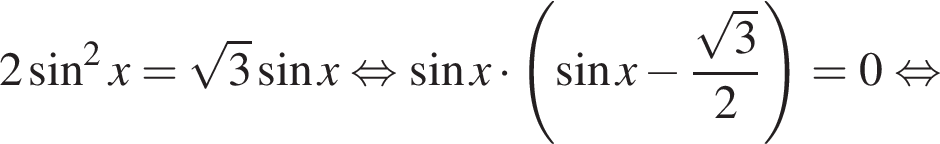
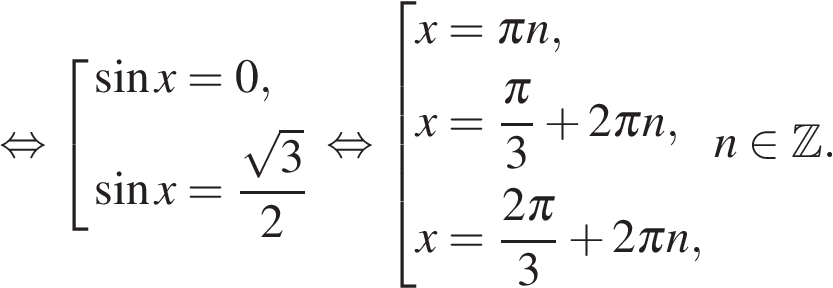
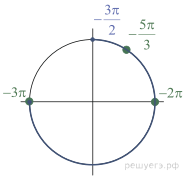
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 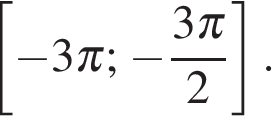 Получим корни (см. рис.):
Получим корни (см. рис.): 
Ответ: а) 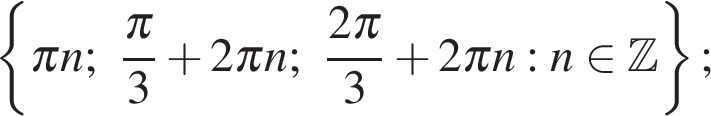 б)
б) 
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
556336
а) 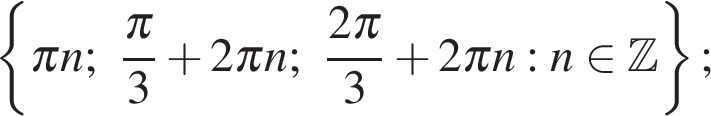 б)
б) 
31. Задание 13 № 559407
а) Решите уравнение 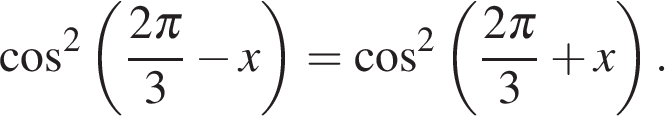
б) Найдите все его корни, принадлежащие отрезку 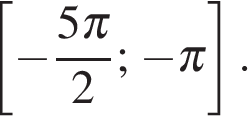
Решение.
а) Запишем исходное уравнение в виде:

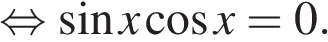
Таким образом,  следовательно,
следовательно, 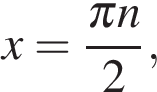

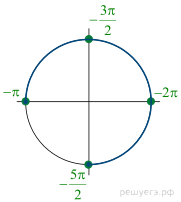
б) Корни, принадлежащие промежутку 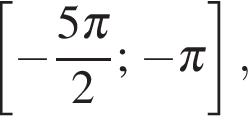 отберём с помощью
отберём с помощью
единичной окружности. Получаем: 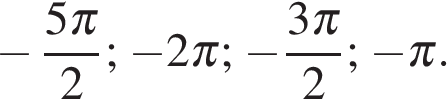
Ответ: а) 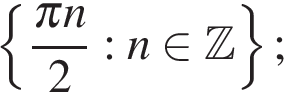 б)
б) 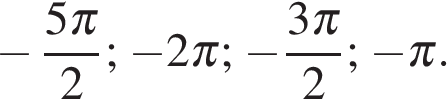
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
559407
а) 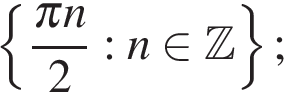 б)
б) 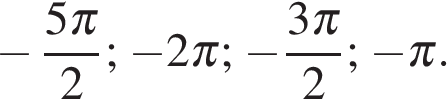
32. Задание 13 № 560137
а) Решите уравнение 
б) Найдите все его корни этого уравнения, принадлежащие отрезку 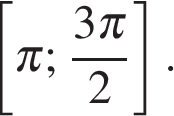
Решение.
а) Запишем исходное уравнение в виде:
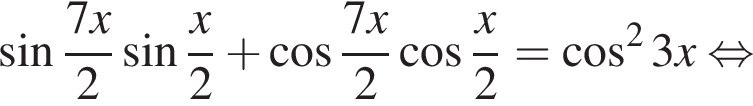
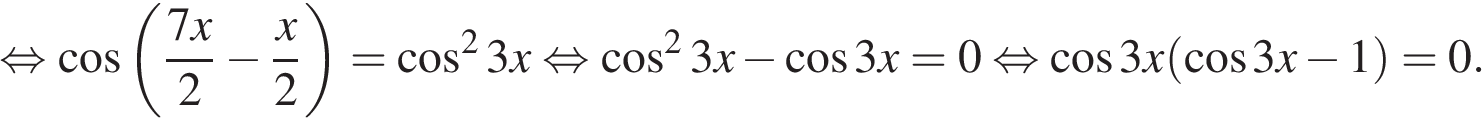
Следовательно,  или
или 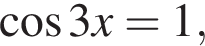 а значит,
а значит, 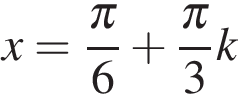 или
или 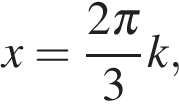

б) Корни, принадлежащие промежутку 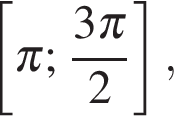 отберём с помощью
отберём с помощью
единичной окружности. Получаем: 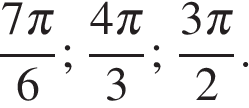
Ответ: а) 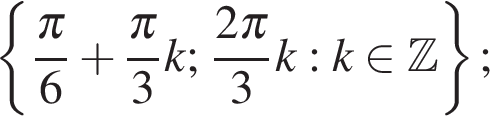 б)
б) 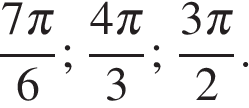
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
560137
а) 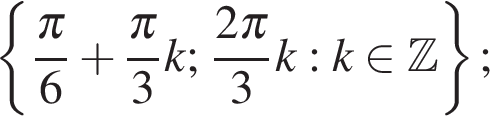 б)
б) 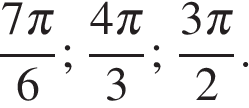
33. Задание 13 № 561175
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 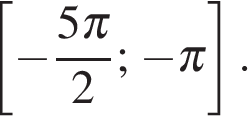







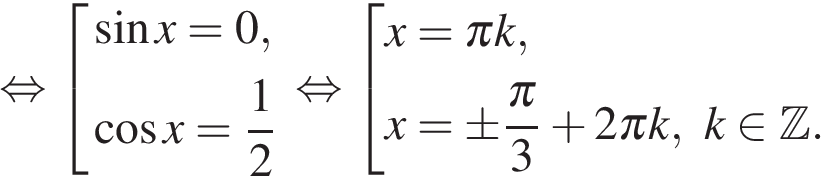

 а) Запишем уравнение в виде
а) Запишем уравнение в виде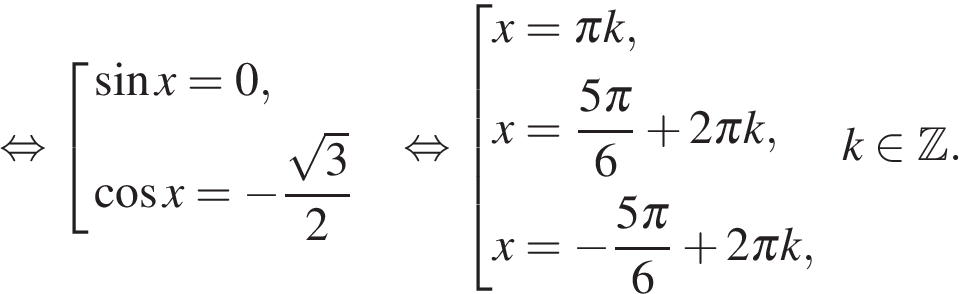

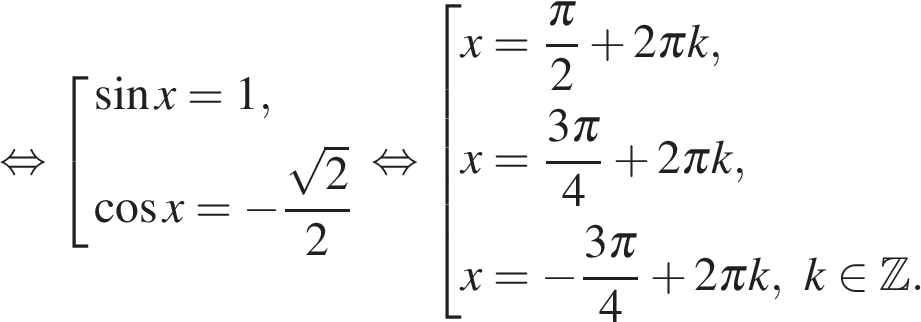
 а) Перенесём все члены в левую часть, преобразуем и разложим левую часть на множители:
а) Перенесём все члены в левую часть, преобразуем и разложим левую часть на множители: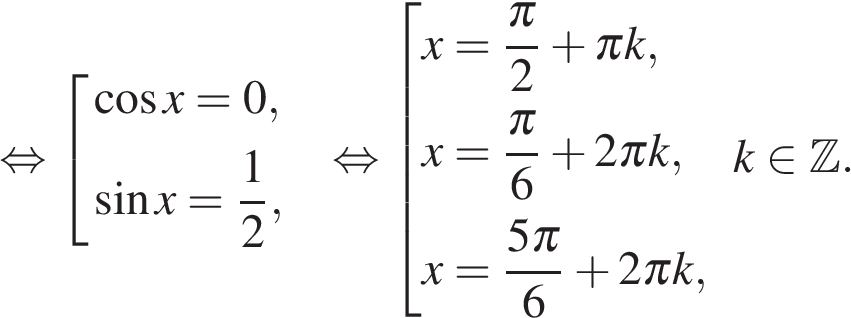

 а) Заметим, что
а) Заметим, что 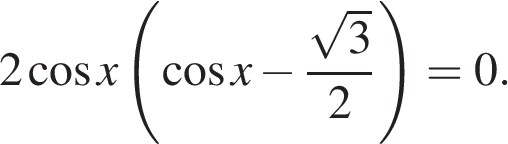 Значит, либо
Значит, либо 
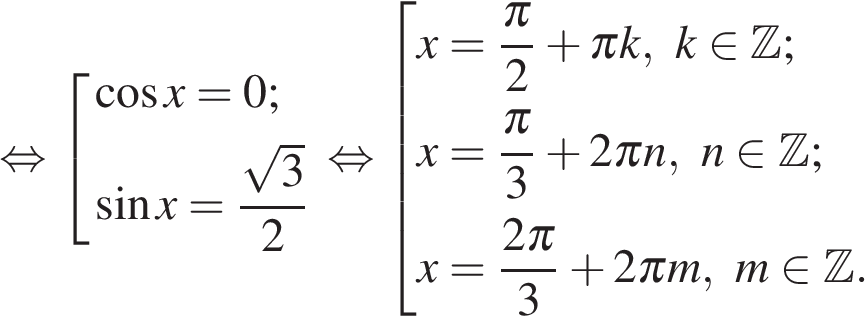
 а) Запишем уравнение в виде
а) Запишем уравнение в виде 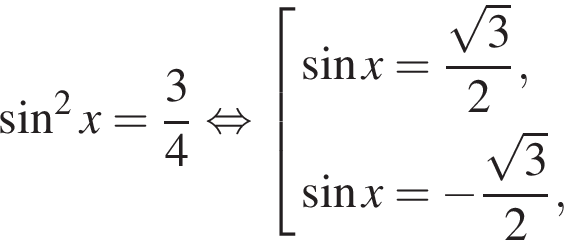 откуда
откуда 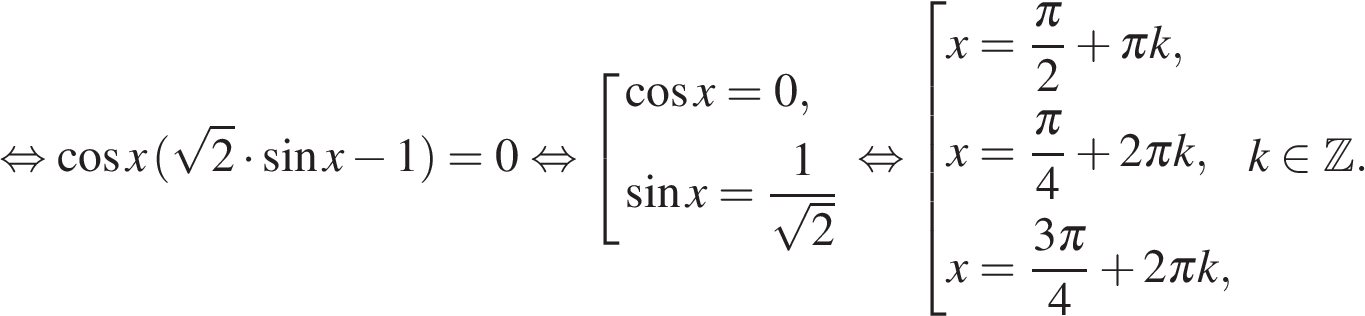


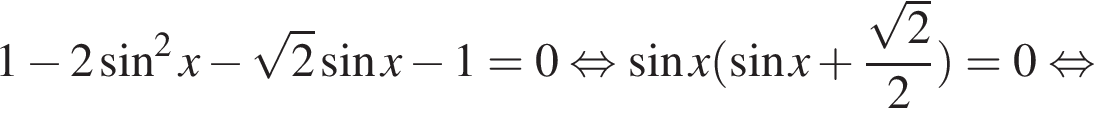
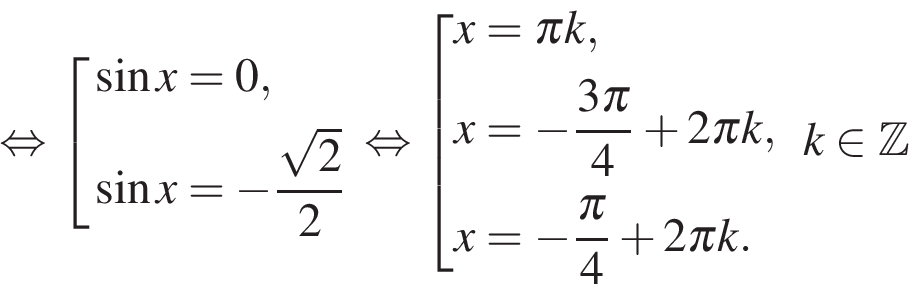

 а) Преобразуем уравнение :
а) Преобразуем уравнение :  а) Используя формулы приведения, получим уравнение, квадратное относительно косинуса:
а) Используя формулы приведения, получим уравнение, квадратное относительно косинуса: 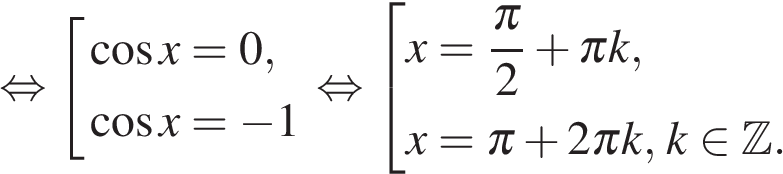
 Решим уравнение:
Решим уравнение: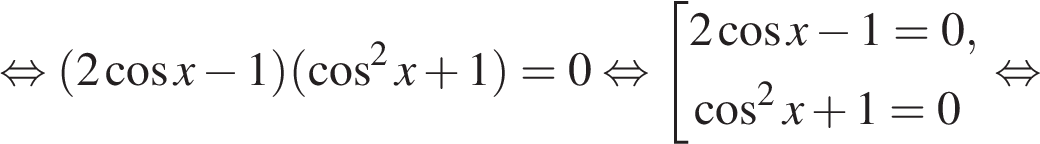
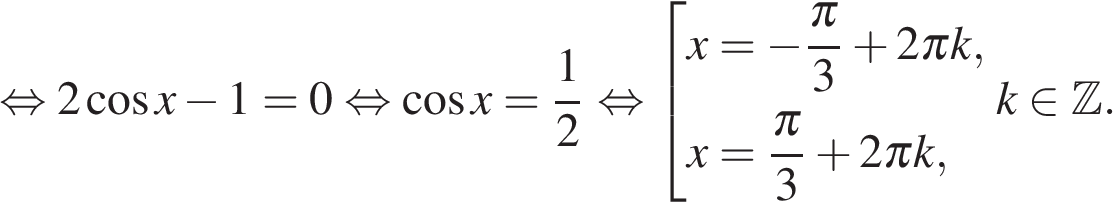
 а) Разложим левую часть на множители:
а) Разложим левую часть на множители: а) Запишем уравнение в виде:
а) Запишем уравнение в виде: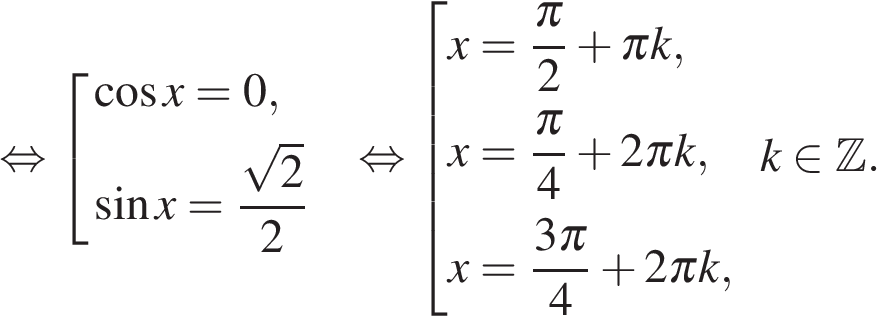
 а) Запишем исходное уравнение в виде:
а) Запишем исходное уравнение в виде: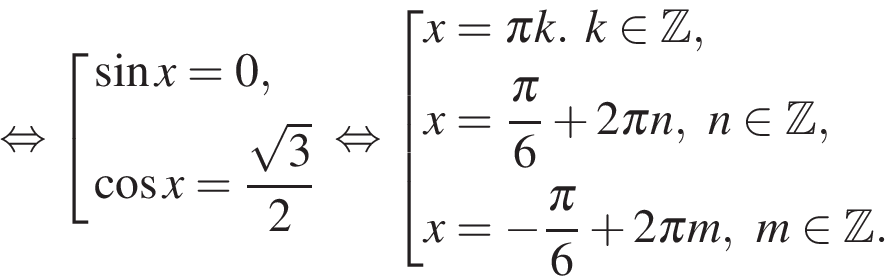
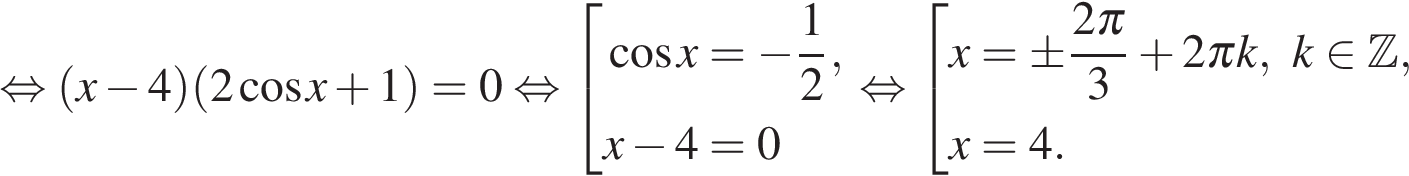
 При помощи числовой оси отберем корни, принадлежащие отрезку
При помощи числовой оси отберем корни, принадлежащие отрезку 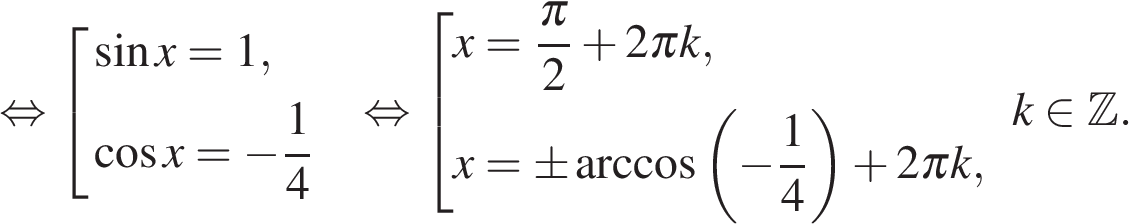

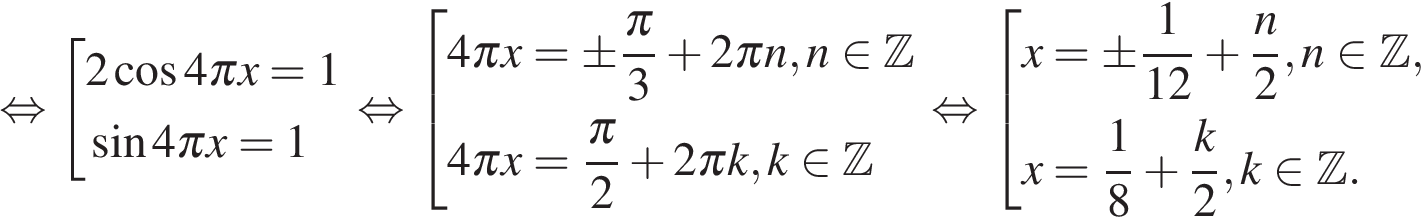

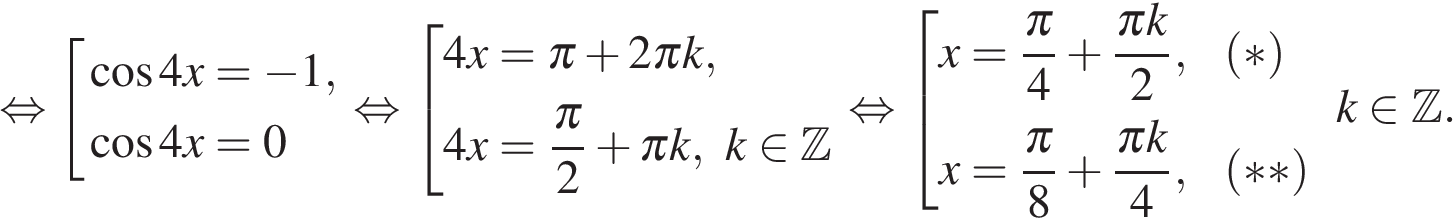
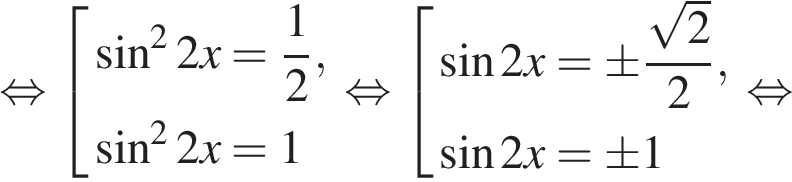
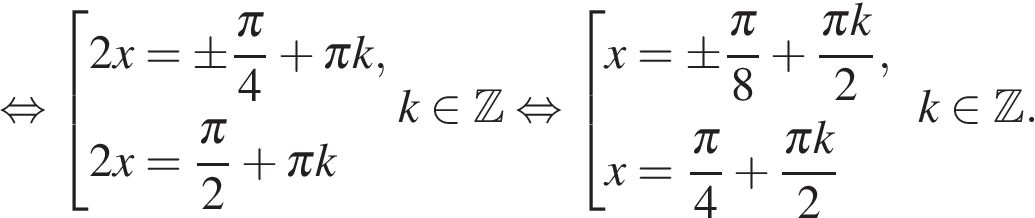

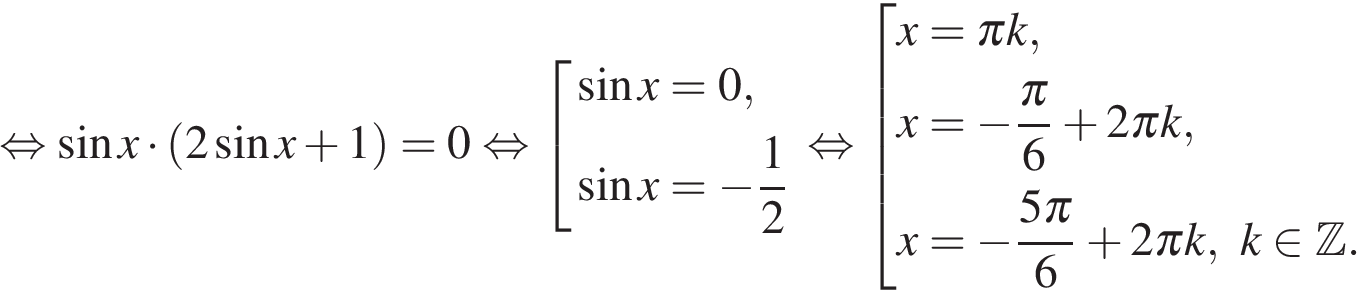

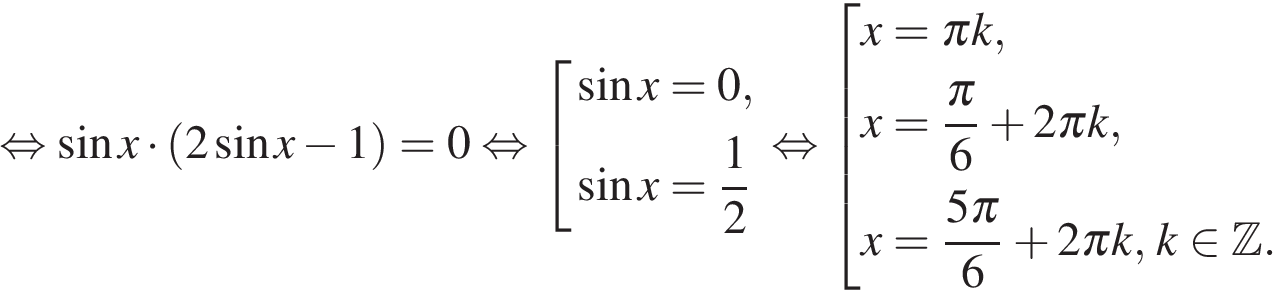
 а) Запишем исходное уравнение в виде:
а) Запишем исходное уравнение в виде: