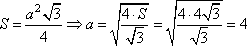ЕГЭ профильный уровень. Задание № 8 (новое). Стереометрия.

ЕГЭ профильный уровень.

Задание № 8 (новое). Стереометрия

1. Правильную четырехугольную пирамиду пересекает плоскость параллельная основанию пирамиды и проходящая через середину ее высоты. Найдите объем фигуры, начинающейся от вершины пирамиды и ограниченной секущей плоскостью, если объем исходной пирамиды равен 120.

Решение.

Так как секущая плоскость проходит через середину высоты пирамиды и параллельна ее основанию, то все линейные размеры полученной малой пирамиды в 2 раза меньше исходной пирамиды. Значит, объем малой пирамиды в  раз меньше объема V=120 исходной. Имеем:

Ответ: 15.

1.  Объем правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 равен 24√3. Длина бокового ребра равна 6. Найдите длину диагонали AD1.

Решение.

В основании правильной шестиугольной призмы лежит равносторонний шестиугольник, который можно разбить на 6 равносторонних треугольников.

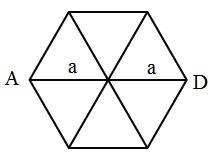
Площадь каждого такого треугольника, равна , а длина стороны:

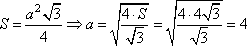
Рассмотрим прямоугольный треугольник ADD1, в котором катет , а катет DD1=6. Тогда по теореме Пифагора гипотенуза AD1, равна:

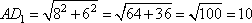
Ответ: 10.

1. Вокруг куба описан шар радиусом 18√3. Найдите длину стороны куба.

Решение.

Из рисунка видно, что диаметр шара  соответствует диагонали куба.

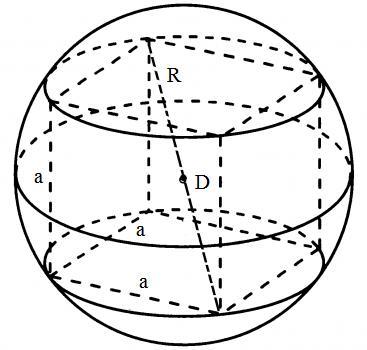
В то же время, диагональ куба выражается через сторону куба формулой 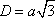, откуда

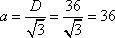
Ответ: 36.

1. Дан параллелепипед объемом 180 и высотой 5, в основании которого лежит квадрат. Найдите площадь его боковой поверхности.

Решение.

Найдем сначала площадь основания параллелепипеда из формулы его объема:

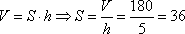
и, так как в основании лежит квадрат, то его стороны равны

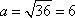
Тогда площадь боковой поверхности параллелепипеда, равна

Ответ: 120.

1. В сосуд, имеющим форму цилиндра, наливается жидкость до уровня 10 см. Известно, что площадь основания этого цилиндра равна 20 кв. см. После погружения детали в жидкость уровень жидкости увеличился в 1,5 раза. Найдите объем детали. Ответ дайте в куб. см.

Решение.

Начальный объем жидкости в цилиндре равен  куб. см. После погружения в нее детали объем стал равен

 куб. см.

Следовательно, объем детали равен:

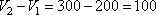 куб. см.

Ответ: 100.

1. Вокруг конуса высотой 9 описан шар. Образующие конуса пересекаются под углом 120º. Найдите диаметр шара.

Решение.

Сделаем дополнительное построение: проведем из точки A в точку D прямую, и так как CD – диаметр окружности, то прямые AC и AD пересекаются под углом 90º.

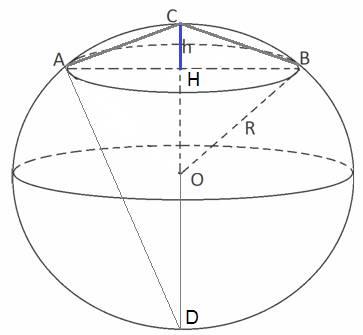
Рассмотрим прямоугольный треугольник ACD с прямым углом A и высотой AH. Для такого треугольника справедливо равенство:

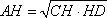
откуда

Так как образующие пересекаются под 120º, то угол ACH=120:2=60º и

и

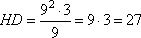
Получаем диаметр шара

Ответ: 36.

1. В правильной треугольной пирамиде высота равна 3, а сторона основания 12√3. Найдите длину бокового ребра пирамиды.

Решение.

В основании правильной треугольной пирамиды лежит равносторонний треугольник и высота MO делит в точке O отрезок AK в отношении 2:1, считая от вершины A.

Найдем высотку AK из прямоугольного треугольника AKC, в котором известна гипотенуза AC=12√3 и угол ACK=60º:

Тогда . Найдем длину бокового ребра AM из прямоугольного треугольника AOM. По теореме Пифагора, имеем:

Ответ: 5.

1. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1 с длиной бокового ребра 5√3 и ребром основания 4. Найдите объем фигуры ABEFA1F1.

Решение.

Из рисунка видно, что объем фигуры ABEFA1F1 равен половину объема призмы ABEFA1B1E1F1. Найдем сначала объем этой призмы по формуле

,

где h=AA1=5√3 – высота призмы;  - площадь ее основания ABEF.

Так как в основании правильной шестиугольной призмы лежит равносторонний шестиугольник, который можно составить из 6 равносторонних треугольников, то площадь основания ABEF образуется из 3 таких треугольников (см. рисунок ниже).

Площадь каждого треугольника можно найти по формуле

И площадь основания, равна:

Получаем объем призмы ABEFA1B1E1F1:

Тогда объем фигуры ABEFA1F1, равен:

Ответ: 90.

1. В куб объемом  вписан шар. Найдите объем шара.

Решение.

Из рисунка видно, что диаметр шара равен стороне куба. А сторону куба можно связать с его объемом по формуле:

Так как объем шара определяется по формуле , а

Получаем объем шара:

Ответ: 36.

1. Вокруг правильного четырехугольного параллелепипеда ABCDA1B1C1D1 высотой 73 описан шар. Диаметр шара равен 89. Найдите объем параллелепипеда.

Решение.

Сделаем дополнительные построения: проведем прямые MA1 и A1N, которые опираются на диаметр MN, а, значит, угол MA1N – прямой.

Рассмотрим прямоугольный треугольник MA1N, из прямого угла которого проведена высота A1H. По свойству прямоугольного треугольника для высоты A1H можно записать равенство:

Можно заметить, что NH=MK, а KH=73 и D=MN=89 по условию задания. Тогда

Находим A1H:

Тогда диагональ A1C1 квадрата A1B1C1D1, равна:

В результате получаем, что стороны в основании параллелепипеда, равны:

И его объем:

Ответ: 2628.

3