В 11. Постоянный ток в металлах. ЭДС. Закон Ома и Джоуля-Ленца. Правила Кирхгофа, их физический смысл.
Электрическим током называется всякое направленное движение электрических зарядов. Значит внутри проводника существует электрическое поле, характеризующееся напряженностью 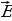 , которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами провода, несущего ток, должна существовать разность потенциалов U (напряжение или падение напряжения). Сила тока является функцией разности потенциалов
, которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами провода, несущего ток, должна существовать разность потенциалов U (напряжение или падение напряжения). Сила тока является функцией разности потенциалов 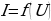 .
.
Основной характеристикой электрического тока является величина тока, численно равная количеству электричества, проходящего через поперечное сечение проводника в единицу времени
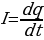 (5.1)
(5.1)
Если величина тока со временем не изменяется, то ток называется постоянным
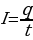 I=Const. (5.2)
I=Const. (5.2)
Электрический ток характеризуется различными действиями, которые не имеют места при покоящихся зарядах:
Прохождение электрического тока по проводнику приводит к нагреванию проводника - тепловое действие тока.
Магнитное действие тока впервые было открыто в 1820 г. Х.К. Эрстедом по отклонению магнитной стрелки, помещенной вблизи проводника с током.
За единицу тока в системе СИ принимают величину такого постоянного тока, при котором через поперечное сечение проводника за одну секунду протекает 1 кулон электричества. Эту единицу называют ампером.
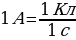 ; 1мА = 10-3 А; 1мкА = 10-6 А.
; 1мА = 10-3 А; 1мкА = 10-6 А.
Если концентрация (т.е. число частиц в единице объема) свободных электронов в данном проводнике n0, а скорость их направленного движения υ, то за время ∆t ( через поперечное сечение S переносится заряд
q = en0υ∆tS, (5.3)
где е - заряд электрона, тогда
I = en0υ∆tS. (5.4)
.
Плотностью тока называется величина, численно равная току, протекающему через единичную поверхность поперечного сечения проводника
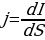 (5.5)
(5.5)
Учитывая выражение (5.4), имеем
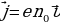 (5.6)
(5.6)
Плотность тока величина векторная, ее направление совпадает с вектором скорости направленного перемещения положительных зарядов в проводнике (в металлах  направлено антипараллельно вектору скорости электронов).
направлено антипараллельно вектору скорости электронов).
Сопротивление однородного проводника длиной l, площадью поперечного сечения S выражается
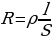 , (5.7)
, (5.7)
г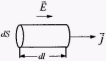 де ρ - удельное сопротивление вещества. Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью
де ρ - удельное сопротивление вещества. Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью
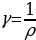 , (5.8)
, (5.8)
а величина, обратная сопротивлению, называется проводимостью проводника
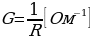 (5.9)
(5.9)
Н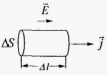 аиболее просты законы электрического тока для металлов. Хорошо выполняется закон Ома для участка цепи
аиболее просты законы электрического тока для металлов. Хорошо выполняется закон Ома для участка цепи 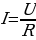 (5.10)
(5.10)
Найдем связь между вектором плотности тока  и напряженности поля
и напряженности поля 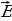 в некоторой точке проводника. В окрестности этой точки
в некоторой точке проводника. В окрестности этой точки
Рис. 5.1 мысленно выделим малый цилиндр, ориентированный вдоль линий напряженности (рис. 5.1).
Напряжение на длине ∆l цилиндра U = E∆l, сила тока через его сечение I = j∆S, а сопротивление цилиндра 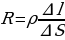 , подставив эти значения в закон Ома для участка цепи
, подставив эти значения в закон Ома для участка цепи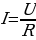 , получим
, получим 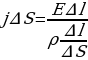 ; или
; или 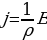 , так как направления векторов
, так как направления векторов  и
и 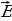 совпадают, то можно записать
совпадают, то можно записать
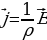 (5.11)
(5.11)
или
 (5.12)
(5.12)
- получили закон Ома в дифференциальной форме: плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление.
Рассмотрим, какие силы действуют на свободный электрон в проводнике. С одной стороны, это кулоновские силы взаимодействия между зарядами. Но они всегда приводят к такому перераспределению зарядов, при котором наступает равновесие. Следовательно, кулоновские силы не могут вызвать длительный процесс упорядоченного движения зарядов, т.е. они не являются причиной постоянного электрического тока.
Для того, чтобы упорядоченное движение электрических зарядов все время поддерживалось, необходимо действие каких-либо иных, неэлектростатических сил. Такие силы получили название сторонних сил. Сторонние силы вызывают разделение электрических зарядов внутри источника тока (гальванических элементов, аккумуляторов, электрических генераторов).
За счет поля сторонних сил электрические заряды внутри источника тока движутся против сил электростатического поля, в результате чего на концах внешней цепи все время поддерживается определенная разность потенциалов и в цепи идет постоянный электрический ток.
При этом особенностью сторонних сил является неравенство нулю циркуляции напряженности поля сторонних сил
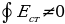 (5.13)
(5.13)
Максимальная разность потенциалов развиваемая источником называется электродвижущей силой (ЭДС), которая измеряется в вольтах. При включении источника в цепь эта разность потенциалов длительно поддерживается постоянной и в цепи создается постоянный ток. Источник ЭДС обладает некоторым внутренним сопротивлением. Поэтому при протекании тока разность потенциалов на зажимах источника может уменьшиться на величину Ir, где r - внутреннее сопротивление источника.
ЭДС направлена от отрицательного полюса к положительному. В разомкнутом источнике электрическое напряжение уравновешивается ЭДС, т.е.
при R = ∞, U = ε, R – сопротивление внешней цепи.
ЭДС - величина, измеряемая работой тока при перемещении единицы заряда по всей цепи
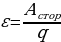 (5.14)
(5.14)
или ЭДС равна сумме падений напряжений на внешнем и внутреннем участках цепи.
ε = IR + Ir,
или
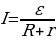 (5.15)
(5.15)
- закон Ома для замкнутой цепи. Закон Ома гласит: величина тока в замкнутой цепи прямо пропорциональна величине ЭДС, действующей в этой цепи, и обратно пропорциональна сумме внешнего и внутреннего сопротивлений.
При протекании тока в проводнике выделяется тепло
Q = UIt, (5.21)
так как по закону Ома U =IR, то можем записать
Q = RI2t. (5.22)
Это соотношение было установлено экспериментально Д.П. Джоулем и независимо от него Э. X. Ленцем и носит название закона Джоуля-Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
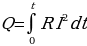 (5.23)
(5.23)
- интегральная форма закона Джоуля-Ленца.
Выделим в проводнике элементарный объем в виде цилиндра (рис. 5.2). Согласно закону Джоуля-Ленца за время dt в этом объеме выделится тепло
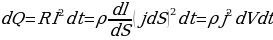 (5.24)
(5.24)
Рис. 5.2 где dV = dSdl - величина элементарного объема. Разделив выражение (5.24) на dV и dt, найдем количество теплоты, выделяющееся в единице объема в единицу времени (удельную тепловую мощность тока) Qуд = ρj2 (5.25)
Выражение (5.25) представляет собой дифференциальную форму закона Джоуля-Ленца.
Расчет сложных (разветвленных) цепей постоянного тока заключается в отыскании по заданным сопротивлениям участков цепи и приложенным к ним ЭДС, сил токов в каждом участке. Для решения этой задачи применяются правила Кирхгофа.
Первое правило: Алгебраическая сумма токов, сходящихся в узле, равна нулю:
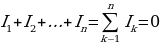 , (5.26)
, (5.26)
где n – число проводников, сходящихся в узле. Узлом в разветвленной цепи называется точка, в которой имеется более двух возможных направлений тока. Положительными считаются токи, подходящие к узлу, отрицательными – токи, отходящие от него.
Второе правило: В замкнутом контуре разветвленной цепи алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС всех источников в этом контуре:
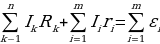 (5.27)
(5.27)
В 12. Колебательный контур. Свободные и вынужденные колебания. Резонанс. Генерация незатухающих колебаний.
Электрические и магнитные явления тесно связаны друг с другом. Простейшей системой, где это можно наблюдать, является колебательный контур - цепь, состоящая из катушки индуктивности L и конденсатора С.
Е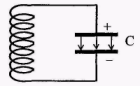 сли обкладки заряженного конденсатора соединить с концами катушки, конденсатор будет разряжаться и в контуре появится ток I. Энергия электрического поля конденсатора
сли обкладки заряженного конденсатора соединить с концами катушки, конденсатор будет разряжаться и в контуре появится ток I. Энергия электрического поля конденсатора 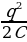 (где q
(где q
Рис. 15.1 – заряд на пластинах конденсатора) будет превращаться в энергию магнитного поля катушки 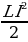 . Когда конденсатор полностью разрядится, ток в катушке и связанная с ним энергия магнитного поля достигнут максимума. Ток будет некоторое время поддерживаться за счет ЭДС самоиндукции, пока конденсатор не перезарядится. Энергия магнитного поля катушки преобразуется в энергию электрического поля перезаряженного конденсатора. Конденсатор снова начнет разряжаться, и явления повторятся в обратной последовательности. За время Т в контуре восстановится исходное состояние. Возникают периодические электрические колебания, сопровождающиеся превращением электрической энергии в магнитную и обратно.
. Когда конденсатор полностью разрядится, ток в катушке и связанная с ним энергия магнитного поля достигнут максимума. Ток будет некоторое время поддерживаться за счет ЭДС самоиндукции, пока конденсатор не перезарядится. Энергия магнитного поля катушки преобразуется в энергию электрического поля перезаряженного конденсатора. Конденсатор снова начнет разряжаться, и явления повторятся в обратной последовательности. За время Т в контуре восстановится исходное состояние. Возникают периодические электрические колебания, сопровождающиеся превращением электрической энергии в магнитную и обратно.
Колебания с периодом Т испытывают заряд q на обкладках конденсатора, разность потенциалов между ними, сила тока в контуре, напряженность электрического поля конденсатора и индукция магнитного поля катушки.
Составим уравнение колебаний, например, заряда на обкладках конденсатора и определим период этих колебаний. Примем, что сопротивление R контура очень мало и потерями энергии в контуре можно пренебречь. При этом полная энергия электрического и магнитного полей с течением времени не изменяется:
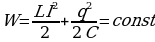 . (15.1)
. (15.1)
После преобразований получим дифференциальное уравнение собственных колебаний:
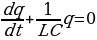 (15.2)
(15.2)
Электрические колебания, происходящие в колебательном контуре без воздействия внешних ЭДС, получили название собственных или свободных электрических колебаний.
Введя обозначения 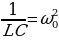 , приходим к следующей записи:
, приходим к следующей записи:
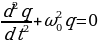 (15.3)
(15.3)
г де ω0 — собственная частота контура. Получили уравнение колебаний заряда q на обкладках конденсатора. Решение уравнения (15.3) имеет вид:
де ω0 — собственная частота контура. Получили уравнение колебаний заряда q на обкладках конденсатора. Решение уравнения (15.3) имеет вид:
q = q0cos(ω0t + φ), (15.4)
где q0 - амплитудное значение заряда, ω0 – циклическая частота собственных колебаний, φ – фаза колебаний. Дифференциальное уравнение (15.3) не отличается от уравнения колебаний гармонического осциллятора:
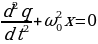 (15.5)
(15.5)
где х – смещение точки от положения равновесия.
Заряд q и все перечисленные выше электрические величины будут гармонически (по закону синуса или косинуса) изменяться в колебательном контуре во времени с частотой 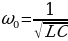 , а период этих колебаний определяется формулой Томсона:
, а период этих колебаний определяется формулой Томсона:
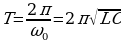 (15.6)
(15.6)
Напряжение на конденсаторе отличается от заряда множителем 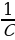 :
:
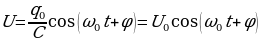 . (15.7)
. (15.7)
Продифференцировав выражение (15.4) по времени, получим выражение для силы тока:
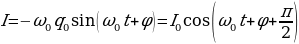 . (15.8)
. (15.8)
Таким образом, сила тока опережает по фазе напряжение на конденсаторе на 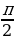 .
.
Из выражений (15.7) и (15.8) следует, что 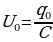 ,
, 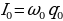 . Используя выражение
. Используя выражение 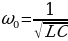 , получим
, получим 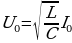 . (15.9)
. (15.9)
В реальном колебательном контуре (R ≠ 0) свободные электромагнитные колебания являются затухающими. Уравнение колебаний в данном контуре будет:
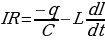 . (15.10)
. (15.10)
Дифференциальное уравнение затухающих колебаний:
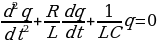 . (15.11)
. (15.11)
Приняв во внимание, что 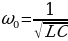 и введя обозначения
и введя обозначения 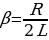 (β коэффициент затухания), получим выражение (15.11) в виде:
(β коэффициент затухания), получим выражение (15.11) в виде:
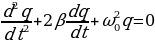 (15.12)
(15.12)
При условии, что β2 ω02 , то есть 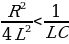 , решение уравнения (15.12) имеет вид:
, решение уравнения (15.12) имеет вид:
q = q0e-βtcos (ωt + φ), (15.13)
где 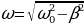 . Подставив значения
. Подставив значения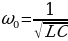 и
и 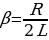 , получим, что
, получим, что 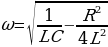 . (15.14)
. (15.14)
Таким образом, частота затухающих колебаний ω меньше собственной частоты ω0. Разделив функцию (15.13) на емкость С, получим напряжение на конденсаторе:
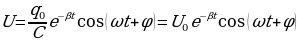 . (15.15)
. (15.15)
Чтобы найти силу тока I, продифференцируем выражение (15.13) по времени:
I = q0e-βt[-β cos(ωt+φ) - ω sin(ωt+φ)]. (15.16)
произведя преобразования (15.16), получим
I = I0e-βt cos(ωt+φ+α). (15.17)
так как coaα , а sinα 0, то значение а заключено в пределах от 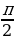 до π.
до π.
Таким образом, при наличии в контуре активного сопротивления R сила тока опережает по фазе напряжение на конденсаторе более чем на 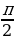 (при R = О опережение составляет
(при R = О опережение составляет 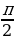 ).
).
Кроме коэффициента β для характеристики затухающих колебаний пользуются логарифмическим декрементом затухания δ, который равен натуральному логарифму отношения амплитуд колебаний, взятых через период Т:
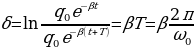 . (15.18)
. (15.18)
Величина 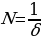 определяет число периодов, за которое амплитуда колебаний убывает в е раз.
определяет число периодов, за которое амплитуда колебаний убывает в е раз.
Ч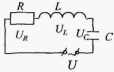 тобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний нужно включить последовательно с элементами контура переменную ЭДС или, разорвав контур, подать на образовавшиеся контакты переменное напряжение U = U0cosωt
тобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний нужно включить последовательно с элементами контура переменную ЭДС или, разорвав контур, подать на образовавшиеся контакты переменное напряжение U = U0cosωt
Для контура (рис. 15.2) можем записать 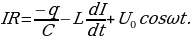 (15.20)
(15.20)
Произведя преобразования, получим дифференциальное уравнение вынужденных колебаний:
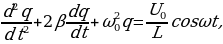 (15.21)
(15.21)
где 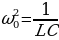 ,
, 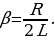
Решение уравнения (15.21) имеет вид
q = q0cos(ωt-ψ) , (15.22)
где ψ – начальная фаза,
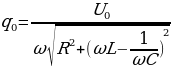 (15.23)
(15.23) 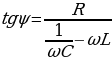 . (15.24)
. (15.24)
П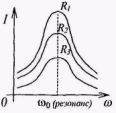 родифференцировав выражение (15.22) по t, найдем силу тока I в контуре:
родифференцировав выражение (15.22) по t, найдем силу тока I в контуре:
Рис. 15.2
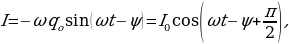 или
или
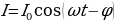 , (15.25)
, (15.25)
г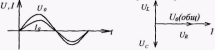 де
де 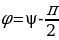 есть сдвиг по фазе между током и напряжением, тогда
есть сдвиг по фазе между током и напряжением, тогда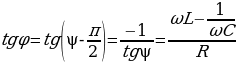 (15.26)
(15.26)
Из выражения (15.26) следует, что ток отстает по фазе от напряжения 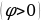 в том случае, когда
в том случае, когда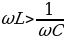 , и опережает напряжение
, и опережает напряжение 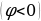 при условии, что
при условии, что 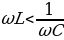 .
.
С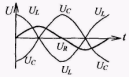 огласно выражения (15.23)
огласно выражения (15.23) 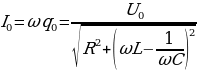 (15.27)
(15.27)
Представим соотношение (15.20) в виде 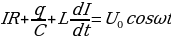 (15.28)
(15.28)
Произведение IR равно напряжению на активном сопротивлении 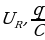 - напряжение на конденсаторе
- напряжение на конденсаторе 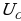 , выражение
, выражение 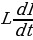 определяет напряжение на индуктивности
определяет напряжение на индуктивности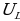 . С учетом этого можно записать
. С учетом этого можно записать 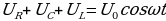 (15.29)
(15.29)
Сумма напряжений на отдельных элементах контура в каждый момент времени равна напряжению, приложенному извне.
В соответствии с (15.25) напряжение на активном сопротивлении 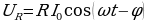 (15 30)
(15 30)
Разделив выражение (15.22) на емкость, получим напряжение на конденсаторе:
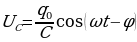 (15.31)
(15.31)
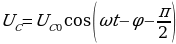 (15.32)
(15.32)
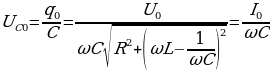
 .
.
Умножив производную функцию (15.25) на L, получим напряжение на индуктивности:
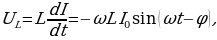 (15.33)
(15.33) 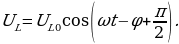 (15.34)
(15.34) 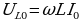
Сопоставление выражений (15.25), (15.30), (15.31) и (15.33) показывает, что напряжение на емкости отстает по фазе от силы тока на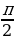 , а напряжение на индуктивности опережает ток на
, а напряжение на индуктивности опережает ток на 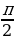 . Напряжение на активном сопротивлении изменяется в фазе с током.
. Напряжение на активном сопротивлении изменяется в фазе с током.
Установившиеся вынужденные электрические колебания происходят с частотой, равной частоте внешней вынуждающей силы, независимо от величины параметров самой колеблющейся системы, то есть независимо от R, L, С. Этим объясняется, что в цепях переменного тока колебания тока I (или заряда q на конденсаторе) всегда происходят с частотой ЭДС генератора, независимо от того, какова эта цепь. Амплитуда же колебаний и сдвиг фаз, наоборот, существенно зависят от параметров цепи.
Электрической автоколебательной системой является ламповый генератор незатухающих электрических колебаний.
В реальном контуре  из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.
из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.
Колебательный контур включен в анодную цепь лампы. При ее замыкании конденсатор заряжается и в контуре возбуждаются свободные колебания. Протекающий по катушке переменный ток наводит в связанной с ней индуктивно катушке обратной связи - переменную ЭДС. Переменное напряжение с этой катушки поступает на промежуток сетка-катод. Изменения сеточного напряжения вызывают изменения анодного тока с частотой, равной частоте  свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.
свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.
При последовательном соединении активного сопротивления R, реактивных сопротивлений (индуктивного L и ёмкостного С) в цепи действует переменная ЭДС, изменяющаяся по закону ε = ε0sinωt и
Рис 14.10 I=I0sinωt . При изменении частоты ω изменяется амплитуда тока I и сдвиг фаз φ. При частоте ω = ω0, определяемой условием 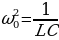 , реактивное сопротивление
, реактивное сопротивление 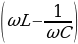 обращается в нуль в законе Ома
обращается в нуль в законе Ома 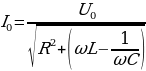 , сила тока I при этом достигает максимального значения
, сила тока I при этом достигает максимального значения 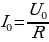 , контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ.
, контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ.
Рис. 14.11 Такой резонанс называется резонансом напряжений.
Рис. 14.12
Напряжение на L и С сдвинуты по фазе на 180°, т.е. компенсируют друг друга (рис. 14.13). При параллельном соединении L и С, при соотношении 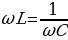 , сдвиг фаз φ становится равным нулю и,
, сдвиг фаз φ становится равным нулю и,
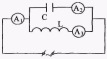
Рис. 14.13 следовательно, контур ведет себя как чисто активное сопротивление. Этот частный случай вынужденных колебаний в разветвленной цепи называется резонансом токов
(рис. 14.14). Оба тока IL и IC обладают разностью фаз близкой к 180°, т.е. находятся в противофазах. При резонансе полный ток становится наименьшим, а сопротивление контура достигает наибольшего значения 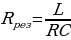 . При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей.
. При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей.
Резонанс напряжений широко используется в радиотехнике для выделения из многих сигналов различных радиостанций только одной частоты (настроиться на одну частоту). Вредное влияние резонанса в электрических цепях
Рис. 14.14 проявляется в тех случаях, когда в цепи возникают большие токи или напряжения (когда цепи не предусмотрены на работу в условиях резонанса), происходит расплавление проводов, пробой изоляции и т.д.
В 13. Переменный ток. Сопротивление, емкость, индуктивность в цепи переменного тока. Работа и мощность в цепи переменного тока.
Э лектрический ток, величина которого изменяется со временем, называется переменным. Для того, чтобы в замкнутом контуре существовал переменный ток, в нем должна существовать переменная ЭДС. Простейшим способом получения переменной ЭДС является вращение проводящей рамки в постоянном магнитном поле.
лектрический ток, величина которого изменяется со временем, называется переменным. Для того, чтобы в замкнутом контуре существовал переменный ток, в нем должна существовать переменная ЭДС. Простейшим способом получения переменной ЭДС является вращение проводящей рамки в постоянном магнитном поле.
Если величина магнитной индукции 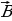 , то
, то
Рис. 14.1 поток индукции через площадь рамки в произвольный момент времени t Ф = BScosφ = Ф0cosφ (14.1)
где φ – угол между вектором 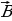 и нормалью к плоскости рамки. При равномерном вращении рамки с угловой скоростью ω, φ=ωt, поэтому Ф = Ф0cosωt. Так как величина магнитного потока изменяется со временем, то в рамке возникает ЭДС индукции
и нормалью к плоскости рамки. При равномерном вращении рамки с угловой скоростью ω, φ=ωt, поэтому Ф = Ф0cosωt. Так как величина магнитного потока изменяется со временем, то в рамке возникает ЭДС индукции 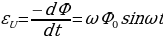 (14.2), так как ωФ0 = ε0, то ε = ε0sinωt .
(14.2), так как ωФ0 = ε0, то ε = ε0sinωt .
С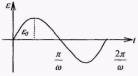 ледовательно ЭДС изменяется со временем по синусоидальному закону с циклической частотой ω равной скорости вращения рамки. Период изменения ЭДС равен периоду вращения рамки
ледовательно ЭДС изменяется со временем по синусоидальному закону с циклической частотой ω равной скорости вращения рамки. Период изменения ЭДС равен периоду вращения рамки 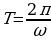 , а амплитудное значение ЭДС ε0 пропорционально скорости вращения ω. Рассмотренный принцип лежит в основе
, а амплитудное значение ЭДС ε0 пропорционально скорости вращения ω. Рассмотренный принцип лежит в основе
Рис. 14.2 работы генераторов переменного тока. На этом же принципе, но с использованием коллектора работают динамо-машины, дающие выпрямленную ЭДС.
Д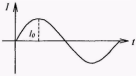 ействующее (эффективное) значение переменного тока равно максимальному (амплитудному l0) деленному на корень из двух (
ействующее (эффективное) значение переменного тока равно максимальному (амплитудному l0) деленному на корень из двух (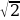 )
)
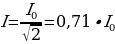 (14.3) Аналогично
(14.3) Аналогично 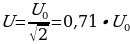 (14.4)
(14.4)
Рис. 14.3 Среднее значение переменного тока I = I0sinωt. За период значение переменного тока равно нулю.
а) (R)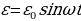 - ЭДС изменяется по синусоидальному закону, ток I- так же
- ЭДС изменяется по синусоидальному закону, ток I- так же 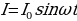 ,L = 0,С = 0.
,L = 0,С = 0.
Амплитудное значения тока 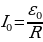
ЭДС и сила тока одновременно достигают максимальных значений и одновременно обращаются в нуль.
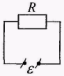
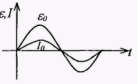
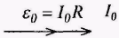
Рис. 14.4
б) (L)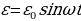 по второму правилу Кирхгофа
по второму правилу Кирхгофа 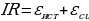 , т.к.
, т.к. 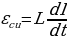 то
то 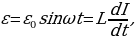
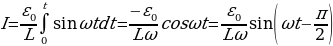
Ток отстает по фазе от ε на 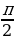 . Амплитудное значение тока
. Амплитудное значение тока 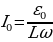
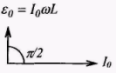
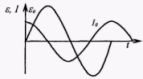
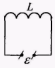
Рис. 14.5
в) (С), 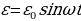 по второму правилу Кирхгофа
по второму правилу Кирхгофа 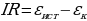 (т.к.
(т.к. 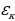 направлено противоположно
направлено противоположно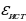 )
) 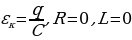 то
то 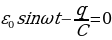 т.к.
т.к. 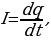 то
то
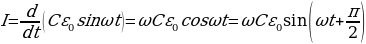 I опережает ε на
I опережает ε на 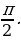
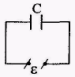
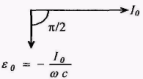
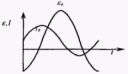
Рис. 14.6
г)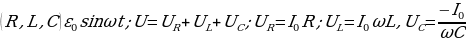
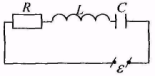
Рис 14.7
Рассмотрим чему равна работа, совершаемая в цепи при наличии в ней переменного тока.
Если в цепи имеется только активное сопротивление, вся работа тока в этом случае превращается в тепло. Пусть напряжение на концах цепи 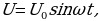 сила тока изменяется по закону
сила тока изменяется по закону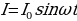 . В течение малого промежутка времени переменный ток можно рассматривать как ток постоянный, и поэтому мгновенная мощность переменного тока
. В течение малого промежутка времени переменный ток можно рассматривать как ток постоянный, и поэтому мгновенная мощность переменного тока
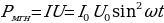 (14.8)
(14.8)
Работа переменного тока за малое время dt
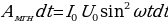 (14.9)
(14.9)
а за время полного периода Т:
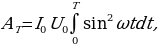 (14.10) но
(14.10) но
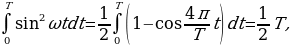 поэтому
поэтому
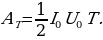 (14.11) Средняя мощность:
(14.11) Средняя мощность: 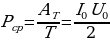 (14.12)
(14.12)
Вычислим среднюю мощность переменного тока, когда цепь содержит не только активное сопротивление R, но и реактивные. Между током и напряжением существует разность фаз. Работа совершаемая во внешней цепи за время dt равна 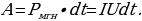
Напряжение Uможем разложить на две составляющие: активную 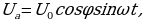 колеблющуюся в фазе с током, и реактивную
колеблющуюся в фазе с током, и реактивную 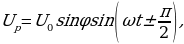 смещенную по фазе относительно тока на
смещенную по фазе относительно тока на 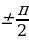 . При вычислении работы за полный период Т получим тоже два слагаемых. Одно из них, обусловленное реактивной составляющей напряжения UP, равно нулю, так как
. При вычислении работы за полный период Т получим тоже два слагаемых. Одно из них, обусловленное реактивной составляющей напряжения UP, равно нулю, так как
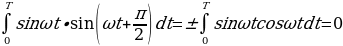 (14.13)
(14.13)
Полная работа за период определяется только активной составляющей напряжения
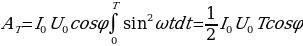 (14.14) Средняя мощность
(14.14) Средняя мощность 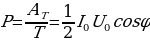 (14.15)
(14.15)
Вводя действующие значения I, U, получим 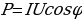 (14.16) т.е. выделяемая в цепи мощность зависит не только от силы тока и напряжения, но еще и от сдвига фаз между напряжением и током. Косинус угла
(14.16) т.е. выделяемая в цепи мощность зависит не только от силы тока и напряжения, но еще и от сдвига фаз между напряжением и током. Косинус угла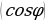 в электротехнике называют коэффициентом мощности.
в электротехнике называют коэффициентом мощности.
В 17. Шкала электромагнитных волн. Плоская монохроматическая волна. Скорость распространения волн. Ориентация векторов Е и Н в волне.
17. Шкала электромагнитных волн. Плоская монохроматическая волна. Скорость распространения волн. Ориентация векторов Е и Н в волне.
П ериодическое изменение электрического и магнитного поля в некоторой области пространства дает начало цепи последовательных взаимосвязанных превращений этих полей, захватывающих все новые области пространства. Оба эти поля являются вихревыми, причем векторы
ериодическое изменение электрического и магнитного поля в некоторой области пространства дает начало цепи последовательных взаимосвязанных превращений этих полей, захватывающих все новые области пространства. Оба эти поля являются вихревыми, причем векторы 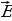 и
и 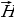 расположены во взаимно перпендикулярных плоскостях. Распространяющееся в пространстве периодически меняющееся электромагнитное поле образует электромагнитную волну. Из уравнений Д.К. Максвелла следует, что для плоской монохроматической электромагнитной волны, распространяющейся вдоль оси r имеем:
расположены во взаимно перпендикулярных плоскостях. Распространяющееся в пространстве периодически меняющееся электромагнитное поле образует электромагнитную волну. Из уравнений Д.К. Максвелла следует, что для плоской монохроматической электромагнитной волны, распространяющейся вдоль оси r имеем:
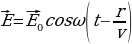 ,
, 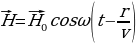 , где
, где 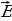 и
и 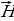 мгновенные, а
мгновенные, а 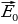 и
и 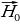 – амплитудные значения напряженности электрического и магнитного полей, ω – циклическая частота колебаний, υ – фазовая скорость волны. Векторы
– амплитудные значения напряженности электрического и магнитного полей, ω – циклическая частота колебаний, υ – фазовая скорость волны. Векторы 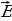 и
и 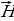 колеблются с одинаковой частотой и фазой, перпендикулярны вектору скорости
колеблются с одинаковой частотой и фазой, перпендикулярны вектору скорости 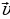 , указывающему направление распространения волны (рис. 17.1)
, указывающему направление распространения волны (рис. 17.1)
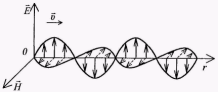
Рис. 17.1
Покажем, что существование электромагнитных волн вытекает из уравнений Д.К. Максвелла. В случае однородной нейтральной (ρ = 0) непроводящей (j = 0) среды с постоянными проницаемостями ε и μ 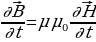 ,
, 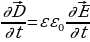 ,
, 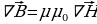 ,
, 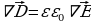
Поэтому уравнения Д.К. Максвелла 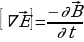 (17.1),
(17.1), 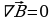 (17.2),
(17.2), 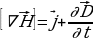 (17.3),
(17.3),
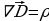 (17.4) можно записать следующим образом
(17.4) можно записать следующим образом 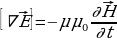 (17.5),
(17.5), 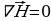 (17.6),
(17.6), 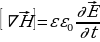 (17.7),
(17.7), 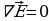 (17.8)
(17.8)
Возьмем ротор от обеих частей уравнения (17.5), произведя преобразования, учитывая, что 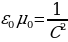 раскрыв оператор Лапласа, получим
раскрыв оператор Лапласа, получим 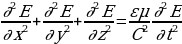 (17.9)
(17.9)
Взяв ротор от обеих частей уравнения (17.7) и, произведя аналогичные преобразования, получим
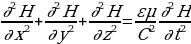 (17.10)
(17.10)
Уравнения (17.9) и (17.10) неразрывно связаны друг с другом, так как они получены из уравнений (17.5) и (17.7), каждое из которых содержит и 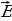 и
и 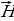 .
.
Уравнения (17.9) и (17.10) представляют собой типичные волновые уравнения. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну. Корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны. Следовательно, уравнения (17.9) и (17.10) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна 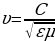 (17.11)
(17.11)
В вакууме (то есть при ε = 1, μ = 1) скорость электромагнитных волн совпадает со скоростью света 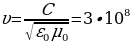 (м/с)
(м/с)
Величина 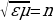 называется абсолютным показателем преломления среды и показывает, во сколько раз скорость электромагнитных волн в вакууме больше их скорости в данной среде.
называется абсолютным показателем преломления среды и показывает, во сколько раз скорость электромагнитных волн в вакууме больше их скорости в данной среде.
Источником электромагнитных волн являются движущиеся с ускорением заряженные частицы и изменяющиеся во времени электрические токи.
Процесс испускания электромагнитных волн источником называется излучением электромагнитных волн, а источник излучения - излучающей системой. Электромагнитное поле волны называется полем излучения.
Примером излучающей системы является вибратор Г.Герца, который был изобретен в 1888г. Вибратор представляет собой металлический стержень с двумя одинаковыми шарами на концах и небольшим искровым промежутком посредине (рис. 17.2). Электроемкость вибратора определяется емкостями шаров, а индуктивность – индуктивностями обеих половин стержня. Источником возбуждения электромагнитных колебаний в ибраторе является индукционная катушка (ИК). Провода от вторичной обмотки ИК подключены к искровому промежутку. Когда переменное напряжение во вторичной
Рис 17.2 обмотке катушки достигает значения пробивного напряжения, в искровом промежутке проскакивает искра, в вибраторе возникают электромагнитные колебания высокой частоты, сопровождающиеся излучением электромагнитных волн по всему пространству, окружающему вибратор. Поэтому вибратор Герца является открытым колебательным контуром. При каждом периоде колебаний вибратора от него излучается группа замкнутых линий напряженности электрического и магнитного полей.
Для регистрации (приема) электромагнитных волн используется аналогичный вибратор - резонатор, в котором под действием электромагнитного поля волны возникают вынужденные электромагнитные колебания. Если частоты колебаний в вибраторе и резонаторе одинаковые, то наступает электрический резонанс, при котором вынужденные колебания в резонаторе обнаруживаются либо по проскакиванию
Рис. 17.3 искры в его искровом промежутке, либо по свечению небольшой газоразрядной трубки, подключенной к искровому промежутку (рис 17.3). С помощью подобной системы Герц провел серию опытов, в которых обнаружил существование электромагнитных волн, их поперечность и наблюдал явление интерференции электромагнитных волн. Герц установил, что электромагнитные волны распространяются со скоростью света, подчиняются законам видимого света.
Распространение электромагнитных волн связано с переносом энергии электромагнитного поля волны. Энергия переносится в направлении распространения волны, то есть в направлении вектора скорости 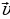 . Объемная плотность энергии электромагнитного поля волны
. Объемная плотность энергии электромагнитного поля волны
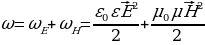 (17.12)
(17.12)
Средней мощностью излучения (потоком излучения)  называется средняя энергия, которая за единицу времени испускается источником электромагнитных волн по всем направлениям
называется средняя энергия, которая за единицу времени испускается источником электромагнитных волн по всем направлениям
 =
=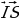 (17.13), где
(17.13), где 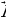 - интенсивность электромагнитной волны, которая определяется аналогично интенсивности упругой волны и выражается формулой
- интенсивность электромагнитной волны, которая определяется аналогично интенсивности упругой волны и выражается формулой
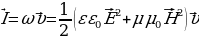 (17.14)
(17.14)
Применительно к электромагнитной волне вектор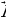 называют вектором Умова-Пойнтинга.
называют вектором Умова-Пойнтинга.
Нестационарное электрическое поле (или магнитное) является источником электромагнитного излучения.
Радиосвязью называется передача информации с помощью радиоволн -электромагнитных волн, частоты которых охватывают широкий диапазон: от 3-104 до 3-1011 Гц. Радиоволны делятся на группы (см. таблицу 1). Таблица 1. Классификация радиоволн.
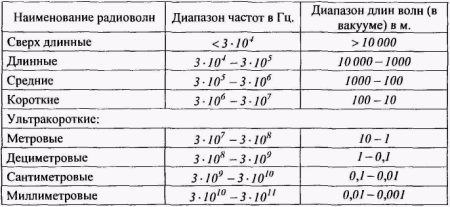
В 1896г. А.С.Попов впервые осуществил передачу телеграфных сигналов с помощью свободно распространяющихся электромагнитных волн, что явилось началом радиосвязи.
С помощью радиовещания осуществляется передача речи и музыки. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией называется изменение параметров электромагнитной волны (амплитуды, частоты, начальной фазы) частотами, значительно меньшими частоты самой электромагнитной волны. Частота исходной (высокой немодулированной) волны называется несущей частотой, а частота изменения параметров волны при модуляции - частотой модуляции. Схема радиопередатчика изображена на рис.17.4а.

Рис 17.4
Генератор незатухающих колебаний (задающий генератор) вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон и преобразовываются в электрические колебания. В модуляторе незатухающие синусоидальные колебания преобразовываются в модулированные колебания. После усиления, модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны.
Приемное устройство (радиоприемник) схематически изображено на рис. 17.4 б). Электромагнитные волны поступают в антенну приемника и вызывают электромагнитные колебания в резонирующем контуре (РК). Слабые колебания высокой частоты поступают в усилитель, а затем в детектор -проводник с односторонней проводимостью. В детекторе происходит процесс демодуляции - выделения низкочастотной составляющей колебаний из колебаний с несущей частотой. Из детектированных колебаний выделяется низкочастотная (звуковая) составляющая, которая вновь усиливается и передается на воспроизводящее устройство (динамик, телефон и т.д.)
Резонирующий контур приемника состоит из катушки и конденсатора. Для высококачественного воспроизведения в приемнике сигналов, передаваемых радиостанций, необходимо, чтобы частота модуляции была в 5-10 раз меньше несущей частоты. Для передачи речи и музыки модуляция осуществляется со звуковыми частотами, обычно не превосходящими (10-13)-103 Гц. Для радиовещания можно использовать все диапазоны радиоволн, начиная с длинных.
Схема телевидения в основном совпадает со схемой радиовещания. В передатчике колебания несущей частоты модулируются не только звуковым сигналом, но и предварительно усиленными сигналами изображения, поступающими от передающих трубок. В объем модуляции входят также сигналы для синхронизации развертки электронного пучка в электронно-лучевой трубке - иконоскопе, на экране которого возникает изображение. В телевизионном приемнике высокочастотный сигнал разделяется на три: сигнал изображения, звуковое сопровождение, сигнал управления. Сигналы управления синхронизируют работу генераторов, осуществляющих развертку электронного луча по горизонтали - вдоль строк и перебрасывание его с одной строки на другую. Всего за 1/25 секунды электронный пучок записывает 625 строк, составляющих один кадр. Усиленный сигнал изображения подается на управляющий электрод электронной пушки. Телевизионный сигнал несет большой объем информации и занимает полосу частот порядка 4-5 МГц (в радиовещательном приемнике - около 10 кГц). В качестве несущих частот электромагнитных волн используются высокие частоты - от 50 МГц до 900 МГц (что соответствует длинам волн от 6 м до 30 см).
Радиолокацией называется обнаружение и определение местонахождения различных объектов с помощью радиоволн. Радиолокация основана на явлении рассеяния и отражения радиоволн телами. Радиолокатор (радар) представляет собой комбинацию ультракоротковолнового радиопередатчика и радиоприемника, имеющих общую приемно-передающую антенну, которая создает остронаправленное излучение (радиолуч). Излучение осуществляется короткими импульсами с продолжительностью около 10-6 с.
В радиолокационной астрономии методы радиолокации используются для уточнения движения планет Солнечной системы и их спутников, искусственных спутников Земли, космических кораблей и т.д. Для приема и изучения радиоизлучения космических объектов применяются специальные радиотелескопы, чувствительность которых, благодаря большим площадям антенн очень высока. С помощью радиотелескопов изучаются планеты Солнечной системы, солнечная активность и т.д.
Исследованиями многих ученых была установлена электромагнитная природа различных видов излучения, которые отличаются друг от друга частотой и условиями возникновения.
Радиоволны характеризуются длиной волны от 10 км до долей миллиметра. Регистрируются они с помощью колебательного контура. При исследованиях в химии и биологии используется ультракоротковолновая (микроволновая) область - от 1 м до долей миллиметра.
Инфракрасные лучи (ИК-лучи) имеют длину волны от 1 мм до 760 им. Различают две области ИК-лучей: ближнюю (760 - 5000 нм) и дальнюю (5000 нм - 1 мм). Испускаются ИК-лучи нагретыми телами и регистрируются с помощью тепловых приемников - термопар и болометров, фотоэлементов и фотосопротивлений, специальных фотопластинок.
Видимый свет — электромагнитные волны, воспринимаемые глазом. Длины волн видимого света лежат в диапазоне от 380 до 760 нм. Излучение в узком интервале длин волн ∆λ глаз воспринимает как одноцветное, а сложное излучение, содержащее все длины волн,— как белый свет.
Ультрафиолетовые лучи (УФ-лучи) имеют диапазон длин волн от 380 до 1 нм. Они содержатся в составе излучения Солнца, накаленных твердых тел и электрического газового разряда. Различают две области УФ-излучения: ближнюю (380 - 180 нм) и дальнюю (180 - 10 нм). При λ 180 нм УФ-лучи сильно поглощаются всеми веществами, включая воздух. Регистрируются УФ-лучи с помощью фотопластинок, фотоэлементов, фотосопротивлений. Они вызывают ионизацию газов, фотохимические реакции, люминесценцию многих веществ и проявляют биологическую активность. Сквозь обычное стекло УФ-лучи не проходят.
Рентгеновские лучи (R-лучи) имеют диапазон длин волн от 10 до 10-2 нм. В лабораториях эти лучи получают с помощью рентгеновских трубок, а регистрируются они фотографическим, ионизационным и люминесцентным методами. Рентгеновские лучи хорошо проникают сквозь многие вещества, но сильно поглощаются атомами тяжелых элементов. Они производят ионизацию газов и оказывают сильное биологическое действие.
Гамма-лучи (γ-лучи) имеют длину волны меньше 0,1 нм. Испускаются γ-лучи радиоактивными ядрами атомов. Это самое коротковолновое электромагнитное излучение. Оно обладает большой проникающей способностью и биологически очень активно. Обнаруживаются γ-лучи по вызываемой ими ионизации атомов веществ, сквозь которые они проходят. Границы диапазонов длин волн условны; эти диапазоны частично перекрываются. Совокупность диапазонов ИК, УФ и видимого излучений образует оптический диапазон.







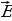 , которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами провода, несущего ток, должна существовать разность потенциалов U (напряжение или падение напряжения). Сила тока является функцией разности потенциалов
, которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами провода, несущего ток, должна существовать разность потенциалов U (напряжение или падение напряжения). Сила тока является функцией разности потенциалов 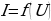 .
.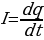 (5.1)
(5.1)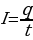 I=Const. (5.2)
I=Const. (5.2)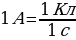 ; 1мА = 10-3 А; 1мкА = 10-6 А.
; 1мА = 10-3 А; 1мкА = 10-6 А.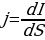 (5.5)
(5.5)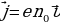 (5.6)
(5.6) направлено антипараллельно вектору скорости электронов).
направлено антипараллельно вектору скорости электронов).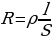 , (5.7)
, (5.7)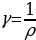 , (5.8)
, (5.8)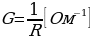 (5.9)
(5.9)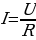 (5.10)
(5.10)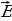 в некоторой точке проводника. В окрестности этой точки
в некоторой точке проводника. В окрестности этой точки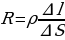 , подставив эти значения в закон Ома для участка цепи
, подставив эти значения в закон Ома для участка цепи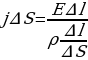 ; или
; или 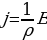 , так как направления векторов
, так как направления векторов 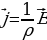 (5.11)
(5.11) (5.12)
(5.12)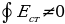 (5.13)
(5.13)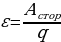 (5.14)
(5.14)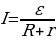 (5.15)
(5.15)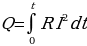 (5.23)
(5.23)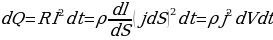 (5.24)
(5.24)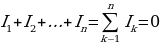 , (5.26)
, (5.26)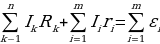 (5.27)
(5.27)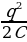 (где q
(где q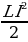 . Когда конденсатор полностью разрядится, ток в катушке и связанная с ним энергия магнитного поля достигнут максимума. Ток будет некоторое время поддерживаться за счет ЭДС самоиндукции, пока конденсатор не перезарядится. Энергия магнитного поля катушки преобразуется в энергию электрического поля перезаряженного конденсатора. Конденсатор снова начнет разряжаться, и явления повторятся в обратной последовательности. За время Т в контуре восстановится исходное состояние. Возникают периодические электрические колебания, сопровождающиеся превращением электрической энергии в магнитную и обратно.
. Когда конденсатор полностью разрядится, ток в катушке и связанная с ним энергия магнитного поля достигнут максимума. Ток будет некоторое время поддерживаться за счет ЭДС самоиндукции, пока конденсатор не перезарядится. Энергия магнитного поля катушки преобразуется в энергию электрического поля перезаряженного конденсатора. Конденсатор снова начнет разряжаться, и явления повторятся в обратной последовательности. За время Т в контуре восстановится исходное состояние. Возникают периодические электрические колебания, сопровождающиеся превращением электрической энергии в магнитную и обратно.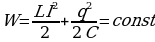 . (15.1)
. (15.1)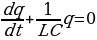 (15.2)
(15.2)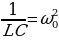 , приходим к следующей записи:
, приходим к следующей записи: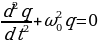 (15.3)
(15.3)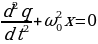 (15.5)
(15.5)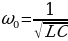 , а период этих колебаний определяется формулой Томсона:
, а период этих колебаний определяется формулой Томсона: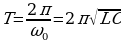 (15.6)
(15.6)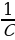 :
: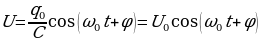 . (15.7)
. (15.7)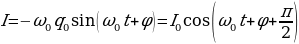 . (15.8)
. (15.8)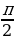 .
.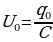 ,
, 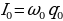 . Используя выражение
. Используя выражение 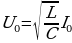 . (15.9)
. (15.9)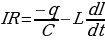 . (15.10)
. (15.10)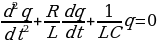 . (15.11)
. (15.11)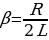 (β коэффициент затухания), получим выражение (15.11) в виде:
(β коэффициент затухания), получим выражение (15.11) в виде: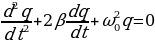 (15.12)
(15.12)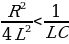 , решение уравнения (15.12) имеет вид:
, решение уравнения (15.12) имеет вид: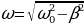 . Подставив значения
. Подставив значения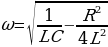 . (15.14)
. (15.14)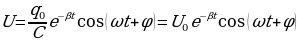 . (15.15)
. (15.15)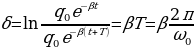 . (15.18)
. (15.18)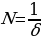 определяет число периодов, за которое амплитуда колебаний убывает в е раз.
определяет число периодов, за которое амплитуда колебаний убывает в е раз.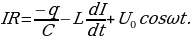 (15.20)
(15.20)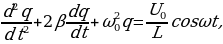 (15.21)
(15.21)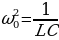 ,
, 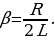
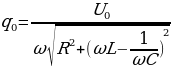 (15.23)
(15.23) 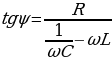 . (15.24)
. (15.24)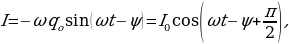 или
или 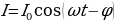 , (15.25)
, (15.25)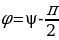 есть сдвиг по фазе между током и напряжением, тогда
есть сдвиг по фазе между током и напряжением, тогда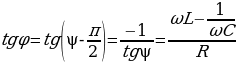 (15.26)
(15.26)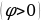 в том случае, когда
в том случае, когда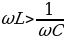 , и опережает напряжение
, и опережает напряжение 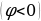 при условии, что
при условии, что 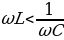 .
.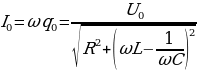 (15.27)
(15.27)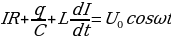 (15.28)
(15.28)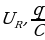 - напряжение на конденсаторе
- напряжение на конденсаторе 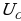 , выражение
, выражение 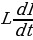 определяет напряжение на индуктивности
определяет напряжение на индуктивности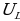 . С учетом этого можно записать
. С учетом этого можно записать 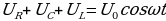 (15.29)
(15.29)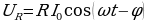 (15 30)
(15 30)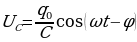 (15.31)
(15.31)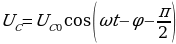 (15.32)
(15.32)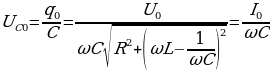
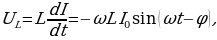 (15.33)
(15.33) 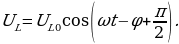 (15.34)
(15.34) 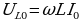
 из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.
из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора. свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.
свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.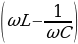 обращается в нуль в законе Ома
обращается в нуль в законе Ома 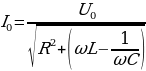 , сила тока I при этом достигает максимального значения
, сила тока I при этом достигает максимального значения 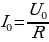 , контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ.
, контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ.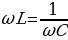 , сдвиг фаз φ становится равным нулю и,
, сдвиг фаз φ становится равным нулю и,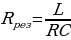 . При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей.
. При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей. , то
, то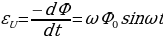 (14.2), так как ωФ0 = ε0, то ε = ε0sinωt .
(14.2), так как ωФ0 = ε0, то ε = ε0sinωt .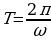 , а амплитудное значение ЭДС ε0 пропорционально скорости вращения ω. Рассмотренный принцип лежит в основе
, а амплитудное значение ЭДС ε0 пропорционально скорости вращения ω. Рассмотренный принцип лежит в основе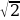 )
)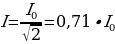 (14.3) Аналогично
(14.3) Аналогично 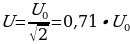 (14.4)
(14.4)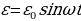 - ЭДС изменяется по синусоидальному закону, ток I- так же
- ЭДС изменяется по синусоидальному закону, ток I- так же 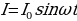 ,L = 0,С = 0.
,L = 0,С = 0.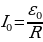
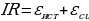 , т.к.
, т.к. 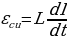 то
то 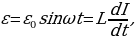
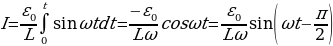
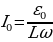
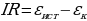 (т.к.
(т.к. 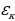 направлено противоположно
направлено противоположно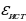 )
) 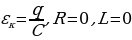 то
то 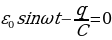 т.к.
т.к. 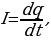 то
то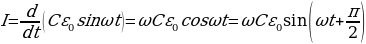 I опережает ε на
I опережает ε на 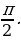
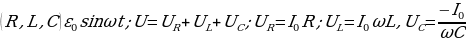
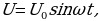 сила тока изменяется по закону
сила тока изменяется по закону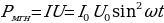 (14.8)
(14.8)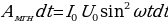 (14.9)
(14.9)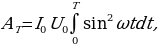 (14.10) но
(14.10) но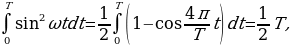 поэтому
поэтому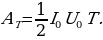 (14.11) Средняя мощность:
(14.11) Средняя мощность: 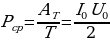 (14.12)
(14.12)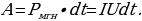
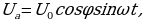 колеблющуюся в фазе с током, и реактивную
колеблющуюся в фазе с током, и реактивную 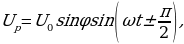 смещенную по фазе относительно тока на
смещенную по фазе относительно тока на 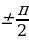 . При вычислении работы за полный период Т получим тоже два слагаемых. Одно из них, обусловленное реактивной составляющей напряжения UP, равно нулю, так как
. При вычислении работы за полный период Т получим тоже два слагаемых. Одно из них, обусловленное реактивной составляющей напряжения UP, равно нулю, так как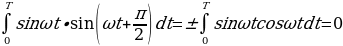 (14.13)
(14.13)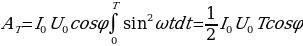 (14.14) Средняя мощность
(14.14) Средняя мощность 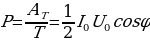 (14.15)
(14.15)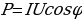 (14.16) т.е. выделяемая в цепи мощность зависит не только от силы тока и напряжения, но еще и от сдвига фаз между напряжением и током. Косинус угла
(14.16) т.е. выделяемая в цепи мощность зависит не только от силы тока и напряжения, но еще и от сдвига фаз между напряжением и током. Косинус угла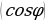 в электротехнике называют коэффициентом мощности.
в электротехнике называют коэффициентом мощности.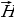 расположены во взаимно перпендикулярных плоскостях. Распространяющееся в пространстве периодически меняющееся электромагнитное поле образует электромагнитную волну. Из уравнений Д.К. Максвелла следует, что для плоской монохроматической электромагнитной волны, распространяющейся вдоль оси r имеем:
расположены во взаимно перпендикулярных плоскостях. Распространяющееся в пространстве периодически меняющееся электромагнитное поле образует электромагнитную волну. Из уравнений Д.К. Максвелла следует, что для плоской монохроматической электромагнитной волны, распространяющейся вдоль оси r имеем: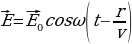 ,
, 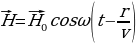 , где
, где 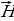 мгновенные, а
мгновенные, а 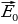 и
и 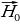 – амплитудные значения напряженности электрического и магнитного полей, ω – циклическая частота колебаний, υ – фазовая скорость волны. Векторы
– амплитудные значения напряженности электрического и магнитного полей, ω – циклическая частота колебаний, υ – фазовая скорость волны. Векторы 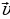 , указывающему направление распространения волны (рис. 17.1)
, указывающему направление распространения волны (рис. 17.1)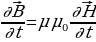 ,
, 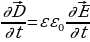 ,
, 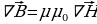 ,
, 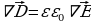
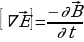 (17.1),
(17.1), 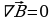 (17.2),
(17.2), 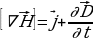 (17.3),
(17.3),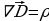 (17.4) можно записать следующим образом
(17.4) можно записать следующим образом 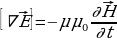 (17.5),
(17.5), 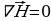 (17.6),
(17.6), 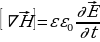 (17.7),
(17.7), 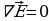 (17.8)
(17.8)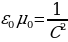 раскрыв оператор Лапласа, получим
раскрыв оператор Лапласа, получим 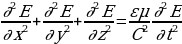 (17.9)
(17.9)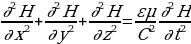 (17.10)
(17.10)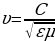 (17.11)
(17.11)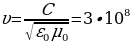 (м/с)
(м/с)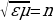 называется абсолютным показателем преломления среды и показывает, во сколько раз скорость электромагнитных волн в вакууме больше их скорости в данной среде.
называется абсолютным показателем преломления среды и показывает, во сколько раз скорость электромагнитных волн в вакууме больше их скорости в данной среде.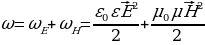 (17.12)
(17.12)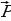 называется средняя энергия, которая за единицу времени испускается источником электромагнитных волн по всем направлениям
называется средняя энергия, которая за единицу времени испускается источником электромагнитных волн по всем направлениям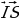 (17.13), где
(17.13), где 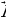 - интенсивность электромагнитной волны, которая определяется аналогично интенсивности упругой волны и выражается формулой
- интенсивность электромагнитной волны, которая определяется аналогично интенсивности упругой волны и выражается формулой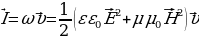 (17.14)
(17.14)





















