Электромагнитные колебания и волны

Электромагнитные колебания и волны

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

• Электромагнитные колебания - взаимосвязанные колебания электрического и магнитного полей.

• Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

• Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

• Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

• Вынужденные электромагнитные колебания - незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

• Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

• Электрические колебания - частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

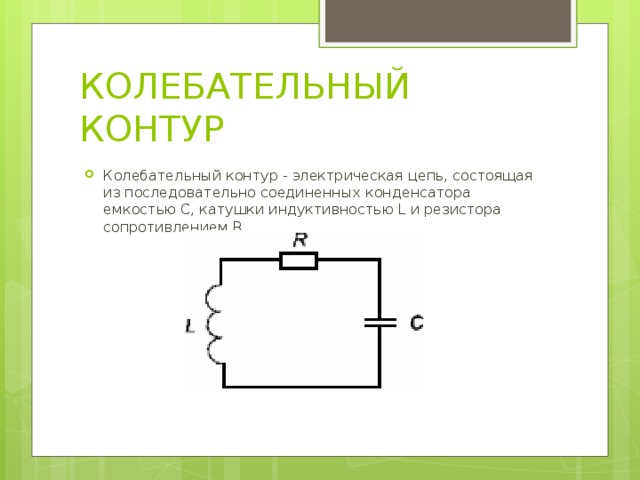
КОЛЕБАТЕЛЬНЫЙ КОНТУР

• Колебательный контур - электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

• Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

• Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

• величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

• Можно показать, что уравнение свободных колебаний для заряда q = q(t) конденсатора в контуре имеет вид

где q" - вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

• Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ0, стоящая под знаком синуса или косинуса, является фазой колебания.

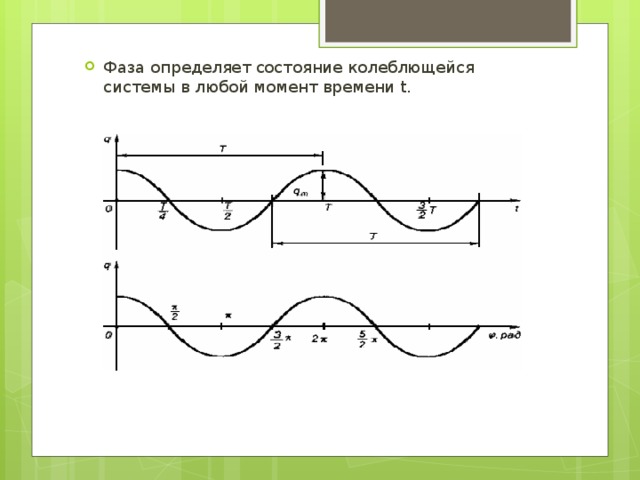
• Фаза определяет состояние колеблющейся системы в любой момент времени t.

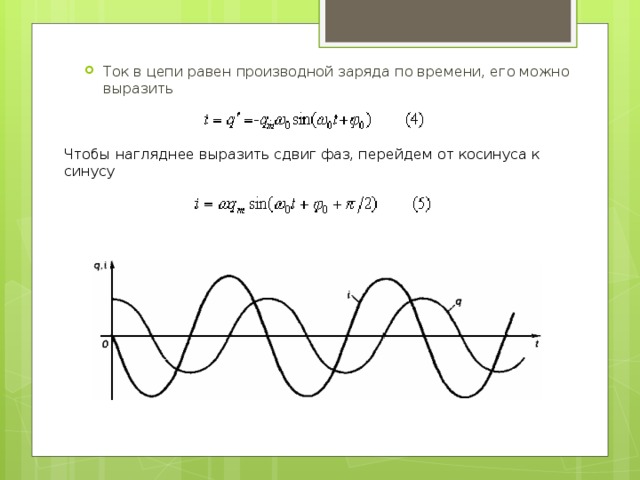
• Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

• 1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

Где - угол между нормалью к рамке и вектором магнитной индукции .

• По закону электромагнитной индукции Фарадея ЭДС индукции равна

где - скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где - амплитудное значение ЭДС индукции.

• 2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника .

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

• Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность - отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

• Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения