Факультативный курс по математике «Графы» для 5-6 классов

Муниципальное бюджетное общеобразовательное учреждение

Средняя общеобразовательная школа №2

города Азова Ростовской области

Факультативный курс по математике

«Графы» для 5-6 классов

подготовила

учитель математики

Данькова Валентина Николаевна

г. Азов

Тема графов очень интересна при изучении, что позволяет привлечь школьников к активной познавательной деятельности. Графы, как никакая другая модель, позволяет изучать свойства отношений в «чистом виде», а графическое представление  решения логических задач  делает этот процесс более наглядным. С помощью графов решать задачи очень удобно, интересно, увлекательно, можно рассмотреть несколько вариантов решения одной и той же задачи и выбрать наиболее легкое, удобное, красивое, интересное решение задачи.

Начальные сведения о графах как геометрических схемах, состоящих из точек (вершин) и соединяющих их линий (ребер), достаточно просты, а работа с ними вызывает у детей большой интерес.

В школьном курсе математики теория графов не рассматривается, но в учебниках начальных классов и основной школы, можно встретить задачи, которые намного проще решить с помощью графов, нежели другими способами. Олимпиадные задачи и некоторые задачи ЕГЭ тоже наполнены заданиями, которые легче решить, применяя графический способ. Но что мешает учителю включить в факультативный курс теорию графов и показать, как с ее помощью можно быстро решать «сложные» задачи. Тем более, что некоторый теоретический материал доступен для понимания детей уже даже начальной школы.

Задачи по теории графов можно предлагать не только детям, посещающим факультативы, но и на некоторых уроках математики для развития логического мышления. Но вводить такие задачи нужно постепенно, начиная с элементарных заданий, даже почти с устных, и постепенно повышать уровень их сложности. Конечно, для неподготовленных детей, такие задачи сначала вызовут затруднения в решении, и поиск решения может занимать достаточно долгое время. Поэтому на первых этапах задачи по графам лучше всего задавать, как дополнительное домашнее задание, но не обязательное для всех учащихся. При первом «домашнем» знакомстве с такими упражнениями учителю не обязательно сообщать детям, что при их решении применяется теория графов. Новый неизвестный термин может психологически оттолкнуть детей от поиска решения: «я не решу, ведь мы этого не проходили», хотя и решение может быть совсем легким, элементарным. Лишь только когда дети почувствуют силу при решении задач, можно сказать детям, что эти задания выделяют в особый раздел математики – топологию, теорию графов. Особенно важно, на этом этапе, похвалить тех детей, которые решали или пытались решать задачи, и сказать всему классу, что в их силах решать даже некоторые задачи по неизвестной теме. В дальнейшем можно раз в неделю уделять по 5 минут в конце уроке для дальнейшего изучения теории графов. Но более детальное рассмотрение темы, всё же, надо вынести на факультативный курс.

Для школьника не обязательно давать строгое определение графа, как математического объекта. Им вполне достаточно будет сформулировать несколько определений и теорем и показать, как они работают при решении задач.

Итак, сформулируем основные определения и теоремы на которых можно построить факультативный курс по графам.

Граф – это набор точек, некоторые из которых соединены линиями.

Особо важно обратить внимание детей в определении на том, что могут соединяться не все точки друг с другом и соединяются не обязательно отрезками, а произвольными линиями-дугами. Далее целесообразно подкрепить новое определение примерами – наглядными рисунками.

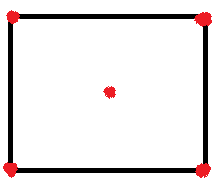
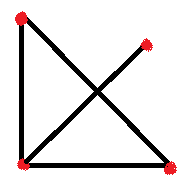
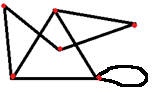
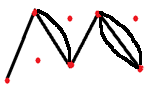
рис.1 рис.2 рис.3 рис.4 рис.5

На вышеприведенных примерах очень удобно ввести следующие понятия: вершины (точки) и ребра (линии, соединяющие вершины) графа и закрепить эти понятия на примерах. Четкого, строгого обозначения вершин не существует, обозначают из контекста задачи: или буквами (русскими, латинскими) или цифрами. Причем нужно особо подчеркнуть, что бывают графы, состоящие только из одних вершин (рис.5), что две вершины могут быть соединены несколькими ребрами одновременно (рис.4) и что ребро может «выходить и заходить» в одну и ту же вершину (рис.3) – такое ребро называют петлей.

Можно рассказать детям, что графы используются не только в математике и привести примеры «нематематических графов». Так, например, люди часто пользуются графами, не догадываясь об этом, когда изображают различные объекты: населенные пункты, карты городов, схемы электроприборов, атомы. Схема метро это тоже граф: вершины конечные станции и станции пересадок, ребра – пути, соединяющие эти станции.  Дворянство тоже применяло графы для создания генеалогического дерева. В них вершины – это члены рода, а связывающие их линии - отношения родственности, ведущие от родителей к детям. Ниже приведен фрагмент родословной А.С. Пушкина.

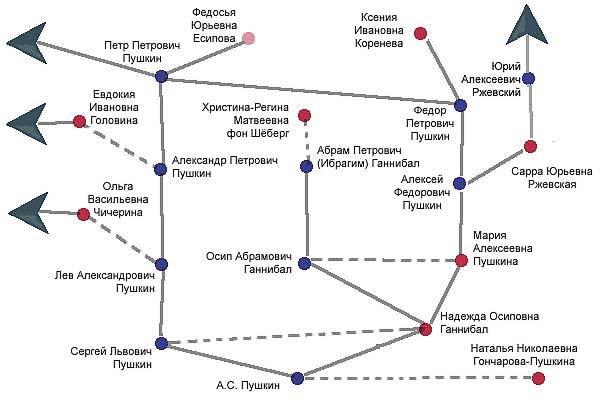
Графы бывают конечные (число его ребер конечно) и бесконечные (число его ребер бесконечно). В начальной школе и 5-6 классах задачи на бесконечные графы не предлагают, но для детей постарше можно привести пример такого графа. Например, когда каждой вершине графа соответствует натуральное число, т.е. вершины графа нумеруются числами 1, 2, 3… Но так как ряд натуральных чисел бесконечен, то и граф тоже бесконечный. Конечно, полностью изобразить бесконечный граф нельзя, но можно изобразить его частично.

рис.6

Степень вершины – число ребер выходящих из вершины графа. Если ребро является петлей, то его считают дважды. Закрепляем определение примерами (см. рис.1-5).

Иногда степень вершины записывают в виде таблицы, а иногда пишут рядом с самой вершиной. Важно подчеркнуть, что одно и тоже ребро считается дважды (один раз – для одной вершины, второй – для другой), так как оно соединяет две вершины.

Вершины бывают четные (степень вершины четна) и нечетные (степень вершины нечетна).

Первые задания, которые можно предлагать по теме графы, связаны как раз с этими понятиями: построить граф, определить по рисунку, сколько вершин, ребер у граф, какова степень вершины графа, посчитать сколько четных и нечетных вершин и тому подобные задания. Такие задания можно предлагать и в начальной школе, так как они вполне доступны детям 3-4 классов.

Задание: По рисунку определить: сколько вершин, ребер у графа и какова степень каждой вершины графа?

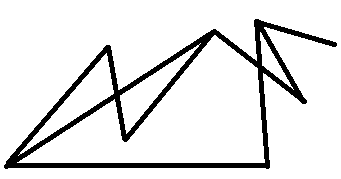
рис.7

Решение: Сначала посчитаем количество вершин. Для наглядности на первых порах их можно выделить другим цветом – 8 вершин (рис.8). Для подсчета ребер удобно посчитанное ребро выделять черточкой, чтобы не посчитать его дважды – 9 ребер (рис.9)

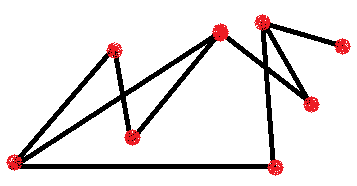
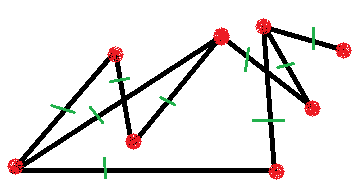
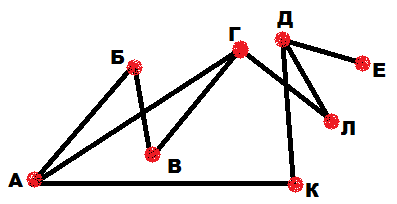
рис.8 рис.9 рис.10

Для определения степени вершины графа лучше все вершины обозначить буквами (рис.10), а потом результаты записать в таблицу.

Первое свойство, которое вводим детям без доказательства: «Число нечетных вершин графа – четно». И в дальнейшем, все свойства и теоремы даются без строгого доказательства. Закрепление данного свойства происходит так же на решении задач.

Задание: Построить граф у которого вершины имеют следующие степени:

а) А – 7, Б – 3, С – 1; б) А – 5, Б – 1, С – 4.

Решение: При решении задач на построение графов, надо объяснить детям, что сначала необходимо проверить, возможно ли вообще построение заданного графа. Для этого учащиеся должны применить первое свойство. Сколько бы дети не пытались построить граф а), у них ничего не получится. Построение графа а) невозможно, так как все его вершины нечетные, и число их нечетно. А вот граф б) построить можно, так как у него две нечетных вершины. Причем у детей могут получаться различные по конфигурации графы (рис.11-13). Именно на таких заданиях и закрепляется, что число нечетных вершин графа – четно.

Поучительная сторона этих задач состоит в исследовании, возможно или нет решение данной задачи, прежде чем приниматься за само решение.

Обратите внимание детей, что построение графа следует начинать с изображения всех его вершин, и лишь потом соединять их ребрами. Причем лучше всего начинать соединять ребрами вершины с наименьшей и наибольшей степенью.

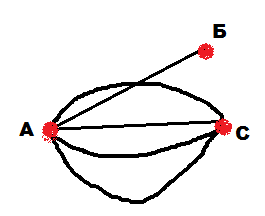
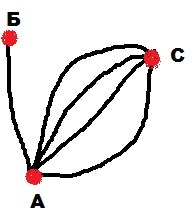
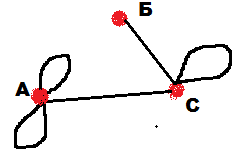
рис.11 рис.12 рис.13

Далее лучше всего дать задания такого плана: «без построения графа, определить число ребер графа».

Свойство 2: Для того чтобы найти количество ребер в графе, надо просуммировать степени вершин и результат разделить пополам.

Задание: Даны степени вершин графа: А – 2, Б – 5, С – 1, Д – 4. Без построения графа, определить число ребер графа.

Решение: Первое, что должны проверить дети: возможно ли построение такого графа. Чтобы проверить это, надо сосчитать число нечетных вершин – их должно быть четно. По условию задачи 2 нечетных вершины Б и С, значит построение возможно. Теперь можно ответить на вопрос задачи, используя второе свойство: (2+5+1+4):2=6.

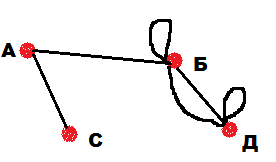
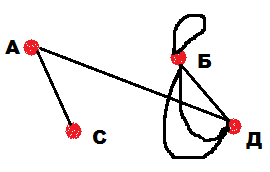
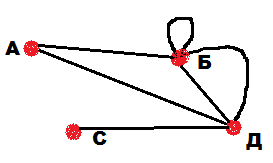
После решения задачи можно предложить детям построить этот граф и проверить решение. Причем рисунки могут получиться совершенно разные, в зависимости от того, какие вершины будут соединены (рис.14-16). Самое главное, чтобы степени вершин соответствовали условию задачи. Эти задания не сложные и доступны учащимся 5 классов. рис.14 рис.15 рис.16 Связный граф – граф, у которого любые две его вершины можно соединить непрерывной последовательностью ребер. Другими словами: из любой вершины можно пройти в другую вершину по ребрам (рис.17-18). Несвязный граф – граф, который состоит из нескольких частей, каждая из которых или связный граф, или отдельные вершины (рис.19). 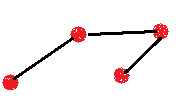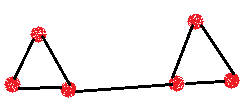рис.17 рис.18 рис.19 Предложенный выше теоретический материал по графам вполне доступен детям 5-6 классов. Рассмотрим ниже основные задачи, опираясь на которые можно построить факультативный курс по математике. Такие задачи, как правило, встречаются в математических олимпиадах или в разделе задач со звездочками.

1. Десять человек приветствовали друг друга рукопожатиями. Пять человек сделали по семь рукопожатий, трое – по пять, двое – по четыре. Сколько всего было сделано рукопожатий?

Решение: Вначале надо разобраться с детьми, правильно ли они понимают понятие рукопожатие на языке графов. Одно рукопожатие – это две вершины соединены одним ребром. То есть, два человека и у них одно рукопожатие на двоих. Данную задачу можно переформулировать на язык графов следующим образом: дано 10 вершин, известны степени каждой вершины и нужно узнать, сколько ребер в этом графе. Чтобы узнать количество ребер в графе надо сложить степени каждой вершины и разделить пополам – применить второе свойство . Так как пять человек сделали по семь рукопожатий, то это значит, что из пяти вершин выходят по семь ребер, а всего ребер: 5+5+5+5+5+5+5=5*7. Аналогично рассуждаем и с остальными вершинами, получаем: (5*7+3*5+2*4)/2=(35+15+8)/2=58/2=29

1. Можно ли организовать футбольный турнир девяти команд так, чтобы каждая команда провела по четыре встречи?

Решение: Переформулируем задачу на язык графов: можно ли построить такой граф, у которого 9 вершин и степень каждой вершины равна 4. По свойству два, найдем число ребер и если оно будет целым числом, то такой турнир можно организовать, в противном случае – нельзя. (9*4)/2=18. Да, можно и будет сыграно 18 игр.

1. Можно ли 15 телефонов соединить между собой так, чтобы каждый из них был связан ровно с 11 другими?

Решение: Переформулируем задачу на язык графов: можно ли построить такой граф, у которого 15 вершин и степень каждой вершины равна 11. Применим второе свойство: 15*11/2=82,5. Получили не натуральное число, значит нельзя соединить телефоны.

1. В государстве 100 городов, из каждого выходит 4 дороги. Сколько всего дорог в государстве?

Решение: Одна дорога соединяет два города, т.е. две вершины соединены одним ребром. Применим второе свойство: 100*4/2=200.

1. Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

Решение: Решим задачу, составив уравнение: х*3/2=100, где х – число городов в государстве. Х*3=200, х=66,(6) – число не натуральное, значит в таком государстве не может быть ровно 100 дорог. После отработки выше изложенного материала на задачах можно приступать к дальнейшему изучению теоретического материала по теме графы. Цикл – замкнутый путь в графе. Графы бывают с циклом (рис.20 цикл выделен голубым цветом) и без цикла (рис.21). 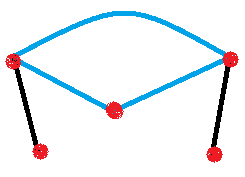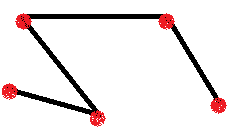рис.20 рис.21 рис.22 Дерево – связный граф, не имеющий циклов (рис.22). Перед введением этого определения обязательно надо повторить понятие связный граф. Далее предлагаем задания следующего типа: Задание: Среди предложенных графов (рис.23-26) найти графы-деревья и графы с циклом. Укажите, сколько вершин входит в цикл? 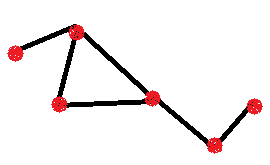рис.23 рис.24 рис.25 рис.26 Решение: Графы-деревья изображены на рис.24 и рис.25; графы с циклом – рис.23 (цикл состоит из 3 вершин) и рис. 26 (цикл состоит из 4 вершин). Далее вводим еще одно важное свойство, которое очень часто применяется при решении логических задач. Свойство 3: Если граф связный и нечетных вершин у него 0 или 2, то его можно обойти, пройдя по каждому ребру только один. По-другому можно переформулировать это свойство так: Если граф связный и нечетных вершин у него 0 или 2, то его можно начертить, не отрывая карандаш от бумаги и не проходя по любому ребру дважды. Если можно начертить граф, не отрывая карандаш от бумаги и не проходя по любому ребру дважды, то такой граф называют уникурсальным или Эйлеровым графом. Как правило, задания на это свойство вызывают у детей наибольший интерес. Задание: Из предложенных графов (рис.27- 33) найти те, которые можно изобразить одним росчерком (т.е. не отрывая карандаш от бумаги и не проходя по любому ребру дважды) и нарисовать их в тетради. рис.27 рис.28 рис.29 рис.30 рис.31 рис.32 рис.33 Решение: Для решения этого задания необходимо посчитать степени всех вершин, определить нечетные вершины и посчитать их количество. Если их 2 или 0, то граф построить можно в противном случае – нет. Перед тем, как изображать графы в тетради необходимо рассказать детям, что для более быстрого и правильного способа изображения графов надо знать: если граф имеет две нечетных вершины, то его изображение надо начинать из одной нечетной вершины, а заканчивать – в другой. Если же все вершины графа четные, то начало и конец графа совпадают. Графы, изображенные на рис.27, 28, 33 нельзя нарисовать, а остальные можно. В качестве домашнего задания можно предложить детям проанализировать печатные буквы русского алфавита и найти среди них те, которые можно написать одним росчерком, а какие нельзя и объяснить почему? Если применить немного фантазии и воображения, то одним росчерком можно изобразить много необычных рисунков (рис.34-36). рис.34 рис.35 рис.36 Для отработки понятия Эйлеров граф полезно дать задание следующего типа: Задание: Достроить графы до Эйлеровых (рис.37-39) рис. 37 рис. 38 рис.39 Решение: Чтобы решить это задание, надо сначало посчитать степень каждой вершины и дополнить ребрами граф так, чтобы стало две нечетных вершины или ни одной. На рис. 40-42 представлен один из вариантов решения. рис.40 рис.41 рис.42 Детям постарше, начиная с 7 класса, можно ввести понятия ориентированный, неориентированный графы и мультиграф. Если ребро соединяет вершину А с вершиной В и пара (А,В) считается упорядоченной, то это ребро называют ориентированным, вершину А – его началом, вершину В – его концом, а само ребро изображают в виде стрелки. Если же эта пар считается неупорядоченной, то ребро называют неориентированным, а обе вершины – его концами. Граф с ориентированными ребрами называется ориентированный. Граф с неориентированными ребрами называется неориентированный. Например, только из города А в город В едет автобус №1, а из города Д в город С и обратно едет автобус №2. Изображением маршрута автобуса №1 будет ориентированный граф, вершина А будет его началом, а вершина В будет его концом (рис. 43). Изображением маршрута автобуса №2 будет неориентированный граф, и вершины С и Д будут называться его концами (рис.44). рис.43 рис.44 Кратные ребра – это разные ребра, но имеющие одинаковые начала и концы. Граф с кратными ребрами называют мультиграфом (рис.45). рис.45 В 5-6 классах, как правило, решаются задачи, в которых используются обыкновенные графы, то есть неориентированные графы без петель и без кратных ребер.

1. Встретились три друга – Белов, Серов и Чернов. Чернов сказал другу, одетому в серый костюм: «На одном из нас белый костюм, на другом – серый и на третьем – черный, но на каждом костюм цвета, не соответствующего фамилии». Какой цвет костюма у каждого?

Решение: Начнем решать задачу с построения графа. Первые три вершины будут обозначать фамилии трех друзей. Вторые три вершины – цвета их костюмов. Причем, для большей наглядности, вторая тройка вершин должна находиться справа от первой тройки. Наша задача построить три ребра, то есть соединить фамилию с цветом костюма. Так как цвет костюма не соответствует фамилии, то пунктиром покажем, куда нельзя проводить ребра. Далее анализируем условие задачи: «Чернов сказал другу, одетому в серый костюм», значит на Чернове не серый костюм. Покажем это условие так же пунктиром. Остается, что на Чернове белый костюм, покажем это условие ребром. Так как белый костюм уже занят, то остается Серову – черный, а Белову – серый, покажем это тоже ребрами. Итак, мы решили задачу с построением несвязного графа (рис.46), который содержит 6 вершин и 3 ребра. рис.46

1. В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым.

Решение: Задача решается аналогично предыдущей задачи с построением несвязного графа (рис.47), который содержит 6 вершин и 3 ребра. Ключевая фраза, которая помогает решить задачу: «Сергей живет в одном доме Петровым», значит Сергей не Петров. Ребра и показывают ответ задачи. рис.47

1. Три друга Алеша, Боря и Вова после школы едут домой на различном транспорте: автобусе, маршрутке, трамвае. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходила  маршрутка, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!» Кто на чем ездит домой?

Решение: Задача отличается от предыдущей задачи тем, что в ней несколько ключевых фраз, но решается тоже с построением несвязного графа (рис.48), который содержит 6 вершин и 3 ребра. Первая ключевая фраза, которая помогает решить задачу: «Алеша пошел проводить своего друга до остановки автобуса», значит Алеша ездит не на автобусе. Вторая ключевая фраза: «Когда мимо них проходила  маршрутка», значит Алеша ездит не на маршрутке. Остается – Алеша на трамвае. Третья ключевая фраза: «третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!»», значит друг, которого провожал Алеша до автобуса – Боря, а Вова едет на маршрутке. Ребра и показывают ответ задачи.

рис.48

1. Андрей, Борис, Витя и Гриша – друзья. Один из них – врач, другой – журналист, третий – тренер, четвертый – строитель. Журналист написал статьи об Андрее, Борисе и Грише. Тренер и журналист вместе с Борисом ходили в поход. Андрей и Борис были на приеме у врача. У кого какая профессия?

Решение: В данной задаче граф будет состоять из 8 вершин и 4 ребер. Первая ключевая фраза, которая помогает решить задачу: «Журналист написал статьи об Андрее, Борисе и Грише», значит журналист это Витя. Вторая ключевая фраза: «Тренер и журналист вместе с Борисом ходили в поход», значит Борис не тренер и не журналист. Третья ключевая фраза: «Андрей и Борис были на приеме у врача», значит врач не Андрей и не Борис. Так как больше с условием задачи работать нельзя, то будем работать по графу. По графу видно, что Борис не врач, не журналист, не тренер, а значит – строитель (рис.49). Андрей – не врач, но и не журналист (Витя) и не строитель (Борис), а значит – тренер. А Грише остается врач. Ребра и показывают ответ задачи (рис.50).

рис.49 рис.50

1. Три подруги Тамара, Валя и Лида были в белом, красном и голубом платьях. Их туфли были тех же цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и цвет туфель каждой из подруг.

Решение: В данной задаче граф будет состоять из 9 вершин и 6 ребер. Причем вершины надо разбить на три тройки: первая – имена, вторая – цвет туфель, третья – цвет платья и разместить их для наглядности в разных плоскостях (рис.51). Первая ключевая фраза, которая помогает решить задачу: «Валя была в белых туфлях», значит проводим первое ребро от Вали до белых туфель. Вторая ключевая фраза: «Ни платье, ни туфли Лиды не были красными», значит проводим пунктиры от Лиды до красных туфель и красного платья. Третья ключевая фраза: «Только у Тамары цвета платья и туфель совпадали», значит у Вали не белое платье (так как у нее белые туфли). Так как больше с условием задачи работать нельзя, то будем работать по графу (рис.52). По графу видно, что у Лиды голубые туфли (так как красные быть не могут, а белые у Вали), значит, проводим второе ребро. Далее видно, что Тамаре остаются красные туфли и значит и красное платье (третья ключевая фраза), проводим еще два ребра. У Вали голубое платье (так так красное у Тамары, а белое не может быть по графу). Остается Лиде белое платье, проводим последнее ребро. Ребра и показывают ответ задачи (рис.53).

рис. 51 рис.52 рис. 53

1. Три друга – Леша, Сергей и Денис – купили щенков разной породы: щенка такса, щенка колли и щенка овчарки. Известно, что: щенок Леши темнее по окрасу, чем такса, Леси и Гриф; щенок Сергея старше Грифа, овчарки и таксы; Джек и такса всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.

Решение: В данной задаче граф будет состоять из 9 вершин и 6 ребер. Причем вершины надо разбить на три тройки: первая – имена, вторая – клички, третья – порода и разместить их для наглядности в разных плоскостях. Первая ключевая фраза, которая помогает решить задачу: «: щенок Леши темнее по окрасу, чем такса, Леси и Гриф», значит у Леши не такса, не Леси, не Гриф. Вторая ключевая фраза: «щенок Сергея старше Грифа, овчарки и таксы», значит у Сергея не Гриф, не овчарка, не такса. Третья ключевая фраза: «Джек и такса всегда гуляют вместе», значит Джек это не такса. Так как больше с условием задачи работать нельзя, то будем работать по графу. По графу видно, что у Сережи не такса и не овчарка, а значит – колли, поэтому проводим первое ребро. Далее видно, что у Леши не такса и не колли, а значит - овчарка, проводим еще ребра. Денису осталась такса. У Леши не Леси и не Гриф, значит Джек. У Сережи не Гриф и не Джек, а Леси. Остается Денису Гриф, проводим последнее ребро. Ребра и показывают ответ задачи (рис.54).

рис.54

1.  В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд?

Решение: Решением задачи будет несвязный граф, состоящий из трех граф-деревьев (рис.55). Первым звеном графа будут горячие блюда, вторым – гарнир, третьим – напитки. По графу легко составить все возможные комбинации обедов: Щ-К-Ч, Щ-К-К, Щ-Р-Ч, Щ-Р-К, Г-К-Ч, Г-К-К, Г-Р-Ч, Г-Р-К, Б-К-Ч, Б-К-К, Б-Р-Ч, Б-Р-К – 12 вариантов. рис.55

1. Алла решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить их или в вазу или в кувшин. Сколькими способами это можно сделать?

Решение: Решением задачи будет несвязный граф, состоящий из трех граф-деревьев (рис.56). Первым звеном графа будут цветы, вторым – сосуды. По графу легко составить все возможные комбинации букетов: Р-В, Р-К, Т-В, Т-К, Г-В, Г-К – 6 способов. рис.56

1. Из наборного полотна взяли две карточки с цифрой 1 и три карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек?

Решение: Решением задачи будет несвязный граф, состоящий из двух граф-деревьев (рис.57). В каждом граф-дереве будет по 5 звеньев, так как надо составить пятизначное число. По графу легко посчитать, что можно составить 10 чисел. рис.57

1. У Левы 2 конверта: обычный и авиа и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами он может выбрать конверт и марку, чтобы отправить письмо?

Решение: Решением задачи будет несвязный граф, состоящий из двух граф-деревьев (рис.58). В каждом граф-дереве будет по 2 звена. Первое звено – тип конверта, второе – тип марки. По графу легко посчитать, что возможно 6 вариантов. рис.58

. 
Проанализировав выше предложенный практический материал, приходим к выводу, что для решения задач, с применением теории графов, можно выделить следующие этапы:

1. Анализ условия задачи и перевод ее на язык графов;

2. Геометрическая интерпретация условия, построение графа. Именно на этом этапе  очень важен элемент творчества потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа;

• Точками обозначают объекты задачи (вершины графа). Если в задачах дано несколько групп объектов, то лучше их изображать в разных плоскостях и различными цветами;

• Линиями (отрезками, дугами) обозначают отношения между объектами (рёбра графа). Отношения могут быть двух типов: принадлежит и не принадлежит. Если отношение «принадлежит», то линии сплошные, если отношение «не принадлежит» - пунктирные;

1. Выделяем ключевые фразы задач и, анализируя их, проводим ребра;

2. Если ключевых фраз не достаточно для решения задачи, то анализируем граф и проводим недостающие ребра;

3. Выбираем нужные отношения (сплошные линии) и записываем ответ.

Использование графов в качестве некоторого вспомогательного средства позволяет облегчить процесс обучения и подготовить учеников к восприятию сложных тем в курсе школьной математики. Графовые задачи, без сомнения, нужно использовать не только на математических кружках, при подготовке к олимпиадам для развития сообразительности учеников, но и использовать теорию графов как языка на уроках математики, алгебры, геометрии, информатики для повышения качества обучения.

Таким образом, применяя теорию графов в школьном курсе математики, решение многих математических задач и доказательств упрощается, придает им наглядность и простоту.

 

     

Использованные материалы и Интернет-ресурсы

1. Нагибин Ф.Ф. Применение графов для решения логических задач.

// Математика в школе. — 1964. — № 3.

1. Гуровиц В.М., Ховрина В.В. Графы.-М.:МЦНМО, 2008.- 32 с.:ил.

2. П.В. Севрюков Подготовка к решению олимпиадных задач по математике: Илекса, 2001

3. http://sch216.narod.ru/nayka/doc/graf.htm

4. http://dok.opredelim.com/docs/index-3239.html

5. http://festival.1september.ru/articles/416943/

6. http://kk.docdat.com/docs/index-487830.html

7. http://pandia.ru/text/78/009/77971.php

8. http://player.myshared.ru/4/191256/data/images/img4.png

9. http://www.vevivi.ru/best/Obuchenie-resheniyu-matematicheskikh-zadach-s-pomoshchyu-grafov-ref43062.html

10. http://www.igry-detei.ru/uploads/24.png

11. http://nsportal.ru/shkola/algebra/library/2013/03/09/teoriya-grafov-teoriya-i-zadachi

Приложения:

1. Ранним утром Оля, Маша, Катя обменялись приветствиями каждый с каждым. Сколько всего было приветствий.
2. Андрей, Борис, Виктор и Георгий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

3. Аркадий, Борис, Георгий, Владимир и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому один раз). Сколько всего рукопожатий сделано?

4. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий?

5. На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего рукопожатий было сделано?

6. В шахматном турнире участвовало семь человек. Каждый с каждым сыграл по одной партии. Сколько партий они сыграли?

7. В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей. Боря сыграл с Аней и Гришей, Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось?

8. В стране алфавит 8 городов: А, Б, В, Г, Д, Е, Ж, З и 8 непересекающихся дорог между городами А и Б, Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З, В и Е. Можно ли по этим дорогам проехать из А в Г?

9. Крас­ный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша от­личается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

10. На столе лежат в ряд четыре фигуры: треугольник, ромб, круг, квадрат. Цвета этих фигур – зеленый, желтый, синий, красный. В каком порядке лежат фигуры и каков цвет каждой из них, если фигура красного цвета лежит между зеленой и синей. Справа от желтой фигуры лежит ромб, круг лежит правее треугольника и ромба, причем треугольник лежит не с краю, и, наконец, фигура синего цвета не лежит рядом с фигурой желтого цвета?

11. В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша. Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.

12. На улице, став в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая девочка?

13. На одном заводе работают три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика.

14. В пионерский лагерь приехали три друга Миша, Володя и Петя. Известно, что каждый из них имеет одну из фамилий: Иванов, Семенов и Герасимов. Миша не Герасимов, отец Володи инженер, Володя учится в 6-м классе. Герасимов учится в 5-м классе. Отец Иванова слесарь. Какая фамилия у каждого из ребят?

15. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая жидкость?

16.  В нашем лесу каждый занят своим делом: одни плетут корзины, другие ловят рыбу. Ремеслу мы учились друг у друга. Кот учился у Выдры, Еж - у Зайца, Лиса- у Волка, а Мышь- у Ежа. Бобер учил Волка и Выдру, Заяц- Белку, а Барсук- Зайца. Бобер был учеником Медведя, а Еж учителем Дятла. Лучше всех плетет корзины Еж. Чем занимались Заяц, Дятел, Волк, и Лиса? Кто из зверей нашего леса раньше всех научился ловить рыбу, а кто - плести корзины? 

17. На карточке  нарисованы: отрезок, круг, треугольник, звезда, квадрат. В каком порядке они нарисованы, если известно, что отрезок располагается не рядом с треугольником, треугольник - не рядом с кругом, круг - не рядом со звездой, а звезда- не рядом с отрезком, треугольник- не рядом с квадратом, а квадрат- не рядом с кругом, звезда- рядом с квадратом, слева от него?

18. Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4. Сколько вариантов придется перебрать им, чтобы подобрать двузначный код?
19. Сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?
20. Антон, Борис и Василий купили 3 билета на 1-е, 2-е, 3-е места первого ряда на футбольный матч. Сколькими способами они могут занять места?

21. В пятницу 4 урока: алгебра, русский, физика и история. Сколькими способами можно составить расписание на пятницу?

22. Катя, Галя и Оля, играя, спрятали по игрушке. Они играли с медвежонком, зайчиком и слоником. Известно, что Катя не прятала зайчика, а Оля не прятала ни зайчика, ни медвежонка.
    У кого какая игрушка?

23. Коля, Боря, Вова и Юра заняли первые четыре места в соревновании, причём никакие два мальчика не делили между собой одно и тоже место. На вопрос, какие места заняли ребята, трое ответили: Коля - не первое и не четвёртое; Боря - второе; Вова - не был последним.
    Какое место занял каждый из мальчиков?

24. Три поросенка построили три домика из соломы, из прутьев, из камней. Каждый из них получил один домик: Ниф-Ниф – не из камней, и не из прутьев; Нуф-Нуф не из камней.
    Какой домик достался Наф-Нафу.

25. Четыре брата Юра, Петя, Вова, Коля учатся в 1,2,3,4 классах. Петя- отличник, младшие братья стараются брать с него пример. Вова учится в 4 классе. Юра помогает решать задачи брату.
    Кто в каком класе учится?

26. В семье трое детей: 2 мальчика и девочка. Их имена начинаются с букв А,В,Г. Среди А и В есть начальная буква имени одного мальчика, а среди В и Г – начальная буква имени другого мальчика.
    С какой буквы начинается имя девочки?

27. Нюша , Бараш, Копатыч и Лосяш играли с мячами синим, зелёным, жёлтым и красным.
    Каким из мячей играл каждый из них, если мяч Бараша не синий, у Нюши не синий и не красный, а у Копатыча желтый мяч?

28. Старый гном разложил свои сокровища в 3 разноцветных сундука, стоящих у стены.
    В один – драгоценные камни, в другой – золотые монеты, а в третий – магические книги.
    Он помнит, что красный сундук правее, чем драгоценные камни.
    А магические книги правее, чем красный сундук.
    В каком сундуке лежат магические книги, если зелёный сундук стоит левее, чем синий?