Фос 9класс геометрия 2024-2025уч.год

Геометрия 9 класс

Контрольная работа № 1 по теме: «Векторы»

9 класс

Вариант 1.

1. Начертите два неколлинеарных вектора 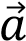и 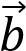. Постройте векторы, равные:

а) 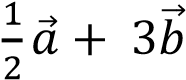; б) .

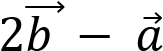1. На стороне ВС ромба ABCD лежит точка К так, что ВК=КС, О – точка

пересечения диагоналей. Выразите векторы 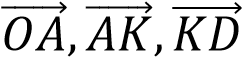через векторы = .

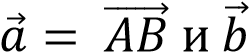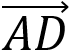3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.

Вариант 2.

1. Начертите два неколлинеарных вектора 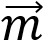и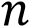 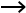. Постройте векторы, равные:

а) 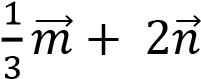; б)

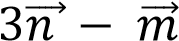
1. На стороне СD квадрата ABCD лежит точка P так, что CP = PD, О – точка пересечения диагоналей. Выразите векторы 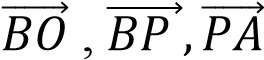через векторы

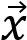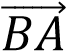= и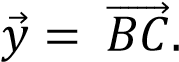

3. В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.

Контрольная работа №2 по теме:

«Соотношение между сторонами и углами треугольника»

Вариант 1.

1. Найдите угол между лучом ОА и положительной полуосью Ох, если А (-1;3).

2. Решите треугольник АВС, если

3. Найдите косинус угла М треугольника KLM, если К (1;7), L(-2;4), M (2;0).

Вариант 2.

1. Найдите угол между лучом ОВ и положительной полуосью Ох, если В (3;3).

2. Решите треугольник ВСD, если

3. Найдите косинус угла A треугольника ABC, если A (3;9), B(0;6), C (4;2).

Контрольная работа №3 по теме:

«Длина окружности и площадь круга»

Вариант 1.

1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

2. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72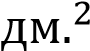

3. Найдите длину дуги окружности радиуса 3 см, если её градусная мера равна 150°.

Вариант 2.

1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 см.

2. Найдите сторону квадрата, вписанного в ту же окружность.

Найдите длину окружности, если площадь вписанного в неё правильного шестиугольника равна 72 .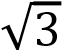

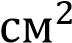3. Найдите площадь кругового сектора, если градусная мера его дуги равна 120°, а радиус круга равен 12 см.

Контрольная работа № 4 по теме: «Движение»

9 класс

Вариант 1

1. Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ.

2. Две окружности с центрам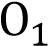и и 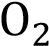, радиусы которых равны, пересекаются в точках M и N. Через точку М проведена прямая, параллельная 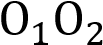и пересекающая окружность с центром 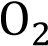в точке D. Используя параллельный перенос, докажите, что четырёхугольник 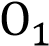MD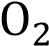 является параллелограммом.

Вариант 2

1. Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны CD.

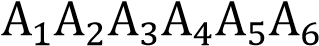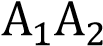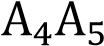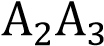2. Дан шестиугольник . Его стороны и , и ,

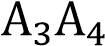
и 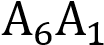попарно равны и параллельны. Используя центральную симметрию,

докажите, что диагонали 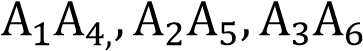данного шестиугольника пересекаются в одной точке.

Итоговая контрольная работа № 5

Вариант 1.

1. Какое утверждение относительно треугольника со сторонами 5,9,15 верно?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2. Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен: а) 25 см; б) 40 см; в) 32 см; г) 20 см.

3. Если один из углов ромба равен 60°, а диагональ, проведённая из вершины этого угла, равна4√3 см, то периметр ромба равен:

а) 16 см; б) 8 см; в) 12 см; г) 24 см.

4. Величина одного из углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника.

а) 84°; б) 92°; в) 80°; г) 87°.

5. В треугольнике АВС сторона а=7, сторона b=8, сторона с=5. Вычислите угол А.

а) 120°; б) 45°; в) 30°; г) 60°.

Вариант 2

1. Какое утверждение относительно треугольника со сторонами 12,9,15 верно?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2. Если сходственные стороны подобных треугольников равны 2 см и 5 см, площадь первого треугольника равна 8 〖 см〗 ^2 , то площадь второго треугольника равна: а) 50 〖 см〗 ^2 ; б) 40 〖 см〗 ^2 в) 60 〖 см〗 ^2; г) 20〖 см〗 ^2 .

3. Если в равнобедренном треугольнике длина основания равна 12 см, а его периметр равен 32 см , то радиус окружности, вписанной в треугольник, равен::

а) 4 см; б) 3 см; в) 6 см; г) 5 см.

4. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите катеты треугольника.

а)12 см и 16 см; б)7 см и 11 см; в) 10 см и 13 см; г) 8 см и 15 см.

5. Стороны прямоугольника равны a и k. Найдите радиус окружности, описанной около этого прямоугольника.

а) а^2/k; б) k^2/a; в) 1/2 √(а^2+k^2 ); г) √(а^2+k^2 ).