Просмотр содержимого документа
«Фрагмент урока геометрии в 7 классе по теме "Окружность" с практико-ориентированным заданием (математическая грамотность)»
Разработка фрагмента урока
МКОУ «Кремяновская СОШ»
Учитель математики Кабанкова О.С.
Предмет: Математика
Класс: 7
Тема урока: Окружность
Тип урока: урок применения знаний, умений и навыков
Используемая технология: системно – деятельностного подхода.
Цель урока: образовательная: изучение понятия окружности и ее элементов, установление зависимости между длиной окружности и её диаметром, вывод формулы длины окружности.
развивающая: развитие познавательного интереса, навыков исследовательской работы, умения работать в команде
воспитательная: воспитание самостоятельности, чувства ответственности за качество и результат выполняемой работы.
Задачи урока:
усилить прикладную направленность;
формировать математическую грамотность школьников;
продолжить работу над развитием вычислительных навыков;
создать условия для развития функциональной грамотности.
Планируемые результаты:
Личностные:
- формирование умения ясно, точно, грамотно излагать свои мысли, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры;
- развитие креативности мышления, инициативы, находчивости, активности при решении математических задач;
- развитие способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Метапредметные:
- формирование умения видеть математическую задачу в контексте проблемной ситуации в окружающей жизни;
- формирование умения планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Предметные:
-формирование теоретических и практических представлений об окружности и круге, как о геометрических фигурах, их элементах;
-формирование умений применения изученных понятий для решения задач практического характера.
Оборудование урока:
1. Карточки-задания (приложение 1);
2. Ноутбук, проектор.
Технологическая карта урока
| Этап | Деятельность учителя, педагога | Деятельность ученика, воспитанника |
| Организационный момент Создание условий для осознанного вхождения обучающихся в пространство деятельности на уроке
| Приветствует учащихся с целью создания благоприятной атмосферы урока. | Настраиваются на урок и восприятие материала. |
| Подготовка учащихся к работе на основном этапе урока Мотивация учебной деятельности обучающихся | Подводит учащихся к формулировке темы урока | Определяют и формулируют тему урока |
| Постановка цели и задач | Побуждает учащихся к высказыванию своего мнения. Подводит учащихся к составлению плана изучения темы. | Пытаются сформулировать цели, составляют план изучения для построения нового знания. |
| Актуализация знаний | Организует работу по созданию в памяти системы опорных знаний и умений для осознанного восприятия новых знаний. | Вступают в диалог. |
| Применение знаний, умений и навыков по теме Самостоятельная деятельность обучающихся по применению знаний (практикум) |
Организует учебное взаимодействие учащихся в группах для закрепления знаний по теме. Выступает в роли консультанта. |
Ищут способы решения учебной задачи. Определяют план своих действий. Участвуют в обсуждении содержания материала, переходят к выполнению практического задания. |
| Физкультминутка | Учитель проговаривает стих и показывает движения учащимся. | Учащиеся выполняют физкультминутку вместе с учителем. |
| Представление итогов работы | Учитель осуществляет промежуточный контроль выполнения заданий практикума. | Представители групп отчитываются после выполнения каждого задания. |
| Рефлексия
| Побуждает учащихся к рефлексии. | Рефлексия своих действий. |
Приложение 1
Практикум Решение практических задач"Ремонт комнаты"
Прочитайте внимательно текст. Затем приступайте к выполнению заданий, выбирая нужный вариант ответа и отмечая его на карточке.
| Ремонт комнаты Задание 1 / 4
Прочитайте текст «Ремонт комнаты», расположенный справа. Запишите свои ответы на вопросы в виде чисел.
Ширина рулона меньше длины и меньше ширины комнаты, поэтому, чтобы полностью покрыть пол комнаты, надо выложить вплотную один к другому несколько кусков ковролина перпендикулярно стене с окном.
А) Сколько кусков ковролина придётся выложить?
Запишите свой ответ в виде числа.
шт.
Б) Какова длина одного такого куска?
Запишите свой ответ в виде числа.
м
В) Какого наименьшего количества метров ковролина будет достаточно, чтобы полностью застелить пол в комнате Марии?
Запишите свой ответ в виде числа. | РЕМОНТ КОМНАТЫ
Семья Марии делает ремонт в её комнате. План комнаты с замерами, которые сделала Мария, представлен ниже.
Комната имеет неправильную форму: три прямых угла, а вместо четвёртого угла она имеет стену округлой формы.
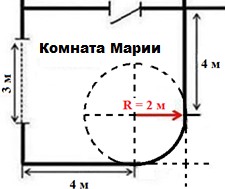 
Для покрытия пола Мария выбрала ковролин. Ковролин продают в рулонах, от которых покупатель может попросить отрезать необходимое ему количество метров. Ширина рулона – 2 м.
Планируется полностью покрыть пол комнаты ковролином, без зазоров и нахлёстов.
Для справок: С = 2𝜋𝜋𝜋𝜋 − длина окружности, 𝑆𝑆 = 𝜋𝜋𝜋𝜋2 −площадь круга, где 𝜋𝜋 − радиус круга. Считайте, что 𝜋𝜋 = 3,14.
|
| Ремонт комнаты Задание 2 / 4
Воспользуйтесь текстом «Ремонт комнаты», расположенным справа. Запишите свой ответ на вопрос в виде числа, а затем приведите решение.
Из-за того, что один из углов комнаты «круглый», ковролин обрезают по форме скругления.
Какова площадь остатков ковролина, получившихся в результате скругления?
Запишите свой ответ в виде числа. Ответ дайте в м2.
м2
Приведите решение. | РЕМОНТ КОМНАТЫ
Семья Марии делает ремонт в её комнате. План комнаты с замерами, которые сделала Мария, представлен ниже.
Комната имеет неправильную форму: три прямых угла, а вместо четвёртого угла она имеет стену округлой формы.
 
Для покрытия пола Мария выбрала ковролин. Ковролин продают в рулонах, от которых покупатель может попросить отрезать необходимое ему количество метров. Ширина рулона – 2 м.
Планируется полностью покрыть пол комнаты ковролином, без зазоров и нахлёстов.
Для справок: С = 2𝜋𝜋𝜋𝜋 − длина окружности, 𝑆𝑆 = 𝜋𝜋𝜋𝜋2 −площадь круга, где 𝜋𝜋 − радиус круга. Считайте, что 𝜋𝜋 = 3,14. |


| Ремонт комнаты Задание 3 / 4
Воспользуйтесь текстом «Ремонт комнаты», расположенным справа. Запишите свой ответ на вопрос в виде числа.
От рулона шириной 2 м отрезан кусок длиной 5 м. Какова наибольшая площадь комнаты (в квадратных метрах), пол которой можно полностью покрыть этим ковролином?
Запишите свой ответ в виде числа.
м2 | РЕМОНТ КОМНАТЫ
Семья Марии делает ремонт в её комнате. План комнаты с замерами, которые сделала Мария, представлен ниже.
Комната имеет неправильную форму: три прямых угла, а вместо четвёртого угла она имеет стену округлой формы.
 
Для покрытия пола Мария выбрала ковролин. Ковролин продают в рулонах, от которых покупатель может попросить отрезать необходимое ему количество метров. Ширина рулона – 2 м.
Планируется полностью покрыть пол комнаты ковролином, без зазоров и нахлёстов.
Для справок: С = 2𝜋𝜋𝜋𝜋 − длина окружности, 𝑆𝑆 = 𝜋𝜋𝜋𝜋2 −площадь круга, где 𝜋𝜋 − радиус круга. Считайте, что 𝜋𝜋 = 3,14. |

| Ремонт комнаты Задание 4 / 4
Воспользуйтесь текстом «Ремонт комнаты», расположенным справа. Отметьте нужный вариант ответа, а затем объясните свой ответ.
По периметру комнаты планируется проложить плинтус. Хватит ли 24 м плинтуса для этой комнаты?
Объясните свой ответ. | РЕМОНТ КОМНАТЫ
Семья Марии делает ремонт в её комнате. План комнаты с замерами, которые сделала Мария, представлен ниже.
Комната имеет неправильную форму: три прямых угла, а вместо четвёртого угла она имеет стену округлой формы.
 
Для покрытия пола Мария выбрала ковролин. Ковролин продают в рулонах, от которых покупатель может попросить отрезать необходимое ему количество метров. Ширина рулона – 2 м.
Планируется полностью покрыть пол комнаты ковролином, без зазоров и нахлёстов.
Для справок: С = 2𝜋𝜋𝜋𝜋 − длина окружности, 𝑆𝑆 = 𝜋𝜋𝜋𝜋2 −площадь круга, где 𝜋𝜋 − радиус круга. Считайте, что 𝜋𝜋 = 3,14. |

Приложение 2
Характеристика заданий и система оценивания
Решение практических задач "Ремонт квартиры»
Характеристики заданий и система оценивания
| ЗАДАНИЕ 1. РЕМОНТ КОМНАТЫ (1 из 4). МФГ_МА_7_002_01_А8 |
| ХАРАКТЕРИСТИКИ ЗАДАНИЯ: Содержательная область: пространство и форма Компетентностная область: формулировать Контекст: личный Уровень сложности: средний Формат ответа: задание с несколькими краткими ответами Объект оценки: составление фигуры из заданных элементов с учётом их линейных размеров Максимальный балл: 2 |
| Система оценивания: |
| Балл | Содержание критерия |
| 2 | Ответ: А) 3; Б) 6 м; В) 18 м. (Если наименования отсутствуют, ответ принимается.) Даны 3 верных ответа |
| 1 | Даны верные ответы на любые два вопроса, на один из вопросов ответ неверный или отсутствует. |
| 0 | Другие ответы |
| ЗАДАНИЕ 2. РЕМОНТ КОМНАТЫ (2 из 4). МФГ_МА_7_002_02_А8 |
| ХАРАКТЕРИСТИКИ ЗАДАНИЯ: Содержательная область: пространство и форма Компетентностная область: применять Контекст: личный Уровень сложности: высокий Формат ответа: задание с кратким и развернутым ответом Объект оценки: вычисление площади фигуры сложной формы, использование свойства аддитивности площади Максимальный балл: 2 |
| Система оценивания: |
| Балл | Содержание критерия |
| 2 | Ответ: 0,86 (м2); Пример возможного решения: 1) 2 х 2 = 4 (м2); 2) 3,14 х 4 : 4 = 3,14 (м2); 3) 4-3,14 = 0,86 (м2). Или дано любое аналогичное решение. Дан верный ответ и приведено верное решение. |
| 1 | Дан верный ответ (0,86 м2) без пояснения; ИЛИ в логически верном решении допущена арифметическая ошибка, в результате которой дан неверный ответ; ИЛИ дан ответ 1 (м2) и логически верное решение, где π округлено до 3. |
| 0 | Другие ответы. |
| ЗАДАНИЕ 3. РЕМОНТ КОМНАТЫ. (3 из 4) МФГ_МА_7_002_03_А8 |
| ХАРАКТЕРИСТИКИ ЗАДАНИЯ: Содержательная область оценки: пространство и формы Компетентностная область оценки: формулировать Контекст: образовательный Уровень сложности задания: низкий Формат ответа: задание с кратким ответом Объект оценки: вычислять площадь прямоугольника Максимальный балл: 1 |
| Система оценивания: |
| Балл | Содержание критерия |
| 1 | Записано число 10. |
| 0 | Другой ответ или ответ отсутствует. |
| ЗАДАНИЕ 4. РЕМОНТ КОМНАТЫ. (4 из 4) МФГ_МА_7_002_04_А8 |
| ХАРАКТЕРИСТИКИ ЗАДАНИЯ: Содержательная область оценки: пространство и формы Компетентностная область оценки: рассуждать Контекст: образовательный Уровень сложности задания: низкий Формат ответа: комплексное задание с выбором ответа и объяснением Объект оценки: вычислять, оценивать периметр фигуры, составленной из элементов квадрата и круга Максимальный балл:1 |
| Система оценивания: |
| Балл | Содержание критерия |
| 1 | Выбран ответ «Хватит» и приведено верное обоснование. Возможные обоснования: Вариант 1: Периметр комнаты квадратной формы – 6 х 4 = 24 м. Периметр данной комнаты меньше, т.к. длина стены округлой формы меньше обычных прямолинейных участков стены и еще надо вычесть ширину двери. Вариант 2: Периметр данной комнаты равен 6 х 3 + 2 х 3,14 х 2 : 4 ≈ 21,14 (м) 24 м. |
| 0 | Другой ответ или ответ отсутствует. |





















