Графический метод решения задач с параметрами

Графический метод решения задач с параметрами

Подготовила учитель математики МБОУ СОШ №3 Быканова Т.Н.

Математическое понятие параметра

Параметром называются коэффициенты при неизвестных или свободные члены, заданные не конкретными числовыми значениями, а обозначенные буквами.

Решить задачу с параметром – это значит, для каждого значения параметра найти значения x , удовлетворяющие условию этой задачи.

Основные способы решения задач

с параметром

Графический.  

Решение относительно параметра.

В зависимости от задачи (с переменной x и параметром a ) рассматриваются графики или в координатной плоскости (Оxy), или в координатной плоскости (Оx a ).

Переменные x и a принимаются равноправными и выбирается та, относительно которой аналитическое решение признается более простым.

Аналитический.

  Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра.

Преимущества графического метода решения задач с параметром.

отсутствие сложных и громоздких вычислений

экономия времени

подсказка на более рациональный

аналитический

метод решения

1. При каких значениях параметра a уравнение   имеет ровно 2 различных решения?

• Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю. Получим систему:

• В первом уравнении выделим полный квадрат:

• Это уравнение окружности с центром в точке    и радиусом равным 2. Уравнение    задает прямую, проходящую через начало координат. Графики будем строить в системе координат Оха.

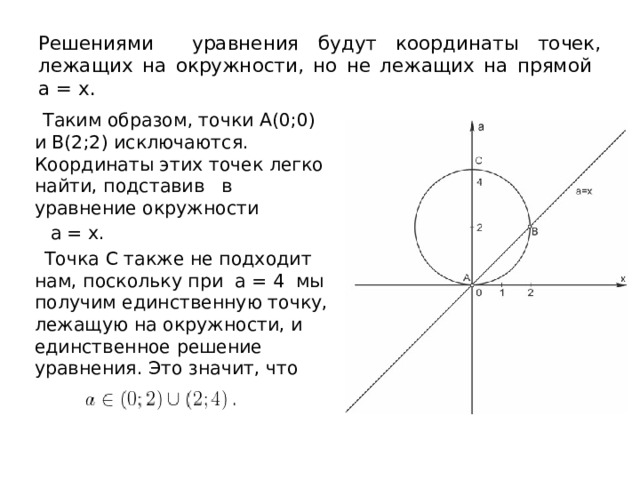
Решениями уравнения будут координаты точек, лежащих на окружности, но не лежащих на прямой a = x.

Таким образом, точки А(0;0) и В(2;2) исключаются. Координаты этих точек легко найти, подставив   в уравнение окружности

a = x.

Точка С также не подходит нам, поскольку при  a = 4 мы получим единственную точку, лежащую на окружности, и единственное решение уравнения. Это значит, что

2. Найдите все значения a, при которых уравнение   имеет единственное решение .

Уравнение равносильно системе:

Мы возвели обе части уравнения в квадрат при условии, что   

Раскроем скобки в правой части уравнения, получим систему

Приведём подобные слагаемые в уравнении, получим

Добавим к левой и правой частям уравнения 49 и выделим в правой части полные квадраты, получим уравнение

Это уравнение   задает окружность с центром в точке  Р (7; -7), где радиус 

Неравенство    задает полуплоскость, которая расположена выше прямой  , вместе с самой этой прямой.

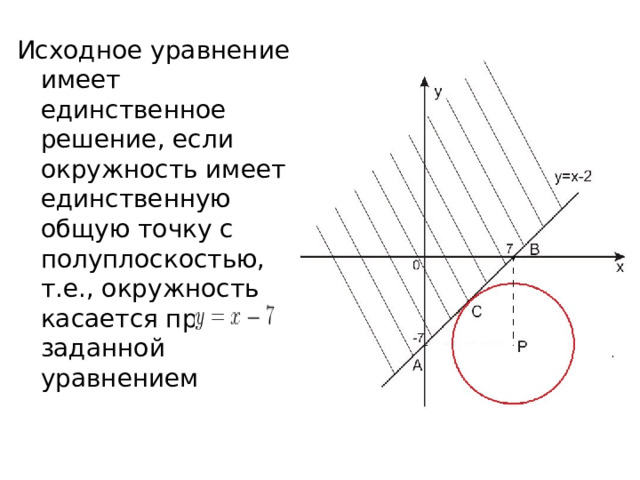
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью, т.е., окружность касается прямой, заданной уравнением 

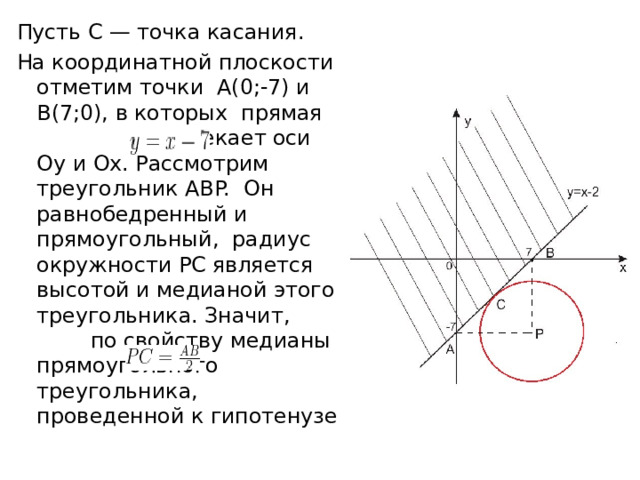
Пусть С — точка касания.

На координатной плоскости отметим точки  А(0;-7) и В(7;0), в которых прямая    пересекает оси Оy и Ox. Рассмотрим треугольник ABP. Он равнобедренный и прямоугольный, радиус окружности PC является высотой и медианой этого треугольника. Значит,   по свойству медианы прямоугольного треугольника, проведенной к гипотенузе

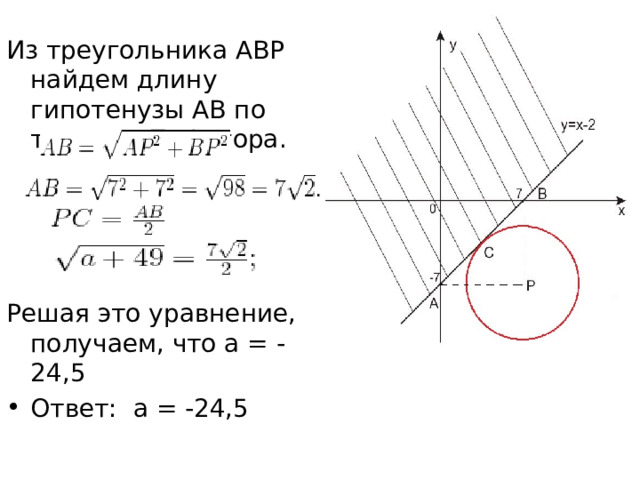
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.

Решая это уравнение, получаем, что а = -24,5

• Ответ:  а = -24,5

3. Найдите все положительные значения параметра а, при каждом из которых система

имеет единственное решение.

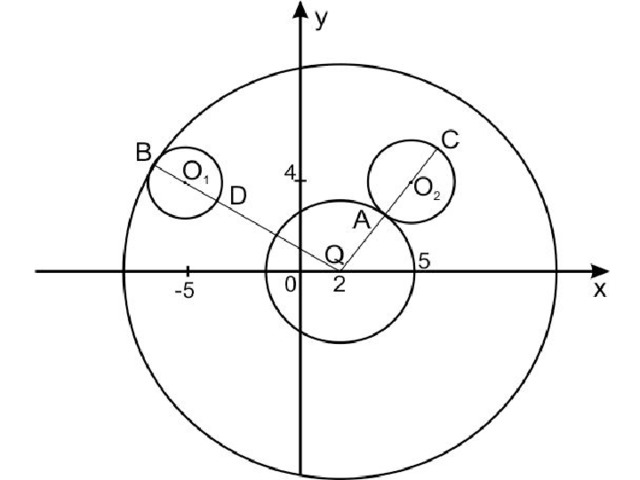
Графиком уравнения 

являются две симметричные окружности  и с центрами в точках О₁(-5; 4) и О₂(5;4) радиуса 2. Второе уравнение при а˃0  задает окружность  с центром в точке  Q(2;0)  и радиусом a.

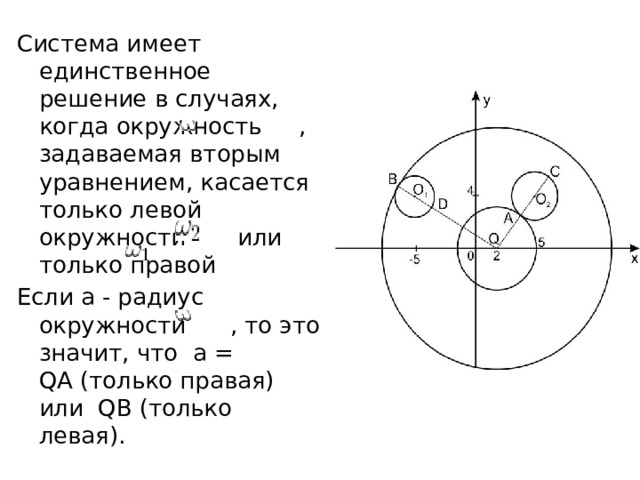
Система имеет единственное решение в случаях, когда окружность   , задаваемая вторым уравнением, касается только левой окружности     или только правой 

Если a - радиус окружности   , то это значит, что  а = QA (только правая) или  QB (только левая).

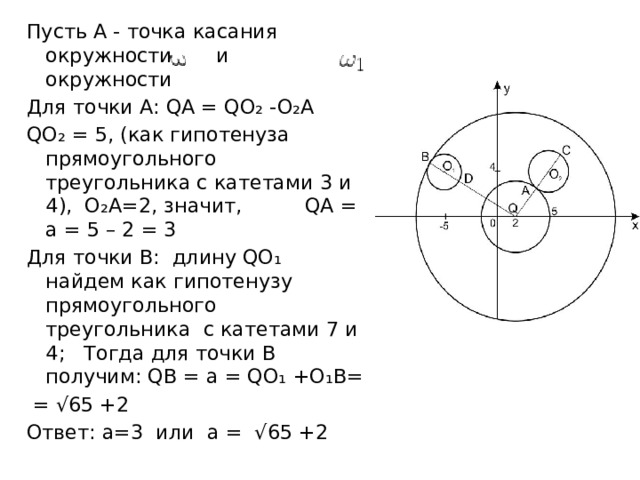
Пусть А - точка касания окружности     и окружности 

Для точки А: QA = QO₂ -O₂A

QO₂ = 5, (как гипотенуза прямоугольного треугольника с катетами 3 и 4),  O₂A=2, значит, QA = а = 5 – 2 = 3

Для точки В:  длину QО₁ найдем как гипотенузу прямоугольного треугольника с катетами 7 и 4;   Тогда для точки В получим: QВ = а = QО₁ +О₁В=

= √65 +2

Ответ: а=3  или  а = √65 +2