Тема. «Графики функций вида у = ах2 +n, у = a (х - m)2 , у = a (х - m)2 + n»
Ход урока.
Самостоятельная работа.
| Вариант1 Построить линии, симметричные данным относительно оси ОУ 
| 2.Функция задана формулой у= 3х2. а) Найдите у(5). б) При каких значениях х значение функции равно 12? в) Определите, принадлежат ли графику данной функции точки А(1;-3). В (-1;3)? 3. Постройте график функции у= -3х2.
|
| Вариант2 1. Построить линии, симметричные данным относительно оси ОХ 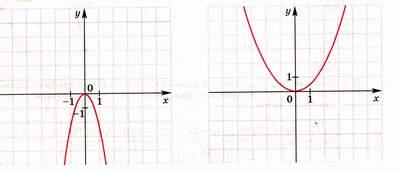
| 2.Функция задана формулой у= -2х2. а) Найдите у(3). б) При каких значениях х значение функции равно -50? в) Определите, принадлежат ли графику данной функции точки А(1;-2). В (-1;2)? 3. Постройте график функции у= 2х2.
|
| Вариант 3. 1. Разложите квадратный трёхчлен 3х2 +2х -5 на множители. 2. Постройте график функции у= 0,5х2. Укажите промежутки возрастания функции. 3. Найдите координаты точек пересечения графика функции у= х2 + 4х -5 с осями координат.
| Вариант5. 1)Приведите основные свойства и график функции у=ах2 при а0. 2)Постройте график функции у=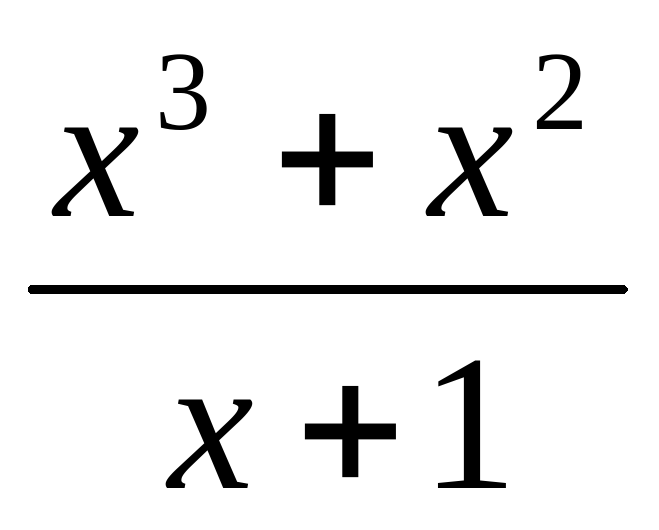 . . 3) При каком значении а прямая у= х+а касается параболы у = 0,5 х2? |
| Вариант 4 1. Разложите квадратный трёхчлен 7х2 -5х -2 на множители. 2. Постройте график функции у= -0,5х2. Укажите промежутки возрастания функции. 3. Найдите координаты точек пересечения графика функции у= -х2 + 4х -3 с осями координат.
| Вариант 6. 1) Приведите основные свойства и график функции у=ах2 при а 2)Постройте график функции у=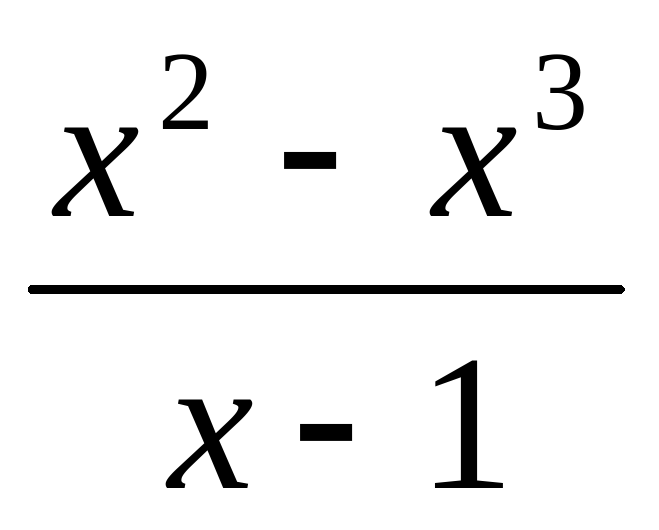 . . 3) При каком значении а прямая у= х-а касается параболы у = -2 х2? |
Объяснение нового материала.
1)Мы знаем , как выглядит график функции у = 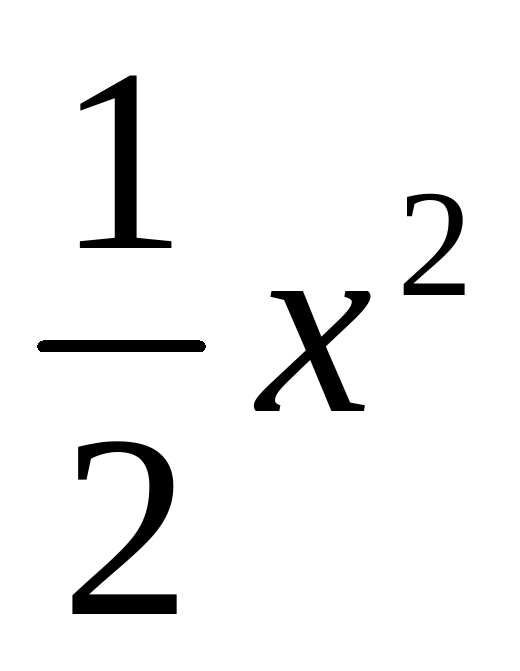 . Для того чтобы построить график мы на предыдущем уроке заполняли следующую таблицу.
. Для того чтобы построить график мы на предыдущем уроке заполняли следующую таблицу.
|
| х | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | | у | 8 | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 | 8 |
|
|
Построим график функции у = 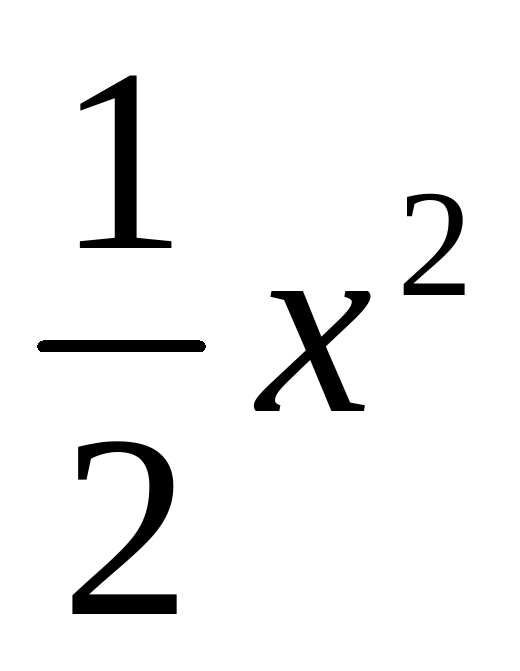 + 3. Для этого заполним таблицу:
+ 3. Для этого заполним таблицу:
|
| х | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | | у | 11 | 7,5 | 5 | 3,5 | 3 | 3,5 | 5 | 7,5 | 11 |
| Сравнивая формулы, получаем, что для заполнения таблицы достаточно к соответствующим значениям функции у = 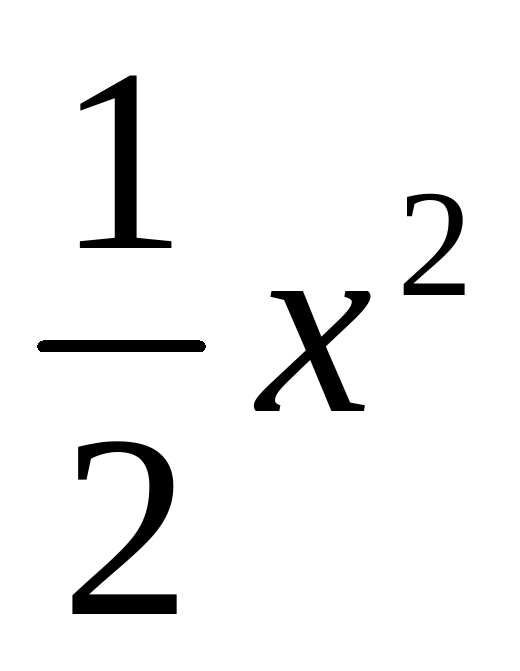 прибавить 3. прибавить 3. |
Значит для того, чтобы построить график функции у = 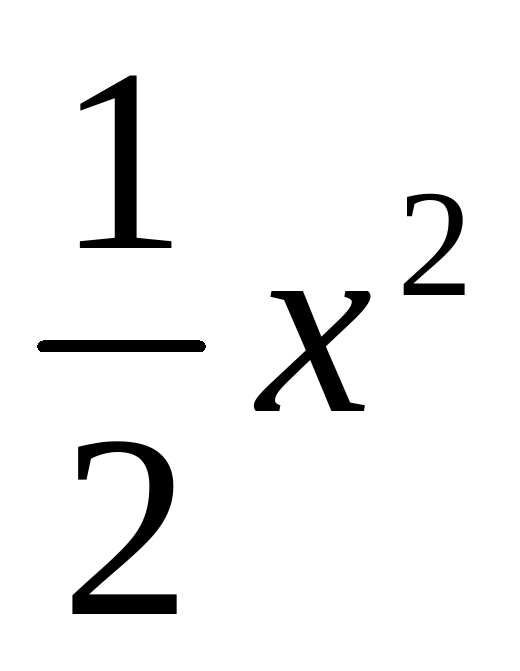 + 3, надо переместить каждую точку графика функции у =
+ 3, надо переместить каждую точку графика функции у = 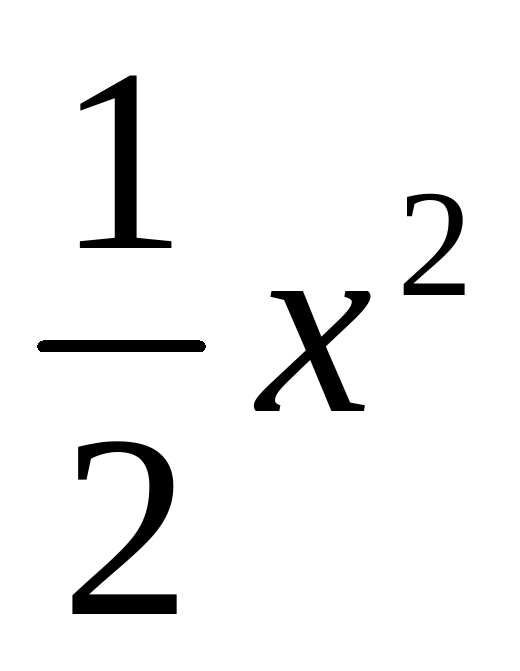 на 3 единицы вверх.
на 3 единицы вверх.
Вопрос. Как можно построить график функции у = 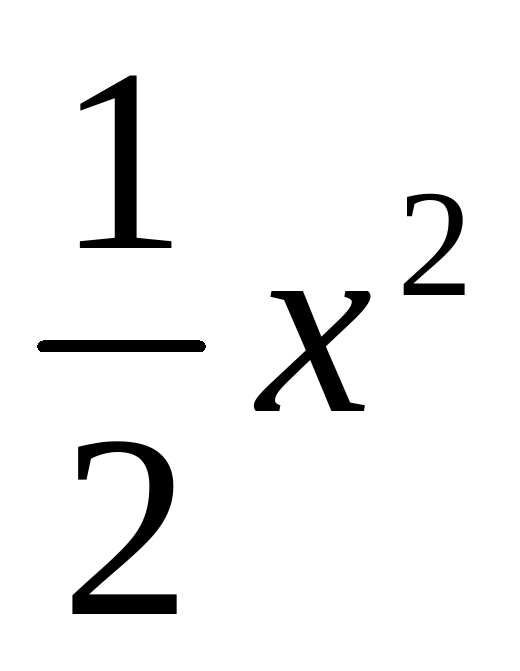 - 4?
- 4?
Построение графиков функций у = 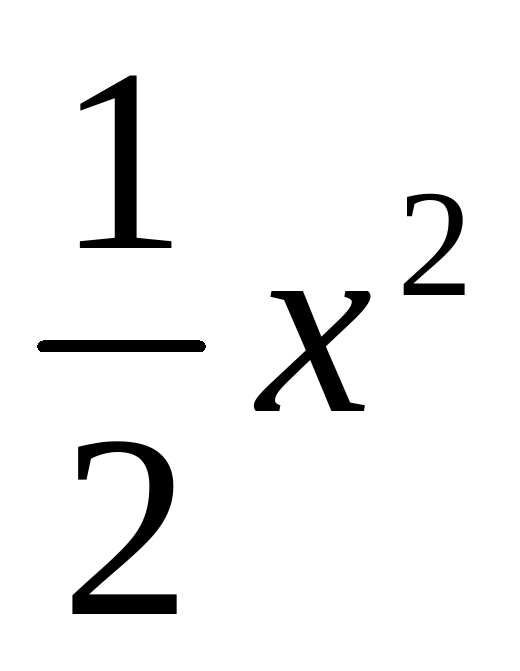 , у =
, у = 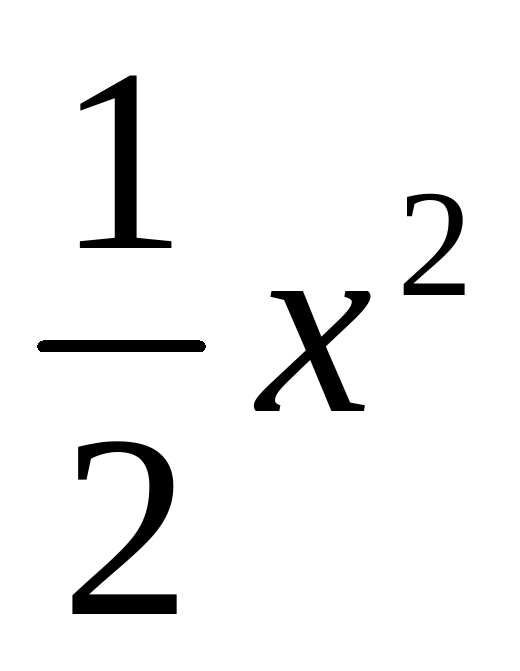 + 3, у =
+ 3, у = 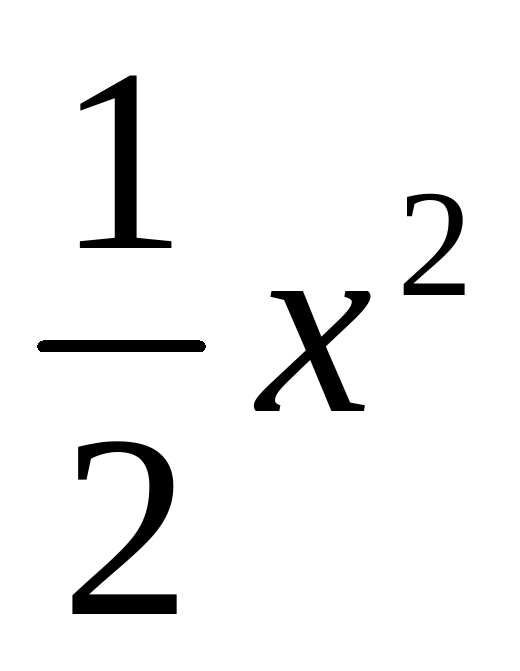 - 4 в одной системе координат, используя шаблоны.
- 4 в одной системе координат, используя шаблоны.
(Обсуждения и выводы)
Вывод. График функции у = ах2 + n является параболой, которую можно получить из графика функции
у = ах2 с помощью параллельного переноса вдоль оси у на n единиц вверх, если n0, или на 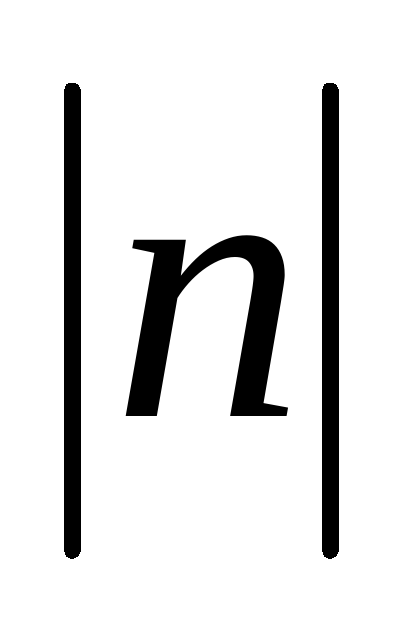 единиц вниз, если n
единиц вниз, если n
2) Рассмотрим функцию у = 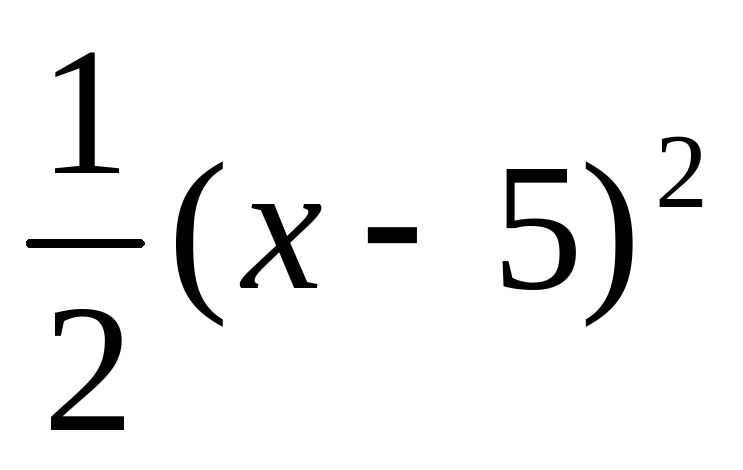 . Построим её график. Для чего составим таблицу значений функции, выбрав такие значения аргумента, которые на 5 больше соответствующих значений аргумента в таблице для функции у =
. Построим её график. Для чего составим таблицу значений функции, выбрав такие значения аргумента, которые на 5 больше соответствующих значений аргумента в таблице для функции у = 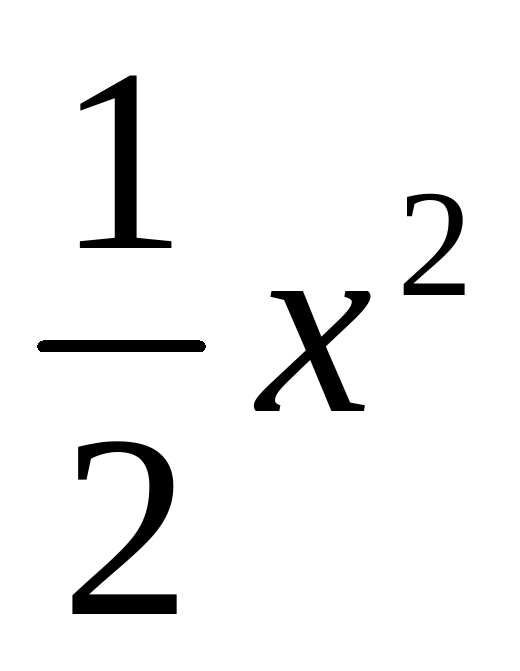
|
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | у | 8 | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 | 8 |
| Значения аргумента увеличились на 5, а значения функции остались прежними.
|
Значит для того, чтобы построить график функции у =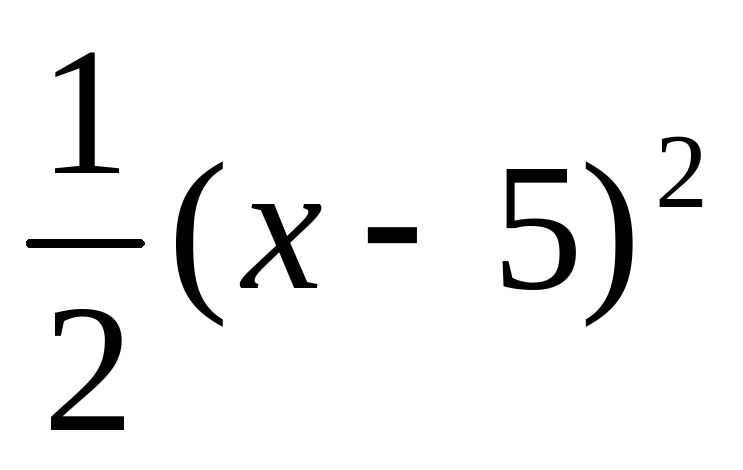 , надо переместить каждую точку графика функции у =
, надо переместить каждую точку графика функции у = 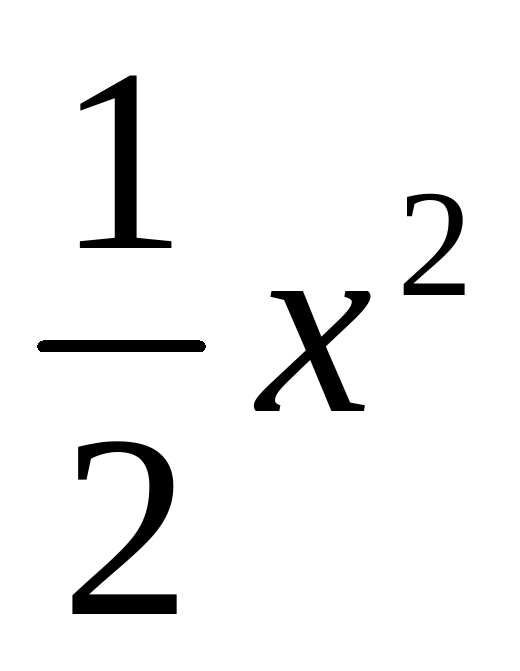 на 5 единицы вправо вдоль оси х.
на 5 единицы вправо вдоль оси х.
Вопрос. Как можно построить график функции у = ?
?
Построение графиков функций у = 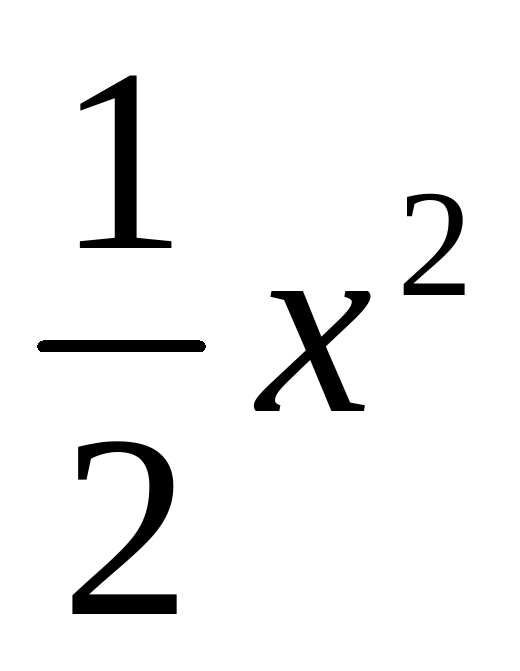 , у =
, у =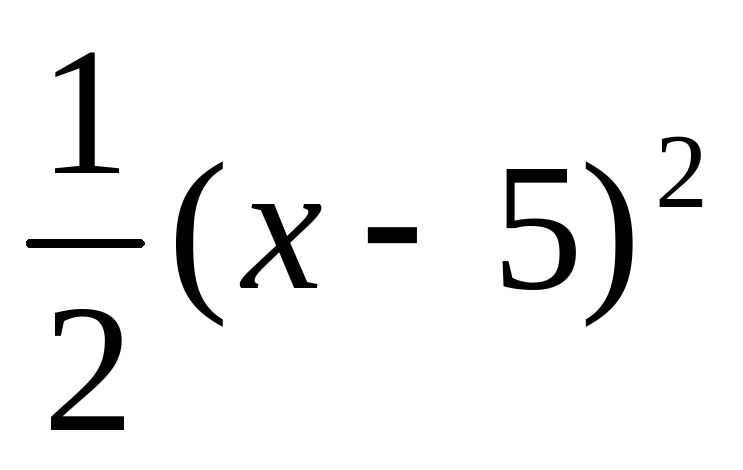 , у =
, у = в одной системе координат, используя шаблоны.
в одной системе координат, используя шаблоны.
(Обсуждения и выводы)
Вывод. График функции у = a (х - m)2 является параболой, которую можно получить из графика функции у = ах2 с помощью параллельного переноса вдоль оси х на m единиц вправо, если m0, или на  единиц влево, если m
единиц влево, если m
3)Вопрос. а)Как можно построить график функции у =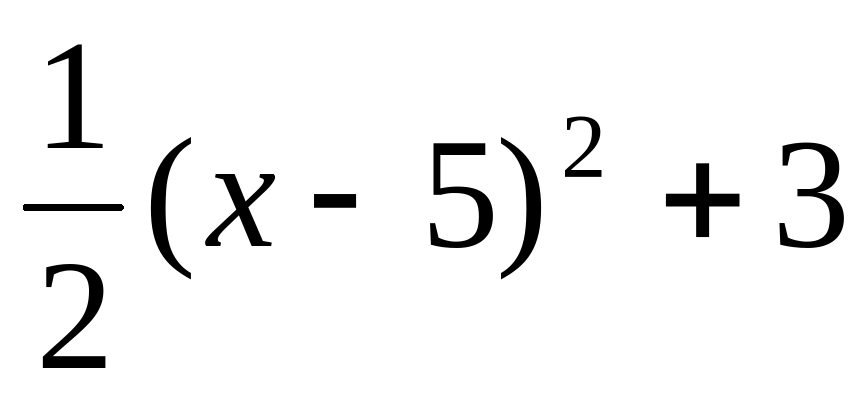 ?
?
б)Как можно построить график функции у =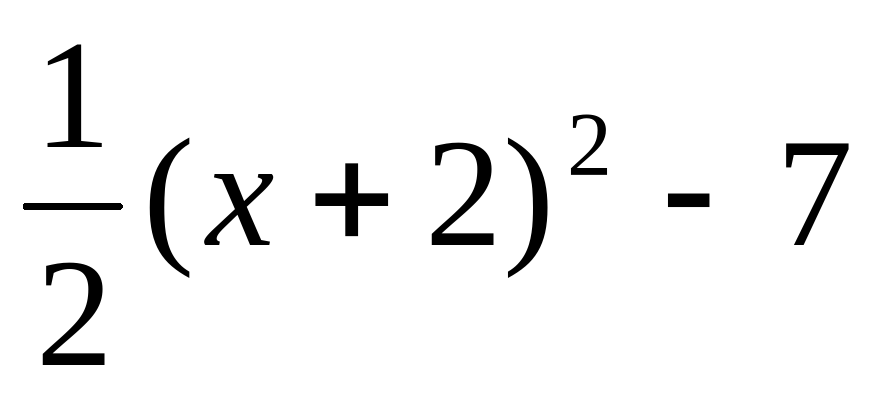 ?
?
Вывод. График функции у = a (х - m)2 + n является параболой, которую можно получить из графика функции у = ах2 с помощью двух параллельных переносов: параллельного переноса вдоль оси х на m единиц вправо, если m0, или на  единиц влево, если mn единиц вверх, если n0, или на
единиц влево, если mn единиц вверх, если n0, или на 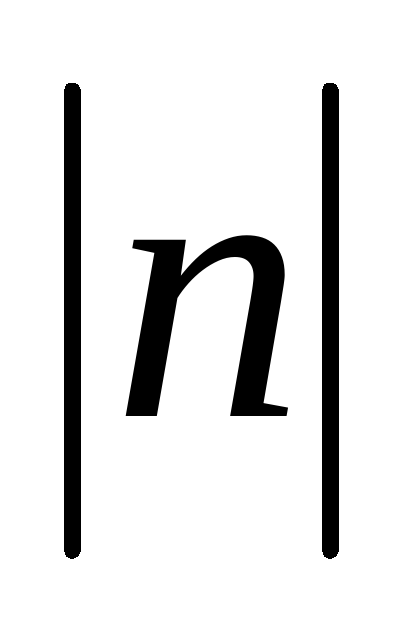 единиц вниз, если n
единиц вниз, если n
( на практике достаточно перемещать вершину параболы соответствующего шаблона в точку с координатами (m;n))
4) Полученные нами выводы о преобразовании графиков применимы к любым функциям.
График функции у = f(x) + n можно получить из графика функции у = f(x) с помощью параллельного переноса вдоль оси у на n единиц вверх, если n0, или на 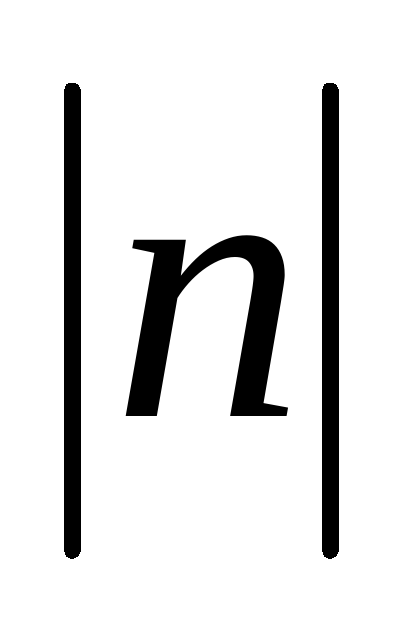 единиц вниз, если n
единиц вниз, если n
График функции у = f(x + m) можно получить из графика функции у = f(x) с помощью параллельного переноса вдоль оси х на m единиц вправо, если m0, или на  единиц влево, если m
единиц влево, если m
График функции у = f(x + m) + n можно получить из графика функции у = f(x) с помощью двух параллельных переносов:
1)параллельного переноса вдоль оси х на m единиц вправо, если m0, или на  единиц влево, если m
единиц влево, если m
2) с помощью параллельного переноса вдоль оси у на n единиц вверх, если n0, или на 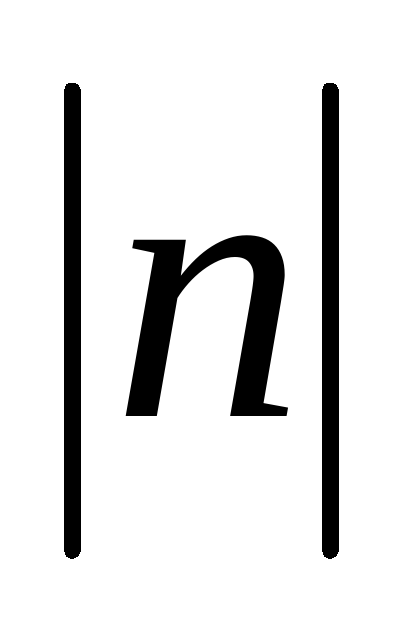 единиц вниз, если n
единиц вниз, если n
4) Обучающая самостоятельная работа.
Постройте в одной системе координат графики следующих функций, выбрав соответствующий шаблон.
а) у = х2 +1, в) у = , д) у = .
б) у = х2 - 3, г) у = ,
Проверить работу по готовым чертежам с помощью мультимедийного проектора.
4. Выполнение упражнений №108, 110(письменно), 116 (устно)
6. Д/з п.6, №107, 111,113, 235*.


















