
Графики кусочно – заданных функций
Мурзалиева Т.А. учитель математики МБОУ «Борская средняя общеобразовательная школа» Бокситогорский район Ленинградская область

Цель:
- освоить метод линейного сплайна для построения графиков, содержащих модуль;
- научиться применять его в простых ситуациях.

Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию.
Такие функции были известны математикам давно, начиная еще с Эйлера (1707-1783г.,швейцарский, немецкий и российский математик), но их интенсивное изучение началось, фактически, только в середине XX века.
В 1946 году Исаак Шёнберг (1903- 1990г., румынский и американский математик) впервые употребил этот термин. С 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании.

1 . Введение
2. Определение линейного сплайна
3. Определение модуля
4. Построение графиков
5. Практическая работа

Графики функций широко используются в различных областях инженерных знаний, поэтому умение строить, “читать”, прогнозировать их “поведение” имеют огромную роль в практической деятельности инженерных работников, метеорологов и людей других “математических” специальностей

Одно из основных назначений функций – описание реальных процессов, происходящих в природе.
Но издавна ученые – философы и естествоиспытатели выделяли два типа протекания процессов: постепенное ( непрерывное ) и скачкообразное.

При падении тела на землю сначала происходит непрерывное нарастание скорости движения , а в момент столкновения с поверхностью земли скорость изменяется скачкообразно , становясь равной нулю или меняя направление (знак) при «отскоке» тела от земли (например, если тело – мяч).
Но раз есть разрывные процессы, то необходимы средства их описаний. С этой целью вводятся в действие функции, имеющие разрывы .
 a - формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. " width="640"
a - формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. " width="640"
- Один из способов введения таких разрывов следующий:
Пусть функция y = f(x)
при x определена формулой y = g(x),
а при xa - формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет.
Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок;
если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной.
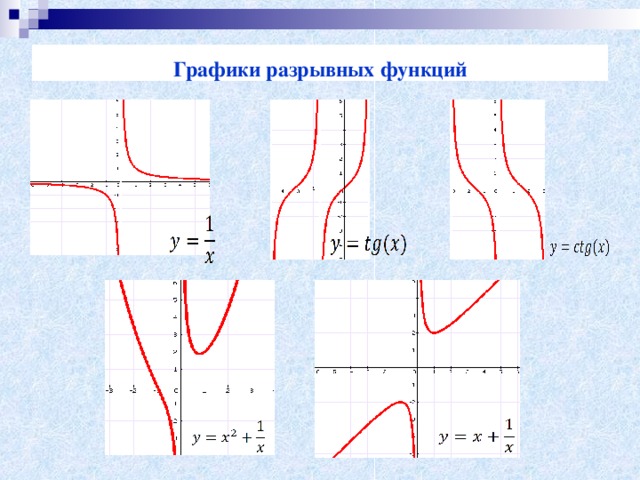
Графики разрывных функций
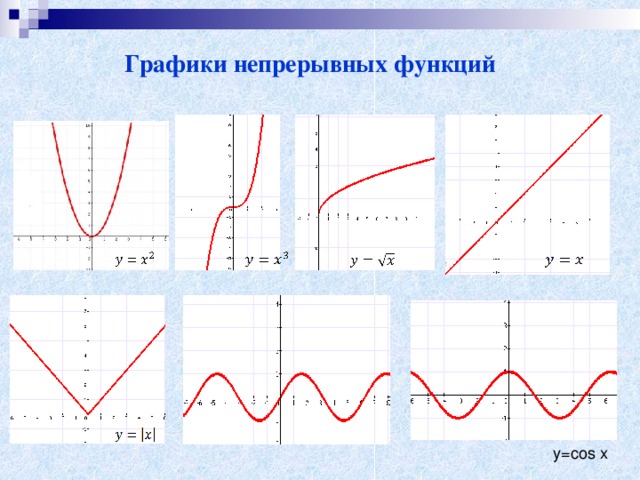
Графики непрерывных функций
y=cos x
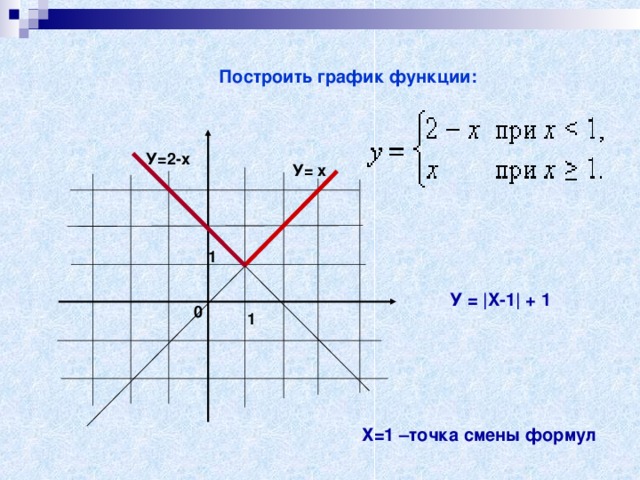
Построить график функции:
У=2-х
У= х
1
У = |X-1| + 1
0
1
Х=1 –точка смены формул

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера».
Модулем числа а называется расстояние ( в единичных отрезках ) от начала координат до точки А ( а) .
Это определение раскрывает геометрический смысл модуля.
Модулем ( абсолютной величиной ) действительного числа а называется то самое число а ≥ 0, и противоположное число –а , если а
А
а
х
0
 0 или х=0 у = -3х -2 при х " width="640"
0 или х=0 у = -3х -2 при х " width="640"
у
У=-3х-2
У=3х-2
х
-1
у
-2
1
4
х
0
у
1
-2
1
1
1
х
0
-2
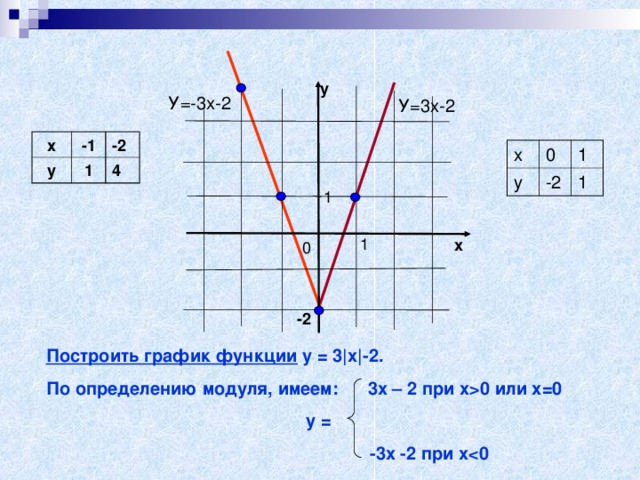
Построить график функции у = 3|х|-2.
По определению модуля, имеем: 3х – 2 при х0 или х=0
у =
-3х -2 при х
 x n ) " width="640"
x n ) " width="640"
. Пусть заданы х 1 х 2 х n – точки смены формул в кусочно-элементарных функциях.
Функция f, определенная при всех х, называется кусочно-линейной, если она линейна на каждом интервале
и к тому же выполнены условия согласования, то есть в точках смены формул функция не терпит разрыв.
Непрерывная кусочно-линейная функция называется линейным сплайном . Её график есть ломаная с двумя бесконечными крайними звеньями – левым (отвечающим значениям x n ) и правым ( отвечающим значениям x x n )
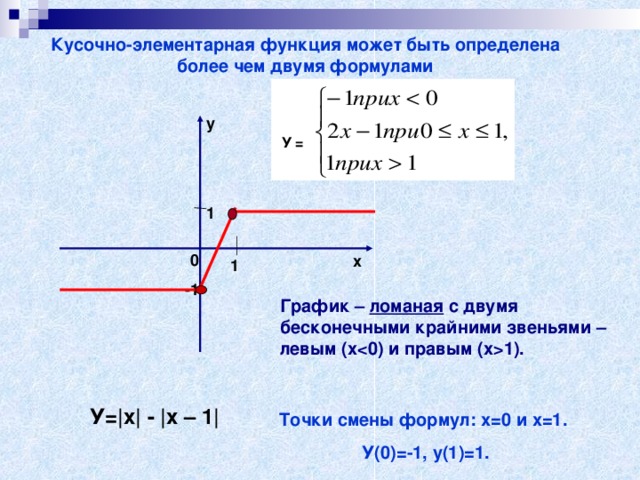
Кусочно-элементарная функция может быть определена более чем двумя формулами
у
У =
1
0
х
1
-1
График – ломаная с двумя бесконечными крайними звеньями – левым (х1).
У=|x| - |x – 1|
Точки смены формул: х=0 и х=1.
У(0)=-1, у(1)=1.

График кусочно-линейной функции удобно строить, указывая на координатной плоскости вершины ломаной.
Кроме построения n вершин следует построить также две точки : одну левее вершины A 1 ( x 1; y ( x 1)), другую – правее вершины An ( xn ; y ( xn )).
Заметим, что разрывную кусочно-линейную функцию нельзя представить в виде линейной комбинации модулей двучленов .

Построить график функции у = х+ |x -2| - |X|.
Непрерывная кусочно-линейная функция называется линейным сплайном
1.Точки смены формул: Х-2=0, Х=2 ; Х=0
у
2
2.Составим таблицу:
0
3
2
-1
х
1
0
2
1
у
0
х
2
У( 0 )= 0+|0-2|-|0|=0+2-0= 2 ;
у( 2 )=2+|2-2|-|2|=2+0-2= 0 ;
у (-1 )= -1+|-1-2| - |-1|= -1+3-1= 1 ;
у( 3 )=3+|3-2| - |3|=3+1-3= 1 .
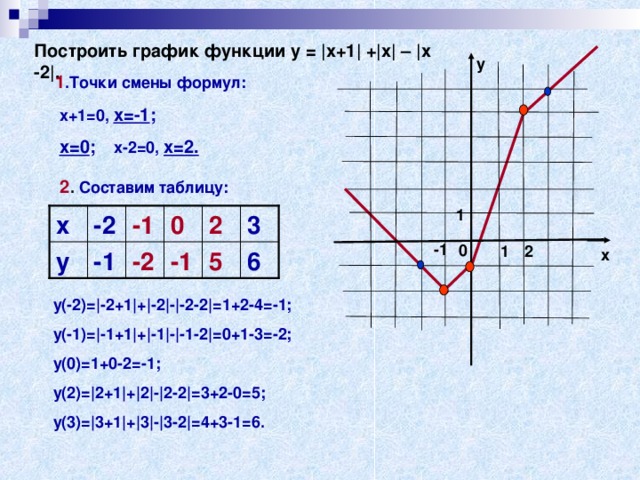
Построить график функции у = |х+1| +|х| – |х -2|.
у
1 .Точки смены формул:
х+1=0, х=-1 ;
х=0 ; х-2=0, х=2.
2 . Составим таблицу:
1
3
x
0
2
-2
-1
-1
0
2
1
x
у
-1
-2
-1
5
6
y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1;
y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2;
y(0)=1+0-2=-1;
y(2)=|2+1|+|2|-|2-2|=3+2-0=5;
y(3)=|3+1|+|3|-|3-2|=4+3-1=6.

|x – 1| = |x + 3|
Решите уравнение:
Решение. Рассмотрим функцию y = |x -1| - |x +3|
Построим график функции /методом линейного сплайна/
х -1 = 0, х = 1; х + 3 =0, х = - 3.
y
2. Составим таблицу:
- 4
х
-3
2
1
1
- 4
4
4
у
- 4
0
x
1
y(- 4) =|- 4–1| - |- 4+3| =|- 5| - | -1| = 5-1=4;
y( -3 )=|- 3-1| - |-3+3|=|-4| = 4;
y( 1 )=|1-1| - |1+3| = - 4 ;
y(-1) = 0.
y(2)=|2-1| - |2+3|=1 – 5 = - 4.
Ответ: -1.

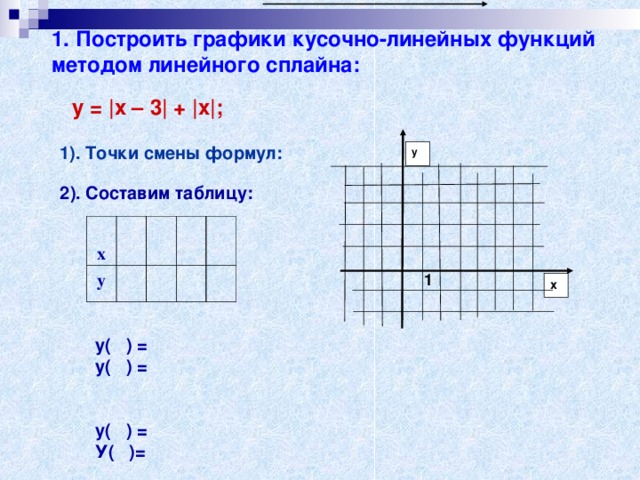
1. Построить графики кусочно-линейных функций методом линейного сплайна:
у = |x – 3| + |x|;
1). Точки смены формул:
у
2). Составим таблицу:
х
у
1
х
у( ) =
у( ) =
у( ) =
У( )=

2. Построить графики функций, используя УМК «Живая математика »
А) у = |2x – 4| + |x +1|
1) Точки смены формул:
2) y( ) =
y( ) =
y( ) =
у( ) =
Б) Постройте графики функций, установите закономерность :
a) у = |х – 4| б) y = |x| +1
y = |x + 3| y = |x| - 3
y = |x – 3| y = |x| - 5
y = |x + 4| y = |x| + 4
х
у
Используйте инструменты «Точка», «Отрезок», «Стрелка» на панели инструментов.
1. Меню «Графики».
2. Вкладка «Построить график».
.3. В окне «Калькулятор» задать формулу.

Постройте график функции:
1) У = 2х + 4
х
у
3) У =
х
у
2
4

1. Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006.
2. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011
3. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение , 2011
4. ВикипедиЯ свободная энциклопедия
http://ru.wikipedia.org/wiki/Spline














 a - формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. " width="640"
a - формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. " width="640"




 0 или х=0 у = -3х -2 при х " width="640"
0 или х=0 у = -3х -2 при х " width="640"
 x n ) " width="640"
x n ) " width="640"



















Электронная тетрадь по геометрии 9...
Геометрия 8 класс ФГОС
Алгебра 11 класc
Алгебра 10 класс
Геометрия 10 класс ФГОС
Математика. Вероятность и статистика. 7...
Алгебра 7 класс
Геометрия 9 класс ФГОС
© 2016, Мурзалиева Татьяна Александровна 10584 195
Рекомендуем курсы ПК и ППК для учителей