Алгоритм Евклида
Алгоритм Евклида позволяет находить наибольший общий делитель чисел, решать линейные уравнения в целых числах. Алгоритм основан на следующем факте: «Если при делении числа a на b получается остаток r, то НОД(a; b) = НОД(b; r)». Применение алгоритма Евклида заключается в последовательном делении с остатком. Сначала мы делим большее из двух чисел на меньшее. На каждом следующем шагу мы делим число, которое на предыдущем шагу было делителем, на число, которое на предыдущем шагу было остатком. Так поступаем до тех пор, пока не получим нулевой остаток. Это обязательно произойдёт через конечное число шагов, поскольку остатки всё время уменьшаются. Последний ненулевой остаток и будет наибольшим общим делителем исходных чисел. Отметим, что этот алгоритм может быть применён для нахождения наибольшего общего делителя не только чисел, но также многочленов и других объектов более общей природы.
Пример 1. Даны углы m и n , где m и n – взаимно простые целые числа. Построить угол 1.
Решение. Пусть при делении m на n получается частное q и остаток r. Вычитая q раз из угла m угол n, получим угол r . Аналогично мы можем получить все углы, градусная мера которых равна остаткам, возникающим при применении алгоритма Евклида к числам m и n. Поскольку m и n взаимно просты, последний из этих остатков – 1.
Пример 2. Докажите, что числа 2m−1 и 2n−1 взаимно просты тогда и только тогда, когда числа n и m взаимно просты.
Решение. Пусть n m. Обозначим F(n; m) = НОД(2n− 1; 2m − 1). Тогда
F(m; n) = НОД(2n − 1 − (2m − 1); 2m − 1) = НОД((2n−m−1)·2m; 2m−1) = НОД(2n−m−1; 2m−1) = F(n− m; n). Таким образом, пару чисел (m; n) можно заменить на пару (n − m; n). С помощью алгоритма Евклида мы придём к паре (d; 0), где d = НОД(m; n). Итак, НОД(2n−1; 2m−1) = НОД(2d−1; 20−1) = 2d−1. В нашем случае d = 1, 2d−1 = 1, поэтому числа 2n − 1 и
2m − 1 взаимно просты.
Задачи для самостоятельного решения
1. Решите уравнение в натуральных числах 7x − 11y = 1.
2. Разделить угол 19 на 19 равных частей.
3. Числа m и n – взаимно просты. Докажите, что уравнение mx + ny = 1 имеет решение в целых числах.
4. Докажите, что при любых целых неотрицательных m и n числа 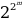 + 1 и
+ 1 и 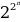 + 1 являются взаимно простыми.
+ 1 являются взаимно простыми.
5. Выведите из предыдущей задачи, что простых чисел бесконечно много.
6. Числа m и n нечётные. Докажите, что числа 2m + 1 и 2n + 1 взаимно просты тогда и только тогда, когда n и m взаимно просты.
7. Один прибор делает пометки на длинной ленте через каждые m см, другой – через каждые n см (m и n – взаимно простые). Верно ли, что какая-то синяя пометка окажется на расстоянии не большем 1 см от какой-то красной?
8. Периодическая последовательность имеет периоды m и n. Докажите, что
НОД(m; n) – тоже её период.
9. Разрешается сдвигать фишку вдоль числовой прямой на ±1 и на ± 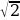 . Докажите, что из любого начального положения её можно придвинуть к началу координат ближе чем на 0,0001 .
. Докажите, что из любого начального положения её можно придвинуть к началу координат ближе чем на 0,0001 .
10. «Крокодилом» называется фигура, ход которой заключается в прыжке на клетку, в которую можно попасть сдвигом на одну клетку по вертикали или горизонтали, а затем на N клеток в перпендикулярном направлении (при N = 2 «крокодил» – это шахматный конь). При каких N «крокодил» может пройти с любой клетки бесконечной шахматной доски на любую другую?
11. Дан прямоугольник со сторонами 1 и α. От него отрезают квадрат, а с оставшимся прямоугольником проводят ту же процедуру. Рассматривается последовательность отношений сторон получившихся прямоугольников (большей к меньшей). Периодична ли эта последовательность, если число α равно
а) 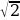 ; б)
; б) 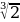 ; в)
; в) 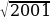 .
.
12. Словом называется последовательность букв, произведением uv двух слов u и v называется результат приписывания одного к другому. Докажите, что если uv = vu, то существует такое слово s и натуральные числа k и l, что u = sk , v = sl .
13. Решить уравнение в целых положительных числах
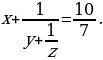







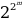 + 1 и
+ 1 и 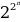 + 1 являются взаимно простыми.
+ 1 являются взаимно простыми. 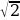 . Докажите, что из любого начального положения её можно придвинуть к началу координат ближе чем на 0,0001 .
. Докажите, что из любого начального положения её можно придвинуть к началу координат ближе чем на 0,0001 . 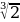 ; в)
; в) 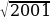 .
.