Идеи и методы решения нестандартных задач: графы

Графы

Во многих ситуациях удобно изображать объекты точками, а связи между ними – линиями или стрелками. Такой способ представления называется графом. Например, схема метро – это граф. Точки называют вершинами графа, а линии – ребрами. Вершину называют чётной, если из неё выходит чётное число рёбер и нечётной в противном случае. Граф называют связным, если между любыми вершинами существует путь, состоящий из рёбер графа, ориентированным – если на каждом ребре указано направление, плоским – если он нарисован на плоскости и его ребра не пересекаются (во внутренних точках). При решении многих олимпиадных задач используются следующие утверждения, относящиеся к обходу рёбер графа:

1) если в графе больше двух нечётных вершин, то его правильный обход (т. е. обход, при котором каждое ребро проходится ровно один раз) невозможен;

2) для всякого чётного связного графа существует правильный обход, который можно начать с любой вершины и который обязательно кончается в той же вершине, с которой начался;

3) если в связном графе ровно две нечётные вершины, то существует правильный обход, причём в одной из них он начинается, а в другой – кончается;

4) в любом графе количество нечётных вершин чётно.

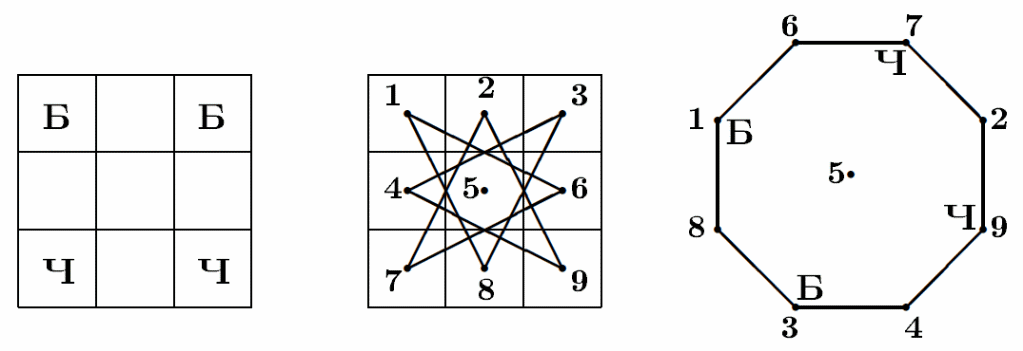
Пример 1. В углах шахматной доски 3 × 3 стоят 4 коня: 2 белых (в соседних углах) и два чёрных. Можно ли за несколько ходов (по шахматным правилам) поставить коней так, чтобы во всех соседних углах стояли кони разного цвета?

Решение. Отметим центры клеток доски и соединим отрезками пары отмеченных точек, если из одной в другую можно пройти ходом коня. Мы получим граф, содержащий «цикл» из восьми точек и одну изолированную точку (рис. ниже). Перемещение коней по доске соответствует движению по ребрам этого цикла. Ясно, что при движении по циклу нельзя изменить порядок следования коней.

Пример 2. Выпишите в ряд цифры от 1 до 9 так, чтобы число, составленное из двух соседних цифр, делилось либо на 7, либо на 13.

Решение. Напишем цифры на листе. Соединим стрелками те цифры, которые могут следовать друг за другом.

Теперь ясно, что первой идёт 7, затем 8 и 4. Уберём «лишние» стрелки, ведущие в уже использованные цифры 8 и 4.

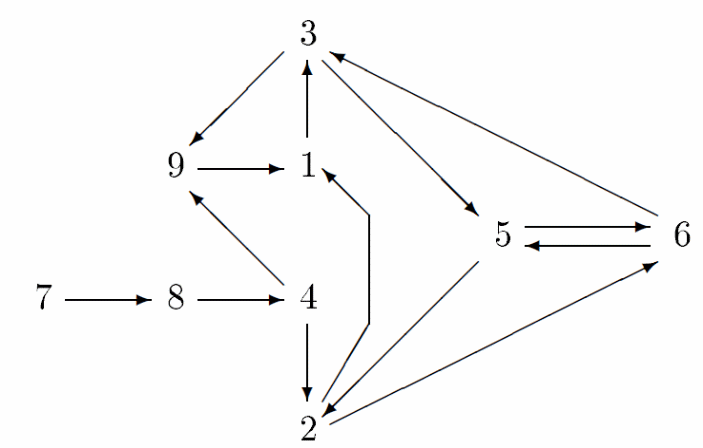
Если из 4 пойти в 2, то несложным перебором убедимся, что этот путь тупиковый. Значит, после 4 идёт 9. Дальше идёт 1, и остаток пути определяется однозначно.

Ответ: 784913526.

Пример 3. В стране Радонежии некоторые города связаны между собой авиалиниями. Из столицы выходит 1985 авиалиний, из города Дальнего – одна, а из остальных городов – по 20 линий. Докажите, что из столицы можно добраться до Дальнего (быть может, с пересадками).

Решение. Рассмотрим множество городов, до которых можно добраться из столицы. Это граф: его вершины – города, ребра – авиалинии, их соединяющие. Из каждой вершины графа выходит столько рёбер, сколько всего авиалиний выходит из соответствующего города. Граф содержит нечётную вершину – столицу. Поскольку число нечётных вершин в графе чётно, в нем есть ещё одна нечётная вершина. Этой вершиной может быть только город Дальний.

Задачи для самостоятельного решения

1. Расположите на плоскости 6 точек и соедините их непересекающимися линиями так, чтобы из каждой точки выходили четыре линии.

2. В трёх вершинах правильного пятиугольника расположили по фишке. Разрешается передвигать их по диагонали в любую свободную вершину. Можно ли таким образом добиться того, чтобы одна из фишек вернулась на свое место, а две другие поменялись местами?

3. В марсианском метро 100 станций. От любой станции до любой другой можно проехать. Забастовочный комитет хочет закрыть проезд через одну из станций так, чтобы между всеми остальными станциями был возможен проезд. Докажите, что такая станция найдётся.

4. На математической олимпиаде было предложено 20 задач. На закрытие пришло 20 школьников. Каждый из них решил по две задачи, причём выяснилось, что среди пришедших каждую задачу решило ровно два школьника. Докажите, что можно так организовать разбор задач, чтобы каждый школьник рассказал одну из решенных им задач, и все задачи были разобраны.

5. Докажите, что в плоском графе найдётся вершина, из которой выходит не более 5 рёбер.

6. а) Вершины плоского графа можно раскрасить в 6 цветов так, чтобы вершины, соединённые ребром, имели разный цвет.

б) Конечная плоская карта допускает раскраску в 6 цветов такую, что соседние страны будут окрашены в разные цвета.

Указание. а) Воспользуйтесь результатом предыдущей задачи – найдите вершину, из которой выходит не более 5 рёбер. Далее примените индукцию – если удалось покрасить все вершины, кроме этой одной, то и для неё цвет найдётся.

7. В спортклубе тренируются 100 толстяков, веса которых равны 1 кг, 2 кг, . . . , 100 кг. На какое наименьшее число команд их можно разделить, чтобы ни в какой команде не было двух толстяков, один из которых вдвое тяжелее другого?

8. Клетчатая плоскость раскрашена десятью красками так, что соседние (т. е. имеющие общую сторону) клетки покрашены в разные цвета, причём все десять красок использованы. Каково минимально возможное число пар соседних красок? (Две краски называются соседними, если ими покрашены какие-то две соседние клетки.)

9. В тридевятом царстве каждые два города соединены дорогой с односторонним движением. Докажите, что существует город, из которого можно проехать в любой другой не более чем по двум дорогам.

10. В городе на каждом перекрестке сходится чётное число улиц. Известно, что с любой улицы города можно проехать на любую другую. Докажите, что все улицы города можно объехать, побывав на каждой по одному разу.

11. Последовательность из 36 нулей и единиц начинается с пяти нулей. Среди пятёрок подряд стоящих цифр встречаются все 32 возможные комбинации. Найдите пять последних цифр последовательности.

12. Дан правильный 45-угольник. Можно ли так расставить в его вершинах цифры от 0 до 9 так, чтобы для любой пары различных цифр нашлась сторона, концы которой занумерованы этими цифрами.

Указание. Рассмотреть полный граф, вершины которого суть цифры от 0 до 9. Задача сводится к его обходу.

13. Докажите, что можно расположить по кругу символы 0 и 1 так, чтобы любой возможный набор из n символов, идущих подряд, встретился один раз.

Указание. Рассмотреть граф, вершины которого суть слова длины n − 1. Две вершины u и v соединяются стрелкой, если существует слово длины n, у которого u является началом, а v – концом.

14. Рёбра дерева окрашены в два цвета. Если в какую-то вершину приходят рёбра только одного цвета, то их все можно перекрасить в другой цвет. Можно ли все дерево сделать одноцветным?

15. Докажите, что количество вершин любого дерева на единицу больше количества его рёбер.