Индукция
Метод доказательства утверждений типа: «Для каждого натурального n верно, что . . . ». Такое утверждение можно рассматривать как цепочку утверждений: «Для n = 1 верно, что . . . », «Для n = 2 верно, что. . . » и т. д.
Первое утверждение цепочки называется базой (или основанием) индукции. Его обычно легко проверить. Затем доказывается шаг индукции: «Если верно утверждение с номером n, то верно утверждение с номером (n+1)». Шаг индукции также можно рассматривать как цепочку переходов: «Если верно утверждение 1, то верно утверждение 2», «Если верно утверждение 2, то верно утверждение 3» и т. д.
Если верна база индукции, и верен шаг индукции, то все утверждения верны (это принцип математической индукции).
Иногда для доказательства очередного утверждения цепочки надо опираться на все предыдущие утверждения. Тогда индуктивный переход звучит так: «Если верны все утверждения с номерами от 1 до n, то верно утверждение с номером (n + 1)».
Бывает удобен индуктивный спуск или «обратная индукция» – если утверждение с номером n (n 1) можно свести к одному или нескольким утверждениям с меньшими номерами и первое утверждение верно, то все утверждения верны.
Пример 1. Докажите, что число состоящее из 243 единиц, делится на 243.
Решение. Заметим, что 243 = 35 . Попробуем доказать более общее утверждение, что число, составленное из 3n единиц, делится на 3n. Оказывается, это проще.
Для n = 1 утверждение верно (111 делится на 3).
Заметим, что 111111111 = 111 · 1001001, и вообще число из 3n единиц разлагается на множители:
1
 . . . 1 = 1 . . . 1 · 10 . . . 010 . . . 01
. . . 1 = 1 . . . 1 · 10 . . . 010 . . . 01


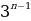


причём, второй множитель делится на 3 (по признаку делимости на 3). Итак, в последовательности чисел 111, 111111111, . . . , «3
n единиц» каждое следующее равно предыдущему, умноженному на число, кратное трём. Поэтому, если
1 . . . 1 делится на 3
n−1 , то 1 . . . 1 делится на 3
n.
Теперь индукция очевидна.
Замечание. Мы специально не произносили слов «база индукции» и «шаг индукции», чтобы не отвлекать внимание от более существенных моментов.
Пример 2. На плоскости провели несколько прямых и окружностей. Докажите, что части на которые разбита плоскость, можно раскрасить в два цвета так, чтобы соседние части (граничащие по отрезку или дуге) были покрашены в разные цвета.
Решение. Сначала сотрём все прямые и окружности, но запомним, где они находились. Покрасим всю плоскость в один цвет, а потом будем восстанавливать границы, перекрашивая при этом части, на которые они делят плоскость. Каждый раз, добавляя прямую, мы перекрашиваем в противоположный цвет все части, лежащие по одну её сторону, и оставляем без изменения части, лежащие по другую сторону. Добавляя окружность, мы перекрашиваем все части, лежащие внутри неё и оставляем без изменения, лежащие снаружи. Таким образом, каждый участок любой из нарисованных линий будет являться границей двух областей разного цвета.
Пример 3. Докажите, что если 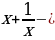 целое, то
целое, то 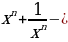 тоже целое.
тоже целое.
Решение. Пусть  . Заметим, что T0 = 2 и T1 =
. Заметим, что T0 = 2 и T1 = 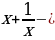 целые. Рассмотрим произведение
целые. Рассмотрим произведение 
Отсюда  целое. Обобщим идею и рассмотрим произведение
целое. Обобщим идею и рассмотрим произведение 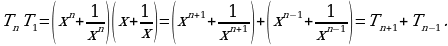
Отсюда получим, что 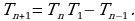 Поэтому, если
Поэтому, если 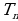 и
и 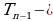 целые числа, то
целые числа, то  тоже целое. Теперь по индукции получим, что
тоже целое. Теперь по индукции получим, что  целое при всех n.
целое при всех n.
Пример 4. Пятеро разбойников добыли мешок золотого песка. Они хотят поделить его так, чтобы каждый был уверен, что он получил не меньше одной пятой золота. Никаких способов измерения у них нет, однако каждый умеет оценивать на глаз величину кучи песка. Мнения разбойников о величине куч могут расходиться. Как им поделить добычу?
Решение. Первый способ. Пусть сначала два разбойника поделят добычу между собой: один поделит песок на две равные, по его мнению, кучи, а второй выберет себе кучу. Затем каждый из них поделит свою кучу на три равные, по его мнению, кучи, а третий возьмёт у каждого по одной куче. Затем эти трое делят свои кучи на четыре равные, по их мнению, части, а четвёртый разбойник возьмёт у каждого по одной куче. Аналогично для пятого разбойника.
Второй способ. Найдём «самого скромного» разбойника и отдадим ему его долю. Для этого попросим первого разбойника отделить 1/5 часть мешка и спросим второго разбойника о размере отделённой части: если он считает, что она больше 1/5, то пусть уменьшит ее до 1/5, а если считает, что она не больше 1/5, то позовём третьего разбойника и повторим процедуру. В итоге отдадим кучу тому, кто последним к ней приложил руку. Среди оставшихся разбойников опять найдём самого скромного и отдадим ему полученную кучу и т. д.
Пример 5. Докажите, что нельзя построить правильный 7-угольник с вершинами в целочисленной решетке.
Решение. Допустим, что это возможно. Заметим, что сторона 7-угольника меньше радиуса описанной около него окружности. Сделаем параллельный перенос всех сторон 7-угольника в одну точку. Получим «ёжик». Соединив концы «иголок ёжика», получим новый правильный 7-угольник с вершинами в целых точках, но меньшего размера. Но 7-угольники с вершинами в целых точках нельзя уменьшать до бесконечности. Противоречие. Значит, такой 7-угольник построить нельзя.
Задачи для самостоятельного решения
1. Докажите, что любое число рублей большее семи можно разменять трёшками и пятёрками. (Трёшками и пятёрками называются купюры в 3 и 5 рублей соответственно, которые находились в обращении в Советском Союзе до 1991 года).
2. Несколько прямых делят плоскость на части. Каждая прямая «заштрихована» с одной стороны. Докажите, что у одной из частей все границы «заштрихованы» изнутри.
3. Из квадрата 128×128 вырезали одну клетку. Докажите, что эту фигуру можно замостить уголками из трёх клеток.
4. Докажите, что простых чисел бесконечно много.
5. Для любого натурального k докажите неравенство 2k k.
6. Докажите неравенство Коши:
 где
где 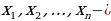 неотрицательные числа.
неотрицательные числа.
Указание. Используйте более сложную схему индукции по количеству переменных: сначала по степеням двойки, потом от степени двойки к меньшему числу.
7. Четыре одинаковые банки наполнены красками на три четверти; цвета всех красок различны. Имеется возможность переливать любую часть жидкости из одной банки в другую. Можно ли во всех банках сделать одинаковую смесь? (Другой посуды нет, выливать краску нельзя.)
8. В городе N домов. Какое наибольшее число заборов можно построить в этом городе, если 1) заборы не пересекаются, 2) каждый забор огораживает хотя бы один дом, 3) никакие два забора не огораживают одну и ту же совокупность домов?
9. Докажите, что предпоследняя цифра десятичной записи любой степени тройки чётна.
10. Для любого x −1 и натурального n докажите неравенство Бернулли:
(1 + x) n 1 + nx:
11. Ханойская башня. Головоломка «Ханойская башня» представляет собой три штырька, на один из которых нанизаны семь колец убывающих размеров, как показано на рис. ниже. Разрешается снимать по одному кольцу с любого штырька и нанизывать его на любой другой штырёк, но при этом запрещается класть большее кольцо поверх меньшего. Можно ли, соблюдая эти правила, переложить все кольца на другой штырёк? 









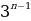

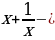 целое, то
целое, то 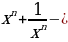 тоже целое.
тоже целое.  . Заметим, что T0 = 2 и T1 =
. Заметим, что T0 = 2 и T1 = 
 целое. Обобщим идею и рассмотрим произведение
целое. Обобщим идею и рассмотрим произведение 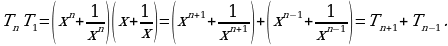
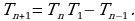 Поэтому, если
Поэтому, если 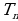 и
и 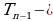 целые числа, то
целые числа, то  тоже целое. Теперь по индукции получим, что
тоже целое. Теперь по индукции получим, что  целое при всех n.
целое при всех n. где
где 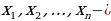 неотрицательные числа.
неотрицательные числа. 

















