Идеи и методы решения нестандартных задач: подсчёт двумя способами

Подсчёт двумя способами

При составлении уравнений выражают некоторую величину двумя способами (например, площадь, путь или время). Иногда некоторую величину оценивают двумя способами, тогда получают или неравенство, или величины разной чётности.

Пример 1. Можно ли расставить числа в квадратной таблице 5×5 так, чтобы сумма чисел в каждой строке была положительной, а в каждом столбце отрицательной?

Решение. Допустим, что можно. Найдем сумму всех чисел. Если считать её по строкам, то сумма будет положительной, а если по столбцам – то отрицательной. Противоречие. Значит, так расставить числа нельзя.

Пример 2. В классе 27 человек. Каждый мальчик дружит с четырьмя девочками, а каждая девочка – с пятью мальчиками. Сколько в классе мальчиков и сколько девочек?

Решение. Пусть m – число мальчиков, d – число девочек. Найдем общее количество «дружб» двумя способами. Поскольку каждый мальчик дружит с четырьмя девочками, это число равно 4m. С другой стороны, каждая девочка дружит с пятью мальчиками, значит это число равно 5d. Получаем уравнение 4m = 5d. Поскольку m + d = 27, то m = 15, d = 12.

Ответ: 15 мальчиков, 12 девочек.

Пример 3. Найдите сумму геометрической прогрессии S_n = 1 + 3 + 9 + … + 3ⁿ.

Решение. Заметим, что зная S_n, можно получить следующую сумму S_n+1 двумя способами: либо добавить 3ⁿ⁺¹, либо умножить все слагаемые на 3, а потом прибавить 1. Получаем уравнение: S_n+3ⁿ⁺¹ = 3·Sn+1. Отсюда .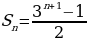

Пример 4. Докажите, что медианы треугольника пересекаются в одной точке.

Решение. Пусть AA₁, BB₁ и CC₁ – медианы треугольника ABC, O – точка пересечения медиан AA₁ и CC₁. Проведём отрезки BO и OB₁. Обозначим площади шести треугольников, на которые разбился треугольник ABC как на рисунке ниже.

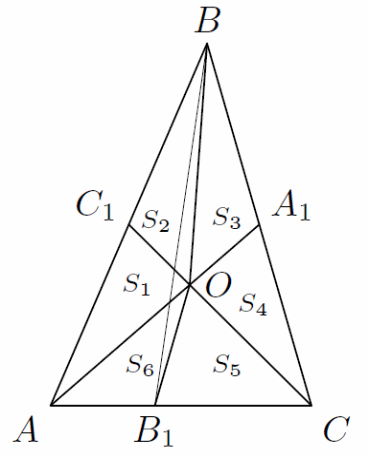
Воспользуемся тем, что медиана делит треугольник на два равновеликих треугольника. Действительно, у этих треугольников равны основания и общая высота. Поэтому S₁ = S₂, S₃ = S₄, S₅ = S₆. Кроме того треугольники ACC₁ и CAA₁ равновелики, поскольку площадь каждого из них составляет половину площади исходного треугольника ABC. Выбрасывая из них общую часть – треугольник AOC, получаем равновеликость треугольников AOC₁ и COA₁, т. е. S₁ = S₄. Следовательно,
S₆ + 2S₁ = S₅ + 2S₄, значит четырёхугольники ABOB₁ и CBOB₁ равновелики. С другой стороны, медиана BB₁ тоже делит ABC на две равновеликие части, поэтому точка O должна лежать на отрезке BB₁.

Пример 5. Могут ли все грани выпуклого многогранника иметь 6 и более сторон?

Решение. Нет, не могут. Оценим двумя способами среднее арифметическое всех углов всех граней. С одной стороны, среднее арифметическое углов n-угольника при n  6 не меньше 120. С другой стороны, к каждой вершине многогранника примыкают не менее трёх граней, и сумма примыкающих углов строго меньше 360. Поэтому среднее арифметическое углов при каждой вершине строго меньше 120. Полученное противоречие доказывает, что такого многогранника не существует.

Задачи для самостоятельного решения

1. Можно ли соединить 5 городов дорогами так, чтобы каждый город был соединён с тремя другими?

2. В каждой клетке прямоугольной таблицы размером m×k клеток написано число. Сумма чисел в каждой строке и в каждом столбце равна 1. Докажите, что m = k.

3. Существует ли выпуклый 1978-угольник, все углы которого выражаются целым числом градусов?

4. Найдите сумму коэффициентов многочлена (x³ − x + 1)¹⁰⁰.

5. Докажите, что не существует многогранника, у которого

а) все грани – шестиугольники;

б) в каждой вершине сходятся 6 граней.

6. Треугольник разрезали на выпуклые четырёхугольники. Докажите, что хотя бы у одного четырёхугольника есть угол не меньше 120.

7. В городе отличников от каждой площади отходит ровно 5 улиц. Докажите, что число площадей чётно, а число улиц делится на 5 (улица соединяет две площади).

8. В квадрате со стороной единица поместили несколько отрезков, параллельных сторонам квадрата (квадрату принадлежит граница, а отрезкам принадлежат концы). Отрезки могут пересекать друг друга. Сумма их длин равна 18. Докажите, что среди частей, на которые квадрат разбит объединением отрезков, найдётся такая, площадь которой не меньше 0,01.

Указание. Оцените двумя способами сумму периметров частей. Чем меньше площадь, тем относительно больший периметр на неё приходится.

9. Четыре кузнечика сидят в вершинах квадрата. Каждую минуту один из них прыгает в точку, симметричную относительно другого кузнечика. Докажите, что кузнечики не могут одновременно оказаться в вершинах квадрата большего размера.
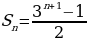