Индивидуальный итоговый проект на тему «Удивительный мир флексагонов» по учебному предмету «Геометри\

Муниципальное казённое общеобразовательное учреждение

«Новокасторенская средняя общеобразовательная школа»

Касторенского района Курской области

ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ

на тему «Удивительный мир флексагонов»

по учебному предмету «Геометрия»

Обучающийся: Василенко Александр Класс 9

Руководитель проекта: И.Н. Гордеева, учитель математики

п. Новокасторное – 2020

Содержание

Стр.

Введение………………………………………………………………………

Глава I. Удивительный мир флексагонов

1. Что такое флексагон?…………………………………………………4

2. История открытия ……………………………………………………5

3. Виды флексагонов и их свойства…..……………………………….7

4. Методы складывания флексагонов ………………………………..11

Глава II. Флексагоны, как средство математического моделирования

2.1. Мастер – класс по складыванию тригексафлексагона…………….12

2.2. Применение флексагонов ……………………………………….......13

Заключение………………………………………………………………..14

Список информационных источников………………………………….15

Введение

Актуальность работы: складывание флексогонов может оказаться полезным и занимательным хобби и времяпровождением, позволяющее изучить геометрические свойства этих фигур, развить пространственное воображение и совершенствовать мелкую моторику рук. Кроме того, знакомство с флексагонами позволит по-новому взглянуть на мир математики и внести разнообразие в привычные окружающие нас предметы быта и интерьера.

Гипотеза: Флексагоны - это не просто игрушка или обычное оригами, а занимательная математическая головоломка.

Объект исследования: различные виды флексагонов.

Предмет исследования: история возникновения флексагонов, способы конструирования, применение.

Цель исследования: проведение анализа имеющейся информации о флексагонах и освоение методик складывания простейших флексагонов.

Задачи исследования:

•  познакомиться со специальной литературой, раскрыть содержание понятия «флексагон»;

•  создать модели простейших флексагонов;

•  выявить области применения флексагонов в жизни человека;

Методы исследования:

• сбор информации, анализ периодической и научной литературы;

• точные расчёты при построении;

• создание наглядных моделей.

Практическая значимость.

Практическая значимость данной работы заключается в возможности построения разнообразных моделей флексагонов из любых материалов и для любых предметов, с которыми сталкивается человек в повседневной жизни.

Глава I. Удивительный мир флексагонов

1. Что такое флексагон?

Флексагоны – это многоугольники, сложенные из полосок бумаги прямоугольной или более сложной, изогнутой формы, которые обладают удивительным свойством: при перегибании флексагонов их наружные поверхности прячутся внутрь, а ранее скрытые поверхности неожиданно выходят наружу. Происходит это слово от английского to flex, что означает «складываться, гнуться». Если бы не одно случайное обстоятельство – различие в формате английских и американских блокнотов, – флексагоны, возможно, не были бы открыты и по сей день и многие выдающиеся математики лишились бы удовольствия изучать их замысловатую структуру.

Флексагон – это математическая головоломка. Очень увлекательная, забавная игрушка, обладающая удивительными свойствами.

Флексор – вращающиеся кольца тетраэдров.  Эта цепочка из тетраэдров обладает удивительной способностью изгибаться и выворачиваться до бесконечности, все время, меняя свою форму. Кольцо из тетраэдров – это первый пример флексора – изгибаемого многогранника.

Рис.1.

1. История открытия

В конце 1939 года Артур Стоун, 23 летний аспирант из Англии, изучавший математику в Принстоне, обрезал листы американского блокнота, чтобы подогнать их под привычный формат. Желая немного развлечься, Стоун принялся складывать из отрезанных полосок бумаги различные фигуры. Одна из сделанных им фигур оказалась особенной интересной. Перегнув полоску бумаги в трех местах и соединив концы, он получил правильный шестиугольник. Взяв этот шестиугольник за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Если бы обе стороны исходного шестиугольника были бы разного цвета, то после перегибания видимая поверхность изменила бы свою окраску. Так был открыт самый первый флексагон с тремя поверхностями. Поразмыслив над ним ночь, Стоун наутро убедился в правильности своих чисто умозрительных заключений: оказалось, можно построить и более сложный шестиугольник с шестью поверхностями вместо трех. Эта модель показалась Стоуну настолько интересной, что он решил показать её своим друзьям по университету. Вскоре был создан «Флексагонный комитет», куда вошли сам Стоун, аспирант-математик Бриан Таккерман, аспирант-физик Ричард Фейнман и молодой преподаватель математики Джон У.Тьюки. Комитет обнаружил, что можно сделать флексагоны с 9, 12, 15 и большим числом поверхностей. Таккерману удалось сделать действующую модель флексатона с 48 поверхностями. Он также обнаружил, что из зигзагообразной полоски бумаги можно сложить тетрагексафлексагон (с четырьмя) и пентагексафлексагон (с пятью поверхностями). Вообще один вид флексагона можно складывать по-разному. Так, гексагексафлексагон можно сложить тремя способами, а декагексафлексагон - 82 способами… https://school-science.ru/2/7/30072

Артур Стоун с друзьями посвятили много времени складыванию этих четырёхсторонних разновидностей флексагонов, но им так и не удалось построить полную теорию, охватывающую все, на первый взгляд ничем не связанные, разновидности этих головоломок. Конструкция тетрафлексагонов используется в шарнирных соединениях «двойного действия» – устройствах, с одинаковой лёгкостью открывающихся в обе стороны. Эту же конструкцию можно обнаружить и в детских игрушках.

Рис.2. Артур Х. Стоун

с тремя поверхностями, изобретенный Артуром Стоуном, складывается из прямой полоски бумаги, поделенной на 10 равносторонних треугольников (один служит для склейки).

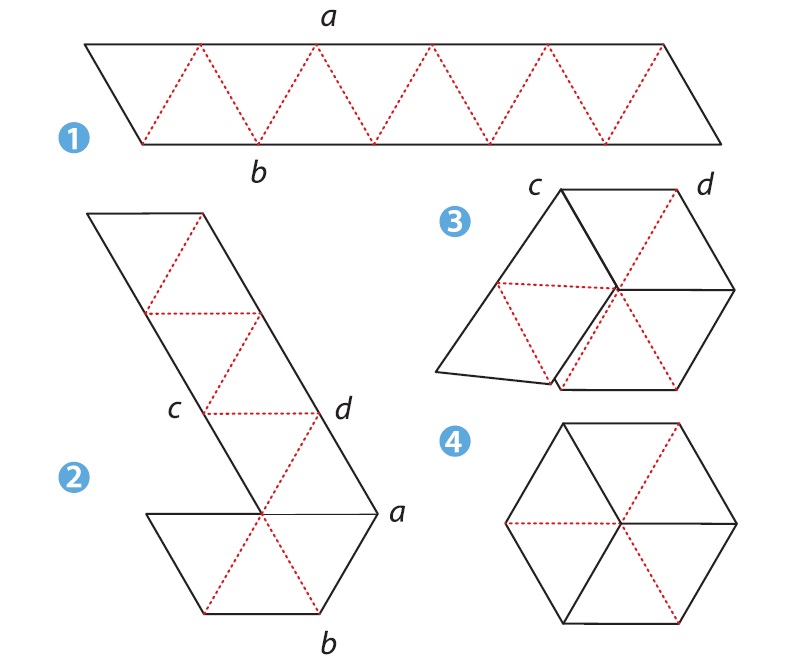
Рис.3.

1.  Виды флексагонов, их свойства

Исследуя данную тему, я столкнулся с огромным количеством видов флексагонов с очень длинными и пугающими названиями. Но всё оказалось очень просто.

Поверхности флексагона могут состоять из треугольников, квадратов, пятиугольников и т.д. Флексагон заданной формы с заданным количеством плоскостей может быть изготовлен из разных развёрток. При этом даже одна и та же развёртка может допускать разные варианты сворачивания. Общепринятой системы наименований для флексагонов нет.

Название флексагона содержит впереди числительное, показывающее, сколько плоскостей имеет этот флексагон, на втором месте — числительное, определяющее форму флексагона, и в заключение — известное уже слово, обозначающее, что всё это гнётся и складывается.

Вот несколько примеров приставок, образуемых из корней греческих числительных, применяемых для обозначений: 1– моно-, 2 – ди- или би-, 3 – три-, 4 – тетра-, 5 – пента-, 6 – гекса-, 7 – гепта-, 8 – окта- и т. д.

Унагексафлексагон - треугольный лист Мёбиуса. Полоску из трех треугольников разглаживают , и подвернув один конец соединяют с другим. Имеет одну поверхность. Не сгибается.

Рис.4.

Дуогексафлексагон- представляет собой просто шестиугольник, вырезанный из бумаги. У него две стороны, но он не складывается

Рис.5.

Тригексафлексагон- складывают из полоски бумаги, предварительно размеченной на 10 равносторонних треугольников; шестиугольный лист Мёбиуса. Имеет три поверхности. Может сгибаться.

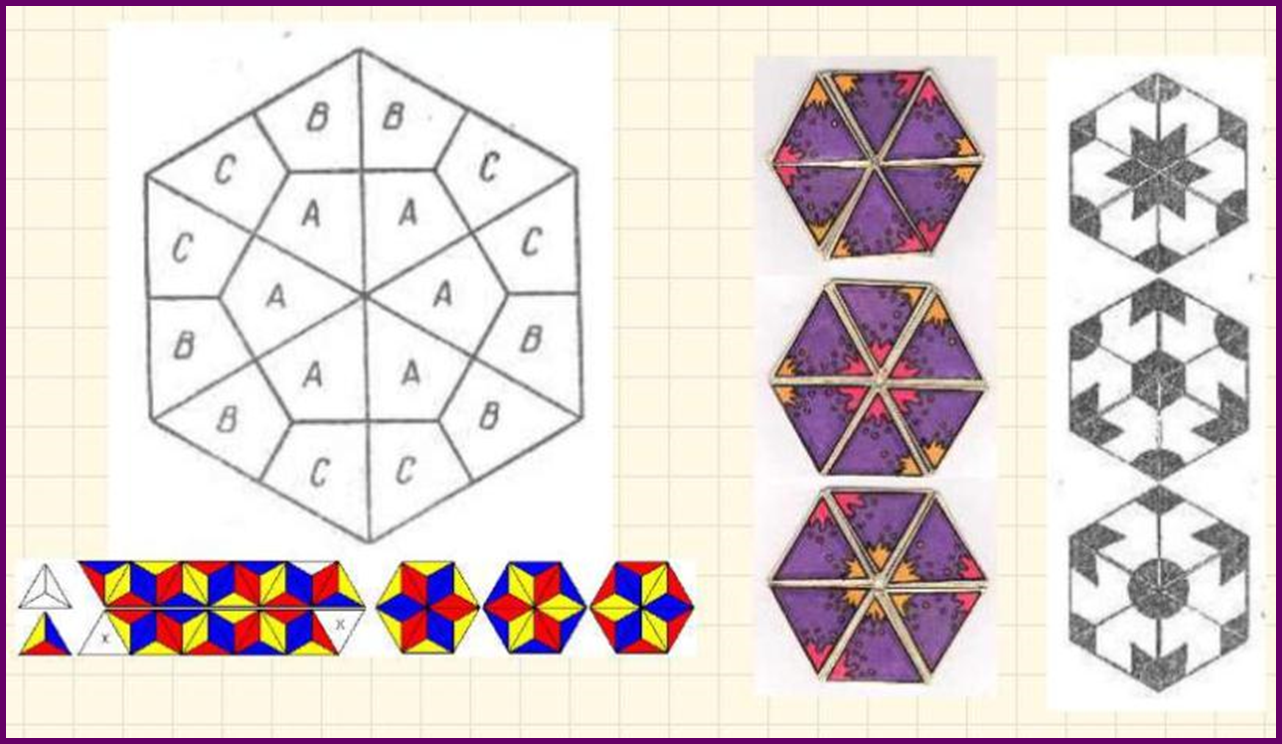
Рис.6.

Тетрагексафлексагон- Простейший тетрагексафлексагон имеет три поверхности и поэтому называется тритетрафлексагоном. Его легко сложить из полоски бумаги, изображенной на рисунке.

Тетрагексафлексагон- также существует по крайней мере шесть типов

четырехсторонних тетрафлексагонов, известных под названием тетратетрафлексагоны. Для изготовления их понадобится прямоугольный листок бумаги, разграфленный на 12 квадратов. Нумерация квадратов на обеих сторонах листа показана на рисунке. Пунктиром обозначены линии разрезов.

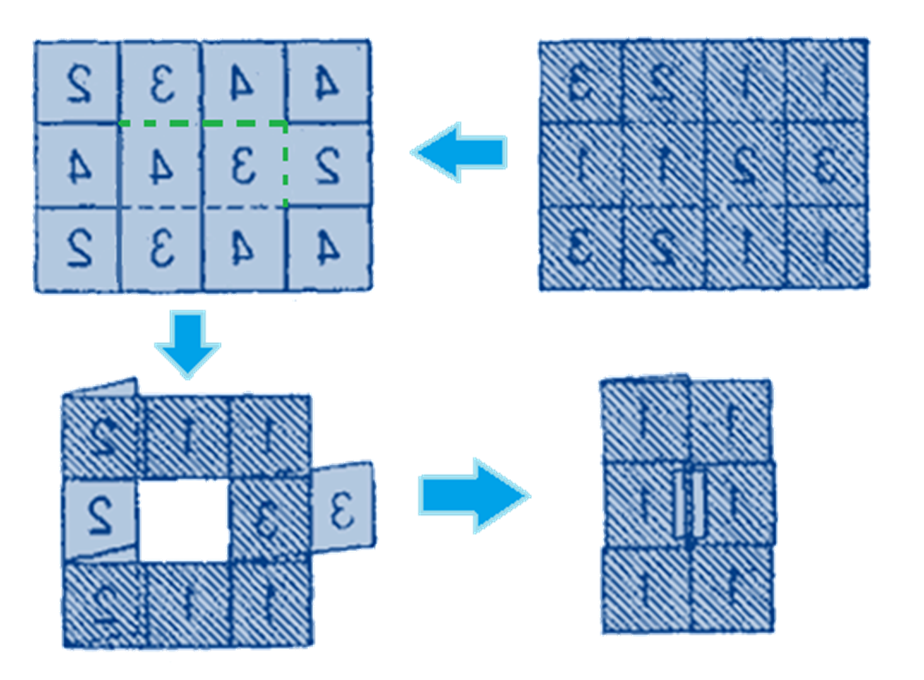
Рис.7.

Гептагексафлексагон - имеет семь поверхностей. Его складывают тремя способами из полосок бумаги, изображенных на рисунке.

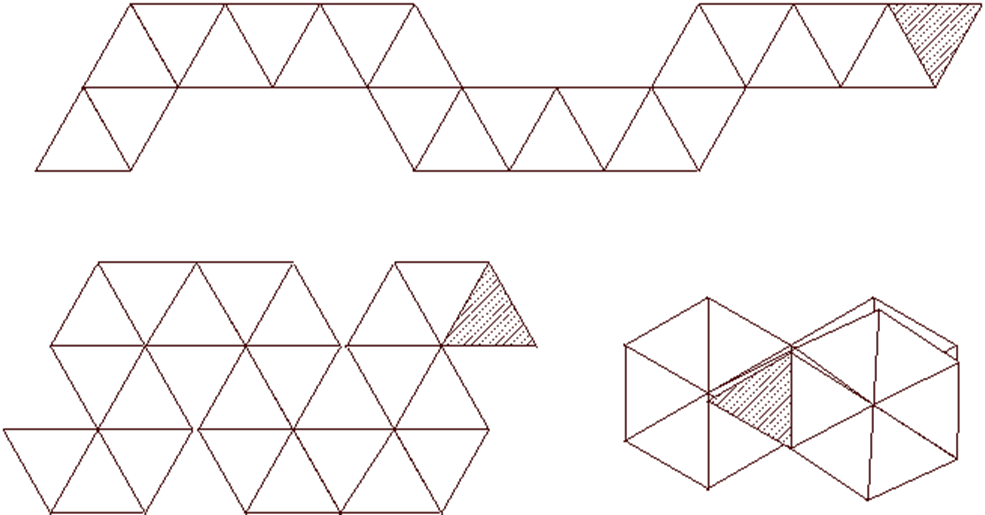
Рис.8.

Пентагексафлексаго- имеет пять поверхностей. Единственную разновидность этого флексагона складывают из полоски, показанной на рисунке.

Рис.9.

Гексагексафлексагон- складывают из полоски бумаги, разделенной на 19 равносторонних треугольников. Перегибая гексагексафлексагон, можно увидеть все шесть его разворотов

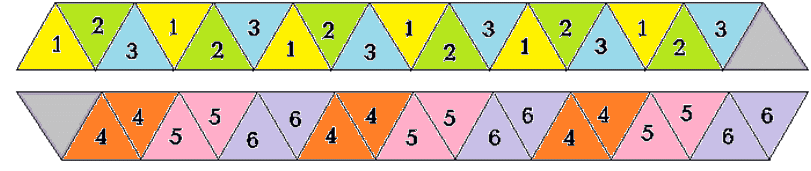
Рис.10

1. Методы складывания флексагонов

Возвращаясь к теме флексагонов, стоит упомянуть методы складывания, которые позволяют «обойти» все доступные поверхности пошагово. Было разработано несколько методов:

v-flex. Используется для гексафлексагонов, от четырех поверхностей; tuckflex. Еще одно название – «лодка-гексаэрд», можно выполнить на гексафлексагонах с количеством плоскостей от четырех и больше; pinchflex. Используется для гексафлексагонов с количеством плоскостей от трех и больше. Последний метод больше известен под названием обход Таккермана. Он считается одним из самых простых вариантов, рассмотреть все доступные поверхности гексафлексагона. Согласно инструкции, необходимо взять флексагон за один уголок и раскрывая его до того момента, пока это возможно. Далее его поворачивают на шестьдесят градусов по ходу часовой стрелки, берут за соседний уголок и снова поэтапно раскрывают до конца: https://vishivashka.ru/bez-rubriki/fleksagon.php

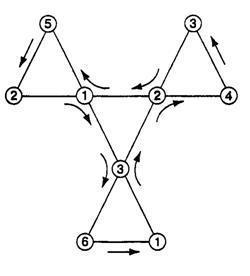
Рис. 11.

При использовании обхода, грани раскрываются в определенном порядке: 1, 2, 5, 1, 2, 3, 4, 2, 3, 1, 6, 3 (или в обратном направлении).

Этот порядок называется путь Таккермана.

Глава II. Флексагоны, как средство математического моделирования

Флексагоны и флексоры применяются как средство математического развития дошкольников и школьников младших классов.

  Флексагоны как средство математического моделирования имеют следующие отличительные черты:

 1)    Экономичность: для изготовления флексагонов нужны бумага, клей, ножницы и эталоны форм.

 2)    Доступность: при минимальной помощи взрослого ребенок не только находит скрытые поверхности флексагона, но и моделирует флексагоны по готовой развертке.

3)      Развитие: флексагоны способствуют развитию мелкой моторики, пространственного воображения, памяти, внимания, терпения; при специально продуманной раскраске активизируют формирование различных представлений по всем разделам математики для школьников и дошкольников и многое другое.

2.1. Мастер – класс по складыванию тригексафлексагона

Сложить свой первый из бумаги тригексафлексагон совсем не сложно, если следовать определенной схеме сборки. Делать это лучше всего опираться на мастер-класс для начинающих. См. Приложение 1.

Советы по изготовлению флексагонов

Прежде чем приступать к изготовлению флексагона, полезно несколько раз перегнуть в обе стороны его развертку по всем линиям сгиба. Это намного облегчает последующие манипуляции с флексагонами. Для более долговечных моделей, можно вырезать квадраты из картона или металла и соединить их липкой лентой или же наклеить на длинную полоску ткани.

Между квадратами остаются небольшие зазоры, что позволяет легко сгибать флексагоны.

2.2. Применение флексагонов

Флексагоны и флексоры применяются как средство математического развития дошкольников и школьников младших классов. Дети активно овладевают построением и использованием различных предметных, графических и мысленных моделей.

Флексор можно использовать в качестве фоторамки. На все треугольники одной поверхности приклеиваются фотографии (например, учеников класса). Этой фоторамке не требуется специальная подставка.

Необычно применение флексагона и в качестве шпаргалки. Написав на его сторонах формулы или правила, можно вывернуть флексагон обычными раскрашенными сторонами наружу.

Флексагоны и флексоры можно подарить друзьям в качестве сувенира или во время проведения праздника научить их делать эти геометрические игрушки.

Флексоры и простейшие флексагоны, раскрашенные в разные цвета или сделанные из фольги, можно использовать в качестве ёлочных украшений или для обычного оформления праздника.

Тетратетрафлексагон можно часто встретить в роли головоломки или рекламного буклета. Это связано с его особым свойством: одну из поверхностей отыскать гораздо сложнее, чем три других.

Широко применяется флексагон и при создании поздравительных открыток – трансформеров.

Применение флексагонов в жизни. См. Приложение 2

Заключение

Закончена работа над исследовательским проектом. Пройден трудный, но интересный путь:

• я познакомился с понятиями «флексагон»;

• изучил вопрос о происхождении флексагонов;

• нашел информацию и подробно изучил инструкции по конструированию отдельных видов флексагонов;

• изготовил модель флексагона;

• выявил области практического применения флексагонов в жизни человека.

Оглядываясь назад, можно с уверенностью сказать, что намеченные задачи выполнены, цель – изучение мира флексагонов – достигнута.

Моя работа предназначена тем, кто любит необычную и занимательную математику. Также работа может быть использована на уроках математики: при изучении свойств треугольников, шестиугольников, тетраэдров или на занятиях математического кружка.

В мире существует много неоткрытых загадочных вещей, которым ещё предстоит удивить нас своими замечательными свойствами.

Список информационных источников

1. Афонькин С. Игры и фокусы с бумагой / С. Афонькин, Е. Афонькина. — М.: Рольф, АКИМ, 1999. — С. 12–67.

2. сайт /tracks/4188813.html

http://www.osvetleni- daylight.cz/designova-stolni-lampa-flexagon-white-p-1466.html?zenid=f80a554ef57c674b587d29e31e443d52

https:/ Материал из Викиучебника — открытых книг для открытого мира

/school-science.ru/2/7/30072

Приложение 1

Изготовление тригексафлексагона

Подготовили шаблон

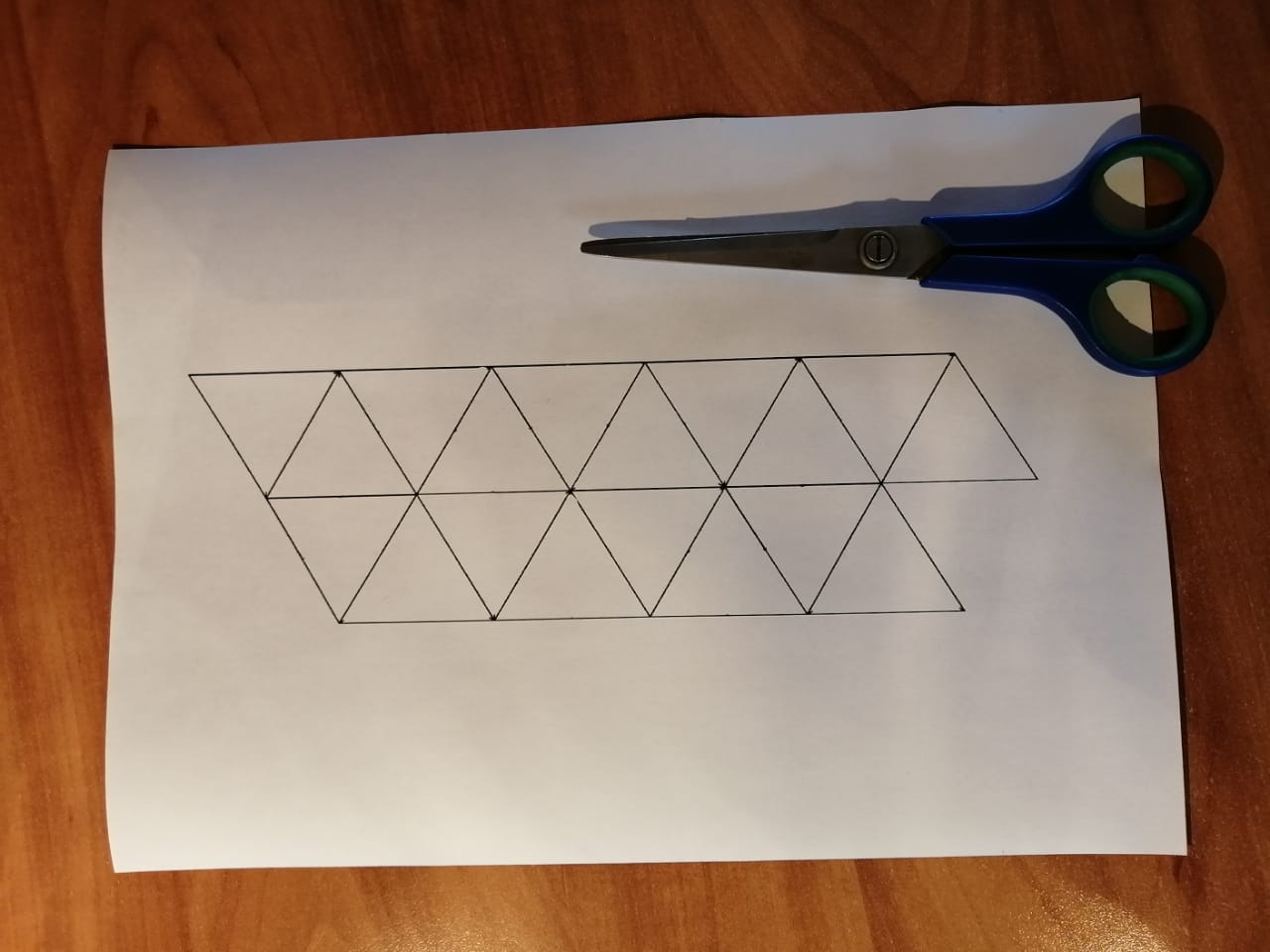
Вырезаем полосу и делим её на равносторонние треугольники

Сгибаем 1

Затем намечаем линии сгибов, чтобы бумажка легче сгибалась. И сворачиваем эту бумажную полоску.

Сгибаем 2

В итоге получится шестиугольник с одним торчащим треугольником

Этот хвостик-треугольника смазываем клеем и приклеиваем.

Получился тот самый первый флексагон, с которого всё и начиналось когда-то. Он называется тригексафлексагоном

Приложение 2

Применение флексагонов в жизни:

‒шарнирное соединение двойного действия на дверной петле

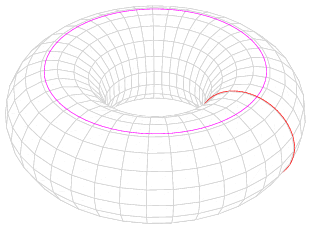
‒ Тор и лента Мебиуса ‒ связь флексагонов и математики

 ‒ лампа в стиле флексагона

Но большее применение, я думаю, многогранник найдет в дизайнерском деле: цикл перегибаний последовательно позволяет фигуре быть и диваном, и стулом, и креслом и, если убрать одну сторону куба,‒ полкой для вещей или комодом.

22