Муниципальное автономное общеобразовательное учреждение "Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина"
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
Диофантовы уравнения, типы и способы решения
Выполнила:
учащаяся 10 класса «А»
Лаврентьева Елизавета Андреевна
Подпись
Научный руководитель:
Сухненко Ирина Александровна,
учитель математики
Тамбов, 2022
Оглавление Введение 3
Цель и задачи 3
ОСНОВНАЯ ЧАСТЬ 5
Глава 1. Диофант и история диофантовых уравнений 5
Глава 2. О диофантовых уравнениях 7
Глава 2.1. Определение. Диофантовый анализ 7
Глава 2.2. Диофантовы уравнения первого порядка с двумя неизвестными 9
Глава 2.3. Диофантовы уравнения второго порядка с двумя неизвестными 13
Глава 2.4. Другие уравнения в целых числах 17
Глава 2.5. Неравенства в целых числах. Графические иллюстрации 18
ГЛАВА 3. Создание продукта 20
Заключение 21
Список литературы 22
Приложение 1 23
Приложение 2 24
ПРИЛОЖЕНИЕ 3 25
ПРИЛОЖЕНИЕ 4 27
Введение
В последние годы значительно возрос интерес к задачам, при решении которых используются свойства целых чисел. Это определено, в первую очередь, тем, что такие задачи часто встречаются на вступительных экзаменах в высшие учебные заведения и на олимпиадах по математике.
Диофантовы уравнения (задачи на целые числа) всегда считались одними из наиболее сложных задач, предлагаемых учащимся старших классов. Это объясняется отсутствием единого метода их решения.
Гипотеза: умение решать диофантовы уравнения позволяет оптимизировать многие процессы, найти остроумные и сравнительно простые решения «неразрешимых» задач, а в практической деятельности значительно сэкономит затраты средств и времени.
Объект исследования - диофантовы уравнения.
Предмет исследования - методы решения уравнений в целых числах.
Уравнения в математике занимают важное место. Большее количество задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений.
Актуальность данной темы обусловлена тем, что умение решать уравнения в целых числах окажется полезным при решении задач, выходящих за рамки школьной программы, олимпиадных заданий, а также задач с практическим содержанием в реальной жизни.
Цель работы: изучение диофантовых уравнений, их типов и способов решения.
В работе поставлены задачи:
Научиться быстро и грамотно находить информацию в интернете и научной литературе по данной теме, развить навыки проектной деятельности.
Изучить биографию Диофанта и ознакомиться с понятием «диофантовы уравнения».
Научиться решать уравнения в целых числах разных уровней сложности.
Разработать небольшое пособие, в котором изложена основная теория по диофантовым уравнениям, рассмотрены примеры.
Создать интерактивную работу, помогающую определить степень усвоения темы.
ОСНОВНАЯ ЧАСТЬ
Глава 1. Диофант и история диофантовых уравнений «Достопочтеннейший Дионисий, зная, что ты ревностно хочешь научиться решению задач, касающихся чисел, я попытался изложить природу их и могущество, начиная с тех оснований, на которых покоится эта наука.
Может быть, этот предмет покажется тебе затруднительным, поскольку ты еще с ним незнаком, а начинающие не склонны надеяться на успех. Но он станет тебе удобопонятным благодаря твоему усердию и моим пояснениям, ибо страстная любовь к науке помогает быстро воспринять учение»
Таким посвящением открывается «Арифметика» Диофанта Александрийского.
Диофант представляет одну из занимательных загадок в истории математики. Мы не знаем, кем был Диофант, точные года его жизни; полагают, что он жил в III в. н. э. На могиле Диофанта есть стихотворение - задача, решая которую нетрудно подсчитать, сколько лет прожил великий математик.
«Прах Диофанта гробница покоит; дивись ей - и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком,
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей».
Решение задачи сводится к решению уравнения первой степени с одним неизвестным.
Пусть x - количество лет, прожитых Диофантом, тогда 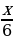 лет - он прожил ребенком, а
лет - он прожил ребенком, а 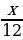 лет - он прожил до появления пуха на его подбородке,
лет - он прожил до появления пуха на его подбородке, 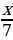 лет - Диофант провел в бездетном браке, спустя 5 лет у него родился сын, который прожил
лет - Диофант провел в бездетном браке, спустя 5 лет у него родился сын, который прожил 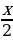 лет. Отец пережил сына на 4 года.
лет. Отец пережил сына на 4 года.
Составим и решим уравнение:
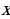 =
= 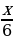 +
+ 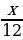 +
+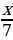 + 5 +
+ 5 +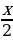 +4,
+4,
откуда 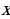 = 84.
= 84.
Эта головоломка служит примером тех задач, которые решал Диофант. Он специализировался на решении задач в целых числах. Такие задачи в настоящее время известны под названием диофантовых.
Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». «Арифметика» Диофанта — это сборник 189 задач с решениями, сводящимися к определенным уравнениям первой и второй степеней и неопределенным. Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.
Глава 2. О диофантовых уравнениях Глава 2.1. Определение. Диофантовый анализ Диофантовыми уравнениями называют алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух (если не ограничиваться только целыми числами).
Диофантовыми уравнениями называются уравнения вида
P(x1, x2, ..., xn) = 0,
где P(x1, ..., xn) - многочлен с целыми коэффициентами.
Проблема решения уравнений в целых числах решена до конца только для уравнений первой степени и для уравнений второй степени с двумя неизвестными. Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, не известно, имеет ли уравнение
x3 + y3 + z3 = 30
хотя бы одно целочисленное решение. Более того, доказано, что в принципе не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения.
Уравнение x2 + y2 = z2, связывающее стороны x, y, z прямоугольного треугольника, всегда вызывало большой интерес. Натуральные числа x, y и z, являющиеся решениями этого уравнения, называются «пифагоровыми тройками».
Неопределенное уравнение Ферма (уравнение Пелля). К работам Диофанта имеют непосредственное отношение и математические исследования французского математика Пьера Ферма. Считается, что именно с работ Ферма началась новая волна в развитии теории чисел.
x2 - ay2 = 1, где a — целое положительное число, не являющееся полным квадратом.
В 1630 г. французский математик Пьер Ферма сформулировал гипотезу, которую называют великой теоремой Ферма: «Уравнение xn + yn = zn для натурального n ≥ 3 не имеет решений в натуральных числах».
Глава 2.2. Диофантовы уравнения первого порядка с двумя неизвестными Диофантовым уравнением первого порядка с двумя неизвестными x, y будем называть уравнение вида ax + by = c, где a, b, c, x, y 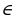 Z. Будем считать, что a и b – взаимно простые числа. Если это не так, то всегда можно сократить обе части уравнения на наибольший общий делитель (НОД) чисел a и b (если при этом в правой части получится нецелое число, то такое уравнение не будет иметь решений). Далее метод решения зависит от того, насколько большие модули чисел a и b. Если хотя бы один из коэффициентов (пусть a) невелик по модулю, перепишем уравнение в виде
Z. Будем считать, что a и b – взаимно простые числа. Если это не так, то всегда можно сократить обе части уравнения на наибольший общий делитель (НОД) чисел a и b (если при этом в правой части получится нецелое число, то такое уравнение не будет иметь решений). Далее метод решения зависит от того, насколько большие модули чисел a и b. Если хотя бы один из коэффициентов (пусть a) невелик по модулю, перепишем уравнение в виде
ax = c – by.
Левая часть полученного выражения делится нацело на a. Значит, должна делиться нацело на a и правая часть этого уравнения. Рассматривая всевозможные остатки l от деления y на a; l = 0, 1, …, a - 1, получим, что при одном значении l из указанного промежутка будет делиться на a и правая часть. Поскольку число a не велико по модулю, то и перебор вариантов будет тоже невелик.
Теоремы о числе целых решений диофантового уравнения первого порядка с двумя неизвестными.
Теорема 1. Если свободный член c диофантового уравнения ax + by = c не делится на НОД(a, b), то уравнение не имеет целых решений.
Теорема 2. Если коэффициенты a и b неопределенного уравнения ax + by = c являются взаимно простыми числами, то уравнение имеет по крайней мере одно целое решение.
Теорема 3. Если в уравнении ax + by = с, НОД(a, b) = 1, то все целые решения этого уравнения заключены в формулах:
x = x0 + b * t, y = y0 – a * t,
где (x0 ; y0 ) – некоторое решение уравнения ax + by = с, a t – произвольное целое число.
Посмотрим на практике, как работает метод подбора для решения уравнений в целых числах.
Пример 1. Решить уравнение 3х - 4у = 1 в целых числах.
Решение. Перепишем уравнение в виде 3х = 4у + 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая.
Если у = 3t; t 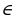 Z, то 4у + 1 = 12t + 1 не делится на 3.
Z, то 4у + 1 = 12t + 1 не делится на 3.
Если у = 3t + 1, то 4у + 1= 4(3t + 1) + 1 = 12t + 5 не делится на 3.
Если у = 3t + 2, то 4у + 1 = 4(3t + 2) +1 = 12t + 9 делится на 3, поэтому 3х = 12t + 9, т.е. x = 4t + 3.
Ответ: {(4t + 3, 3t + 2)}; t ∈ Z.
Метод рассмотрения остатков становится неэффективным, если числа 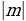 и
и 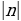 являются большими простыми числами. В этом случае применяется алгоритм, основанный на последовательном уменьшении по модулю коэффициентов при неизвестных (метод спуска или метод рассеивания).
являются большими простыми числами. В этом случае применяется алгоритм, основанный на последовательном уменьшении по модулю коэффициентов при неизвестных (метод спуска или метод рассеивания).
Алгоритм:
Выбор наибольшего по модулю коэффициента (пусть 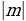
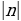 ).
).
Проведение процедуры уменьшения коэффициентов. Это делается с помощью деления с остатком. Пусть n = l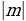 + q, где 0 q ≤
+ q, где 0 q ≤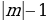 , тогда mx + ny = k
, тогда mx + ny = k  mx + (l
mx + (l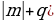 y = k
y = k  mx + l
mx + l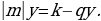
Левая часть последнего уравнения делится на m и правая часть: k – qy = mt, где t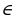 Z, t – новое неизвестное.
Z, t – новое неизвестное.
Повторение процедуры уменьшения коэффициентов. Новое уравнение отличается от старого только тем, что его коэффициенты по модулю меньше коэффициентов старого. За конечное число шагов добьемся того, что коэффициент при одном из новых неизвестных будет равен 1.
Возврат к исходным переменным.
Пример 2. Решить уравнение 79y – 23x = 1 в целых числах.
Решение. Проведем деление с остатком: 79 = 23*3 + 10 и перепишем исходное уравнение в виде 23x = 79y - 1 = (23*3 + 10)y – 1 = 69y + 10y - 1 23x - 69y = 10y - 1.
23x - 69y = 10y - 1.
Левая часть уравнения делится нацело на 23, поэтому должна делиться на 23 и правая часть: 10y – 1 = 23t или 10y = 23t + 1; t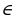 Z – новое неизвестное.
Z – новое неизвестное.
Полученное новое уравнение по типу точно такое же, как исходное. Однако коэффициенты при неизвестных в нем уменьшились по модулю. Повторим процедуру уменьшения коэффициентов еще раз: 10y = 23t + 1 = (10*2 + 3)t + 1 10y – 20t = 3t +1
10y – 20t = 3t +1 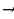 3t + 1 = 10u, u
3t + 1 = 10u, u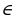 Z – новое неизвестное. Проведем процедуру уменьшения коэффициентов в последний раз: 3t + 1 = 10u = (3*3 + 1)u
Z – новое неизвестное. Проведем процедуру уменьшения коэффициентов в последний раз: 3t + 1 = 10u = (3*3 + 1)u 3t - 9u = u - 1
3t - 9u = u - 1 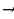 u - 1 = 3v, v
u - 1 = 3v, v 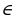 Z.
Z.
Осталось выразить x и y через v. Поскольку u = 3v + 1, то
3t = 10u – 1 = 10(3v + 1) - 1 = 30v + 9 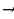 t = 10v + 3.
t = 10v + 3.
10y = 23t +1 = 23(10v + 3) + 1 = 230v + 70 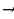 y = 23v + 7.
y = 23v + 7.
23x = 79y – 1 = 79(23v + 7) - 1=79*23v + 552 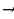 x = 79v + 24.
x = 79v + 24.
Ответ: {(79v + 24, 23v + 7)}; v ∈ Z.
Пример 3. Решить уравнение 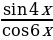 = 1.
= 1.
Решение. Преобразуем данное уравнение следующим образом:
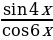 = 1
= 1 
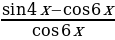 = 0
= 0 
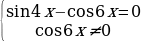

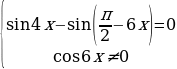

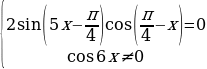

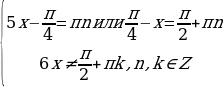

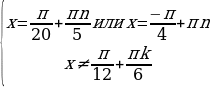
Решим два уравнения в целых числах. Рассмотрим сначала первое уравнение:
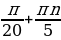 =
= 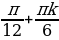
 5k = 6n – 1.
5k = 6n – 1.
Перебирая все возможные остатки при делении n на 5, находим, что решением последнего уравнения являются n = 5l + 1; l 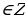 . Значит, решением задачи будут служить x =
. Значит, решением задачи будут служить x = 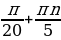 , где
, где
n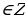 , n
, n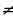 5l + 1; l
5l + 1; l 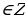 . Теперь рассмотрим второе уравнение:
. Теперь рассмотрим второе уравнение:
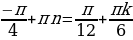
 6n = 2 + k.
6n = 2 + k.
Ясно, что любое целое n является решением этого уравнения. Таким образом, ни одно значение x из серии x = 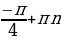 не удовлетворяют условию задачи.
не удовлетворяют условию задачи.
Ответ: 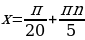 ; n
; n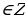 , n
, n 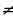 5l + 1; l
5l + 1; l 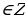 .
.
Глава 2.3. Диофантовы уравнения второго порядка с двумя неизвестными Диофантовым уравнением второго порядка с двумя неизвестными x, y будем называть уравнение вида
Ax2 + Bxy + Cy2 + Dx + Ey = F,
где A, B, C, D, E, F, x, y 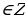 и хотя бы одно из чисел A, B, C отлично от нуля.
и хотя бы одно из чисел A, B, C отлично от нуля.
Рассмотрим основные методы решения данных уравнений.
Разложение на множители. Этот метод состоит в том, что левая часть данного уравнения каким-либо образом раскладывается на множители (чаще всего путем нахождения дискриминанта), и задача сводится к перебору конечного числа вариантов.
Пример 1. Найти все пары целых чисел (x, y), каждая из которых удовлетворяет уравнению 2x2 + 5 = 3y2 + 5xy.
Решение. Преобразуем данное уравнение следующим образом:
2x2 + 5 = 3y2 + 5xy  3y2 + 5xy - 2x2 = 5
3y2 + 5xy - 2x2 = 5  (3y - x)(y + 2x) = 5
(3y - x)(y + 2x) = 5 
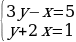 или
или 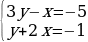 или
или 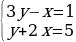
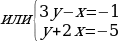 .
.
Первые две системы не имеют решений в целых числах, третья и четвертая имеют решением пары (x, y) = (2, 1) и (x, y) = (-2, -1) соответственно.
Ответ: {(2,1); (-2, -1)}.
Если в уравнении отсутствует член, содержащий 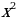 или
или 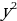 , т.е. A либо С равно нулю, но при этом В
, т.е. A либо С равно нулю, но при этом В 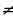 0, то такое уравнение решается методом выделения целой части. Пусть, например, A = 0. Выразим x через у:
0, то такое уравнение решается методом выделения целой части. Пусть, например, A = 0. Выразим x через у:
Bxy + Cy2 + Dx + Ey = F  x(By + D) = F – Ey - Cy2, откуда x =
x(By + D) = F – Ey - Cy2, откуда x = 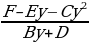 . Далее делим многочлен F – Ey - Cy2 на многочлен By + D с остатком, т.е. представляем данную дробь в виде
. Далее делим многочлен F – Ey - Cy2 на многочлен By + D с остатком, т.е. представляем данную дробь в виде
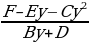 = Py + Q +
= Py + Q + 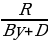 ,
,
где P, Q, R – рациональные числа. Подобрав, при необходимости, целое число T и домножив на него обе части уравнения
x = Py + Q + 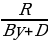 ,
,
получим уравнение
Tx = P’y + Q’ + 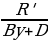 ,
,
где P’, Q’ и R’ уже являются целыми числами. Дальнейшее решение сводится к перебору всех делителей числа R’ (если R’ = 0, то уравнение становится линейным).
Пример 2. Решить в целых числах уравнение 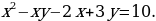
Решение. Выразим в данном уравнении y через x:
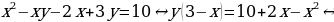 y =
y = 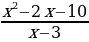 = x + 1 -
= x + 1 - 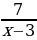 .
.
Из полученного равенства видно, что дробь 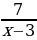 должна быть целым числом. Это возможно, когда x – 3 принимает значения
должна быть целым числом. Это возможно, когда x – 3 принимает значения 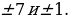 Разбирая четыре случая, находим все пары (x, y), удовлетворяющие данному уравнению: (x, y) = {(10, 10); (-4, -2); (4, -2); (2, 10)}.
Разбирая четыре случая, находим все пары (x, y), удовлетворяющие данному уравнению: (x, y) = {(10, 10); (-4, -2); (4, -2); (2, 10)}.
Ответ: {(10, 10); (-4, -2); (4, -2); (2, 10)}.
Если диофантово уравнение второго порядка каким-либо образом (например, выделением полных квадратов) приводится к виду Ax2 + Cy2 = F, где A, C и F – целые, отличные от нуля, числа, то метод решения зависит от знаков коэффициентов при переменных. Если А и С имеют один и тот же знак, то используются следующие оценки (пусть A, C, F 0):
Ax2 + Cy2 = F 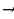 x2
x2 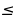
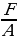

Далее задача сводится к перебору конечного числа вариантов. Если же А и С имеют разные знаки, то в общем виде решение уравнения достаточно сложно, но в некоторых случаях можно, например, перебором остатков доказать, что уравнение не имеет решений в целых числах.
Пример 3. Найти целочисленные решения уравнения 14x4 – 5y4 – 3x2y2 + 82y2 – 125x2 + 51 = 0.
Решение. Рассмотрим данное уравнение как квадратное относительно x2. Имеем: 14x4 – 5y4 – 3x2y2 + 82y2 – 125x2 + 51 = 0  14x4 – x2 (3y2 + 125) - 5y4 + 82y2 + 51 = 0.
14x4 – x2 (3y2 + 125) - 5y4 + 82y2 + 51 = 0.
Дискриминант этого уравнения равен D = (3y2 + 125)2 + 56(5y4 - 82y2 – 51) = 289y4 - 3842y2 + 12769 = (17y2 - 113)2.
Корни уравнения равны
x2 = 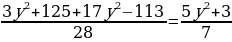
или
x2 = 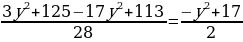 .
.
Таким образом, левая часть исходного уравнения раскладывается на множители следующим образом:
(7x2 – 5y2 – 3)(2x2 + y2 – 17) = 0,
и задача сводится к решению двух уравнений в целых числах.
Докажем сначала, что уравнение 7x2 = 5y2 + 3 не имеет целочисленных решений. Для этого посмотрим, какие остатки могут давать при делении на 3 левая и правая части этого уравнения. Так как любой полный квадрат дает при делении на 3 остаток 0 или остаток 1, число 7x2 также дает при делении на 3 остатки 0 и 1. Остатки от деления на 3 числа 5y2 + 3 могут быть равны 0 или 2. Таким образом, равенство может иметь место только в том случае, когда x и y кратны 3. Но в этом случае числа x2 и 5y2 делятся без остатка на 9, поэтому равенство также не может иметь место (поскольку 3 не делится на 9).
Рассмотрим теперь уравнение 2x2 + y2 – 17. Из оценки x2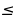 8,5 сразу следует, что x по модулю не превосходит 2. Перебирая все возможные варианты, находим, что решением задачи будут служить пары чисел (x, y) = {(2, 3); (-2, 3); (-2, -3); (2, -3)}.
8,5 сразу следует, что x по модулю не превосходит 2. Перебирая все возможные варианты, находим, что решением задачи будут служить пары чисел (x, y) = {(2, 3); (-2, 3); (-2, -3); (2, -3)}.
Ответ: {(2, 3); (-2, 3); (-2, -3); (2, -3)}.
Наконец, рассмотрим уравнение вида Ax2 + Dx + Ey = F, где A, D, E, F – целые числа и А, и Е отличны от нуля. Это уравнение решается перебором остатков при делении на Е числа F – Dx - Ax2. Но в отличие уравнений первого порядка разрешимость данного уравнения может быть и при нескольких значениях остатка q. Кроме того, может оказаться, что такое уравнение и вовсе не имеет решений.
Пример 4. Решить в целых числах уравнение 3x2 + 2x + 3y = 2.
Решение. Перепишем исходное уравнение в виде 3y = 2 – 2x - 3x2.
Левая часть полученного уравнения делится на 3, значит, должна делиться на 3 и его правая часть. Рассмотрим три случая.
Если x = 3k; k 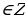 , то 2 – 2x - 3x2 = 2 – 6k – 27k2 не делится на 3.
, то 2 – 2x - 3x2 = 2 – 6k – 27k2 не делится на 3.
Если x = 3k + 1, то 2 – 2x - 3x2 = 2 – 2(3k + 1) – 3(3k + 1)2 = - 27k2 - 24k – 3 делится на 3.
Если x = 3k + 2, то 2 – 2x - 3x2 = 2 – 2(3k + 2) – 3(3k + 2)2 = - 27k2 - 42k – 14 не делится на 3.
Итак, x = 3k + 1, откуда y = - 9k2 - 8k – 1, где k 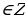 .
.
Ответ: {(3k + 1, - 9k2 - 8k – 1)}; k 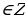 .
.
Рассмотрим на примере метод выделения полного квадрата.
Пример 5. Найти целочисленные решения 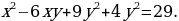
Решение.
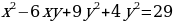
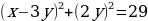
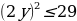
Значит, y = 0; 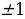 ;
; 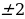 .
.
Перебрав все варианты значений y, и найдя соответствующие значения x, запишем ответ.
Ответ: {(2, -1); (-2; 1); (8; 1); (-8; -1)}.
Глава 2.4. Другие уравнения в целых числах Все описанные в предыдущем разделе методы применимы для решения не только диофантовых уравнений второго порядка с двумя неизвестными, но и других уравнений в целых числах. К таким уравнениям относятся уравнения второго порядка с тремя и более переменными, уравнения более высокого, чем второго, порядка. Выбор нужного метода при решении подобного уравнения порой является определяющим условием для успешного решения задачи. Рассмотрим несколько примеров.
Пример 1. Решить в целых числах уравнение x2 + 5y2 + 34z2 + 2xy – 10xz – 22yz = 0.
Решение. Преобразуем данное уравнение следующим образом:
x2 + 5y2 + 34z2 + 2xy – 10xz – 22yz = 0 
(x2 + 2x(y - 5z) + y2 – 10yz + 25z2) + 4y2 - 12yz + 9z2 = 0 
(x + y – 5z)2 + (2y – 3z)2 = 0 
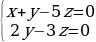

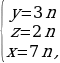 n
n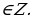
Ответ: x = 7n, y = 3n, z = 2n; n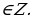
Пример 2. Найти все пары целых чисел (x, y), каждая из которых удовлетворяет уравнению (x2 + y2)(x + y – 3) = 2xy.
Решение. Ясно, что пара (0, 0) является решением данного уравнения. Предположим теперь, что хотя бы одно из чисел x и y отлично от нуля. Имеем
(x2 + y2)(x + y – 3) = 2xy  x + y – 3 =
x + y – 3 = 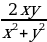
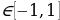 при всех значениях x и y. Так как x + y – 3 – целое число, то возможны три варианта.
при всех значениях x и y. Так как x + y – 3 – целое число, то возможны три варианта.
Если x + y – 3 = - 1, то x = - y, нет решений.
Если x + y – 3 = 0, то либо x = 0, y = 3, либо x = 3, y = 0.
Если x + y – 3 = 1, то x = y, следовательно, x = 2 и y = 2.
Ответ: {(2, 2); (3, 0); (0, 3); (0, 0)}.
Глава 2.5. Неравенства в целых числах. Графические иллюстрации Часто при решении уравнений, неравенств, систем, а также текстовых задач, связанных с целыми числами, удобно пользоваться графической иллюстрацией. Иногда удается достаточно несложно изобразить множество решений на координатной плоскости, и возникает необходимость выделить из этого множества точки с целочисленными координатами. Рассмотрим примеры.
Пример 1. Найти все целочисленные решения системы
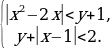
Решение.
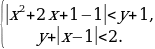
Пусть t = x – 1, тогда данная система примет следующий вид:
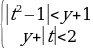

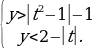
На координатной плоскости Oty полученная система определяет множество точек, изображенное в приложении 1.
Из рисунка видно, что в полученном множестве содержатся только три точки с целочисленными координатами – это (t, y) = {(-1, 0); (1, 0); (1, 1)}. Таким образом, ответом к задаче будут служить пары чисел (x, y) = {(0, 0); (2, 0); (1, 1)}.
Ответ: {(0, 0); (2, 0); (1, 1)}.
Пример 2. Найти все пары целых чисел x, y, удовлетворяющих системе
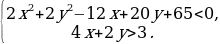
Решение. Преобразуем данную систему следующим образом:
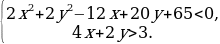

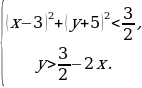
На координатной плоскости Oxy полученная система определяет множество точек, изображенное в приложении 2.
Из рисунка видно, что этому множеству принадлежат только две точки с целочисленными координатами – это точки (3, -4) и (4, -5).
Ответ: {(3, -4); (4, -5)}.
ГЛАВА 3. Создание продукта Я разработала небольшое пособие, в котором изложена основная теория по данной теме, рассмотрены примеры. Картинки смотреть в приложении 3.
С помощью программы iSpring Presenter я создала интерактивную работу, с помощью которой каждый сможет определить степень усвоения темы «Диофантовы уравнения». Картинки прикреплены в приложении 4.
Заключение
Решение уравнений в целых числах – один из самых красивых и интересных разделов математики, именно поэтому изучение данной темы показалось мне по-настоящему полезным и не скучным.
Целью моей работы являлось изучение диофантовых уравнений, их типов и способов решения. Использовав материалы по данной теме, я выполнила все поставленные передо мной задачи:
Расширила свои математические навыки и получила представление о работе над исследовательским проектом.
Изучила биографию Диофанта и ознакомилась с понятием «диофантовы уравнения».
Научилась решать уравнения в целых числах разных уровней сложности.
Разработала небольшое пособие, в котором изложена основная теория по уравнениям в целых числах, рассмотрены примеры.
Создала интерактивную работу, помогающую определить степень усвоения темы.
Говоря о практическом использовании полученных результатов нельзя не вспомнить слова Алексея Николаевича Крылова: «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».
Надеюсь, что многих заинтересует данная тема и они захотят познакомиться с ней поближе.
Список литературы
Башмакова И. Г. Диофант и диофантовы уравнения – М.: Наука, 1972 / И. Г. Башмакова. - Арифметика и книга о многоугольных числах - М.: Наука, 1974.
Гельфонд А. О. Решения уравнений в целых числах - М.: Наука, 1952.
Пичугин Л. Ф. За страницами учебника алгебры - М., 1990.
Интернет-источники:
http://www.math.md/school/krujok/diofantr/diofantr.html
https://lib.brsu.by/sites/default/files/books/УМП%20Грин
https://4ege.ru/matematika/59230-diofantovy-uravneniya.html
https://refdb.ru/look/3948362.html
Приложение 1
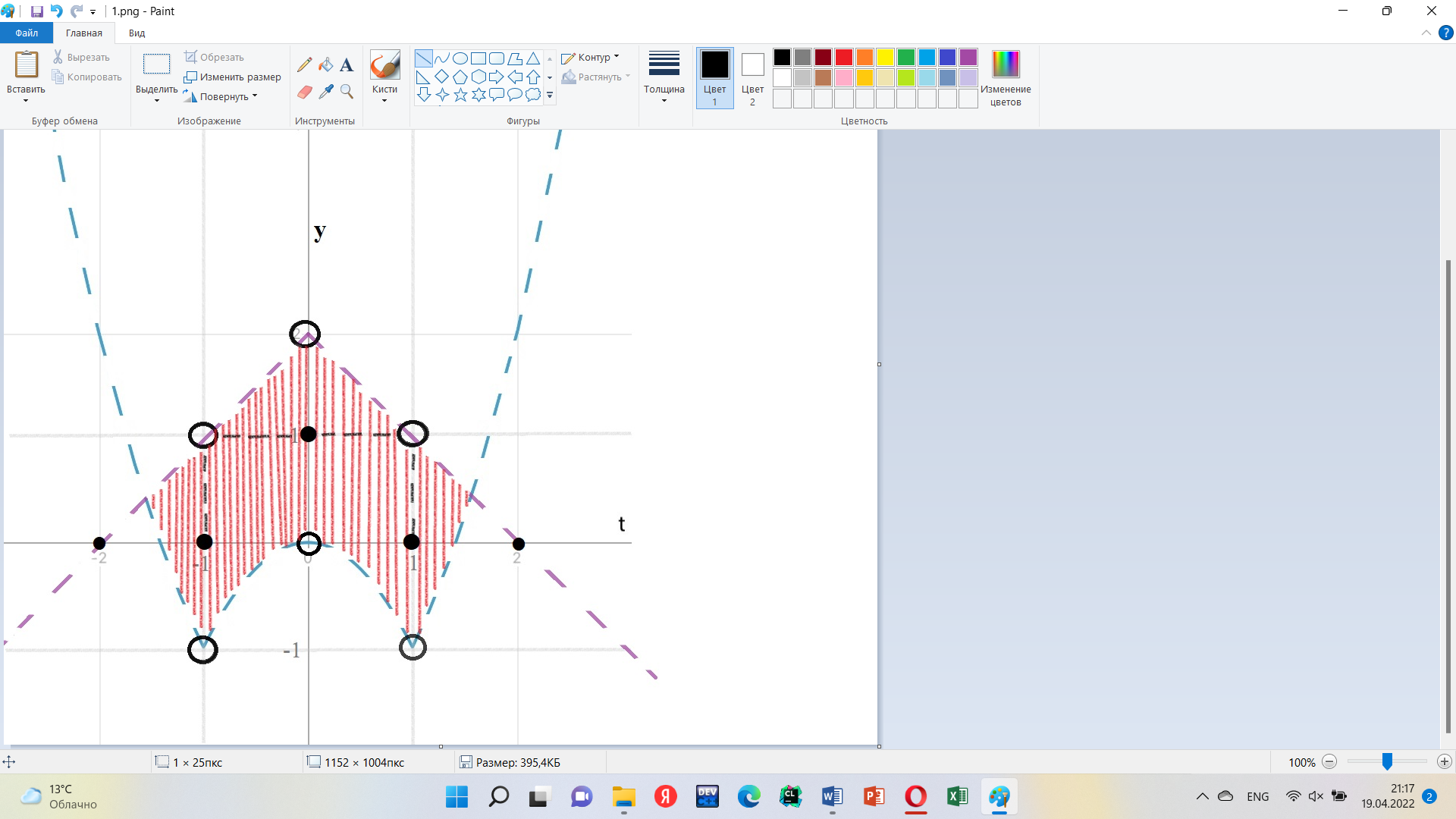
Рисунок 1. Графическая иллюстрация решения системы уравнений
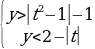 .
.
Приложение 2
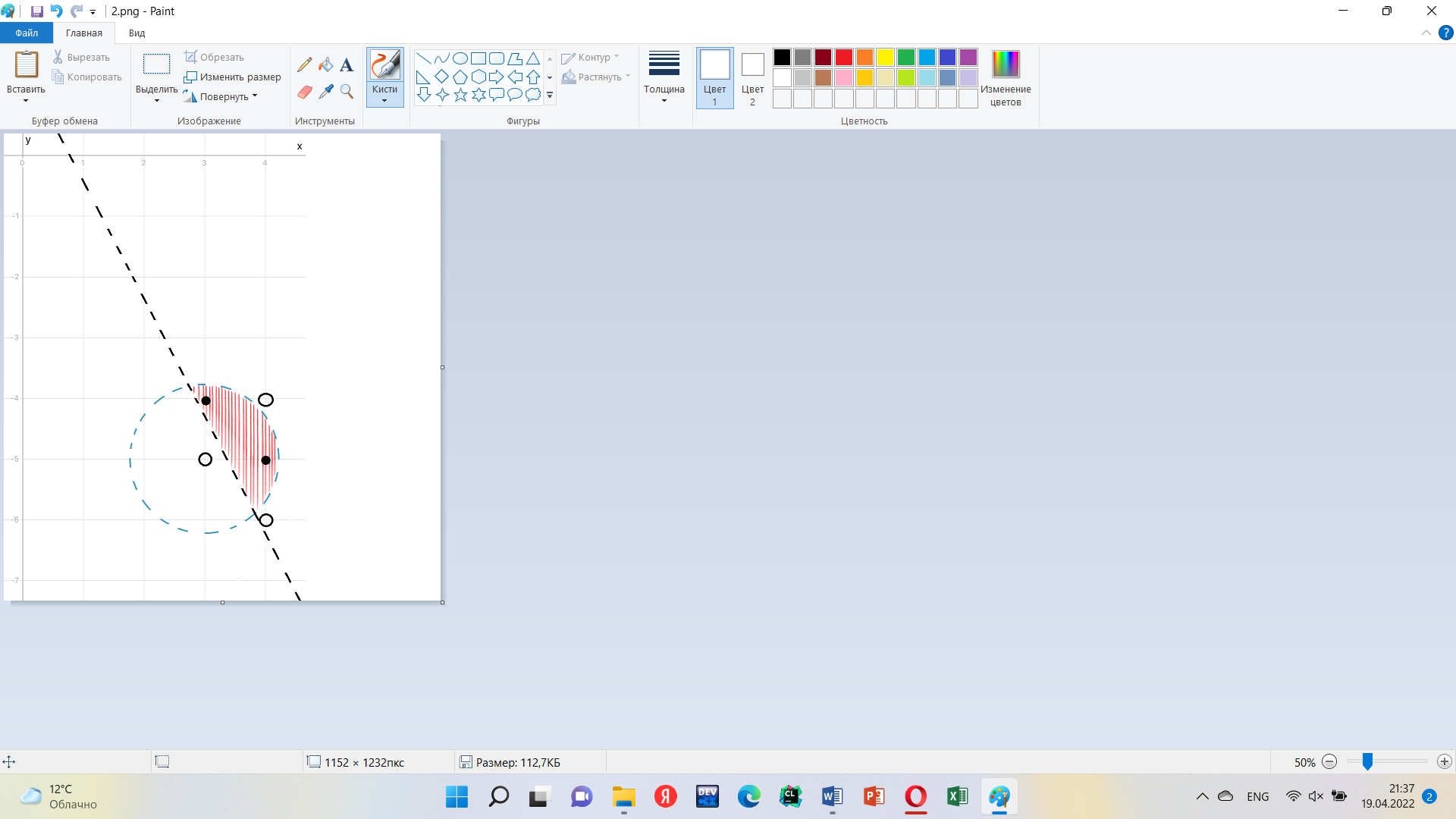
Рисунок 2. Графическая иллюстрация решения системы уравнений 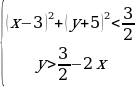 .
.
ПРИЛОЖЕНИЕ 3
Рисунок 3. Пособие.
Рисунок 4. Пособие.
ПРИЛОЖЕНИЕ 4
Рисунок 5. Интерактивная работа.
Рисунок 6. Интерактивная работа.







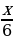 лет - он прожил ребенком, а
лет - он прожил ребенком, а 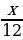 лет - он прожил до появления пуха на его подбородке,
лет - он прожил до появления пуха на его подбородке, 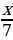 лет - Диофант провел в бездетном браке, спустя 5 лет у него родился сын, который прожил
лет - Диофант провел в бездетном браке, спустя 5 лет у него родился сын, который прожил 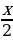 лет. Отец пережил сына на 4 года.
лет. Отец пережил сына на 4 года. 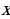 =
= 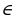 Z. Будем считать, что a и b – взаимно простые числа. Если это не так, то всегда можно сократить обе части уравнения на наибольший общий делитель (НОД) чисел a и b (если при этом в правой части получится нецелое число, то такое уравнение не будет иметь решений). Далее метод решения зависит от того, насколько большие модули чисел a и b. Если хотя бы один из коэффициентов (пусть a) невелик по модулю, перепишем уравнение в виде
Z. Будем считать, что a и b – взаимно простые числа. Если это не так, то всегда можно сократить обе части уравнения на наибольший общий делитель (НОД) чисел a и b (если при этом в правой части получится нецелое число, то такое уравнение не будет иметь решений). Далее метод решения зависит от того, насколько большие модули чисел a и b. Если хотя бы один из коэффициентов (пусть a) невелик по модулю, перепишем уравнение в виде 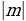 и
и 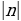 являются большими простыми числами. В этом случае применяется алгоритм, основанный на последовательном уменьшении по модулю коэффициентов при неизвестных (метод спуска или метод рассеивания).
являются большими простыми числами. В этом случае применяется алгоритм, основанный на последовательном уменьшении по модулю коэффициентов при неизвестных (метод спуска или метод рассеивания).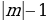 , тогда mx + ny = k
, тогда mx + ny = k  mx + (l
mx + (l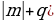 y = k
y = k 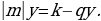
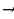 3t + 1 = 10u, u
3t + 1 = 10u, u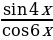 = 1.
= 1.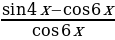 = 0
= 0 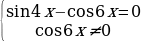
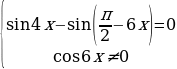
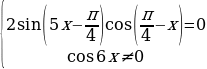
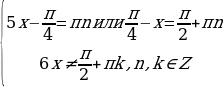
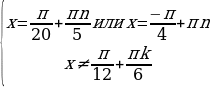
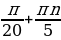 =
= 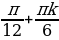
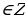 . Значит, решением задачи будут служить x =
. Значит, решением задачи будут служить x = 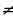 5l + 1; l
5l + 1; l 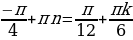
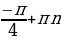 не удовлетворяют условию задачи.
не удовлетворяют условию задачи.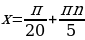 ; n
; n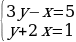 или
или 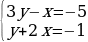 или
или 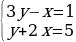
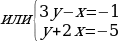 .
.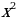 или
или 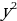 , т.е. A либо С равно нулю, но при этом В
, т.е. A либо С равно нулю, но при этом В 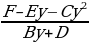 . Далее делим многочлен F – Ey - Cy2 на многочлен By + D с остатком, т.е. представляем данную дробь в виде
. Далее делим многочлен F – Ey - Cy2 на многочлен By + D с остатком, т.е. представляем данную дробь в виде 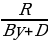 ,
, 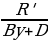 ,
, 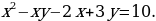
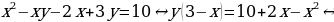 y =
y = 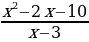 = x + 1 -
= x + 1 - 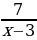 .
.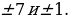 Разбирая четыре случая, находим все пары (x, y), удовлетворяющие данному уравнению: (x, y) = {(10, 10); (-4, -2); (4, -2); (2, 10)}.
Разбирая четыре случая, находим все пары (x, y), удовлетворяющие данному уравнению: (x, y) = {(10, 10); (-4, -2); (4, -2); (2, 10)}.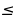
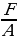
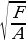
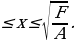
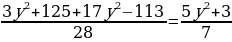
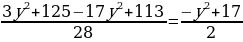 .
.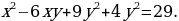
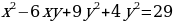
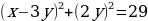
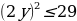
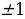 ;
; 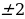 .
.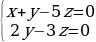
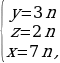 n
n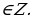
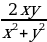
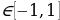 при всех значениях x и y. Так как x + y – 3 – целое число, то возможны три варианта.
при всех значениях x и y. Так как x + y – 3 – целое число, то возможны три варианта.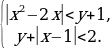
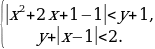
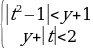
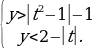
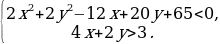
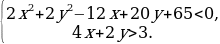
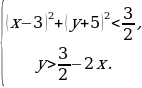

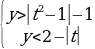 .
.
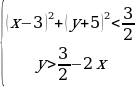 .
.






















