Информационный проект " Графы и их применение"

Автор работы : Красикова Диана Руководитель проекта: Хубулеева Галина Васильевна.

Учреждение: МОУ « СОШ Поселья»

Класс: 7 «а»

Номинация: Математика в практической деятельности

Тема: «Графы и их применение»

2020-2021уч.год.

Введение

Если вы любите решать задачи на смекалку или головоломки, то, наверное, составляли таблицы, изображали объекты точками, соединяли их отрезками или стрелками, выполняли над точками и отрезками операции, не похожие на арифметические, алгебраические или геометрические преобразования, то есть вам приходилось строить математический аппарат специально для решения задачи. А это означает, что вы заново открывали для себя начала теории графов.

Впервые с задачами, для решения которых используются графы, я встретилась на олимпиаде по математике. Трудности в решении этих задач объяснялись отсутствием этой темы в обязательном курсе школьной программы. Возникшая проблема стала главной причиной выбора темы данной исследовательской работы.

Цели и задачи: Познакомиться с понятием “граф”, с его основными элементами: вершина, ребра. Научиться составлять и читать графы по словесному описанию отношений между предметами и существами. Развить логическое и образное мышление, воображение. Показать связь с другими областями знаний. Исследовать роль графов в нашей жизни. Научиться решать задачи при помощи графов. Актуальность и новизна: Теория графов находит применение в различных областях современной математики и ее многочисленных приложениях. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Гипотеза: Если изучить теорию графов, то произойдёт повышение интереса к математике, развитие логического мышления.

История возникновения графов

содержание

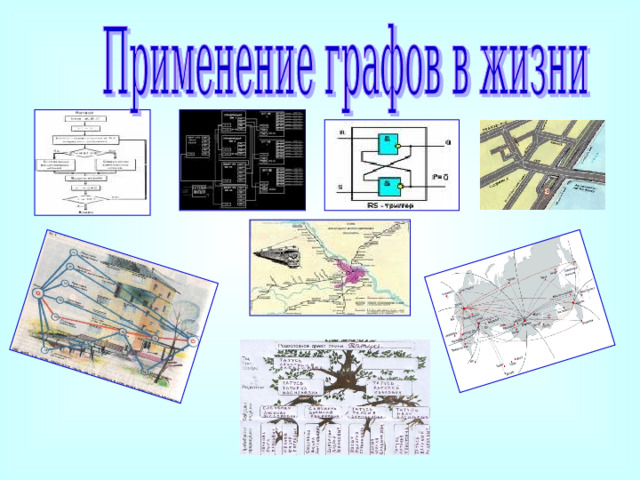
При взгляде на географическую карту сразу бросается в глаза сеть железных дорог. Это типичный граф: кружочки обозначают станции - вершины графа , а соединяющие их пути - ребра.

Инженер чертит схемы электрических цепей. Химик рисует структурные формулы, чтобы показать, как в сложной молекуле с помощью валентных связей соединяются друг с другом атомы. Историк прослеживает родословные связи по генеалогическому дереву. Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление. Социолог на сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпорации.

Что общего во всех этих примерах? В каждом из них фигурирует схема, состоящая из точек (они обозначают разветвления электрической цепи, атомы, людей, города и т.д.), соединённых между собой линиями.

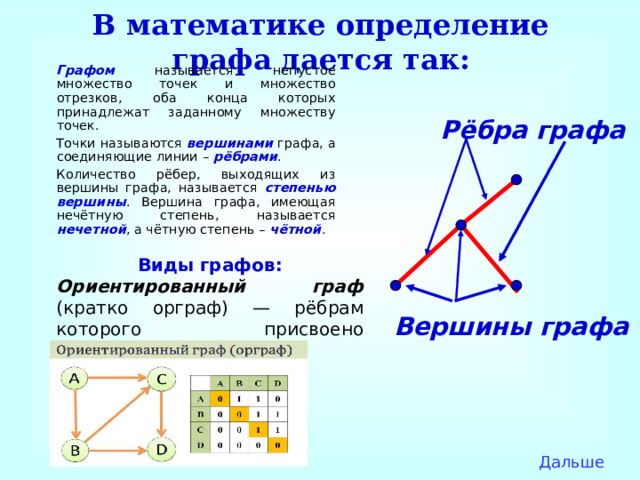
В математике определение графа дается так:

Графом называется непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

Точки называются вершинами графа, а соединяющие линии – рёбрами .

Количество рёбер, выходящих из вершины графа, называется степенью вершины . Вершина графа, имеющая нечётную степень, называется нечетной , а чётную степень – чётной .

Рёбра графа

Виды графов:

Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.

Вершины графа

Дальше

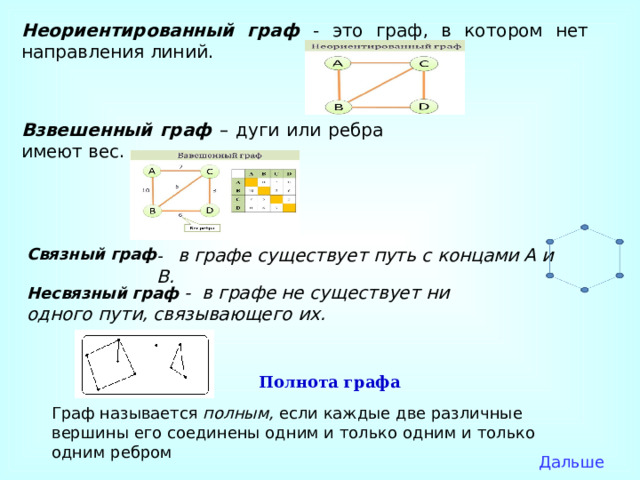
Несвязный граф - в графе не существует ни одного пути, связывающего их.

Граф называется полным, если каждые две различные вершины его соединены одним и только одним и только одним ребром

Неориентированный граф - это граф, в котором нет направления линий.

Взвешенный граф – дуги или ребра имеют вес.

Связный граф

- в графе существует путь с концами А и В.

Полнота графа

Дальше

Эйлеров граф

Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым .

Решая задачу о кенигсбергских мостах, Эйлер сформулировал свойства графа:

• Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
• Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
• Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
• Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.

дальше

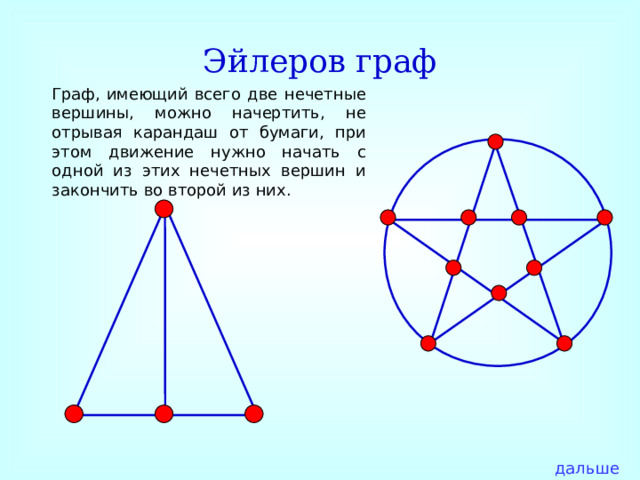
Эйлеров граф

Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.

дальше

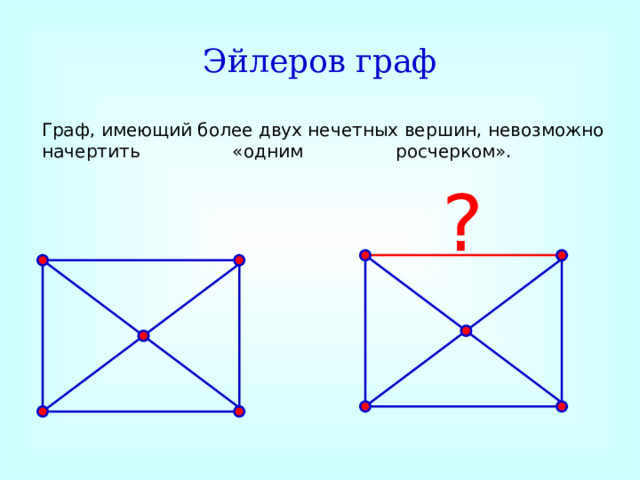
Эйлеров граф

Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».

?

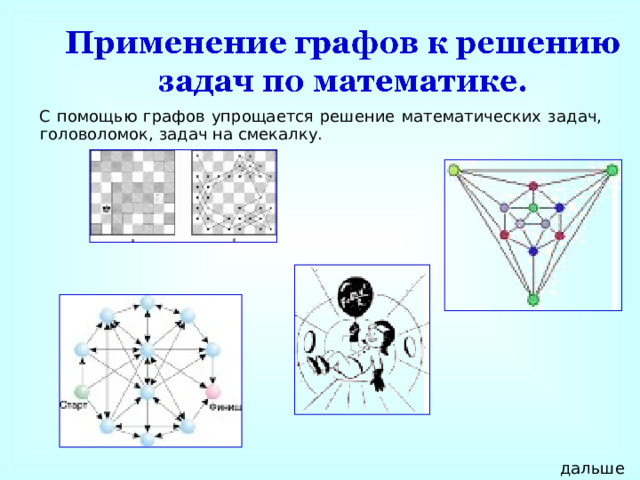
С помощью графов упрощается решение математических задач, головоломок, задач на смекалку.

дальше

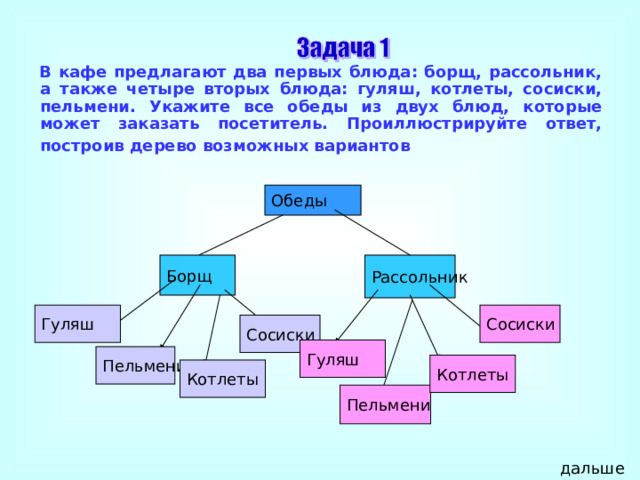
В кафе предлагают два первых блюда: борщ, рассольник, а также четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель. Проиллюстрируйте ответ, построив дерево возможных вариантов

Обеды

Рассольник

Борщ

Гуляш

Сосиски

Сосиски

Гуляш

Пельмени

Котлеты

Котлеты

Пельмени

дальше

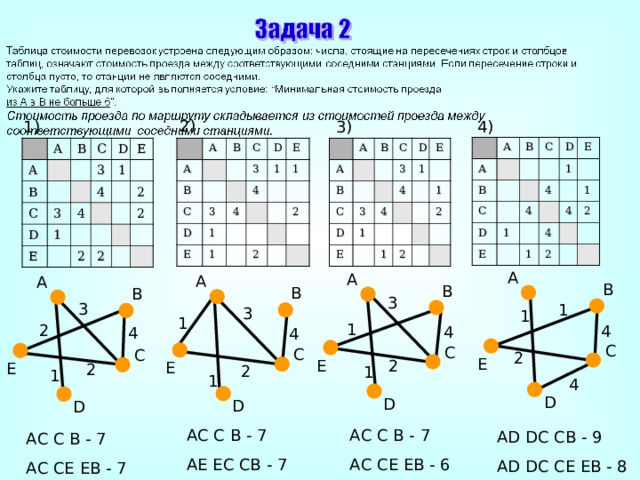
2)

1)

4)

3)

A

A

B

B

C

C

D

D

1

Е

Е

4

1

4

4

4

1

1

2

2

A

A

A

A

A

A

B

B

B

B

B

B

C

C

C

C

C

C

3

3

3

3

3

3

D

D

D

D

D

D

4

4

1

Е

1

Е

4

1

4

Е

1

Е

1

Е

4

1

4

Е

1

1

2

1

2

1

2

2

2

2

2

2

A

A

A

A

B

B

B

B

3

3

1

3

1

1

1

2

4

4

4

4

C

C

C

C

2

E

E

2

E

E

2

2

1

1

1

4

D

D

D

D

AC C B - 7

AC CE EB - 6

AC C B - 7

AE EC CB - 7

AD DC CB - 9

AD DC CE EB - 8

AC C B - 7

AC CE EB - 7

15

На шахматной мини-доске (рис.1) размером 3х3 расположены четыре коня – два белых и два черных. Задача – переставить фигуры так, чтобы одинаковые кони оказались в противоположных углах доски (рис. 2 ). Перемешать их можно только ходом шахматного коня и нельзя ставить фигуру на уже занятое поле.

Все попытки совершить такую перестановку терпят неудачу. Почему?

• Давайте начертим граф возможных ходов коней на доске (рис. 3 ). Затем построим изоморфный ему граф без самопересечений в двух вариантах: на одном отметим первоначальное положение коней, а на другом – требуемое (рис. 4 ,а, б). Вот теперь понятно, почему задача не решается. Движение коней по графу означает переходы в соседние вершины, и перейти из первой позиции во вторую невозможно без «перескока» через коня другого цвета .

дальше

Пусть на столе лежит 5 спичек. Двое игроков по очереди берут 1 или 2 спички. Выигрывает тот, кто забирает последнюю.

Нарисуем граф всевозможных продолжений игры .Видно, что после первого хода на столе остается 3 или 4 спички. Если тот, кто начинает, оставит на столе 3 спички, то он выиграет: ведь его партнер вынужден будет оставить 1 или 2 спички, которые начинавший и заберет на следующем ходу. Если же начинающий игру оставит 4 спички, то он проиграет, так как партнер, взяв 1 спичку, оставит ему 3, что, как мы уже видели, ведет к проигрышу игрока, делающего очередной ход. Конечно же, второй игрок может оставить 2 спички и тут же проиграть, но это маловероятно. Можно сделать вывод: начинающий проигрывает, если исходное число спичек делится на 3, и выиграет в остальных случаях, оставляя партнеру всякий раз количество спичек, которое делится на три

дальше

Два игрока играют в следующую и. Перед ними лежат две кучки камней, в первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

3,2, ∑ 5

1 ход

1 игрок

3,6, ∑ 9

9,2, ∑ 11

3,3, ∑ 6

3,3, ∑ 6

4,2, ∑ 6

2 ход

2 игрок

3,4, ∑ 7

3,9, ∑ 12

12,2, ∑ 14

3,18, ∑ 21

27,2, ∑ 29

4,3, ∑ 7

5,2, ∑ 7

4,6, ∑ 10

Правильное указание выигрывающего игрока и его ходов со строгим доказательством правильности (с помощью дерева игры)

Оценивается максимальным кол-вом баллов.

Выигрывает второй игрок.

Для доказательства рассмотрим неполное дерево игры

Числа соответствуют количеству камней на каждом этапе игры, в первой и второй кучах соответственно и их сумма.

Второй игрок выигрывает на четвертом ходу, после любого ответа первого игрока.

Дерево содержит все возможные варианты ходов первого игрока. Из него видно,

что при любом ходе первого игрока у второго имеется ход, приводящий к победе.

3 ход

1 игрок

12,3, ∑ 15

4,9, ∑ 13

5,3, ∑ 8

4,4, ∑ 8

4 ход

2 игрок

36,3, ∑ 39

15,3, ∑ 18

4,27, ∑ 31

13,3, ∑ 16

12,9, ∑ 21

12,9, ∑ 21

12,4, ∑ 16

12,4, ∑ 16

18

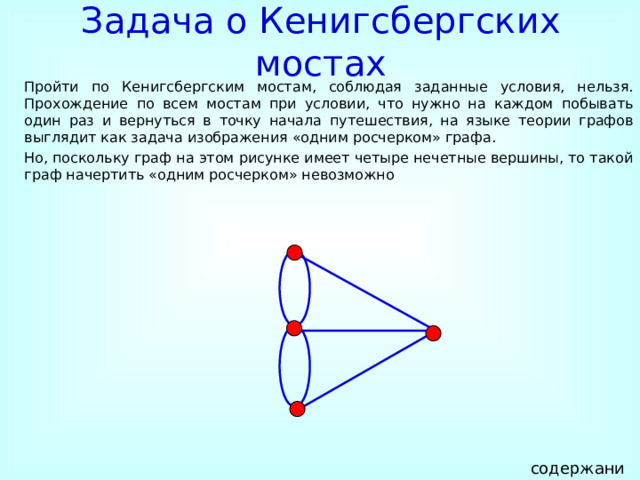
Задача о Кенигсбергских мостах

Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.

Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно

содержание

Заключение.

Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. Я исследовала только самые основные понятия, свойства графов и некоторые способы решения задач . Язык графов прост, доступен и понятен. Графовые задачи обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления детей. Они допускают изложения в занимательной, игровой форме. С другой стороны, они труднее поддаются формализации, чем например, школьные задачи по алгебре, для их решения часто не требуется глубоких знаний, а следует применить смекалку.

Выполняя данный проект я сделала вывод, что графы во многом облегчают нашу жизнь. Это относится не только о их применении в школе, но и в реальной жизни.

• Оре Ойстин «Графы и их применение» М, 1965
• Липатов Е. П. «Теория графов и её применение», 1986
• Берж К. «Теория графов и её применение», 1962
• Верезина Л.Ю. «Графы и их применение», 1979
• Оре Ойстин «Теория графов», 1980
• Уилсон Р. «Введение в теорию графов», 1977
• Зыков Л.А. «Основа теории графов», 1987

Список онлайн-ресурсов.

1.https://globallab.org/ru/project/cover/reshenie_zadatch_s_pomoshju_grafa.ru.html#.WgAagF27WUl

2.https://infourok.ru/issledovatelskaya_rabota_po_matematike_grafy_i_ih_primenenie-300803.htm

3.https://infourok.ru/nauchnoissledovatelskaya-rabota-po-matematike-na-temu-grafi-414185.html

4.https://ru.wikipedia.org/wiki/Граф_(математика)

5.https://infourok.ru/issledovatelskaya_rabota_po_teme_reshenie_olimpiadnyh_zadach_s_pomoschyu_6.grafov-294265.htm

7.https://globallab.org/ru/project/cover/reshenie_zadatch_s_pomoshju_grafa.ru.html#.WlsXpTeWSUm

18