Методическая разработка: "Использование компьютерной программы GeoGebra на уроках математики
при изучении тем: "Неравенства с одной переменной второй степени " и "Уравнения и неравенства с двумя переменными".
1.Введение.
В 9-ом классе начинается изучение тем: "Неравенства с одной переменной второй степени " и "Уравнения и неравенства с двумя переменными". Данные темы рассматриваются в учебнике по алгебре, например: Алгебра. 9 класс: учеб. для общеобразовательных организаций/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова/; под. ред. С.А. Теляковского. - 21 изд. - М,: Просвещение, 2014.- 271с. По мнению многих преподавателей - математиков, и моему мнению, данные темы с трудом усваиваются обучающимися. Почему дело обстоит именно так? Я думаю, что упускаются некоторые аспекты в изучении этих тем.
Решение задач является важнейшим видом учебной деятельности, в процессе которой учащимися усваивается математическая теория и развиваются логическое мышление и творческие способности. Развитие творческих способностей учащихся при обучении математики осуществляется более эффективно при вовлечении в их деятельность различных компьютерных программ и математических пакетов. Одним из таких математических пакетов является - GEOGEBRA.
При помощи этой программы я подробно разберу данные темы и покажу наглядные методы решений.
2.Математический пакет GEOGEBRA
GeoGebra – это свободная образовательная математическая программа, соединяющая в себе геометрию, алгебру и математические исчисления. GeoGebra – свободно-распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать «живые чертежи» в планиметрии, в частности, для построений с помощью циркуля и линейки. Кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка (который, кстати, позволяет управлять и геометрическими построениями). Программа написана Маркусом Хохенвартером на языке Java (соответственно работает медленно, но на большинстве операционных систем). Переведена на 39 языков. Полностью поддерживает русский язык.
Программная среда GeoGebra может быть быстро освоена людьми, имеющими элементарные навыки работы на компьютере, что, несомненно, является большим преимуществом данного программного продукта. К еще одному аргументу в пользу GeoGebra можно отнести её простую интеграцию с офисными приложениями – все чертежи легко могут через буфер обмена быть перенесены для дальнейшего использования как в текстовые редакторы, поддерживающие работу с изображениями, так и в графические редакторы. Используя эту математическую программу можно организовывать преподавание математики более увлекательной и запоминающей и при этом упростить некоторые доказательства.
3. Неравенства с одной переменной второй степени.
Уравнения и неравенства с двумя переменными.
Неравенства вида , , ,
где ; - многочлены соответственно степеней n и m, т.е.
обычно решаются методом интервалов.
Отметим , что неравенство ; , равносильно неравенству .
Для того чтобы решить неравенство , необходимо разложит многочлены на множители.
Множеством решения нестрогого неравенства и
является объединение двух множеств: множество решений строгого неравенства и множество решений уравнения
Задача 1
Решить неравенство: ;
Метод интервалов используется для решения неравенств вида:
Где - действительные и различные числа, символ может означать: <, >, ≤, ≥. Обозначим
1. Отметить на числовой оси , разбив ее тем самым на интервал.
2. В самом правом интервале поставить знак «+», так как в нем .
3. Расставить знаки выражения в остальных интервалах, двигаясь справа налево: после «+» - знак «-», затем «+» и т.д. чередуя знаки.
4. Решение неравенства - объединение всех интервалов со знаком «+».Решение неравенства - объединение всех интервалов со знаком«-».
5. Если нужно, учесть, что в точках .
Решение
Вначале необходимо найти нули в левой части данного неравенства ( т.е. те значения x которые обращают многочлен в 0).
Строим числовую прямую и отмечаем точки:
+ - +
-1 1
Ответ: .
Просмотр содержимого документа
«Использование компьютерной динамической программы ГеоГебры при решении неравенств»
Использование компьютерной динамической программы ГеоГебры
при решении неравенств
Разработал: Антипин А.А.
Для наглядности построенных графиков в ГеоГебре необходимо заштриховывать или закрашивать области пересечения графиков и не только. В своей работе я пошагово покажу как это сделать.
Алгоритм выполнения.
1. Открываем ГеоГебру двойным нажатием левой клавишей, появляется окно.
(рис.1)

2. Нажимаем - Алгебра и графики.
(рис.2)
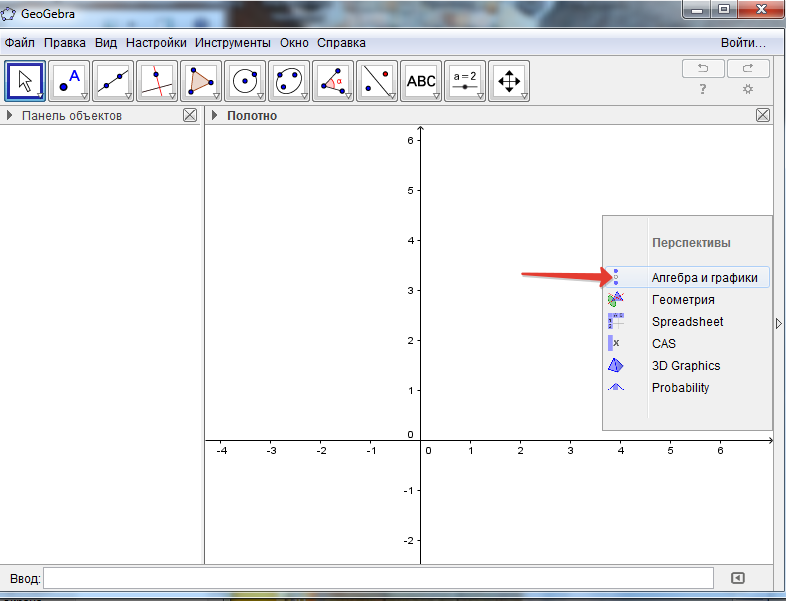
3.В самом низу окна имеется поле для ввода формул. Это красный прямоугольник. В нем имеется кнопочка.
Если нажать на эту кнопочку, появится окошечко с символами. Если навести мышкой на символ выскакивают пояснения к ним.

(рис.3)
4.В поле ввода формул наберите неравенства (обязательно в скобочках) и между скобками поставьте знак, означающий союз «и» (его нужно взять из окошка символов).
(рис.4)
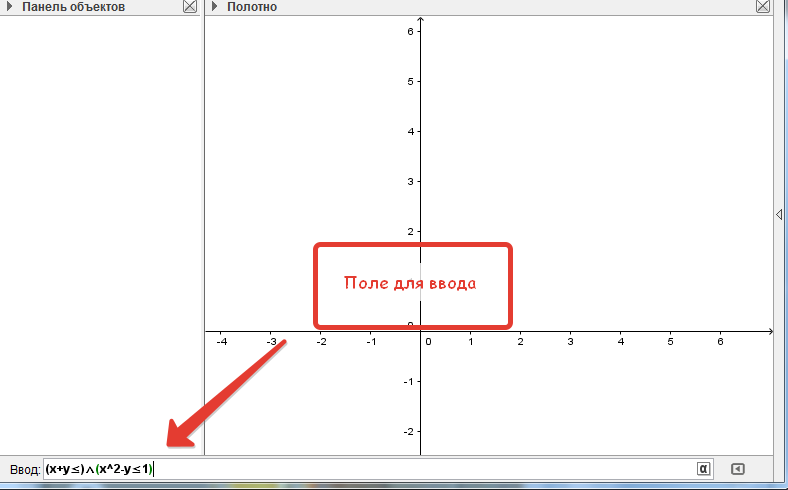 5.Нажмите ENTER.
5.Нажмите ENTER.
(рис.5)
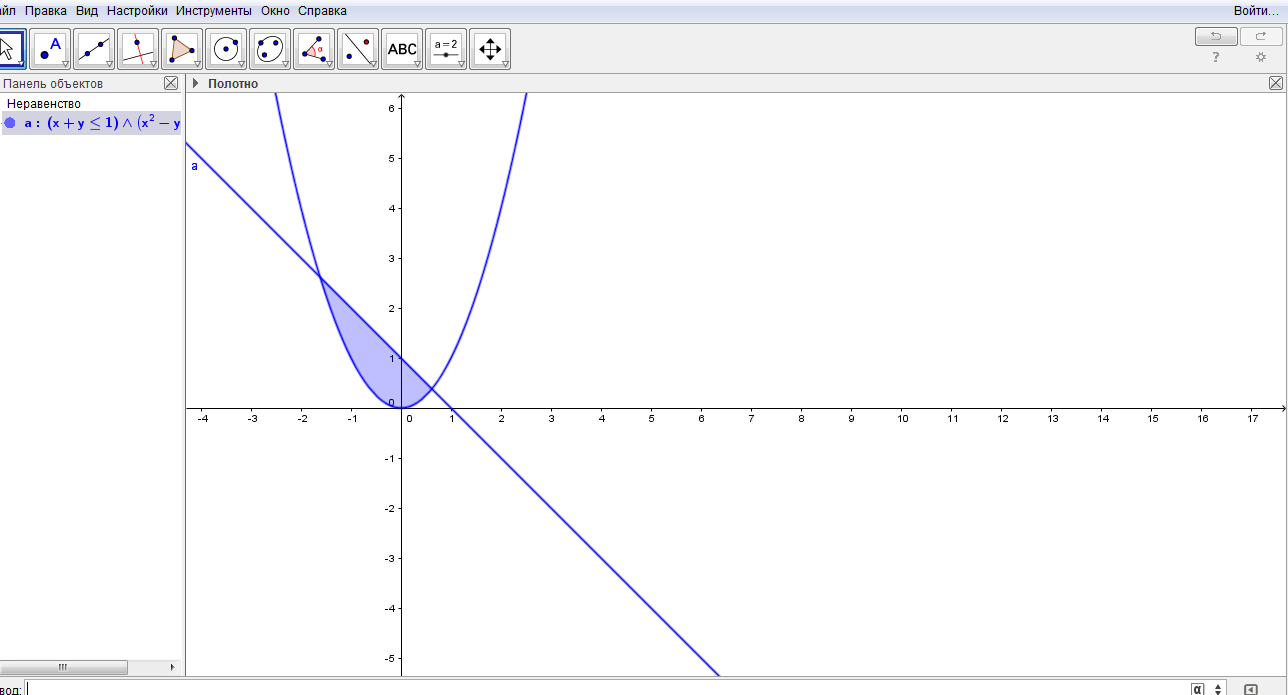
Вот и готов чертеж. Зоны неравенств выделились автоматически Но можно, для наглядности, область пересечения заштриховать. Черные и жирные линии более выразительны. Давайте научимся делать это.
6.На белом фоне кликните мышью и нажмите на правую клавишу мыши. Откроется маленькое окошечко.
(рис.6)

7.Нажимаем Полотно. В открывшемся окне ставьте галочку против Полужирный и нажав против Стиль линии выбираем нужный вид осей координат. Закройте это окно нажав красный крестик справа наверху и увидите такую картинку. (рис.7)

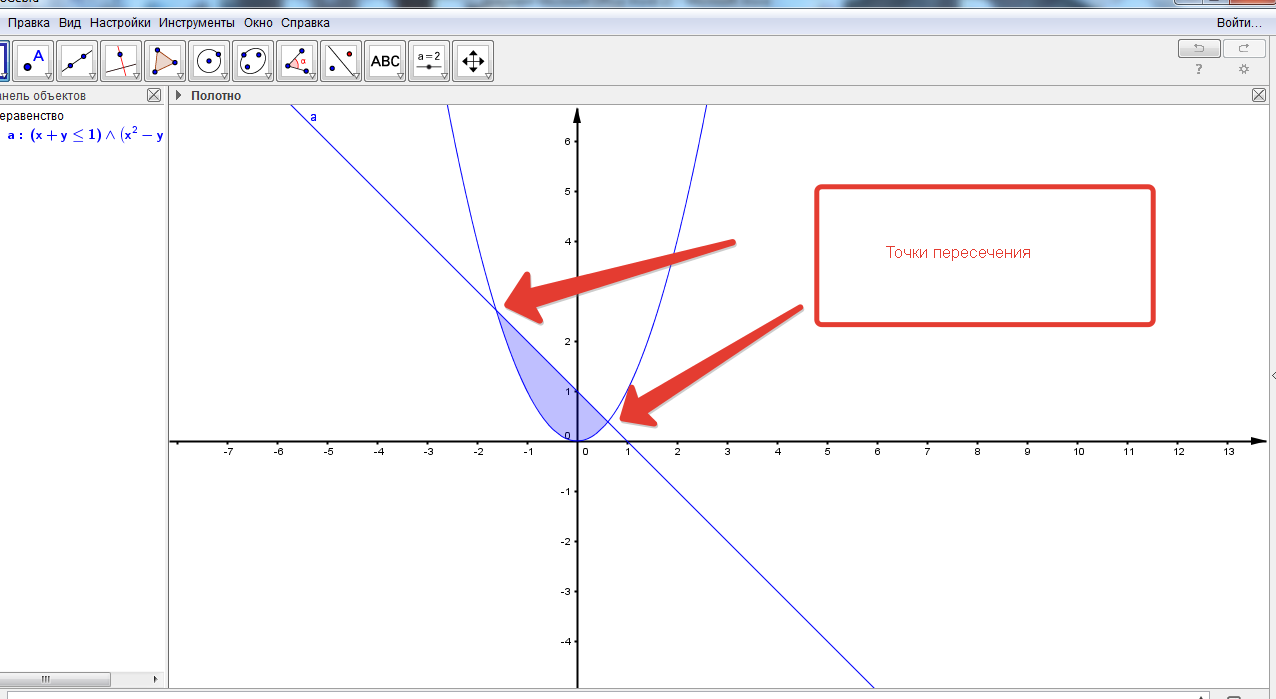
Оси стало лучше видно. (рис.8)
8.Теперь щелкаем мышкой внутри закрашенной области и жмем правую клавишу мыши.
(рис.9)
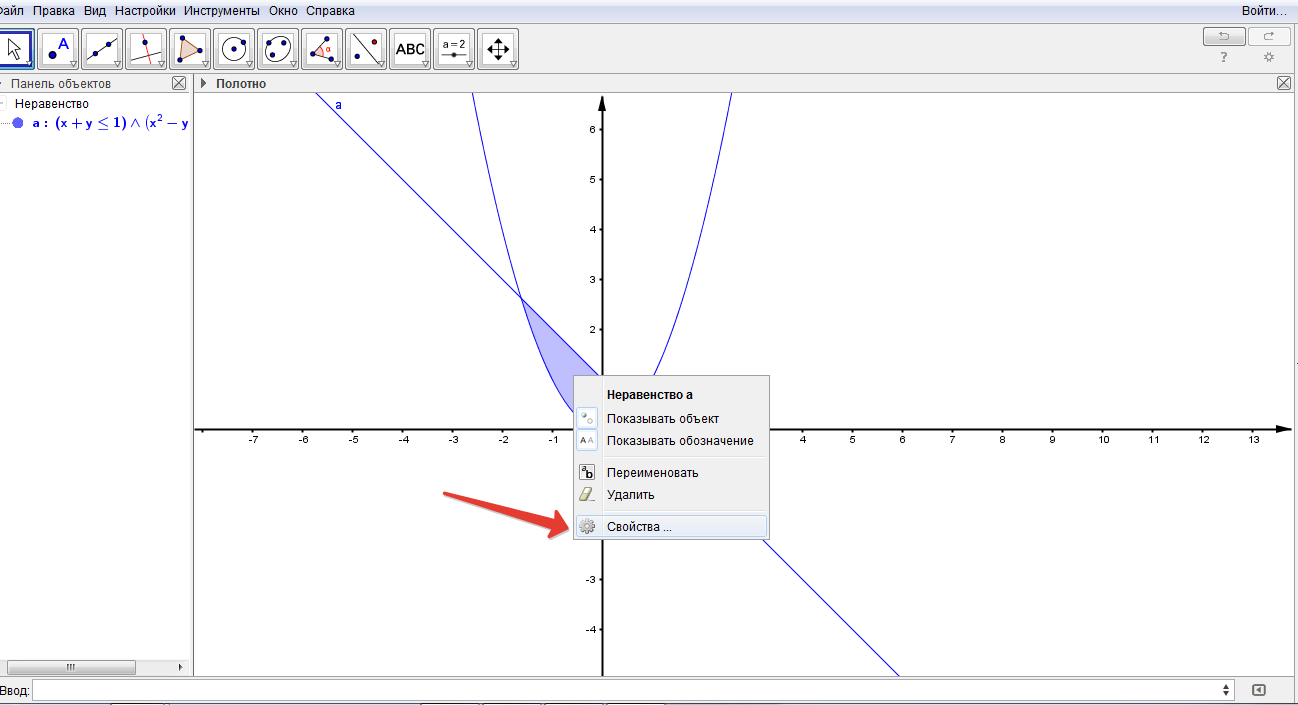
В выпадающем окне нажимаем Свойства. Откроется такое окно.
(рис.10)
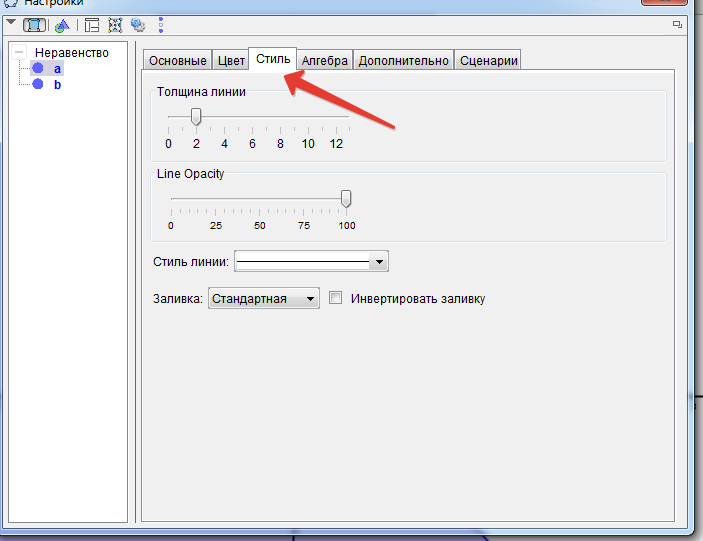
9.В нем нажимаем Стиль. (рис.11)
Мышкой показываем и кликаем на нужную толщину линии. Нажимаем Заливка и выбираем Штриховка.
(рис.12)
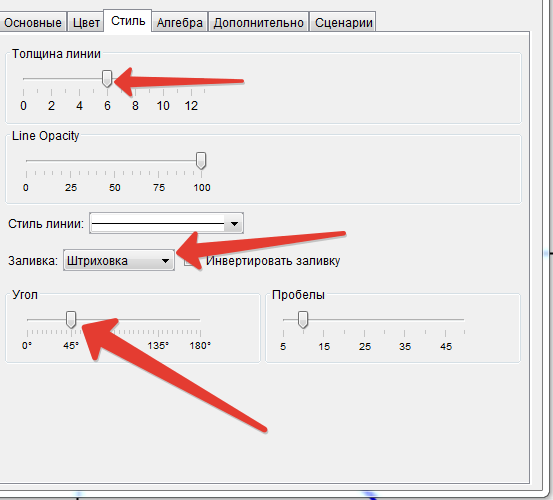
Закрываем это окно.
(рис.13)

В более сложных случаях необходимо пользоваться Виртуальной клавиатурой. В поле ввода формул наберите неравенства (обязательно в скобочках) и между скобками поставьте знак, означающий союз «и» (его нужно взять из окошка символов) используя таблицу символов и виртуальную клавиатуру.(рис.14)
 Нажимаем Полотно. В открывшемся окне ставьте галочку против Полужирный и нажав против Стиль линии выбираем нужный вид осей координат. Закройте это окно нажав красный крестик справа наверху и увидите такую картинку. (рис.15)
Нажимаем Полотно. В открывшемся окне ставьте галочку против Полужирный и нажав против Стиль линии выбираем нужный вид осей координат. Закройте это окно нажав красный крестик справа наверху и увидите такую картинку. (рис.15)
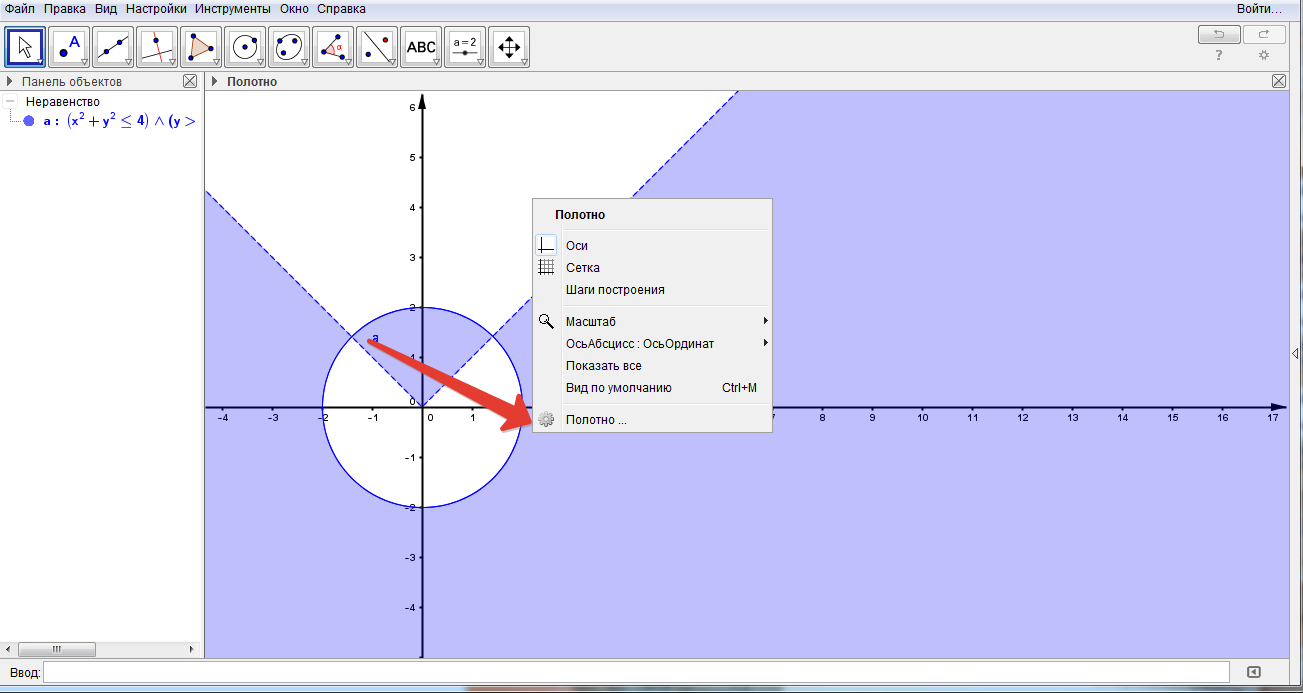

(рис.16)
Области неравенств автоматически закрасятся. Если формулы набрать отдельно, то такой закраски не будет. Это основной нюанс по набору неравенств в Геогебре.
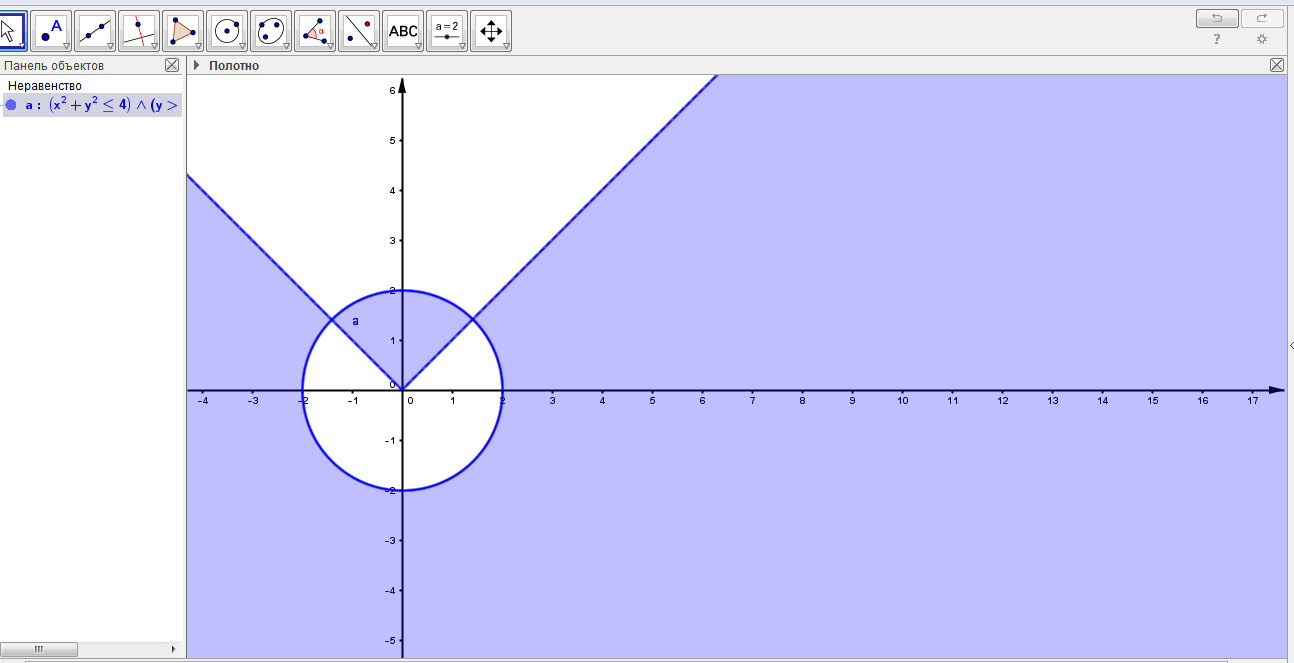










 5.Нажмите ENTER.
5.Нажмите ENTER. 







 Нажимаем Полотно. В открывшемся окне ставьте галочку против Полужирный и нажав против Стиль линии выбираем нужный вид осей координат. Закройте это окно нажав красный крестик справа наверху и увидите такую картинку. (рис.15)
Нажимаем Полотно. В открывшемся окне ставьте галочку против Полужирный и нажав против Стиль линии выбираем нужный вид осей координат. Закройте это окно нажав красный крестик справа наверху и увидите такую картинку. (рис.15)



















