5
Использование методов математической статистики в психолого-педагогических исследованиях
Окружающий нас мир насыщен информацией – разнообразные потоки данных окружают нас, захватывая в поле своего действия, лишая правильного восприятия действительности. Не будет преувеличением сказать, что информация становится частью действительности и нашего сознания. Без адекватных технологий анализа информации (данных) человек оказывается беспомощным в жестокой информационной среде. Статистика позволяет компактно описать данные, понять их структуру, провести классификацию, увидеть закономерности в хаосе случайных явлений.
Для студентов полезно и необходимо знать, где, когда и как методы математической статистики могут применяться на практике для анализа данных психолого-педагогического исследования. Наша цель - максимально развить интуитивное и практическое представление учащихся об анализе данных, статистической обработке педагогического эксперимента, не предполагая наличия у них специальной подготовки. Мы хотим познакомить Вас с культурой анализа данных.
От педагога-исследователя требуются сейчас хорошие знания информатики, основных статистических методов, а также умение ставить и решать исследовательские задачи с использованием ЭВМ.
Широкому внедрению методов анализа данных в 60-х и 70-х годах нашего века немало способствовало появление компьютеров, а начиная с 80-х годов — персональных компьютеров. Статистические программные пакеты сделали методы анализа данных более доступными и наглядными. Теперь уже не требуется вручную выполнять трудоемкие расчеты по сложным формулам, строить вручную сложные диаграммы и графики — всю эту черновую работу взял на себя компьютер, а исследователю осталась главным образом творческая работа: постановка задач исследования, выбор методов педагогического исследования и грамотная интерпретация результатов.
Приведем несколько примеров применения методов анализа данных в практических задачах.
Пример 1. Рассмотрим довольно часто встречающуюся задачу. Предположим, что Вы изобрели важное нововведение: изменили систему оплаты труда, перешли на выпуск новой продукции, использовали новую технологию, методику. Вам кажется, что это дало положительный эффект, но действительно ли это так? А может быть этот кажущийся эффект определен вовсе не вашим нововведением, а естественной случайностью, и уже завтра Вы можете получить прямо противоположный, но столь же случайный эффект? Для решения этой задачи надо сформировать два набора чисел, каждый из которых содержит значения интересующего вас показателя эффективности до и после нововведения. Статистические критерии сравнения двух выборок покажут Вам, случайны или неслучайны различия этих двух рядов чисел.
Пример 2. Другая важная задача состоит в прогнозировании будущего поведения некоторого временного ряда: изменения курса доллара, цен и спроса на продукцию или сырье. Для такого временного ряда с помощью статистических методов подбирают некоторое аналитическое уравнение – строят регрессионную модель. Если мы предполагаем, что на интересующий нас показатель влияют некоторые другие факторы, их тоже можно включить в модель, предварительно проверив значимость этого влияния. Затем на основе построенной модели можно сделать прогноз и указать его точность.
Пример 3. Еще одна интересная и часто встречающаяся задача связана с классификацией объектов. Пусть, например, Вы являетесь начальником кредитного отдела банка. Столкнувшись с невозвратом кредитов, Вы решаетесь впредь выдавать кредиты лишь фирмам, которые «схожи» с теми, которые себя хорошо зарекомендовали, и не выдавать тем, которые «схожи» с неплательщиками или мошенниками. Для классификации фирм можно собрать показатели их деятельности (размер основных фондов, валюту баланса, вид деятельности, объем реализации и т.д.), и провести кластерный анализ (многомерное шкалирование) этих данных. Во многих случаях имеющиеся объекты удается сгруппировать в несколько групп (кластеров), и Вы сможете увидеть, не принадлежит ли запрашивающая кредит фирма к группе неплательщиков.
Пример 4. Пусть у вас имеются данные о минеральной воде, поступившей из различных источников: энергетическая ценность, состав, цвет, содержание других веществ, стоимость доставки. И вы хотите определить наиболее ценную по свойствам и более дешевую по себестоимости минеральную воду. Решить данную задачу можно также с помощью методов математической статистики (кластерный анализ).
Все приведенные примеры имеют одну общую черту: непредсказуемость результатов для действий, которые проводятся в неизменных условиях. Еще одной особенностью приведенных примеров является сравнительно малый объем исходных данных (объем выборки). Причина этого состоит в том, что для большинства прикладных исследований, особенно в гуманитарных областях, характерны именно небольшие объемы данных (исключение здесь составляет лишь демография и отдельные области медицинской статистики).
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. Определение, сформулированное видными отечественными математиками А.Н. Колмогоровым и Ю.В. Прохоровым.
Математическая статистика исходит из предположения, что наблюдаемая изменчивость окружающего мира имеет два источника:
– действие известных причин и факторов. Они порождают изменчивость, закономерно объяснимую.
- действие случайных причин и факторов. Большинство природных и общественных явлений обнаруживают изменчивость, которая не может быть целиком объяснена закономерными причинами. В таком случае прибегают к концепции случайной изменчивости. Выражение «случайный» в данном контексте означает «подчиняющийся законам теории вероятности».
Проверка психолого-педагогических гипотез и моделей является тоже случайным событием, так как результаты педагогического исследования определяются очень большим количеством заранее непредсказуемых факторов. Определенные закономерности можно выявить только в случае массовых наблюдений вследствие закона больших чисел. Закон больших чисел – это объективный математический закон, согласно которому совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Отсюда совершенно очевидным является факт, что педагогические измерения однозначно связаны со статистическими измерениями.
Статистический подход – это выявление закономерной изменчивости на фоне случайных факторов и причин. Методы математической статистики позволяют оценить параметры имеющихся закономерностей, проверить те или иные гипотезы об этих закономерностях.
Аппарат математической статистики является изумительным по мощности и гибкости инструментом для отсеивания закономерностей от случайностей. Педагогу-исследователю обязательно необходимо накапливать информацию об окружающем мире, пытаясь выделить закономерности из случайностей.
1. Основные понятия математической статистики
Исключительно важную роль в анализе многих психолого-педагогических явлений играют средние величины, представляющие собой обобщенную характеристику качественно однородной совокупности по определенному количественному признаку.
В психолого-педагогических исследованиях обычно применяются различные виды средних величин; наиболее распространенными являются средняя арифметическая, медиана и мода.
Средняя арифметическая применяется в тех случаях, когда между определяющим свойством и данным признаком имеется прямо пропорциональная зависимость (например, при улучшении показателей работы учебной группы улучшаются показатели работы каждого ее члена).
Средняя арифметическая представляет собой частное от деления суммы величин на их число и вычисляется по формуле:
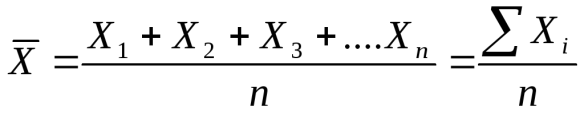 ; (1)
; (1)
где Х - средняя арифметическая; X1, X2, Х3 ... Хn - результаты отдельных наблюдений (приемов, действий),
n - количество наблюдений (приемов, действий),
S - сумма результатов всех наблюдений (приемов, действий).
Медианой (Ме) называется мера среднего положения, характеризующая значение признака на упорядоченной (построенной по признаку возрастания или убывания) шкале, которое соответствует середине исследуемой совокупности. Медиана может быть определена для порядковых и количественных признаков. Место расположения этого значения определяется по формуле: Место медианы = (n + 1) / 2
Например. По результатам исследования установлено, что:
– на «отлично» учатся – 5 человек из участвующих в эксперименте;
– на «хорошо» учатся – 18 человек;
– на «удовлетворительно» – 22 человека;
– на «неудовлетворительно» – 6 человек.
Так как всего в эксперименте принимало участие N = 54 человека, то середина выборки равна 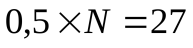 человек. Отсюда делается вывод, что больше половины обучающихся учатся ниже оценки «хорошо», то есть медиана больше «удовлетворительно», но меньше «хорошо» (см. рисунок).
человек. Отсюда делается вывод, что больше половины обучающихся учатся ниже оценки «хорошо», то есть медиана больше «удовлетворительно», но меньше «хорошо» (см. рисунок).
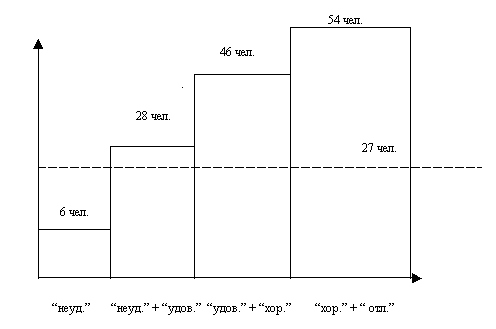 Мода (Мо) – наиболее часто встречающееся типичное значение признака среди других значений. Она соответствует классу с максимальной частотой. Этот класс называется модальным значением.
Мода (Мо) – наиболее часто встречающееся типичное значение признака среди других значений. Она соответствует классу с максимальной частотой. Этот класс называется модальным значением.
Например.
Если на вопрос анкеты: «укажите степень владения иностранным языком», ответы распределились:
1 – владею свободно – 25
2 – владею в достаточной степени для общения – 54
3 – владею, но испытываю трудности при общении – 253
4 – понимаю с трудом – 173
5 – не владею – 28
Очевидно, что наиболее типичным значением здесь является – «владею, но испытываю трудности при общении», которое и будет модальным. Таким образом, мода равна – 253.
Важное значение при использовании в психолого-педагогическом исследовании математических методов уделяется расчету дисперсии и среднеквадратических (стандартных) отклонений.
Дисперсия равна среднему квадрату отклонений значения варианты от среднего значения. Она выступает как одна из характеристик индивидуальных результатов разброса значений исследуемой переменной (например, оценок учащихся) вокруг среднего значения. Вычисление дисперсии осуществляется путем определения: отклонения от среднего значения; квадрата указанного отклонения; суммы квадратов отклонения и среднего значения квадрата отклонения (см. табл. 6.1)1.
Значение дисперсии используется в различных статистических расчетах, но не имеет непосредственного наблюдаемого характера. Величиной, непосредственно связанной с содержанием наблюдаемой переменной, является среднее квадратическое отклонение
Среднее квадратичное отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле:
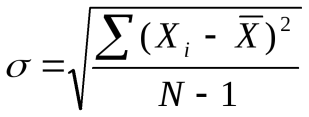 ; (2)
; (2)
где: s – средняя квадратическая. При малом числе наблюдения (действий) – менее 100 – в значении формулы следует ставить не «N», а «N – 1».
Средняя арифметическая и средняя квадратическая являются основными характеристиками полученных результатов в ходе исследования. Они позволяют обобщить данные, сравнить их, установить преимущества одной психолого-педагогической системы (программы) над другой.
Среднее квадратическое (стандартное) отклонение широко применяется как мера разброса для различных характеристик.
Оценивая результаты исследования важно определить рассеивание случайной величины около среднего значения. Это рассеивание описывается с помощью закона Гауса (закона нормального распределения вероятности случайной величины). Суть закона заключается в том, что при измерении некоторого признака в данной совокупности элементов всегда имеют место отклонения в обе стороны от нормы вследствие множества неконтролируемых причин, при этом, чем больше отклонения, тем реже они встречаются.
При дальнейшей обработке данных могут быть выявлены: коэффициент вариации (устойчивости) исследуемого явления, представляющий собой процентное отношение среднеквадратического отклонения к средней арифметической; мера косости, показывающая, в какую сторону направлено преимущественное число отклонений; мера крутости, которая показывает степень скопления значений случайной величины около среднего и др. Все эти статистические данные помогают более полно выявить признаки изучаемых явлений.
Меры связи между переменными. Связи (зависимости) между двумя и более переменными в статистике называюткорреляцией. Она оценивается с помощью значения коэффициента корреляции, который является мерой степени и величины этой связи.
Коэффициентов корреляции много. Рассмотрим лишь часть из них, которые учитывают наличие линейной связи между переменными. Их выбор зависит от шкал измерения переменных, зависимость между которыми необходимо оценить. Наиболее часто в психологии и педагогике применяются коэффициенты Пирсона и Спирмена.
Рассмотрим вычисление значений коэффициентов корреляции на конкретных примерах.
Пример 1. Пусть две сравниваемые переменные X (семейное положение) и Y (исключение из университета) измеряются в дихотомической шкале (частный случай шкалы наименований). Для определения связи используем коэффициент Пирсона.
В тех случаях, когда нет необходимости подсчитывать частоту появления различных значений переменных X и Y, удобно проводить вычисления коэффициента корреляции с помощью таблицы сопряженности (см. табл. 6.2, 6.3, 6.4)1, показывающей количество совместных появлений пар значений по двум переменным (признакам). А – количество случаев, когда переменная X имеет значение равное нулю, и, одновременно переменная Y имеет значение равное единице; В – количество случаев, когда переменные X и Y имеют одновременно значения, равные единице; С – количество случаев, когда переменные X и Y имеют одновременно значения равные нулю; D – количество случаев, когда переменная X имеет значение, равное единице, и, одновременно, переменная Y имеет значение, равное нулю
Пример: Наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Среднее значение посещаемости в обоих классах получается одинаковое - 19. Однако видно, что в контрольном классе этот показатель подчинен воздействию каких-то специфических факторов.
Выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0. Формально это записывается следующим образом:
(`х - х1) + (`х - х2) + ... + (`х - хn) =0
Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.
Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году. Выборочная дисперсия вычисляется по формуле:
s2 = 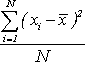 (2)
(2)
где `х — выборочное среднее,
N — число наблюдений в выборке.
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.
Стандартное отклонение, среднее квадратическое отклонение (от английского standard deviation) вычисляется как корень квадратный из дисперсии. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
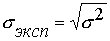 (3)
(3)
Пример: Для предыдущего случая имеем
| Классы | 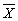
| 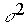
| 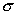
|
| Экспериментальный контрольный | 19 19 | 1 48,5 | 1 8 |
Это означает, что в одном классе посещаемость высокая, стабильная, а в другом - отличается непостоянством.
Медиана разбивает выборку на две равные части. Половина значений переменной лежит ниже медианы, половина — выше. Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр. В некоторых случаях, например при описании доходов населения, медиана более удобна, чем среднее.
Рассмотрим способы определения медианы при различных значениях N. Для нахождения медианы измерения записывают в ряд по возрастанию значений. Если число измерений N нечетное, то медиана численно равна значению этого ряда, стоящему точно в середине, или на (N+1)/2 месте. Например, медиана пяти измерений: 10, 17, 21, 24, 25 – равна 21 – значению, стоящему на третьем месте (N+1)/2=(5+1)/2=3.
Если число измерений четное, то медиана численно равна среднему арифметическому значений ряда, стоящих в середине, или на N/2 и N/2+1 местах. Например, медиана восьми измерений: 5, 5, 6, 7, 8, 8, 9, 9 – равна 7,5 (7+8)/2=7,5 – среднему арифметическому значений ряда, стоящих на четвертом и пятом местах (N/2=8/2=4 и N/2+1=4+1=5).
Квартили представляют собой значения, которые делят две половины выборки (разбитые медианой) еще раз пополам (от слова кварта — четверть).
Различают верхнюю квартиль, которая больше медианы и делит пополам верхнюю часть выборки (значения переменной больше медианы), и нижнюю квартиль, которая меньше медианы и делит пополам нижнюю часть выборки.
Нижнюю квартиль часто обозначают символом 25%, это означает, что 25% значений переменной меньше нижней квартили.
Верхнюю квартиль часто обозначают символом 75%, это означает, что 75% значений переменной меньше верхней квартили.
Таким образом, три точки — нижняя квартиль, медиана и верхняя квартиль - делят выборку на 4 равные части.
¼ наблюдений лежит между минимальным значением и нижней квартилью, ¼ - между нижней квартилью и медианой, ¼ - между медианой и верхней квартилью, ¼ - между верхней квартилью и максимальным значением выборки.
Мода представляет собой максимально часто встречающееся значение переменной (иными словами, наиболее «модное» значение переменной), например, популярная передача на телевидении, модный цвет
платья или марка автомобиля и т. д, Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).
Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»)
Статистика занимается сбором, представлением (в виде таблиц, диаграмм, графиков), анализом информации о количественных характеристиках событий, явлений и совокупностей объектов
3 Например, Монеты можно сравнивать по номиналу, диаметру, весу Юношей одного класса – по росту, весу, возрасту. Например, Монеты можно сравнивать по номиналу, диаметру, весу Юношей одного класса – по росту, весу, возрасту. Генеральная совокупность – вся совокупность данных. Выборка – любая выбранная часть. Репрезентативная выборка – если данные находятся примерно в той же пропорции, что и в генеральной совокупности (устно), 402. Генеральная совокупность – вся совокупность данных. Выборка – любая выбранная часть. Репрезентативная выборка – если данные находятся примерно в той же пропорции, что и в генеральной совокупности (устно), 402.
4 Генеральные совокупности и выборки иногда приходится характеризовать одним числом. К таким характеристикам относятся: 1.Среднее арифметическое (или просто среднее) 2.Размах ряда 3.Мода ряда 4.Медиана ряда
5 среднее арифметическое набора чисел это сумма всех чисел в этом наборе, делённая на их количество. Для трёх чисел сложим их и поделим на 3:
6 Размах ряда – это разница между наибольшим и наименьшим значением Например: 12, 2, 11, 3, 7, 10, 3, 15. Наибольшее =15 Наименьшее = 2 Размах R = 15-2 = 13
7 Мода. Если мы выстроим все пары обуви на складе по цвету, то самый ходовой цвет будет модой. Мода - это то, что непременно должны учитывать производители
8 В совокупности: 2, 3, 3, 4, 5 модой является число 3. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; здесь две моды = 6 и 9). Ряд может иметь две моды, а может не иметь моды. 59,68,66,70,67,71,74 – этот ряд не имеет моды.
9 Если расставить выборку по возрастанию (или убыванию), то медиана - это то, что будет ровно посередине "строя". Например, если мы расположим по порядку длительности интервалы времени: секунда, минута, час, сутки и неделя – то медианой будет час.
10 Производство пшеницы в России в гг. млн.тонн год производство 30,134,944,327,031,034,547,0 Средний урожай равен Найдем медиану: 27,0; 30,1; 31,0; 34,5; 34,9; 44,3; 47,0 30,1; 31,0; 34,5; 34,9; 44,3; 31,0; 34,5; 34,9; 34,5 млн. тонн - медиана
11 Найти медиану набора 12, 2, 11, 3, 7, 10, 3, 15. Расположим числа по возрастанию: 2, 3, 3, 7, 10, 11, 12, 15. Будем убирать одновременно с обоих концов набора числа. Получим последовательные наборы: 2, 3, 3, 7, 10, 11, 12, 15 3, 3, 7, 10, 11, 12 3, 7, 10, 11 7, 10 Медианой в этом случае служит полусумма чисел 7 и 10, т.е. среднее арифметическое. 8,5 – медиана набора.
12 Попробуем найти все характеристики: 26, 23, 18, 25, 20, 25, 30, 25, 34, 19. ( ): 10 = 245:10 = 24,5 – среднее арифметическое = 16 – размах, 25 – мода, Выстроим по возрастанию: 18, 19, 20, 23, 25, 25, 25, 26, 30, – медиана.
13Задания ГИА 1)На соревнованиях по прыжкам в высоту среди девочек 14 лет были показаны результаты: 100; 140; 130; 80; 110; 130; 120; 125; 140; 125; 140; 80. Найдите среднее арифметическое и медиану этого набора чисел. 2)Учащиеся класса за контрольную работу по алгебре получили оценки: 3; 4; 4; 4; 2; 5; 5; 5; 3; 3; 4; 3; 3; 5; 4. Найдите разницу между модой т средним арифметическим этого ряда.
1)На соревнованиях по прыжкам в высоту среди девочек 14 лет были показаны результаты: 100; 140; 130; 80; 130; 130; 120; 125; 140; 125; 140; 80. Найдите среднее арифметическое и медиану этого набора чисел. среднее арифметическое ( ) : 12 = 1440:12 =120 80; 80; 100; 120; 125; 125; 130; 130; 130; 140; 140; 140; Медиана = ( ) : 2 = 127,5 ОТВЕТ: 120; 127,5 среднее арифметическое ( ) : 12 = 1440:12 =120 80; 80; 100; 120; 125; 125; 130; 130; 130; 140; 140; 140; Медиана = ( ) : 2 = 127,5 ОТВЕТ: 120; 127,5
2)Учащиеся класса за контрольную работу по алгебре получили оценки: 3; 4; 4; 4; 2; 5; 5; 5; 3; 3; 4; 3; 3; 5; 4. Найдите разницу между модой т средним арифметическим этого ряда. Мода = 4 Среднее арифметическое = 4 – 3,8 = 0,2 ОТВЕТ: 0,2 Мода = 4 Среднее арифметическое = 4 – 3,8 = 0,2 ОТВЕТ: 0,2
Рассматривает примеры совместно с учащимися с оформлением решения на доске.
Пример 1.
Пусть ученик получил в течение первой учебной четверти следующие отметки по алгебре:
5, 2, 4, 5, 5, 4, 4, 5, 5, 5.
Приме №2
Рост учащихся нашего класса
157,165,165,168,165,161,165,160,162,169,171, 170,170,175,173,170,177,182,186,182,160,173, 165,162,174,177.
1) составить ранжированный ряд ;
2) определить средний рост, моду ряда, медиану ряда.
Пример 3
На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки: 5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3.
Вычислить среднее арифметическое оценок.
Пример № 4
Два стрелка сделали 100 выстрелов. Первый выбил 8 очков 40 раз, 9 очков - 10 раз и 10 очков - 50 раз. Второй выбил 8, 9 и 10 очков соответственно - 10, 60 и 30 раз. Какой из стрелков стреляет лучше?
Объем и Размах
| Выборка состоит из элементов x1,x2, ..., xn{{x}_{1}},{{x}_{2}},\ ...,\ {{x}_{n}}x1,x2, ..., xn, попавших в нее. Количество этих элементов (n)\left( n \right)(n) называется объемом выборки. |
Например, в таблице ниже приведен рост игроков сборной по футболу:

Данная выборка представлена 11 элементами Таким образом, объем выборки (n11.
| Разность между максимальным и минимальным значениями элементов выборки называется размахом выборки. Или, размах выборки =xmax−xmin={{x}_{\max }}-{{x}_{\min }}=xmax−xmin |
Размах представленной выборки составляет xmax−xmin=194−176=18{{x}_{\max }}-{{x}_{\min }}=194-176=18xmax−xmin=194−176=18 см.
Среднее арифметическое
Не очень понятно? Давай смотреть на наш пример.

Определите средний рост игроков.
Ну что, приступим? Мы уже разбирались, что x1=183; x2=194; x3=187; ...; x11=181\displaystyle {{x}_{1}}=183;\ {{x}_{2}}=194;\ {{x}_{3}}=187;\ ...;\ {{x}_{11}}=181x1=183; x2=194; x3=187; ...; x11=181; n=11\displaystyle n=11n=11.
Можем сразу смело все подставлять в нашу формулу:
xcp.=x1+x2+x3+...+xn /n
xcp.=183+194+187+181+176+190+189+184+178+179+181 :11=183,8
Таким образом, средний рост игрока сборной составляет 183,8
Ну или вот такой пример:
Ученикам 9 класса на неделю было задано решить как можно больше примеров из задачника. Количество примеров, решенных учениками за неделю, приведены ниже:

Найдите среднее количество решенных задач.
Итак, в таблице нам представлены данные по 20 ученикам. Таким образом, n=20\ n=20n=20. x1=88; x2=90; x3=51; ...; x20=47.\displaystyle {{x}_{1}}=88;\ {{x}_{2}}=90;\ {{x}_{3}}=51;\ ...;\ {{x}_{20}}=47.x1=88; x2=90; x3=51; ...; x20=47. Ну что ж, найдем для начала сумму (общее количество) всех решенных задач двадцатью учениками:
88+90+51+85+58+105+77+89+100+109+77+83+92+77++44+81+50+77+80+47=1560
Теперь можем смело приступать к расчету среднего арифметического решенных задач, зная, что x1+x2+...+xn=1560 n=20:
xcp.=1560 :20=78.
Таким образом, в среднем ученики 9 класса решили по 78 задач.
Вот еще один пример для закрепления.
Пример.
На рынке помидоры реализуются 7 продавцами, причем цены за 1 кг распределены следующим образом (в руб.): 60, 55, 54, 70, 65, 67, 63 Какова средняя цена килограмма помидоров на рынке?
Решение.
Итак, чему в данном примере равно n? Все верно: семь продавцов предлагают семь цен, значит, n=7
xcp.=x1+x2+...+xnn=60+55+54+70+65+67+637=4347=62\displaystyle {{x}_{cp.}}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}}{n}=\frac{60+55+54+70+65+67+63}{7}=\frac{434}{7}=62xcp.=nx1+x2+...+xn=760+55+54+70+65+67+63=7434=62 (рубля)
Ну что, разобрался? Тогда посчитай самостоятельно среднее арифметическое в следующих выборках:
| Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду. |
34; 46; 67; 37; 45; 60\ 5; 4; 7; 9; 10; 12; 17; 8
156; 180; 164; 172
Ответы: 48,17; 9; 168.
Решил? Можем двигаться дальше.
Мода и медиана
Обратимся снова к нашему примеру со сборной по футболу:

Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке? Все верно, это число 181\displaystyle 181181, так как два игрока имеют рост 181\displaystyle 181181 см; рост же остальных игроков не повторяется. Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») - отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны. Ключевое слово СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
| Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания). Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить. |
Ну что, вернемся к нашей выборке футболистов?

Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»! Наведем порядок в ряду? Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому). Вот, что у меня получилось:

Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке. Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное? Все верно – игроков 11\displaystyle 1111, значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке. Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас 11, значит, по краям остается по пять чисел, а рост 183 см будет медианой в нашей выборке. Не так уж и сложно, правда?
А теперь разберем пример с нашими отчаянными ребятами из 9 класса, которые решали примеры в течение недели:

Готов искать в этом ряду моду и медиану?
Для начала, упорядочим этот ряд чисел (расположим от самого маленького числа к самому большому). Получился вот такой вот ряд:

Теперь можно смело определить моду в данной выборке. Какое число встречается чаще других? Все верно, 77Таким образом, мода в данной выборке равна 77.
Моду нашли, теперь можем приступать к нахождению медианы. Но прежде, ответь мне: каков объем рассматриваемой выборки? Посчитал? Все верно, объем выборки равен 20\displaystyle 2020. А 20\displaystyle 2020 – это четное число. Таким образом, применяем определение медианы для ряда чисел с четным количеством элементов. То есть нам надо в нашем упорядоченном ряду найти среднее арифметическое двух чисел, записанных посередине. Какие два числа располагаются посередине? Все верно, 80\displaystyle 8080 и 81\displaystyle 8181!

Таким образом, медианой этого ряда будет среднее арифметическое чисел 80 и 81
80+81:2=161:2=80,580,580,580,5- медиана рассматриваемой выборки.
Частота и относительная частота
| Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины. |
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:

Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост 176176176? Все верно, один игрок. Таким образом, частота встречи игрока с ростом 176176176 в нашей выборке равна 111. Сколько игроков имеет рост 178178178? Да, опять же один игрок. Частота встречи игрока с ростом 178178178 в нашей выборке равна 111. Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:

Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки). То есть в нашем примере: 1+1+1+2+1+1+1+1+1+1=111+1+1+2+1+1+1+1+1+1=111+1+1+2+1+1+1+1+1+1=11
Перейдем к следующей характеристике – относительная частота.
| Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах. |
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем (n=11)\left( n=11 \right)(n=11) . Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:

А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Графическое изображение данных
Очень часто для наглядности данные представляются в виде диаграмм/графиков. Остановимся на рассмотрении основных из них:
столбчатая диаграмма,
круговая диаграмма,
гистограмма,
полигон
Столбчатая диаграмма
Столбчатые диаграммы используют тогда, когда хотят продемонстрировать динамику изменения данных во времени или распределения данных, полученных в результате статистического исследования.
Например, у нас есть вот такие данные об оценках написанной контрольной работы в одном классе:

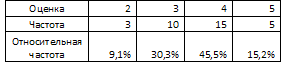
Количество получивших такую оценку – это у нас и есть частота. Зная это, мы можем составить вот такую вот табличку:
Теперь мы можем построить наглядные столбчатые графики на основе такого показателя как частота (на горизонтальной оси отражены оценки (2,3,4,5)\displaystyle \left( 2,3,4,5 \right)(2,3,4,5) на вертикальной оси откладываем количество учеников, получивших соответствующие оценки):
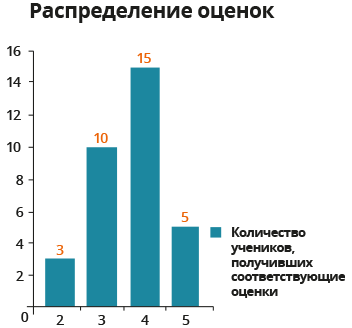
Или же можем построить соответствующий столбчатый график на основе относительной частоты:
Рассмотрим пример по типу задания В3 из ЕГЭ.
Пример.
На диаграмме показано распределение добычи нефти в 7\displaystyle 77 странах мира (в тоннах) за 2011 год. Среди стран первое место по добыче нефти занимала Саудовская Аравия, седьмое место – Объединенные Арабские Эмираты. Какое место занимали США?
Ответ: третье.
Круговая диаграмма
Для наглядного изображения соотношения между частями исследуемой выборки удобно использовать круговые диаграммы.
По нашей табличке с относительными частотами распределения оценок в классе мы можем построить круговую диаграмму, разбив круг на секторы, пропорциональные относительным частотам.
Вот так:
Круговая диаграмма сохраняет свою наглядность и выразительность только при небольшом числе частей совокупности. В нашем случае, таких частей четыре (в соответствии с возможными оценками 2,3,4,5\displaystyle 2,3,4,52,3,4,5), поэтому применение такого типа диаграммы достаточно эффективно.
Пример.
На диаграмме показано распределение расходов семьи во время отдыха на море. Определите, на что семья потратила больше всего?
Ответ: проживание.
Полигон
Динамику изменения статистических данных во времени часто изображают с помощью полигона. Для построения полигона отмечают в координатной плоскости точки, абсциссами которых служат моменты времени, а ординатами – соответствующие им статистические данные. Соединив последовательно эти точки отрезками, получают ломанную, которую называют полигоном.
Вот, к примеру нам даны среднемесячные температуры воздуха в Москве.
Сделаем приведенные данные более наглядными – построим полигон.
На горизонтальной оси отражены месяцы, на вертикальной – температура. Строим соответствующие точки и соединяем их. Вот, что получилось:
Согласись, сразу стало наглядней!
Полигон, используют также для наглядного изображения распределения данных, полученных в результате статистического исследования.
Вот построенный полигон на основе нашего примера с распределением оценок:
На рисунке жирными точками показана цена алюминия на момент закрытия биржевых торгов во все рабочие дни с 7 по 20 августа2014 года. По горизонтали указываются числа месяца, по вертикали — цена тонны алюминия в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена алюминия на момент закрытия торгов была наименьшей за данный период.
Гистограмма
Интервальные ряды данных изображают с помощью гистограммы. Гистограмма представляет собой ступенчатую фигуру, составленную из сомкнутых прямоугольников. Основание каждого прямоугольника равно длине интервала, а высота – частоте или относительной частоте. Таким образом, в гистограмме, в отличие от обычной столбчатой диаграммы, основания прямоугольника выбираются не произвольно, а строго определены длиной интервала.
Вот, к примеру, у нас есть следующие данные о росте игроков, вызванных в сборную:
Итак, нам дана частота (количество игроков с соответствующим ростом). Мы можем дополнить табличку, рассчитав относительную частоту:
Ну вот, теперь можем строить гистограммы. Сначала построим на основании частоты. Вот, что получилось:
А теперь на основании данных об относительной частоте:
На выставку по инновационным технологиям приехали представители 50\displaystyle 5050 компаний. На диаграмме показано распределение этих компаний по количеству персонала. По горизонтали представлено количество сотрудников в компании, по вертикали - количество компаний, имеющих данное число сотрудников.
Какой процент составляют компании с общим числом сотрудников больше 50 5050 человек?
Ответ: 68%
Практические занятия
Студенту необходимо уметь:
-применять математические методы для решения профессиональных задач;
-проводить элементарную статистическую обработку информации и результатов исследований, представлять полученные данные графически.
№ 1-3.Представление данных в виде таблиц, диаграмм, графиков
Выполните следующие задания:
1.Решите задачу (вычислите среднее арифметическое, медиану, размах и моду ряда чисел) и постройте таблицу, диаграмму (круговую и столбчатую), график (гистограмму):
а) Отмечая время, которое учащиеся 3 класса затратили на выполнение практического задания, получили такой ряд данных (в минутах):
20, 18, 21, 19, 14, 17,16, 19,21,21 16, 19,21, 20,18,19, 15, 17, 16, 18, 20.
б) Учащимся 4 класса была предложена контрольная работа по математике, содержащая 5 заданий. При проверке выяснили, что ученики допустили по несколько вычислительных ошибок: 1, 2, 4, 3 ,4, 1, 2, 4 , 5, 7, 8, 5, 1, 2, 1, 3, 1, 0, 4, 2 , 1, 3 , 4.
2. Учащимся одного класса дали задание отметить, сколько минут в определённый день они затратили на дорогу от дома до школы. Получили следующие результаты:
15, 16, 24, 16, 22, 19, 24, 16, 14, 19, 17, 15, 17, 25, 10, 18.
Используя эти данные, составьте интервальный ряд с интервалом в 3 минуты. Постройте соответствующую гистограмму.






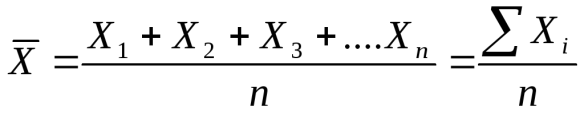 ; (1)
; (1) Мода (Мо) – наиболее часто встречающееся типичное значение признака среди других значений. Она соответствует классу с максимальной частотой. Этот класс называется модальным значением.
Мода (Мо) – наиболее часто встречающееся типичное значение признака среди других значений. Она соответствует классу с максимальной частотой. Этот класс называется модальным значением.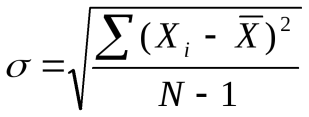 ; (2)
; (2)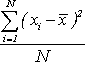 (2)
(2)





















