Министерство образования и науки Республики Бурятия
Муниципальное образование Кяхтинский район
МБОУ Малокударинская СОШ
Исследовательская работа
ЧУДО – КЛЕТКА
Выполнила ученица 9 класса Сметанина Любовь
Руководитель учитель Красикова Татьяна Ильинична
Введение
Клетка – ты Чудо! Загадочна, проста и таинственна.
Сколько возможностей открытий хранишь в себе,
сколько закономерностей можно раскрыть, благодаря этому Чуду.
При подготовке к ОГЭ по математике учитель по математике познакомил нас с различными задачами из базы https://ege.sdamgia.ru/, где одно из заданий будет нахождение площади фигур, высоты, расстояний от заданных точек до прямых по заданным клеткам. Меня заинтересовала данная тема и я решила разобраться в данной теме, так как это интересно и полезно. Обычно для занятий геометрией нужно приготовить много канцелярских принадлежностей: бумагу, карандаш, линейку с делениями, циркуль, транспортир... Оказывается, множество интересных задач можно решать, имея всего лишь линейку без делений, листок клетчатой бумаги и карандаш! Задачи на клетчатой бумаге способствуют развитию интуиции, воображения, внимания, что необходимо в подготовке к математическим олимпиадам, к ОГЭ по математике.
Цель: рассмотреть различные методы решения задач на клетчатой бумаге.
Задачи:
изучить литературу, в поисках различных методов и приёмов решения задач на клетчатой бумаге;
классификации задач на клетчатой бумаге;
научиться выполнять построения, используя «узлы» квадратной сетки;
использовать полученные знания для решения нестандартных задач.
Задачи на клетчатой бумаге способствуют развитию интуиции, воображения, внимания, что необходимо в подготовке к математическим олимпиадам, экзаменам.
На уроке математике не всегда у всех есть под рукой транспортир, но клетчатая бумага (тетрадь) всегда под рукой. Имея ее, мы без труда строим геометрические фигуры, находим расстояния и т.д. Занятия геометрией на клетчатой бумаге создают условия для успешного усвоения геометрического материала.
Некоторые сведения
В голове возникло множество вопросов: почему для построения геометрических фигур удобно использовать клетку? Как помогает тетрадь в клеточку ученику, учителю при решении задач на математике, на других уроках, в окружающем нас мире?
Существует много тетрадей: в кружочек, в ромбик в клеточку, в линеечку и т.д. Но при построениях геометрических фигур мы используем тетрадь в клеточку. Задачи на клетчатой бумаге отличаются от обычных задач из учебника геометрии, и в то же время они не требуют дополнительных сведений, направлены именно на повторение основного курса геометрии 7-9 классов, на его более глубокое освоение и понимание, выработку необходимых навыков. При решении задач применяются геометрические знания в необычной ситуации и вычисления. Все задачи сопровождаются рисунками, которые можно использовать для дополнительных построений и вычислений. Построения отрезков, прямых и углов проводятся с помощью линейки. При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать, как они могут помочь. По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты, связанные с прямоугольным треугольником. Решение таких задач не предполагает использование циркуля и линейки, а осуществляется непосредственно на рисунке клетчатой бумаги. При решении задач ученики часто оказываются в затруднении при встрече с задачами на клетчатой бумаге. Возникли вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. С клетчатой бумагой мы знакомы давно, на многих уроках в школе используем именно тетрадь в клетку. Образована клетка с помощью горизонтальных и вертикальных прямых. Они разбивают плоскость на равные квадраты. Сторону такого квадрата удобно принять за единицу. Вершины этих квадратов, т.е. точки, в которых пересекаются прямые разметки, называются узлами. Из нескольких клеток можно составлять различные фигуры, по клеткам удобно мерить расстояния, разрезать фигуры на равные части.
Квадрат и его свойства.
Клетка в тетрадях по математике является квадратом.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата:
все углы прямые
диагонали равны, взаимно пересекаются, точкой пересечения делятся пополам и делят углы квадрата пополам




А В ABCD - квадрат
АС = ВD – диагонали
О DО=ОВ=АО=ОВ


 А=
А= В=
В= С=
С=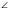 D = 900
D = 900
D С 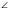 OAD=
OAD=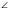 AOB=
AOB=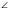 BOC=
BOC=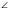 COD = 450
COD = 450
Прямоугольник и его свойства.
Прямоугольник - это параллелограмм, у которого все углы прямые (900).




 А В Свойства прямоугольника:
А В Свойства прямоугольника:
1) Диагонали прямоугольника пересекаются и

 точкой пересечения делятся пополам
точкой пересечения делятся пополам
С D 2) Противоположные стороны прямоугольника
попарно равны.
Прямоугольный треугольник.
Прямоугольный треугольник – это треугольник, у которого один из углов прямой (900).
Две прилежащих стороны к прямому углу называются катетами, сторона, которая находится напротив прямого угла – гипотенуза.
АС, СВ – катеты, АВ – гипотенуза, 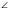 С = 900
С = 900
 А Гипотенуза больше катета.
А Гипотенуза больше катета.
Сумма острых углов прямоугольного треугольника равна 900.
Катет прямоугольного треугольника, лежащего против угла в
300, равен половине гипотенузы.
 В прямоугольном треугольнике квадрат гипотенузы равен
В прямоугольном треугольнике квадрат гипотенузы равен
С В сумме квадратов катетов AB2 = AC2 + BC2
Геометрия на клетчатой бумаге
Узлами сетки называются точки пересечения её вертикальных и горизонтальных линий. Площадь одной клетки считается равной 1.
Определение. Треугольник, вершины которого являются узлами сетки, называется простейшим,
если ни внутри него, ни на его сторонах нет узлов сетки, кроме его вершин.
Лемма 1. Площадь любого простейшего треугольника равна ½.
Лемма 2. Любой треугольник с вершинами в узлах сетки можно разбить на простейшие.
Лемма 3. Любой многоугольник можно разбить на треугольники, вершины которых являются вершинами исходного многоугольника.
Следствие. Любой многоугольник с вершинами в узлах сетки можно разбить на простейшие треугольники.
Факт. Сумма углов n-угольника равна (n − 2)180°.
Пусть дан многоугольник с вершинами в узлах сетки. Обозначим через В – число узлов сетки внутри многоугольника, а через Г — на границе.
Лемма 4. В разбиении многоугольника на простейшие треугольники равно 2В + Г − 2 треугольников.
Лемма (правило параллелограмма). Если три вершины параллелограмма являются узлами сетки, то такова же и четвёртая вершина.
Теорема. Если n ≠ 4, то не существует правильного n-угольника с вершинами в узлах сетки.
Классификация задач из КИМов ОГЭ
Задачи распределила несколько типов это:
1) определение градусной меры угла;
2) определение тангенса угла (косинуса, синуса);
3) определение площади той или иной фигуры – трапеции, параллелограмма, сектора круга, треугольника и т.п.;
4) определение наибольшей (наименьшей) медианы (высоты) треугольника;
5) определение радиуса вписанной в треугольник (описанной около треугольника) окружности;
6) определение площади сложных или составных фигур.
Как найти градусную величину угла, изображенного на клетчатой бумаге.
Среди типовых заданий на данную тему, попадаются как совсем легкие, так и задания, которые ставят, прямо скажем в тупик. Как же их решать? Предлагаю свой очень легкий способ решения. Такие задания делятся на два типа.
Найти градусную величину угла, изображенного на клетчатой бумаге
Найти градусную величину угла, вписанного в окружность.
Определение тангенса угла (косинуса, синуса);
Для решения задач нужно помнить, как строятся углы 900 , 450,300 .
Рассмотрим те задания, где нужно найти градусную величину угла, не вписанного в окружность, а просто изображенного на клетчатой бумаге.


Данный угол – тупой, и можно заметить, что левый луч, образующий его, является биссектрисой прямого угла (см. второй рисунок). Тогда градусная мера этого угла равна: 1350
В интернете очень много способов развернутого решения таких заданий, через цепочку продолжительного решения. Оно конечно правильно, но получается большое решение. Экзамен требует мобилизации умственных усилий. Поэтому предлагаю быстрое интуитивное решение на основе логического мышления.
Очень легкий геометрический способ с помощью "Поворота"
Короткое и очень быстрое решение, может быть "ручным" способом, но тем не менее правильное. Для начала решим совсем легкие задания.
Для того, чтобы решить такие задания достаточно запомнить градусную величину всего лишь двух углов, изображенных на клетчатой бумаге.
Это углы 90° и 45° (по диагонали клетки). Такие углы будем называть " стандартными".
Вычислим градусную меру таких углов.
Задача 1 На клетчатой бумаге изображен угол. Найдите его градусную величину.

Задача 2. На клетчатой бумаге изображен угол. Найдите его градусную величину.

Воспользуемся геометрическим преобразованием "Поворот". Что такое поворот?
Поворот является движением, поскольку представляет собой отображение плоскости на себя, при котором сохраняются расстояния.
Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном направлении. Угол, на который поворачивается фигура, относительно точки, называется углом поворота.
Например, если заданный угол на клетчатой бумаге рассматривать как угол, образованный между минутной и часовой стрелками часов, необходимо просто передвинуть стрелки на один и тот же угол. Поворот можно осуществить как по часовой стрелке, так и против часовой.
Задача 3. На клетчатой бумаге изображен угол. Найдите его градусную величину.

Описание решения. Повернем угол по часовой стрелке. Получим новое положение данного угла для визуального определения градусной его меры. Из рисунка видно угол равен 90°.

Описание решения. Повернем угол по часовой стрелке. Получим новое положение данного угла для визуального определения градусной его меры. Из рисунка видно угол равен 45°.
Определение синусов, косинусов, тангенсов углов.
Здесь придется вспомнить геометрические определения синуса, косинуса, тангенса:
Синус угла – отношение противолежащего катета к гипотенузе.
Косинус угла – отношение прилежащего катета к гипотенузе.
Тангенс угла – отношение противолежащего катета к прилежащему.
Задача 4. Определить синус, косинус и тангенс угла.

Для того, чтобы воспользоваться определениями синуса, косинуса и тангенса, надо сначала выделить прямоугольный треугольник.
Конечно, удобнее вычислять, если катеты и гипотенуза этого треугольника будут целыми числами. Катеты, понятно, лежат на прямых, образующих саму решетку, поэтому нужно смотреть на луч этого угла, который станет гипотенузой нашего треугольника, и найти такое место, где этот луч пересечет узел решетки:


Тогда в нашем треугольнике катеты – 3 и 4 клетки, а гипотенузу найдем по теореме Пифагора с2 = 42 + 32, с2 =16 + 9 = 25, с = 5.
Тогда: синус угла – 4/5, или 0,8, косинус угла – 3/5, или 0,6, тангенс угла – 4/3, или 1,33.
Задача 5. Определить тангенс угла:
Вспомним, что тангенс тупого угла равен тангенсу острого, смежного с ним, взятого с отрицательным знаком.


Надо найти тангенс смежного острого угла. Так как луч, образующий его – гипотенуза прямого угла и проходит прямо по узлам решетки, то катеты треугольников, образуемых этим лучом, всегда равны. Тогда тангенс равен:
Ответ: -1
Задача 6. Определить тангенс угла.
Данный угол – острый, его тангенс – положительный. Осталось найти подходящий узел решетки, чтобы построить прямоугольный треугольник (для этого черным помечена опорная точка – узел решетки). В этом треугольнике считаем количество клеточек в каждом из катетов и определяем тангенс. У нас катеты – 1 и 4 клеточки, искомый тангенс – .
Задача 7. Определить тангенс угла.

Данный угол – тупой, значит, его тангенс – отрицателен. Определяем тангенс смежного с ним острого угла, ставим перед ним минус. Чтобы определить тангенс острого угла, выбираем целый узел, через который проходит луч, образующий угол – помечен черной точкой. Катеты получившегося треугольника – 1 и 3 клетки, тангенс равен отношению противолежащего катета к прилежащему, значит, тупого угла – (-3).
Нахождение расстояния от точки А до прямой a.
1. Построим прямоугольник АВСD так, чтобы точка С принадлежала прямой а, и прямоугольник СКМО, так чтобы точка С была общей вершиной для этих прямоугольников.
2. СМ – диагональ прямоугольника СКМО. Проведем диагонали АС прямоугольника АВСD. Угол АВМ = 900, так как треугольник ВОМ равен треугольнику СВА и треугольники СКМ и СDА равны, значит АС перпендикулярен СМ, т. е. АС перпендикулярен а. АС - расстояние от точки А до прямой а.
3. Найдем АС по теореме Пифагора АС2=АD2+DС2 АС=√22+12=√5, АС=√5.
При нахождении расстояния от точки до прямой важно помнить следующее:
Заключение.
Задачи на клетчатой бумаге – хорошая альтернатива обычным задачам по геометрии. Ясная формулировка, готовый рисунок – все это помогает ученику правильно рассмотреть задачу и сконцентрироваться на ее точном решении.
Я считаю, что изученная мною новая тема, будет интересна многим и сможет привлечь остальных учащихся к разным видам решению задач.
Изучая эту тему, я подготовилась к решению экзаменационных задач на ОГЭ, я надеюсь, что такие задачи приобретут большую распространенность среди учащихся 9-11 классов.
При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать как они могут помочь. По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты, связанные с прямоугольным треугольником. Решение таких задач не предполагает использование циркуля и линейки, а осуществляется непосредственно на рисунке клетчатой бумаги.
При подготовке данного проекта я посетила различные сайты по данной теме, изучала различную литературу, решала задачи. В итоге расширила свои знания в этой области, узнала много нового и интересного. Оказалось, что задач, построений, игр связанных с клеткой очень, очень много.
Я поняла, что наличие под рукой тетради в клетку удобно для решения подобных задач. Во многих задачах такого типа нужна смекалка, воображение и логика. Исследования дали способы приближенного построения углов по клеткам. Для практического применения удобнее пользоваться способом 4х4, потому что легче запомнить и оперировать. Для построения же углов с меньшей погрешностью эффективнее использовать способ 6х6.
Всё это говорит о том, что геометрические задачи на клетчатой бумаге достойны отдельного разговора.
Литература
1) Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, учебник - 7-9 класс. -М.: Просвещение, 2014,
2) ru-wiki.ru/wiki/Геометрия
3) ege.sdamgia.ru/test?theme=252
4) И.Смирнова, В.Смирнов «Геометрия на клетчатой бумаге».Чистые пруды. Москва – 2009 г.
4












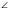 А=
А=


 А В Свойства прямоугольника:
А В Свойства прямоугольника: А Гипотенуза больше катета.
А Гипотенуза больше катета. В прямоугольном треугольнике квадрат гипотенузы равен
В прямоугольном треугольнике квадрат гипотенузы равен 









