Муниципальное бюджетное общеобразовательное учреждение
«Хвощевская школа»
Конкурс исследовательских работ по математике
«Математика и красота»
для учащихся 7-11 классов
Номинация: Математика и искусство
Исследовательская работа
«Вклад П.Л.Чебышева в конструировании одежды»
Подготовила:
Фролова Надежда
9 класс
Руководитель:
Колесова Ольга Викторовна
учитель математики
2015г.
Содержание
Введение…………………………………………………………….……………3
Результаты анкетирования…………………………………………………..3
Типология женских фигур…………………………………………………...5
Развитие женского костюма……………………………………………...….6
Приближенные методы конструирования одежды………………………...7
Метод расчета разверток деталей одежды по образцам моделей………...7
Заключение……………………………………………………………………..11
Список Интернет-ресурсов…………………………………………………….12
Введение
Произведение искусств это некая материальная конструкция, т.е. как предмет, имеющий характеристику. Одновременно это чувственно воспринимаемый облик. Искусство делится на три класса: пространственные, временные и пространственно-временные. Различают изобразительный и не изобразительный виды искусств. Пространственное искусство- живопись, скульптура, фотоискусство, графика изобразительное искусство. Временное искусство- литература (изобразительное), музыка. Пространственно временное: актёрское и танцевальное искусство.
Актуальность. Костюм находится во взаимосвязи с предметным окружением и с человеком, его обладателем, и с обществом, являясь продуктом его культурных и социально-экономических возможностей. Воплощение идеального образа в костюме проходит в сфере прикладного искусства (создание уникальных образцов). Создание массового костюма происходит в сфере промышленного производства и требует серьёзной дизайнерской обработки, образца, на стадии проектирования учитывается основные факторы формы образца костюма.
Технические- выбор материала конструкций, технологического цикла, позволяет дизайнеру (художнику конструктору очертить основу- общий вид), будущие формы изделия. Далее гармонизация формы средствами композиции (от целого к отдельным элементам).
Цель исследовательской работы:
применение математических расчетов в создание моделей одежды.
Задачи:
1.Провести обзор Интернет ресурсов по теме.
2. Показать практическое применение математических расчетов в искусстве моделирования.
3. Изучить вклад Чебышева П.Л. в конструирование одежды.
4. Познакомить учащихся школы с автобиографией математика 19 века П.Л.Чебышева.
Методы исследовательской работы: Сбор и структурирование собранного материала на различных этапах исследования. Выполнение рисунков, чертежей, фотографий. Предполагаемое практическое применение: Возможность применения полученных знаний в повседневной жизни, при изучении тем на других предметах. Знакомство и обработка литературных материалов, данных из Интернета.
1. Результаты анкетирования
Я провела анкетирование среди учениц 7-11 классов по следующим вопросам:
1.Какое из искусств относится к прикладному:
а)музыка б)живопись в)поэзия г)моделирование
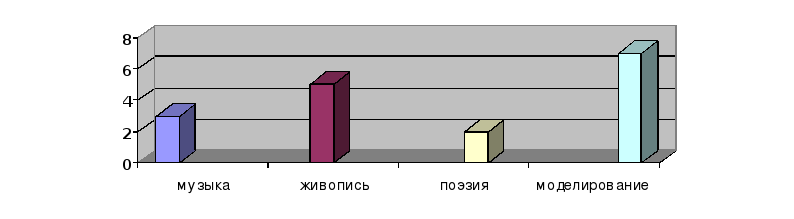
2.С каким из перечисленных искусств математика связанна в высшей степени?
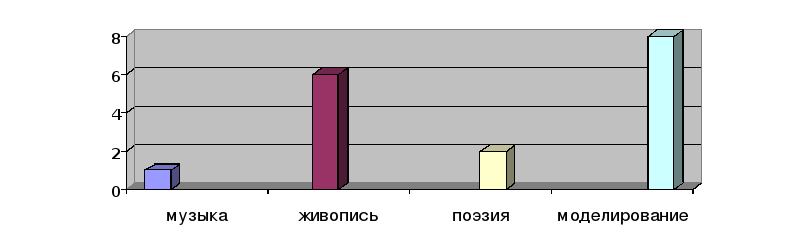
3.Какая часть женского платья наиболее сложна для пошива
а)Рукав б)лиф в)юбка?
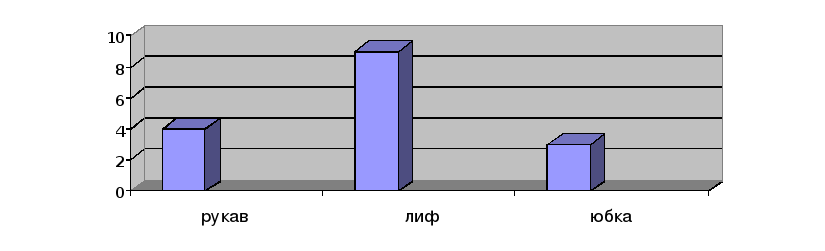
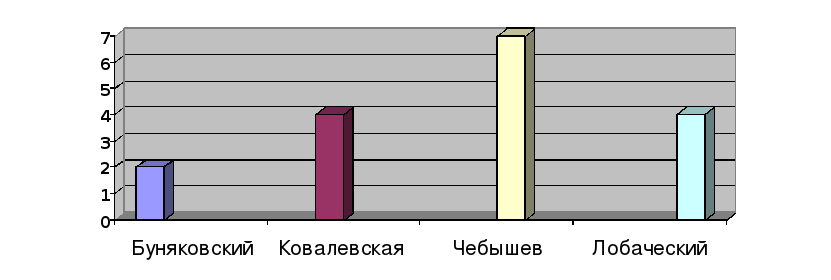
4. Знайте ли вы кто из выдающих математиков 19 века написал работу «О кройке одежды» ? :
а)Буняковский В.Я. в)Чебышев П.Л.
б)Ковалевская С.В. г) Лобачевский Н.И.
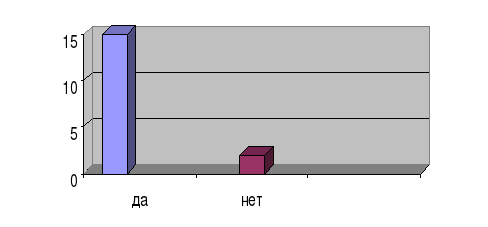
5.Хотели бы вы узнать об этой работе по подробнее :
а)да б)нет
2. Типология женских фигур
Начальные этапы конструирования связаны с появлением кроеной одежды. Кроить (франц. tailler) — в переводе дословно означает делать по росту, по мерке.
Все фигуры делятся на пять основных типов
1) Х-фигура или «песочные часы», – это пропорциональная фигура, ширина плеч соответствует ширине бедер с ярко выраженной талией;
2) Н-фигура или «прямоугольник», бедра и плечи сбалансированы, а талия не явно выражена;
3) А-фигура или «треугольник», – бедра шире плеч и талия явно выражена;
4) V-фигура или перевернутый «треугольник», – плечи шире бедер и талия не явно выражена;
5) О-фигура или «круг» – плечи и бедра сбалансированы, в области талии значительный объем.
| Тип фигуры «Х»
Добавить в избранное" name="Picture 4"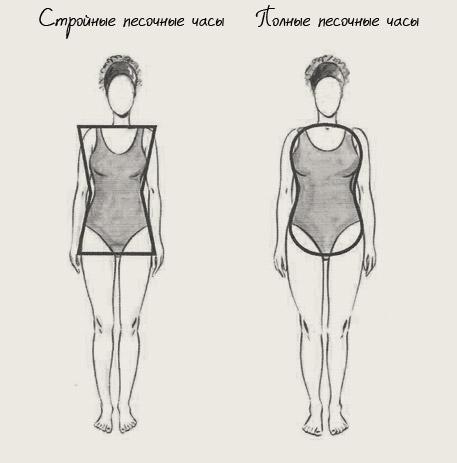 | Тип фигуры «прямоугольник 
| Тип фигуры «А» 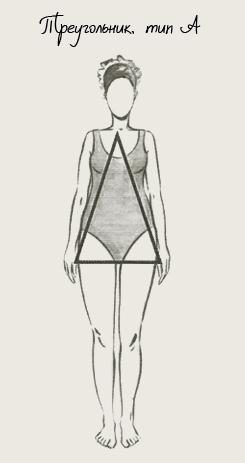
|
| Тип фигуры «треугольник» 
| Тип фигуры «V» 
| Рекомендации по выбору одежды для каждого типа фигуры смотри в приложении 1.  |
3. Развитие женского костюма
Историю совершенствования формы и конструкции одежды можно условно разделить на два направления: первое — эволюционный рост вместе с развитием самого человека и общества,

и второе направление — развитие формы и конструкции одежды под влиянием моды. В процессе развития одежды происходит накопление опыта, типизация покроев, закрепление отдельных элементов ее конструкции и видоизменения одежды в соответствии с изменяющимися условиями жизни: материально-технической базы и общей культуры.
Основной задачей конструирования одежды является разработка чертежей деталей для индивидуальной или типовой фигуры. Каждая методика конструирования включает в себя информацию о фигуре человека или готовом изделии, методы обработки полученной информации в виде технических расчетов и формул, с помощью которых устанавливаются размеры конструктивных отрезков и узлов деталей одежды, и способы геометрического построения и членения конструкции одежды. При конструировании учитываются особенности телосложения, покрой и способы технологической обработки, то есть то, что в конечном итоге формирует постоянную систему внутренней информации, присущую каждой методике.
Существующие методы конструирования по точности и обоснованности получаемых результатов можно разделить на приближенные и инженерные (необходимо понимать, что их точность не может быть выше точности исходных измерений. Следовательно, чем больше у конструктора имеется информации о фигуре человека, тем больше шансов построить что-то достойное внимания). К приближенным методам построения относятся муляжный, расчетно-графический и геометрический методы. Методы триангуляции, секущих плоскостей, конструктивных полос и поясов и геодезических линий — это инженерные методы конструирования одежды.
4. Приближенные методы конструирования одежды
Муляжный метод
Муляжный метод появился много веков назад и до сих пор не утратил своей актуальности.
Расчетно-графические методы
Формирование расчетно-графических методов конструирования одежды началось в конце 18 — начале 19 вв. Высококвалифицированные закройщики, обобщив свой опыт многократно повторяющейся работы, стали применять несложные эмпирические расчеты и графические построения для предварительной разработки чертежей кроя. Известно несколько десятков разновидностей расчетно-графических методов.
Пропорционально-расчетный метод имел много разновидностей и как бы развивал предшествующие системы кроя. Совершенствование шло в направлении изучения и учета строения тела человека, нахождении более правильного членения деталей и узлов изделия, введение новых дополнительных проекционных измерений.
Геометрический метод
Его еще называют «вторая кожа». Имеется в виду, что в качестве основы используют развертку поверхности фигуры или манекена с последующим конструктивным построением разверток основных деталей одежды.
Метод триангуляции
Общим приемом построения приближенной технической развертки состоит в том, что заданную поверхность разбивают на отдельные элементы и заменяют их элементами условно развертывающихся поверхностей, которые затем развертывают. Точность аппроксимации зависит от количества числа элементов, разбивающих кривую поверхность.
Метод секущих плоскостей
Метод является одной из первых попыток получить развертку деталей одежды способами начертательной геометрии и черчения.
Метод геодезических линий
Сущность метода заключается в моделировании на поверхности ряда геодезических линий с заданным шагом и последовательным построением разверток выделенных участков поверхности, ограниченных геодезическими линиями, на плоскости. Метод позволяет получить развертку поверхности детали, по которой можно определить величины необходимой технологической обработки: размеры вытачек, величину посадки или растяжения ткани. Этот способ в дальнейшем нашел свое применение при сканировании, получении информации о фигуре.
Подробнее о выше перечисленных методах смотри в приложении 2
5. Метод расчета разверток деталей одежды по образцам моделей
Основой метода служат идеи академика П.Л.Чебышева о природе изменения структуры тканей при одевании поверхности.
В одежде, изготовленной из клетчатой ткани с некрупной клеткой, легко заметить, что прямоугольные клетки изменяются на кривых участках поверхности тела в параллелограммы. На эту особенность одевания поверхности тканью впервые обратил внимание академик П.Л. Чебышев, который в своей работе “О кройке одежды” еще в прошлом веке математически доказал возможность расчета разверток плотнооблегающих оболочек из ткани для различных поверхностей.
одежде, изготовленной из клетчатой ткани с некрупной клеткой, легко заметить, что прямоугольные клетки изменяются на кривых участках поверхности тела в параллелограммы. На эту особенность одевания поверхности тканью впервые обратил внимание академик П.Л. Чебышев, который в своей работе “О кройке одежды” еще в прошлом веке математически доказал возможность расчета разверток плотнооблегающих оболочек из ткани для различных поверхностей.
Рассказывают, что однажды П.Л. Чебышев ехал на пролетке и обратил внимание на обтянутую тканью спину извозчика. Через некоторое время он сделал в Париже доклад “О кройке одежды”, в котором заложил основы теории сетей.
П.Л. Чебышев как математик разработал метод развертывания сложных поверхностей с использованием сетей. Метод чебышевских сетей широко применяется в технике. С помощью этого метода проектируют сложные тентовые покрытия при строительстве зданий и сооружений из железобетона, каркасы судов, рассчитывают конструкции парашютов и т.д.
Чебышевская сеть состоит из двух семейств линий, которые при пересечении образуют четырехугольники или параллелограммы с равными противоположными сторонами. Эта сеть может быть образована на любой поверхности, с ее помощью можно исследовать поверхности и аналитически рассчитывать их развертки.
Ткань имеет сетчатое строение. Чебышев увидел в ткани способность в определенных условиях становиться сетью поверхности. В своих научных трудах он подробно рассмотрел эти условия с целью использования сетчатой структуры для построения разверток деталей одежды.
Действительно, при рассмотрении ткани видно, что на плоскости ее нити образуют сеть прямоугольников с равными параллельными сторонами (рис. 1.1).
Если к ткани приложить небольшие растягивающие усилия, направленные под углом к нитям, ее элементарные прямоугольники преобразуются в параллелограммы.
Величина прилагаемых растягивающих усилий должна быть такой, чтобы длина нитей не изменялась. При приложении небольших растягивающих усилий под углом к нитям ткань из плоского состояния переходит в объемное, и если ее разместить на участке поверхности, она может стать оболочкой поверхности.
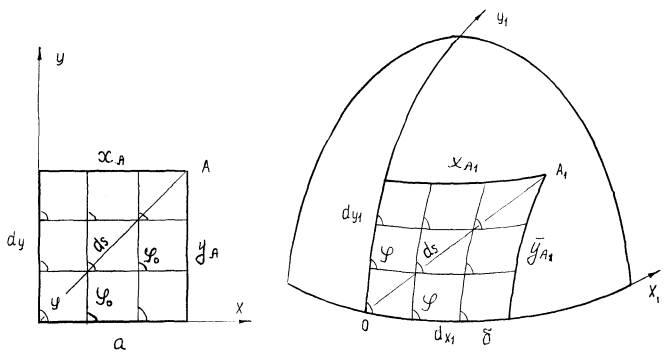
Рис. 1.1. Схема состояния чебышевской сети из ткани на плоскости и на поверхности шара.
Под оболочкой поверхности принято понимать покрытие какой-либо поверхности, толщина которого несравненно мала по отношению к покрываемой площади, при обязательном условии плотного прилегания. При плотном прилегании каждой точке в оболочке соответствует только одна точка на поверхности. В оболочке не может быть разрывов и складок.
Чтобы ткань перевести в состояние оболочки, к ней необходимо приложить небольшие растягивающие усилия. Ткань оказывает заметное сопротивление растягивающим усилиям только в том случае, если эти усилия направлены вдоль нитей. Приложение таких усилий под углом к нитям вызывает изменение сетевых углов j, то есть преобразование элементарных прямоугольников, образованных нитями ткани, в параллелограммы.
Сетевыми углами принято называть углы в элементарных ячейках чебышевской сети. Для ткани это углы, образованные нитями основы и утка и однонаправленные с осями координат. При этом условии нити ткани на поверхности образуют сеть из параллелограммов, а сама ткань может быть приравнена к чебышевской сети.
Оболочка из ткани на поверхности должна быть строго координирована и находиться в равновесном состоянии. Если к одиночной нити на поверхности приложить небольшое растягивающее усилие, то она приобретет равновесное состояние только в том случае, если расположится по геодезической линии поверхности – S (рис. 1.1).
Геодезическая линия, или, как ее определил П.Л. Чебышев, линия наикратчайших расстояний, есть наименьшее расстояние между двумя точками на поверхности. Геодезическая линия обладает свойством развертываться на плоскости в прямую при сохранении своей длины. Ортогональные геодезические линии развертываются на плоскости в ортогональные прямые.
Если к ткани прилагать небольшие растягивающие усилия, то в оболочке определенного участка поверхности только одна нить основы и только одна нить утка будут совпадать с направлением геодезической линии поверхности. Это объясняется тем, что в оболочке неразвертываемой поверхности нити ткани, изгибаясь, остаются равноудаленными друг от друга и параллельными, а геодезические линии не могут быть параллельны между собой, что обусловлено особенностью неразвертываемых поверхностей. Например, для сферической поверхности геодезическими линиями являются меридианы, но для такой поверхности они не могут быть параллельными между собой.
В оболочке заданного участка поверхности можно выбрать только одну пару нитей ткани, положение которых будет совпадать с направлением ортогональных геодезических линий. Эту пару нитей принимают за оси координат – исходные линии развертывания. В развертке это ортогональные прямые.
Таким образом, основные положения чебышевских сетей при переходе ткани из плоского состояния в объемное можно сформулировать следующим образом:
–длина нити ткани не изменяется, происходит лишь ее изгибание и изменение сетевого угла. При этом стороны элементарных участков остаются параллельными;
–для того чтобы ткань из плоского состояния перешла в оболочку поверхности, необходимо к ней приложить усилие. В качестве таких усилий могут быть вес ткани, трение, закрепление зауженных изделий швами и др.;
–ткань оказывает сопротивление прилагаемым усилиям только в том случае, если эти усилия направлены вдоль нити, а если по диагонали – то не оказывает;
–ткань на поверхности будет находиться в равновесии, если нити, к которым приложены необходимые усилия, располагаются на поверхности по геодезическим линиям;
–в каждой части поверхности может быть выбрана только одна пара ортогональных нитей, положение которых совпадает с геодезическими линиями.
Решением задачи об одевании поверхностей тканью после Чебышева занимались и другие математики. Однако результаты их исследований не могут быть непосредственно использованы при конструировании одежды вследствие того, что они решали вопросы дифференциальной геометрии, в задачу которой не входит изучение методов определения оболочек из ткани. Вместе с этим их исследования показывают, что строгое решение задачи об одевании поверхностей приводит к значительным математическим осложнениям. Поэтому решать эту задачу для расчета разверток оболочек из тканей надо приближенными методами.
Заключение
Взаимопроникновение геометрии и моделирования — один из механизмов интеллектуального развития человека и его творческих способностей, что подтверждается многочисленными примерами. Произведения искусства разных периодов служили источником вдохновения для создания модных стилей в одежде, аксессуарах, прическе. Интересно, что современные учебники типа “Основы конструирования одежды” содержат десятки страниц, посвященных изложению методов проектирования разверток одежды в «чебышевских сетях», а великие кутюрье современности Валентин Юдашкин, Вячеслав Зайцев, Ив Сен Лоран либо Пьер Карден вряд ли догадываются, кому из гениальных ученых они обязаны частью своего успеха.


Валентин Юдашкин


Вячеслав Зайцев
Мы не осознаем, насколько наша жизнь связана с математикой. Даже такие творческие направления деятельности человека, как музыка, живопись, моделирование без математических законов не могут существовать и развиваться. В своей работе я постаралась это показать. В моей работе можно получить ответы на различные вопросы. Работа продемонстрирует на примерах ошибочность мнения о скучности математики.
Список Интернет-ресурсов
http://shei-sama.ru/publ/osnovy_konstruirovanija_odezhdy/25_raschjot_razvjortok_obolochek_iz_tkani/47-1-0-644
http://www.openclass.ru/user/514786
http://gim13.tomsk.ru/files/img/issledovatelskaja%20rabota%20Plotnikova.pdf
http://nashaucheba.ru/v12053/%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B8_%D0%BF%D0%BE_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%BC%D1%83_%D1%80%D0%B0%D1%81%D1%87%D1%82%D1%83_%D0%BE%D0%B1%D0%BE%D0%BB%D0%BE%D1%87%D0%B5%D0%BA
http://fashion-school.narod.ru/alman1.htm
- http://uisrussia.msu.ru/docs/nov/2012/118/nov_2012_118_25.htm
- http://www.pereplet.ru/nauka/Soros/pdf/9807_122.pdf
12


















 одежде, изготовленной из клетчатой ткани с некрупной клеткой, легко заметить, что прямоугольные клетки изменяются на кривых участках поверхности тела в параллелограммы. На эту особенность одевания поверхности тканью впервые обратил внимание академик П.Л. Чебышев, который в своей работе “О кройке одежды” еще в прошлом веке математически доказал возможность расчета разверток плотнооблегающих оболочек из ткани для различных поверхностей.
одежде, изготовленной из клетчатой ткани с некрупной клеткой, легко заметить, что прямоугольные клетки изменяются на кривых участках поверхности тела в параллелограммы. На эту особенность одевания поверхности тканью впервые обратил внимание академик П.Л. Чебышев, который в своей работе “О кройке одежды” еще в прошлом веке математически доказал возможность расчета разверток плотнооблегающих оболочек из ткани для различных поверхностей.














