МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ШКОЛА №16»
ИТОГОВЫЙ ИНДИВИДУАЛЬНЫЙ
УЧЕБНЫЙ ПРОЕКТ
Тема:
«Представление чисел с помощью систем счисления»
Выполнила: ученика 9 В класса,
Еркина Н.А.
Руководитель проекта: учитель информатики, Галкина И. В.,
_________________________
(подпись)
«_____» __________________2022г
г. Саров, 2022
СОДЕРЖАНИЕ
ВВЕДЕНИЕ…………………………………………………………………………………………….3
1 ЧИСЛО 5
1.1 Понятие числа 5
Понятие системы счисления 5
Понятие алфавита 5
1.2 Возникновение и развитие систем счисления 5
2 АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 11
2.1 Сложение 11
2.2 Вычитание 11
2.3 Умножение 11
2.4 Деление 12
ЗАКЛЮЧЕНИЕ 13
ЗАКЛЮЧЕНИЕ 14
СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ-ИСТОЧНИКОВ 15
ВВЕДЕНИЕ
Изучение этой темы связана с тем фактом, что в повседневной жизни мы используем числа, которые являются объектами различных систем счисления. Они используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений младшего школьника, выполняемых карандашом на бумаге, кончая вычислениями, выполняемыми на суперкомпьютерах.
Например, вы задумывались, почему люди используют именно десятичную систему счисления для записи чисел?
На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног. По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки.
Актуальность:
Эта тема не перестанет быть актуальна независимо от времени, потому что каждый день мы пользуемся счетом, о происхождении которого даже многого не знаем. На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов, а всякая совокупность, содержащая большее число предметов, объединялась в понятии "много". Наши пословицы сохранили память об этой эпохе ("Семь раз отмерь – один раз отрежь", "У семи нянек дитя без глазу", "Семь бед дин ответ" и т. д.). В русском языке слово "сороконожка" имеет смысл "многоножка"; выражение "сорок сороков" означало в старину число, превосходящее всякое воображение. В наши дни, когда мы и не думаем о возникновении счета, в век высоких технологий, значение данной работы трудно переоценить.
Очевидно, что современный человек каждый день запоминает номера машин и телефонов, в магазине подсчитывает стоимость покупок и т.д. Числа, цифры … они с нами везде. Числа складываются из цифр по особым правилам. на разных этапах развития человечества, у разных народов эти правила были различны и сегодня мы их называем системами счисления.
Цель:
Узнать, почему десятичная система счисления является наиболее удобной.
Для достижения цели необходимо решение следующих задач:
1. Познакомиться с возникновением и развитием систем счисления.
2. Дать общее представление о роли и назначении систем счисления.
3. Показать, что десятичная система счисления самая удобная в информатике.
4. Составить памятку «Десятичная система счисления».
Методы исследования:
Изучение литературы, интернет ресурсов, методический материал по теме, анализ, сравнение.
ЧИСЛО Понятие числа
Число – это некоторая абстрактная сущность для описания количества.
Понятие «число» является ключевым как для математики, так и для информатики. Люди всегда считали и записывали числа, даже 5 тысяч лет назад. Но записывали их по другим правилам, хотя в любом случае число изображалось с помощью любого или нескольких символов, которые назывались цифрами.
Язык чисел, как и любой другой, имеет свой алфавит. В том языке чисел, которым мы обычно пользуемся, алфавитом служат десять цифр – от 0 до 9. Это десятичная система счисления.
Система счисления – это символический метод записи чисел, представление чисел с помощью письменных знаков.
Алфавит – это способ записи чисел с помощью заданного набора специальных знаков (цифр, букв и т.д.).
1.2 Возникновение и развитие систем счисления
Оказывается, что люди не всегда пользовались привычной нам десятичной системой счисления. Ещё с младшей школы вы знаете, что существуют римские цифры. А в Древнем Вавилоне вообще использовалась шестидесятеричная система счисления.
Без чисел практически невозможно себе представить жизнь современного человека. Благодаря числам мы можем обращаться с деньгами, покупать и продавать товары и услуги. Числа встречаются везде – на футболках спортсменов, часах, калькуляторе, ценниках (рис. 1).

Рис. 1. Ценник
Люди научились считать очень давно, еще в каменном веке. Сначала они просто различали, один предмет перед ними или больше. Через некоторое время появилось слово для обозначения двух предметов. У некоторых племен Австралии и Полинезии до самого последнего времени было только два числительных: «один» и «два». А все числа, большие двух, получали названия в виде сочетаний этих двух числительных. Например, три – это «два, один», четыре – «два, два», пять – «два, два, один».
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Чтобы два человека могли точно сохранить некоторую числовую информацию, они брали деревянную бирку, делали на ней нужное число зарубок, а потом раскалывали бирку пополам (рис. 2).

Рис. 2
Каждый уносил свою половинку и хранил ее. Этот прием позволял избегать «подделки документов». Ведь при возникновении спорной ситуации половинки можно было сложить и сравнить совпадение и число зарубок.
Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, сколько полосок нашито на его рукаве. Этим кодом пользуются малыши, показывая на пальцах свой возраст. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит школьников в мир счета.
Единичная система – не самый удобный способ записи чисел. Записывать таким образом большие количества утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более экономичные системы счисления.
Римские цифры
Мы уже знаем, что в Древнем Риме существовали следующие обозначения:
I=1; V=5; X=10; L=50; C=100; D=500; M=1000.
Обозначения чисел 100, 500 и 1000 пошли от первых букв соответствующих латинских слов (Centum – сто, Demimille – половина тысячи, Mille – тысяча).
Чтобы записать число, римляне использовали не только сложение, но и вычитание ключевых чисел. При этом применялось следующее правило.
Значение каждого меньшего знака, поставленного слева от большего, вычитается из значения большего знака.
Например, запись IX обозначает число 9, а запись XI — число 11. Десятичное число 28 представляется следующим образом:
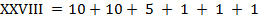 .
.
Десятичное число 99 имеет такое представление: 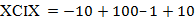 .
.
То, что при записи новых чисел ключевые числа могут не только складываться, но и вычитаться, имеет существенный недостаток: запись римскими цифрами лишает число единственности представления. Действительно, в соответствии с приведенным выше правилом, число 1995 можно записать, например, следующими способами:
МСМХСV = 1000 + (1000 - 100) + (100 -10) + 5, МDССССLХХХХV =1000+500+100+100+100+100+50+10 +10+10+10+5,
МVМ =1000 + (1000 - 5),
МDVD = 1000 + 500 + (500 - 5) и так далее.
Единых правил записи римских чисел до сих пор нет, но существуют предложения о принятии для них международного стандарта.
В наши дни любую из римских цифр предлагается записывать в одном числе не более трех раз подряд. На основании этого построена таблица, которой удобно пользоваться для обозначения чисел римскими цифрами:
| Единицы | Десятки | Сотни | Тысячи |
| 1 I | 10 X | 100 C | 1000 M |
| 2II | 20 XX | 200 CC | 2000 MM |
| 3III | 30 XXX | 300 CCC | 3000 MMM |
| 4IV | 40 XL | 400 CD | |
| 5V | 50 L | 500 D | |
| 6VI | 60 LX | 600 DC | |
| 7VII | 70 LXX | 700 DCC | |
| 8VIII | 80 LXXX | 800 DCCC | |
| 9IX | 90 XC | 900 CM | |
Эта таблица позволяет записать любое целое число от 1 до 3999. Чтобы это сделать, сначала запишите свое число, как обычно (в десятичной системе). Затем для цифр, стоящих в разрядах тысяч, сотен, десятков и единиц, по таблице подберите соответствующие кодовые группы.
Для того чтобы записать числа, большие 3999, применяют специальные правила.
Древнеегипетская система счисления
Примерно в третьем тысячелетии до нашей эры египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и так далее использовались специальные значки – иероглифы.
Все остальные числа составлялись из этих ключевых символов при помощи операции сложения. Например, чтобы изобразить 3252, рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы) (рис. 3).

Рис. 3
Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемешку.
Система счисления называется непозиционной, если в ней количественные значения символов, используемых для записи чисел, не зависят от их положения (места, позиции) в коде числа.
Система счисления Древнего Египта является непозиционной.
Древнеримская система счисления
Примером непозиционной системы счисления, которая сохранилась до наших дней, может служить система счисления, применявшаяся более двух с половиной тысяч лет назад в Древнем Риме.
В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а также специальные знаки для обозначения чисел 50, 100, 500 и 1000 (рис. 4).
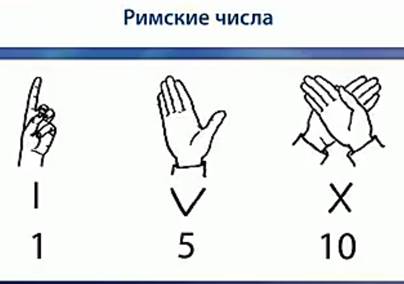
Рис. 4
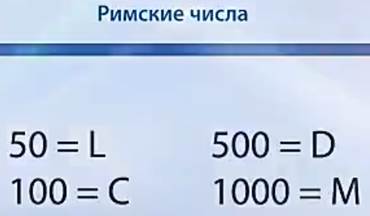
Рис. 5
Обозначения для последних четырех чисел с течением времени претерпели значительные изменения.
Сейчас они записываются так: L, C, D, M (рис. 5).
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать).
Римская система счисления сегодня используется в основном для наименования знаменательных дат, томов, разделов и глав в книгах.
Алфавитная система счисления
Наряду с иероглифическими в древности широко применялись алфавитные системы счисления, в которых числа изображались буквами алфавита. Так, в Древней Греции числа 1, 2, ..., 9 обозначали первыми девятью буквами греческого алфавита. Для обозначения десятков применялись следующие девять букв. Для обозначения сотен использовались последние девять букв.
Алфавитная система счисления существовала и у славян. Только при царствовании Петра I возобладала арабская нумерация (которой мы пользуемся и сейчас).
Позиционные системы счисления
Рассмотренные нами иероглифические и алфавитные системы счисления имели один существенный недостаток – в них было очень трудно выполнять арифметические операции. Этого неудобства нет у позиционных систем.
Система счисления называется позиционной, если количественные значения символов, используемых для записи чисел, зависят от их положения (места, позиции) в коде числа.
Французский математик Пьер Симон Лаплас (1749-1827) такими словами оценил «открытие» позиционной системы счисления: «Мысль – выражать все числа немногими знаками, придавая им значение по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна».
Основные достоинства любой позиционной системы счисления – простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
Сложение

Мы складываем числа уже привычным нам способом, в десятичной системе счисления. Самое главное стоит понять разряды. Вспомните алфавит каждой системы счисления и тогда станет легче.
2.2 Вычитание

Начинаем слева направо, от меньшего разряда к большему. 2 – 1 = 1.
1 – 0 = 1.
3 – 9 = ? Тройка меньше девяти, поэтому позаимствуем единицу из старшего разряда.
13 – 9 = 4.
Из последнего разряда мы взяли единицу для предыдущего действия, поэтому 4 – 1 = 3.
Ответ: 3411.
Умножение
Умножение в любой системе счисления на единицу, всегда даст тоже самое число.

Каждый разряд умножаем на единицу, как обычно справа налево, и получаем число 6748;
6748 умножаем на 8 и получаем число 53984;
Проделываем операцию умножения 6748 на 3. Получаем число 20244;
Складываем все 3 числа, по правилам. Получаем 2570988;
Ответ: 2570988.
Деление
С делением все так же, как и в привычной нам десятичной системе счисления.
ЗАКЛЮЧЕНИЕ
Самыми значимыми для человека среди систем счисления, безусловно, являются двоичная и десятичная системы счисления. Двоичная система счисления используется во всех компьютерных системах. Но десятичная система счисления используется ежедневно для решения математических задач, формирования финансовых результатов, а самое главное это учёт времени, цен в магазине, определенных записей и т.д.
Немаловажной является история развития представлений человека о системы счисления. Сложно представить, что на ранних стадиях развития общества люди не отличали совокупность двух и трех предметов.
Системы счисления прошли сложный путь в своем развитии и сейчас они занимают большую нишу в области информатики. Они являются частью фундаментальной информатики. Существует огромное количество различных систем счисления и для каждой из них можно найти применение в самых различных областях человеческой деятельности. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах. Особое значение на данный момент имеют итерационные системы. В таких системах счисления наиболее важную информацию о числе содержат первые цифры. Это представляет огромный интерес в вопросах сжатия и кодирования информации.
Особая актуальность изучения систем счисления связана с тем, что в будущем вполне может произойти так называемый информационный переворот, связанный с разработкой компьютеров основанных на информационной системах счисления.
В последние годы все основные параметры компьютерной техники ежегодно вырастали в среднем в 4 раза (т.е. в 1000 раз за 5 лет). Ясно, что их экспоненциальный рост не может продолжаться бесконечно (в частности, этому препятствует атомное строение вещества). Как только он прекратится, производители компьютерной техники начнут искать новые пути ее усовершенствования. И тогда они вынуждены будут отказаться от двоичной системы счисления в пользу информационных.
СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ-ИСТОЧНИКОВ
| 1 | Брайан К., Гриффис Т. Алгоритмы для жизни: Простые способы принимать решения – Москва, 2017. С. 7-38 2. |
| 2 | Криницкий Н.А. Алгоритмы вокруг нас. М.: Наука, 2011. [Электронный ресурс]: https://informat.name/articale/art_algmind.html |
| 3 | Деревянченко М. Виды алгоритмов в информатике: примеры. [Электронный ресурс]: https://fb.ru/article/283912/vidyi-algoritmov-v-informatike-primeryi |
| 4 | Босова, Л.Л. «Алгоритмы»: учебник для ВУЗов – 3-е изд. [Текст] / Л.Л. Босова, Ю.Г. Коломенская. – М.: БИНОМ. Лаборатория знаний, 2012. |
| 5 | Кормен, Х. Т. Алгоритмы: вводный курс [Текст] / Кормен Х.Т. – М.: Вильямс, 2014. |
|
| Статья. «Алгоритмическое мышление». [Электронный ресурс]: http://praktiks.com/algoritmicheskoe_myshlenie/ |
| 6 | Кушниренко, А.Г. 12 лекций о том, для чего нужен школьный курс информатики и как его преподавать. [Текст] / А.Г.Кушниренко, Г.В.Лебедев. – Информатика. – 1999. - №1.- С.2-15. [Электронный ресурс]: https://dropdoc.ru/doc/1123530/12-lekcij-o-tom--dlya-chego-nuzhen-shkol._nyj-kurs-informatiki-i |
| 7 | Хеннер, Е.К. Информатика в школе. Нетрадиционные формы обучения: Методические рекомендации. Сб. Вып.1 [Текст] / Е.К. Хеннер, С.В. Русаков, И.Г. Семакин. – Пермь, 2011. |
| 8 | Ершов, А.П. Программирование – вторая грамотность. [Электронный ресурс]: http://ershov.iis.nsk.su/ru/second_literacy/article |
| 9 | Газейкина, А.И. Развитие алгоритмического стиля мышления при обучении студентов ВУЗа. [Электронный ресурс]: https://dspace.susu.ru/xmlui/bitstream/handle/0001.74/5430/4.pdf?sequence=1&isAllowed=y |
| 10 | Соклаков, Е.Н., Алгоритмическое мышление. [Электронный ресурс]: https://informat.name/wp-content/uploads/2016/06/art_algmind.pdf |