| Как не запутаться в многочисленных единицах измерений на уроках математики |
| Методические уловки |
|
Кочева Елена Владимировна Учитель математики ГБОУ СО «Екатеринбургская школа – интернат «Эверест», реализующая адаптированные основные общеобразовательные программы |




Методические уловки при изучении многочисленных единиц измерений.
Как не запутаться в единицах измерений? Для многих учащихся, как начальной школы, так и для учащихся старших классов, тема «Единицы длины, стоимости, площади, объема» является одной из самых запутанных. В этом нет ничего удивительного, так как материал изучается в разное время и зачастую бывает разбросан по нескольким учебникам. Да и взрослому человеку приходится время от времени переводить одни единицы измерения в другие. Если речь идет о единицах длины, то он кое-как справляется с поставленной задачей. А когда требуется перейти от одних единиц площади или объема к другим, то не помогают справочные материалы, опубликованные на обложке тетради.
Известно, что математика один из самых трудных предметов для учащихся с интеллектуальной недостаточностью. Это объясняется, с одной стороны, особенностями усвоения математических знаний учащимися, с другой стороны абстрактностью математических понятий.
В коррекционной школе уже с первого класса учащиеся знакомятся с единицами измерений. И, в дальнейшем, из года в год, они повторяют имеющиеся у них знания и получают новые, вплоть до девятого класса. Но, несмотря на это, к пятому классу большинство детей не имеют необходимых знаний и умений по данной теме или допускают различные ошибки:
(мм, см, дм и м);
трудности при установлении соотношения мер;
при выполнении арифметических действий с числами, полученными при измерении, не принимают во внимание наименования: (7 кг + 30г = 37 кг); переставляют местами разные по величине меры (40 см 3 м); производят неправильную запись наименований, т.е. возможность выразить в более крупной единице (4 км 291 см=42 м 91см)
неточность измерений, неумение выбрать соответствующую единицу измерения, правильно назвать или записать результат измерения простым или составным именованным числом.
Причины перечисленных трудностей и ошибок кроются в особенностях познавательных и психофизических процессов развития учащихся специальной школы.
Но на все перечисленные трудности, нельзя отрицать значимость и необходимость изучения данной темы, которая позволяет тесно связать математические знания с жизнью, учащихся получают практические умения и навыки измерения, необходимые как в повседневной жизни, так и при овладении будущими профессиями.
В данном опыте представлена система работы по изучению единиц измерений стоимости, длины, массы, площади, объема, которая дает возможность показать практическую значимость темы, делает процесс запоминания непринужденным, интересным и прочным, способствует формированию обобщений, развитию целенаправленности действий. Практически все учащиеся хорошо усваивают данную тему.
Важно показать учащимся связь между принятыми единицами длины (стоимости, массы, площади, объема). Для этого можно выстроить единицы измерения «по росту»: от мелкой величины к крупной и, наоборот, от крупной к мелкой. При этом необходимо пояснить, что при замене крупных мер мелкими необходимо умножать и при замене мелких мер крупными - делить (см. рис 1, 2).
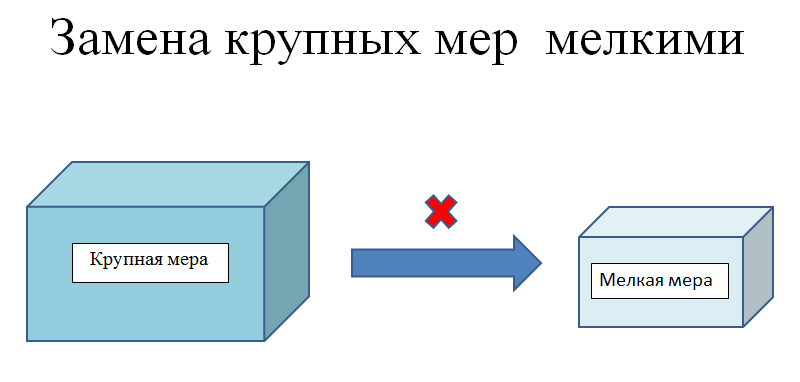
Рис. 1
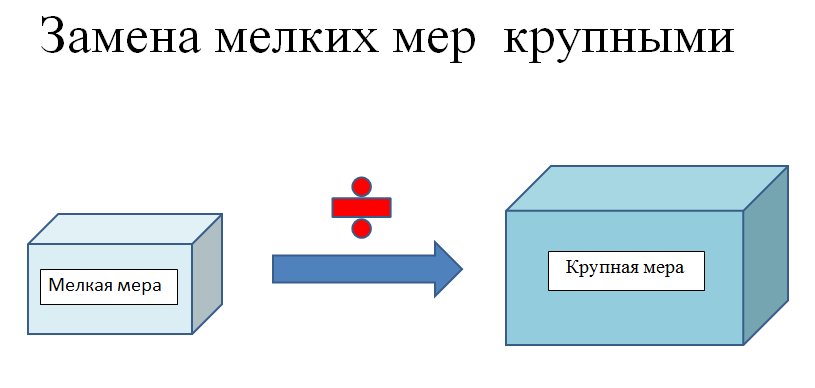
Рис. 2
Говоря о мерах стоимости, объяснять, что при замене рублей на копейки, надо умножать на 100, так как рубли в 100 раз больше копеек, т.к. 1 р. = 100 к. При замене копеек на рубли необходимо делить на 100 (см. рис.3). При записи замен одних мер другими удобно использовать цветные карандаши или цветные ручки.
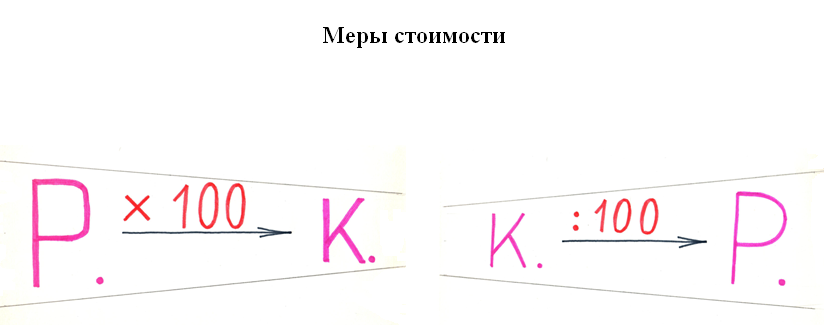
Рис.3
Образец записи:
54 руб. = ( 54 × 100 ) коп. = 5 400 коп.
1 руб. = 100 коп.
6 руб. 83 коп. = ( 6 × 100 + 83 ) коп. = 683 коп.
5 729 коп. = ( 5 729 : 100 ) руб. = 57 руб. 29 коп.
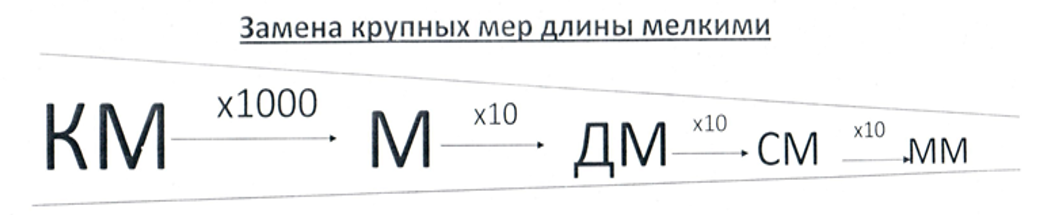
Аналогично объясняем замены и для единиц, длины, массы. Глядя на цепочку, становится понятно: для того чтобы перейти, например, от метров к миллиметрам, необходимо заданное значение длины трижды увеличить в 10 раз, т.е. умножить на 1000, а если надо наоборот, перевести миллиметры в метры, то разделить на 1000 (см. рис. 4, 5, 6). Легко будет ответить на вопрос: какую часть метра составляет 1 миллиметр (тысячную долю). При замене крупных мер мелкими закрепляется правило умножения на 10, 100, 1000: «приписываем» нужное количество нулей, а при замене мелких мер крупными – деление на 10, 100, 1000: « отбрасываем» или получаем деление с остатком.
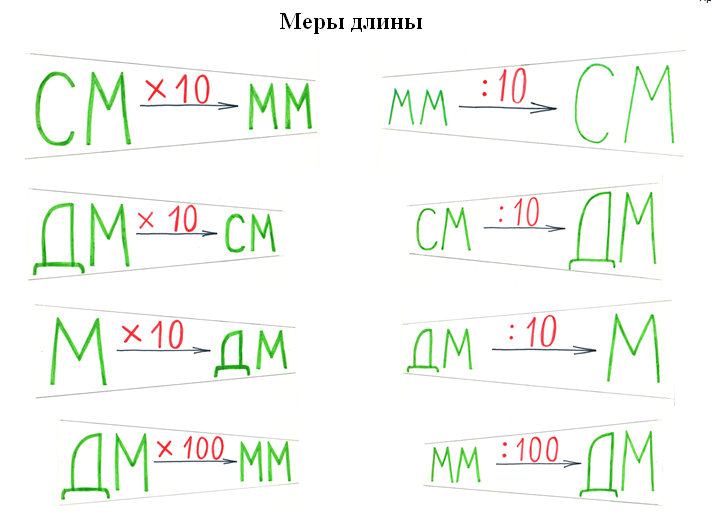
Рис. 4
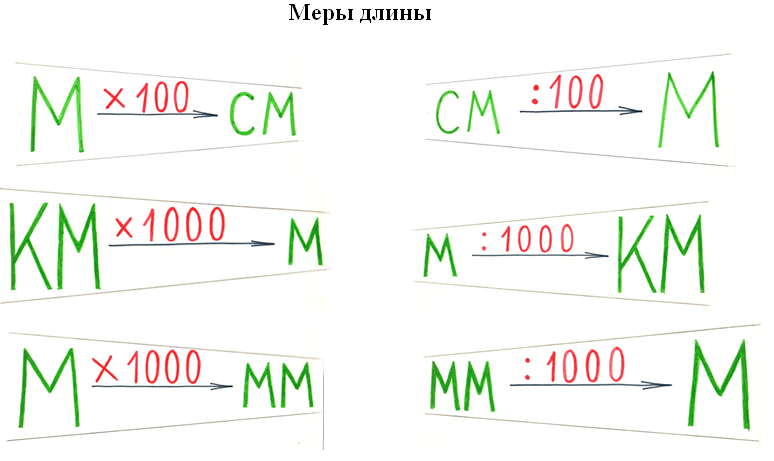
Рис. 5
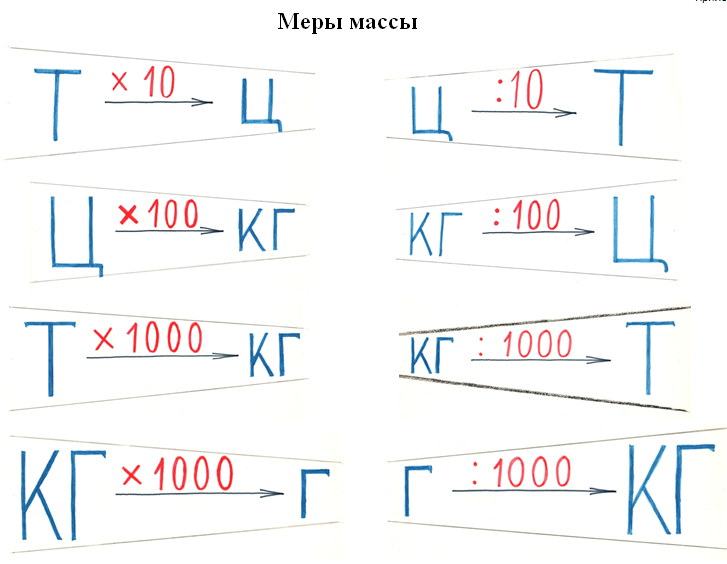
Рис. 6
В качестве обобщающей можно использовать таблицы (см. рис. 7, 8), из которых хорошо просматривается взаимосвязи между единицами длины, массы.
1 см = 10 мм 1 дм = 100 мм 1 м = 1 000 мм
1 дм = 10 см 1 м = 100 см 1 км = 1 000 м
1 м = 10 дм
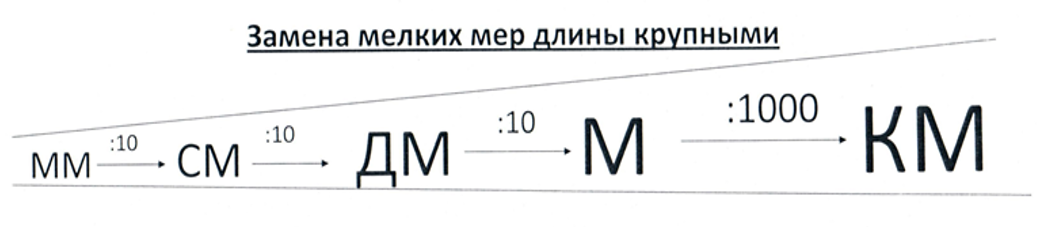
Рис. 7
Образец записи замены мер длины:
2 м = ( 2 × 100 ) см = 200 см
1 м = 100 см
2 м = ( 2 × 10 ) дм = 20 дм
1 м = 10 дм
2 м 45 см = ( 2 × 100 + 45) см = 245 см
1 м = 100 см
2 км 523 м = ( 2 × 1 000 + 523 ) м = 2 523 м
1 км = 1 000 м
367 см = ( 367 : 100 ) м = 3 м 67 см
1 м = 100 см
3 047 м = (3 047 : 1 000) км = 3 км 47 м
1 км = 1 000 м
Образец записи замены мер массы:
4 т = ( 4 × 10 ) ц = 40 ц
1 т = 10 ц
35 ц = ( 35 × 100 ) кг = 3 500 кг
1 ц = 100 кг
3 703 г = ( 3 703 : 1 000 ) кг = 3 кг 703 г
1 кг = 1 000 г
754 кг = ( 754 : 100 ) ц = 7 ц 54 кг
1 ц = 100 кг
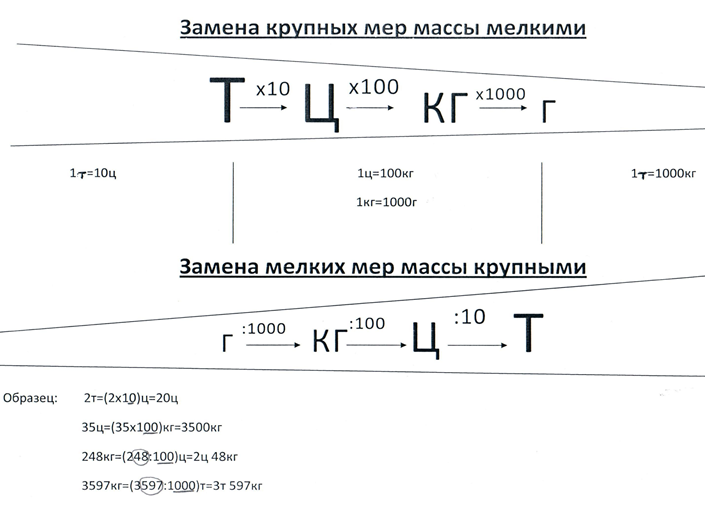
Рис. 8
Отработав, таким образом, переходы от одних единиц к другим, можно приступить к единицам площади, объема. Важно, чтобы учащиеся сами попытались упорядочить их и выстроить похожую цепочку. Для этого можно использовать набор карточек, на каждой из которых записана одна из единиц площади (объема) и предложить учащимся выстроить все единицы «по росту», начиная с самой маленькой и заканчивая самой большой. Аналогичную работу проводим и наоборот: начиная с большой и заканчивая маленькой единицей. Следует задавать учащимся вопросы: чем единицы площади (объема) отличаются от единиц длины?
Каждая единица площади (объема) – квадрат (куб) соответствующей единицы длины, поэтому при переходе от большей единицы площади (объема) к соседней меньшее заданное значение площади (объема) умножаем не на 10, а на 100 = 102 (на 1000 = 103), а при обратно переходе – делим на 100 (1000).
При изучении единиц объема учащиеся могут выстроить нужную цепочку и понять, как осуществляется переход от одних единиц объема к другим.
В качестве обобщающей можно использовать таблицы, из которых хорошо просматривается взаимосвязи между единицами длины, массы, площади, объема (см. рис. 9, 10).
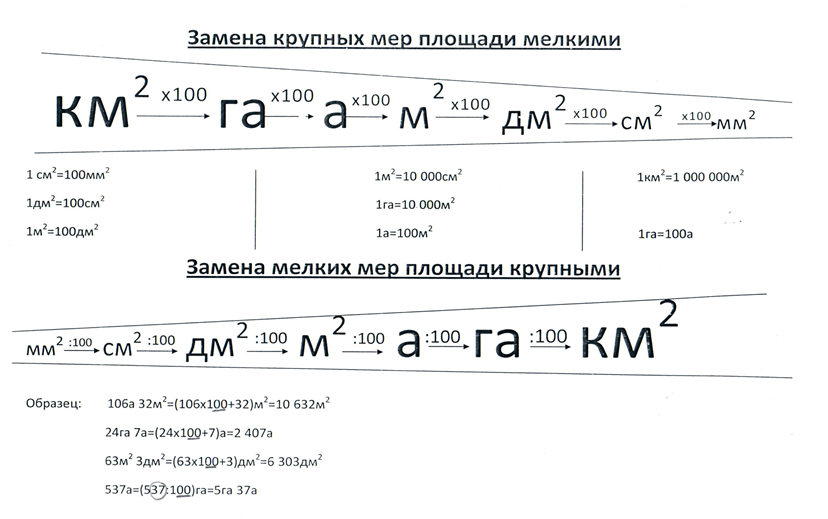
Рис. 9
Образец записи замены мер площади:
24 а = ( 24 ×100 ) м2 = 2 400 м2
1 а = 100 м2
2 га 7 а = ( 2 ×100 + 7 ) а = 207 а
1 га = 100 а
2 890 м2 = ( 2 890 : 100 ) а = 28 а 90 а
1 а = 100 м2
304 602 м2 = ( 304 602 : 10 000) га = 30 га 4602 м2
1 га = 10 000 м2
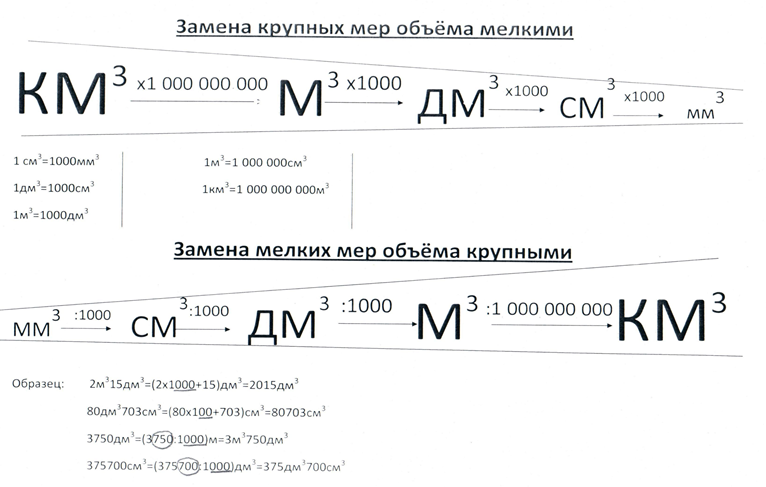
Рис. 10
Когда учащиеся заменяют именованные целые числа десятичными дробями и, заменяя десятичные именованные дроби целыми числами, то в работе предлагаю таблицу, которую учащиеся оформляют в своих тетрадях – памятках.
Рассуждаем следующим образом: 1 р.=100 к. 1 к. – какая доля рубля? (сотая). Сколько цифр после запятой пишем? (две) Сотая доля рубля – копейка. Аналогичным образом рассуждаем и для других мер, составляя таблицу системы мер (десятые, сотые, тысячные доли) (см. рис 11). Проговаривая, что если десятые доли, то пишется одна цифра после запятой, сотые – две цифры после запятой, тысячные – три цифры после запятой.
Образец записи:
6 дм 3 см = 6, 3 дм
118 т 365 кг = 118, 365 т
1 кг 004 г = 1, 004 кг (надо три цифры после запятой, а у нас – одна. Поэтому приписываем перед цифрой 4 два нуля и записываем число десятичной дробью)
806 см = (806 : 100 ) м = 8,06 м
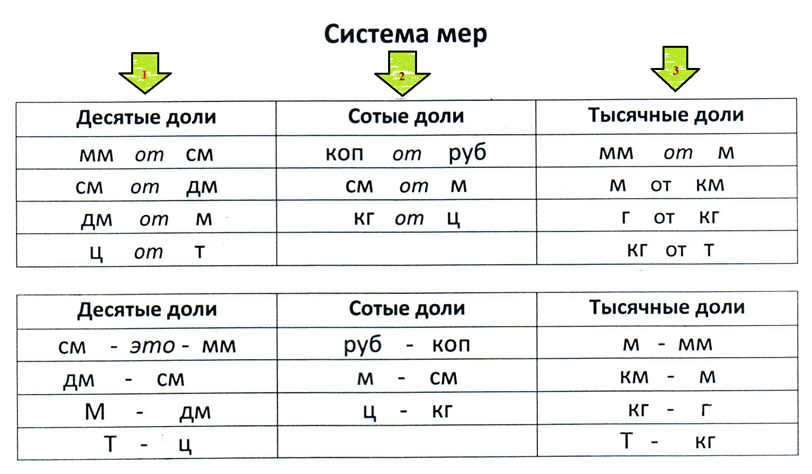
Рис. 11
При изучении тем «Площади» и «Объемы» составляется похожая таблица замены целых чисел десятичными дробями (см. рис. 12).
Образец записи:
9 га 1 м2 = 9 га 0001 м2 = 9, 0001 га
1 га = 10 000 м2
342 м2 = (354 : 100 ) а = 3, 54 а
1 а = 100 м2
23, 34 а = 23 а 34 м2
1 а = 100 м2
1 м2 = 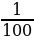 а = 0,01 а (две цифры после запятой)
а = 0,01 а (две цифры после запятой)
10, 3007 га = 10 га 3 007 м 2
1 га = 10 000 м2
1 м 2 = 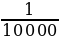 га = 0, 0001 га (четыре цифры после запятой)
га = 0, 0001 га (четыре цифры после запятой)
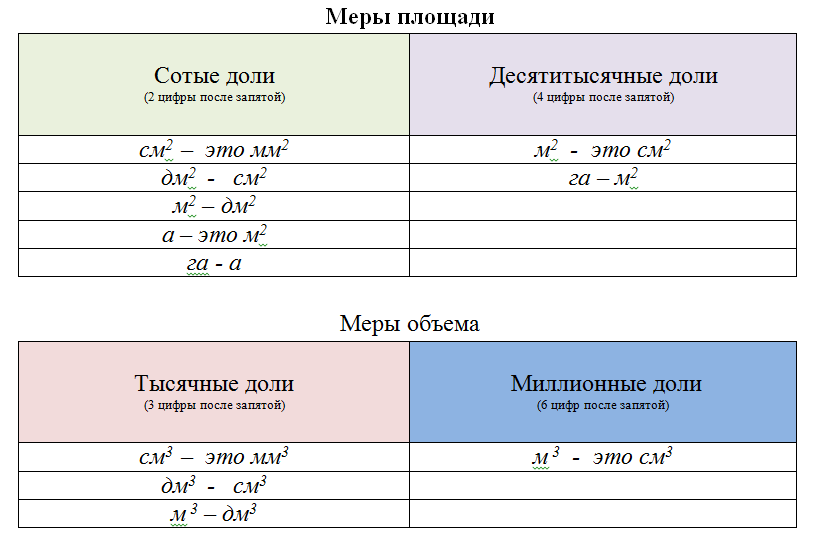
Рис. 12
Схемы и таблицы выглядит логичнее, а потому более ясны и легче запоминаются. В памятке также приведены справочные материалы по данной теме, традиционно записывающиеся в виде равенств и образцы вычислений при замене крупных мер мелкими и наоборот. Такие памятки применяются не только в классе, но и при выполнении домашней работы. Учащиеся могут их записать в свои индивидуальные книжки-памятки. Сложная тема становится простой и понятной.























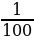 а = 0,01 а (две цифры после запятой)
а = 0,01 а (две цифры после запятой)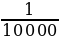 га = 0, 0001 га (четыре цифры после запятой)
га = 0, 0001 га (четыре цифры после запятой)










