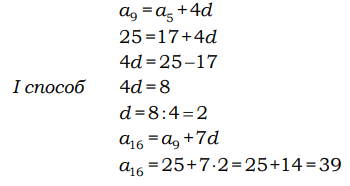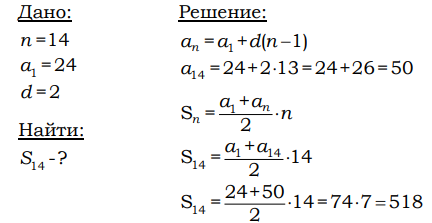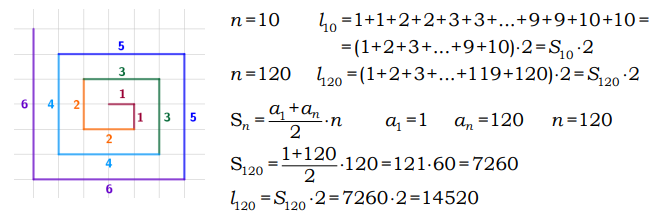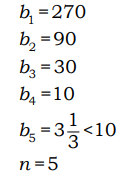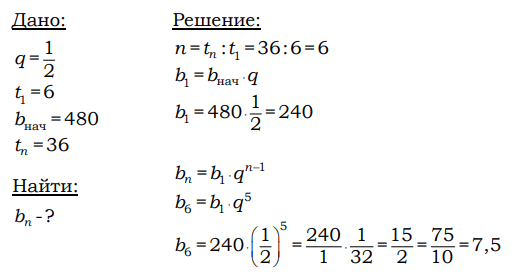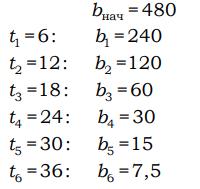| Задачи на прогрессии (№14) можно решить по следующему алгоритму: -
Внимательно прочитать задачу. -
Определить вид прогрессии (арифметическая или геометрическая). -
Определить известные элементы и что необходимо найти. -
По справочным материалам найти необходимую формулу. -
Решить задачу, используя формулы и данные. | 1. В амфитеатре 15 рядов. В первом ряду 28 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в двенадцатом ряду амфитеатра? Дано: 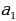 =28, d=3 =28, d=3 Найти: 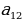 . . Решение: 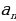 = =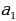 +d(n-1); +d(n-1); 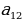 =28+3(12-1)=28+3·11=28+33=61. =28+3(12-1)=28+3·11=28+33=61. Ответ: 61.
2. В амфитеатре 16 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 17 мест, а в девятом ряду 25 мест. Сколько мест в последнем ряду амфитеатра? Дано: n=16, 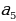 =17, =17, 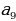 =25 =25 Найти: 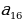 . . Решение: 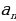 = =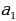 +d(n-1); +d(n-1); 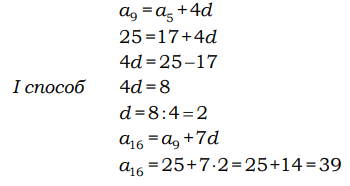

Ответ: 39.
3. В амфитеатре 14 рядов. В первом ряду 24 места, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре? 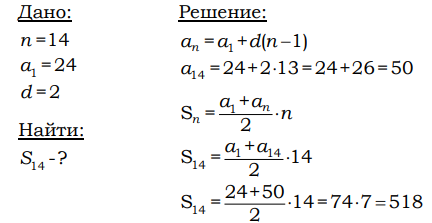
Ответ: 518.
4. В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 15 квадратных столиков вдоль одной линии? 
 
Ответ: 32.
5. На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 120. 
Решение: 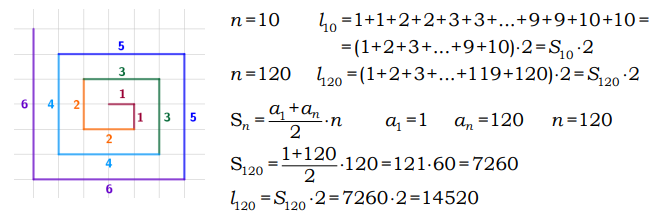 Ответ: 14520.
6. У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 270 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 10 см? 
Также данную задачу можно решить методом подбора: 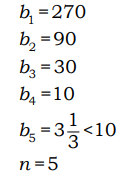
Ответ: 5.
7. В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 480 мг. Найдите массу изотопа через 36 минут. Ответ дайте в миллиграммах. 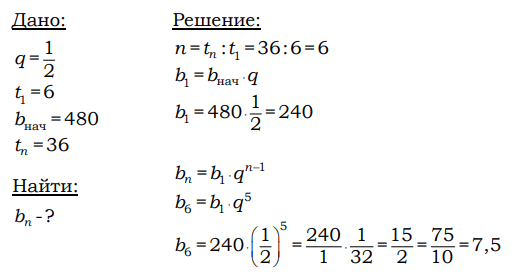
Также данную задачу можно решить методом подбора: 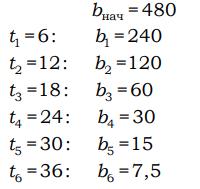
Ответ: 7,5. | 1) В амфитеатре 13 рядов. В первом ряду 22 места, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в одиннадцатом ряду амфитеатра? 2) При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7 ° C. Найдите температуру вещества (в градусах Цельсия) через 5 минут после начала проведения опыта, если его начальная температура составляла − 7 ° C. 3) В амфитеатре 16 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В четвёртом ряду 23 места, а в восьмом ряду 35 мест. Сколько мест в последнем ряду амфитеатра? 4) В амфитеатре 14 рядов. В первом ряду 16 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре? 5) Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 11 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые четыре секунды? 6) В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 24 квадратных столика вдоль одной линии? 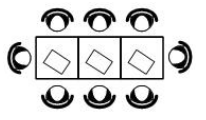 7) На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 110. 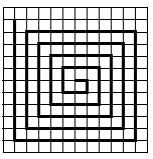 8) У Юли есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 450 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 20 см? 9) В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б. В начальный момент масса изотопа А составляла 480 мг. Найдите массу образовавшегося изотопа Б через 35 минут. Ответ дайте в миллиграммах. В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б. В начальный момент масса изотопа А составляла 480 мг. Найдите массу образовавшегося изотопа Б через 35 минут. Ответ дайте в миллиграммах. 10) В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 17 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 60 минут после начала эксперимента. Ответ дайте в миллиграммах. |







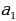 =28, d=3
=28, d=3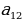 .
.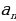 =
=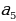 =17,
=17, 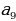 =25
=25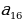 .
.