КИМ для прохождения
промежуточной аттестации по предмету «Геометрия»
9 класс
Цель: установление соответствия уровня и качества подготовки обучающихся 9 классов по предмету «Геометрия» объему, установленному обязательным минимумом содержания ООП.
Форма работы: контрольная работа
Структура работы:
Количество вариантов: 2
Каждый вариант работы содержит 2 части.
Первая часть содержит 5 заданий по геометрии базового уровня сложности. Эти задания направлены на проверку усвоения основных свойств, понятий, владения основными алгоритмами, умения решать простейшие задачи.
Каждое задание первой части оценивается в 1 балл.
Вторая часть содержит 2 задания по геометрии повышенного уровня сложности. При выполнении этих заданий проверяется умение учащихся применять знания в несколько измененной ситуации. В заданиях второй части учащиеся должны записать решение и обосновать его.
Каждое задание второй части оценивается в 2 балла.
Критерии оценивания:
| «5» | «4» | «3» | «2» |
| 8 – 9 баллов | 6 – 7 баллов | 4 – 5 баллов | 0 – 3 балла |
Аттестационная работа
В – 1
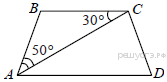
1. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
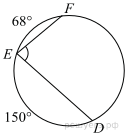
2. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
3. Периметр квадрата равен 40. Найдите площадь квадрата.
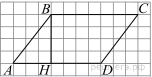
4. На рисунке изображен параллелограмм  . Используя рисунок, найдите
. Используя рисунок, найдите  .
.
5. Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
Если утверждений несколько, запишите их номера в порядке возрастания
6. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34.
7. В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.

В - 2
1. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
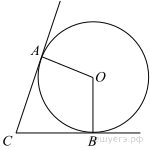
2. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
3. Основания трапеции равны 1 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
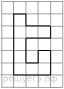
4. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
5. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите их номера в порядке возрастания.
6. Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 24, а расстояние от центра окружности до хорд АВ и CD равны соответственно 16 и 12.
7. В параллелограмме ABCD проведены высоты BE и BF. Докажите, что треугольник АВЕ подобен треугольнику СВF.

Ответы.
| № задания | В - 1 | В - 2 |
| 80 | 60 |
| 71 | 97 |
| 100 | 5,5 |
| 0,6 | 10 |
| 1 и 3 | 2 и 3 |
| 68 | 32 |
| Доказательство | Доказательство |
























