|
Задачи по курсу геометрии 7 класса
| № 1 Найдите углы треугольника, если они пропорциональны числам 2, 3, 7.
| № 2 Докажите, что в равнобедренном треугольнике с углом при вершине в 50 боковая сторона не равна основанию. |
| № 3 Один из углов неравнобедренного треугольника равен 80. Докажите, что в этом треугольнике не может быть угла, равного 50.
| № 4 В АВС один угол равен 45. В равном ему треугольнике есть угол в 38. Найдите два других угла АВС. | № 5 Один из углов прямоугольного треугольника равен 30, а сумма гипотенузы и меньшего из катетов равна 30 см. Найдите гипотенузу треугольника. |
| № 6 Один из углов прямоугольного треугольника равен 35. Найдите величины углов, которые образует биссектриса прямого угла с гипотенузой. | № 7 Из вершины прямого угла треугольника АВС проведена высота СD. Найдите BCD, зная, что А=40. | № 8 Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.
|
| № 9 Постройте равнобедренный треугольник по его основанию и высоте, проведенной к основанию.
| № 10 Медиана ВЕ АВС продолжена на отрезок ЕD, равный ВЕ. Докажите, что АВ DC. | № 11 Через вершину А АВС проведена прямая, параллельная стороне ВС, и через вершину С – прямая, параллельная АВ. Докажите, что проведенные прямые пересекаются и что получившийся треугольник равен данному.
|
| № 12 Один из углов треугольника равен 70. Определите угол между биссектрисами двух других углов этого треугольника. | № 13 Биссектриса равнобедренного треугольника, проведенная из вершины при основании, образует с противолежащей стороной углы, равные 30 и 150. Найдите углы данного равнобедренного треугольника. | № 14 Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.
|
| № 15 Постройте равнобедренный треугольник по его медиане, проведенной к основанию и углу при вершине.
| № 16 Постройте треугольник по двум сторонам и высоте, опущенной на третью сторону. | № 17 Постройте прямоугольный треугольник по гипотенузе и катету.
|
Ответы к заданиям книжки «Задачи по курсу геометрии 7 класса»
1) Решение: 2х + 3х + 7х = 180, 12х = 180, х = 180 : 12, х = 15.
15 . 2= 30, 15 . 3 = 45, 15 . 7 = 105
Ответ: 30, 45, 105.
2) Доказательство: 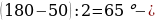 угол при основании. Угол при основании не равен углу при вершине. Следовательно, боковая сторона не равна основанию. Что и требовалось доказать.
угол при основании. Угол при основании не равен углу при вершине. Следовательно, боковая сторона не равна основанию. Что и требовалось доказать.
3) Доказательство: Предположим, что в треугольнике есть угол, равный 50. Тогда третий угол треугольника: 180 – (80 + 50) = 50, т.е. треугольник равнобедренный, что противоречит условию Значит, в этом треугольнике не может быть угла, равного 50. Что и требовалось доказать.
Значит, в этом треугольнике не может быть угла, равного 50. Что и требовалось доказать.
4) Решение: Один из углов по условию 45, второй 38, тогда 180 – (45 + 38) = 97– третий угол 
Ответ: 38, 97.
5) Решение: Пусть гипотенуза треугольника равна х. Катет, лежащий против угла 30 в прямоугольном треугольнике, равен половине гипотенузы, значит, меньший катет равен 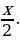 По условию сумма гипотенузы и меньшего из катетов равна 30 см. Значит,
По условию сумма гипотенузы и меньшего из катетов равна 30 см. Значит, 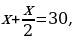
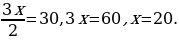 Итак, гипотенуза равна 20 см.
Итак, гипотенуза равна 20 см.
Ответ: 20 см.
6) Решение: По условию один из острых углов прямоугольного треугольника равен 35, тогда другой острый угол: 90 – 35 = 55. Биссектриса прямого угла делит его на два угла по 45. Тогда 180 – (35 + 45) = 100, 180 – (55 + 45) = 80 – искомые углы.
Ответ: 100, 80.
7) Решение: В АВС В = 180 – (90 + 40) = 50. В СDB ВCD = 180 – (90 + 50) = 40.
Ответ: 40.
8) Доказательство: В АВС AB = BC, значит, А = С = α, а В = 180 – 2α. Пусть СВD – внешний угол, ВЕ – биссектриса СВD.
В + СВD = 180 (смежные углы). СВD = 180 – В = 180 – (180 – 2α) = 2α, тогда DBE = 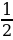 СВD = α, т.к. ВЕ – биссектриса СВD.
СВD = α, т.к. ВЕ – биссектриса СВD.
А = DBE, а это углы соответственные при прямых ВЕ и АС и секущей АD, значит,
ВЕ АС. Что и требовалось доказать.
10) Доказательство: ВЕ – медиана, следовательно, АЕ = ЕС. ВЕ = ЕD по условию.
АЕВ = СЕD как вертикальные. Значит, АВЕ = DЕС по двум сторонам и углу между ними. Тогда ВАЕ = DСЕ, а они накрест лежащие при прямых АВ и СD и секущей АС. Следовательно, АВ СD. Что и требовалось доказать.
11) Доказательство: Предположим, что проведенные прямые не пересекаются, то есть параллельны. Тогда параллельны и стороны ВС и АВ АВС, что невозможно.
Пусть проведенные прямые пересекаются в точке К. АК ВС, АС – секущая, значит, КАС = ВСА (накрест лежащие). Аналогично СК АВ, АС – секущая, значит,
АСК = ВАС (накрест лежащие).
Рассмотрим АВС и АКС, АС – общая сторона, ВСА = КАС, ВАС = АСК. Следовательно, АВС = АКС по стороне и двум прилежащим углам. Что и требовалось доказать.
12) Решение: Пусть в АВС А = 70, ВЕ и СК – биссектрисы углов В и С соответственно.
ВЕ СК =О.
В АВС АВС + АСВ = 180 – 70 = 110.
В ВОС ОВС + ВСО = 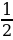 АВС +
АВС + 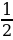 АСВ =
АСВ = 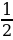 (АВС + АСВ) =
(АВС + АСВ) = 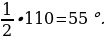
Тогда ВОС = 180 – 55 = 125.
Ответ: 125.
13) Решение: Пусть в АВС АВ = ВС, АD – биссектриса А, АDC = 150, ADB = 30.
BCA = BAC = x – углы при основании равнобедренного АВС. BAD = DAC = 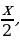 так как АD – биссектриса ВАС.
так как АD – биссектриса ВАС.
DАC + DCА + АDC = 180 – сумма углов АDC, 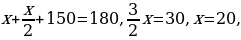 т.е. BAC = BCA = 20. АВС = 180 – (20 + 20) = 140.
т.е. BAC = BCA = 20. АВС = 180 – (20 + 20) = 140.
Ответ: 20, 20, 140.
1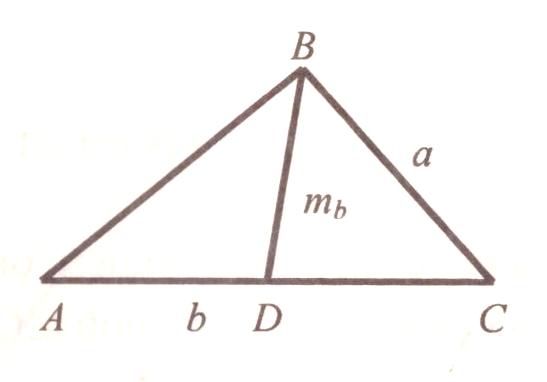 4) Анализ:
4) Анализ:
Построение.
1. Построим на произвольной прямой от произвольной точки А отрезок АС = b.
2. Разделим отрезок АС пополам: AD = DC.
3. Из точки D как из центра проводим окружность с радиусом R = mb.
4. Из точки С как из центра проводим окружность радиусом а.
5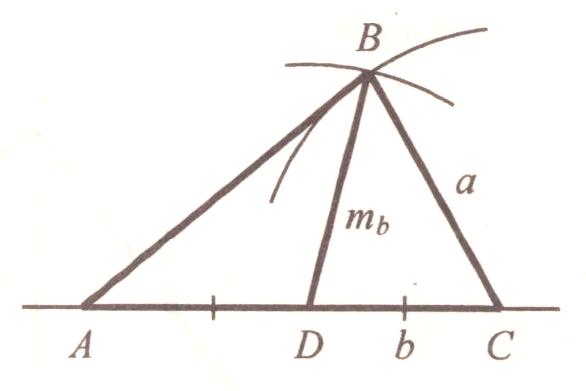 . Обозначим через В одну из точек пересечения окружностей и соединим точки В и А, В и С. АВС – искомый.
. Обозначим через В одну из точек пересечения окружностей и соединим точки В и А, В и С. АВС – искомый.
Доказательство.
В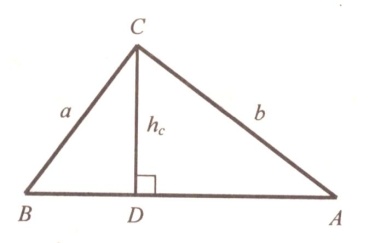 АВС АС = b по построению; AD = DC, значит, BD – медиана, BD = mb по построению; ВС = а также по построению, значит АВС отвечает всем условиям задачи.
АВС АС = b по построению; AD = DC, значит, BD – медиана, BD = mb по построению; ВС = а также по построению, значит АВС отвечает всем условиям задачи.
16) Анализ:
Построение.
1. Строим произвольную прямую d и отмечаем на ней произвольную точку D.
2. Через точку D проводим прямую c d.
3. Откладываем на прямой с DC = hc.
4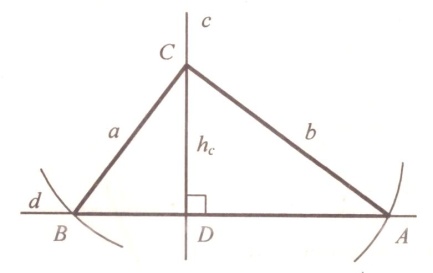 . Из точки С как из центра описываем две окружности с радиусом R1 = b и R2 = a до их пересечения с прямой d в точках А и В. АВС – искомый, так отвечает всем условиям задачи.
. Из точки С как из центра описываем две окружности с радиусом R1 = b и R2 = a до их пересечения с прямой d в точках А и В. АВС – искомый, так отвечает всем условиям задачи.
1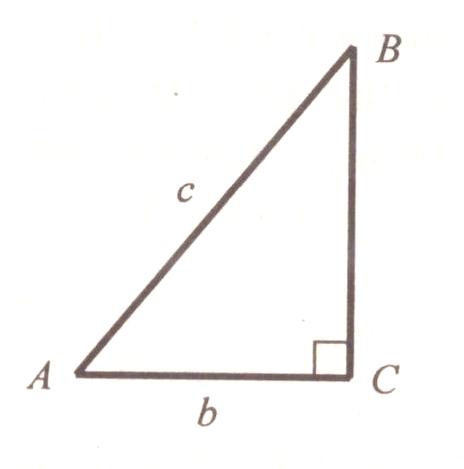 7) Анализ:
7) Анализ:
Построение.
1. Построим С = 90.
2. На одной из сторон С отложим от вершины С отрезок СА = b.
3. Из точки А как из центра опишем окружность радиусом R = c до пересечения со второй стороной. АВС – искомый.
Д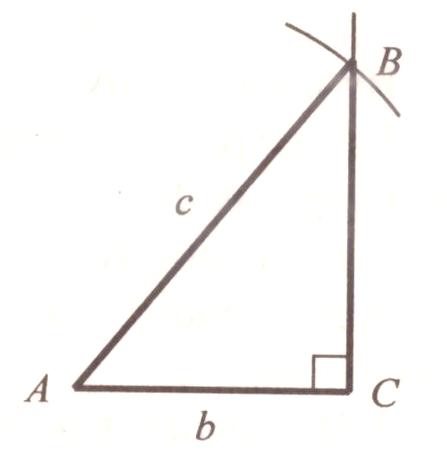 оказательство.
оказательство.
АВС – прямоугольный, так как ВСА = 90 по построению. По построению же катет АС = b и гипотенуза АВ = с, значит, АВС отвечает всем условиям задачи.







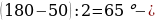 угол при основании. Угол при основании не равен углу при вершине. Следовательно, боковая сторона не равна основанию. Что и требовалось доказать.
угол при основании. Угол при основании не равен углу при вершине. Следовательно, боковая сторона не равна основанию. Что и требовалось доказать. Значит, в этом треугольнике не может быть угла, равного 50. Что и требовалось доказать.
Значит, в этом треугольнике не может быть угла, равного 50. Что и требовалось доказать.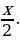 По условию сумма гипотенузы и меньшего из катетов равна 30 см. Значит,
По условию сумма гипотенузы и меньшего из катетов равна 30 см. Значит, 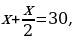
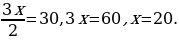 Итак, гипотенуза равна 20 см.
Итак, гипотенуза равна 20 см.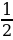 СВD = α, т.к. ВЕ – биссектриса СВD.
СВD = α, т.к. ВЕ – биссектриса СВD. 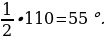
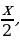 так как АD – биссектриса ВАС.
так как АD – биссектриса ВАС.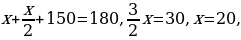 т.е. BAC = BCA = 20. АВС = 180 – (20 + 20) = 140.
т.е. BAC = BCA = 20. АВС = 180 – (20 + 20) = 140. 4) Анализ:
4) Анализ: . Обозначим через В одну из точек пересечения окружностей и соединим точки В и А, В и С. АВС – искомый.
. Обозначим через В одну из точек пересечения окружностей и соединим точки В и А, В и С. АВС – искомый. АВС АС = b по построению; AD = DC, значит, BD – медиана, BD = mb по построению; ВС = а также по построению, значит АВС отвечает всем условиям задачи.
АВС АС = b по построению; AD = DC, значит, BD – медиана, BD = mb по построению; ВС = а также по построению, значит АВС отвечает всем условиям задачи. . Из точки С как из центра описываем две окружности с радиусом R1 = b и R2 = a до их пересечения с прямой d в точках А и В. АВС – искомый, так отвечает всем условиям задачи.
. Из точки С как из центра описываем две окружности с радиусом R1 = b и R2 = a до их пересечения с прямой d в точках А и В. АВС – искомый, так отвечает всем условиям задачи. 7) Анализ:
7) Анализ: оказательство.
оказательство.















