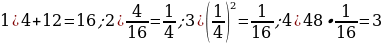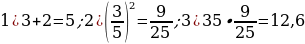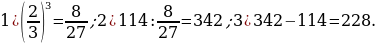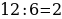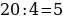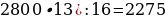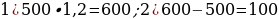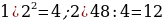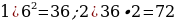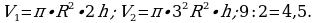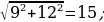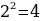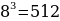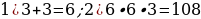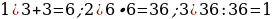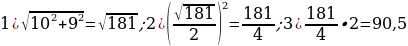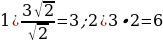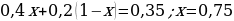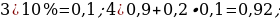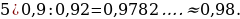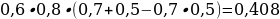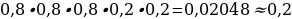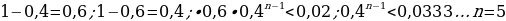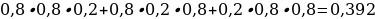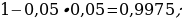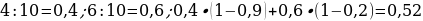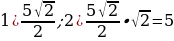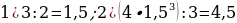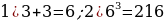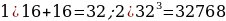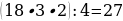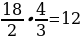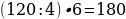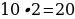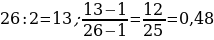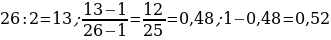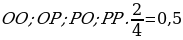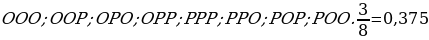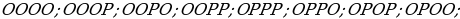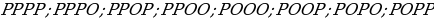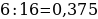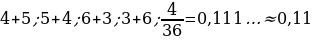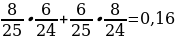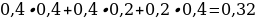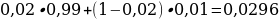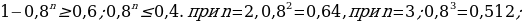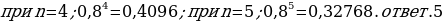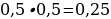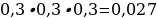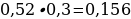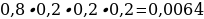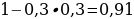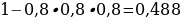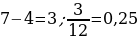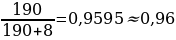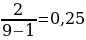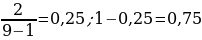Профиль 1 (шаблон решения) 2023.
1). В треугольнике ABC угол A или угол В равен 37°, стороны AC и BC равны. Найдите угол C. 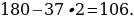
2). В треугольнике ABC угол С равен 102°, стороны AC и BC равны. Найдите угол А или В 
3). В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. 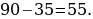
4). В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника . 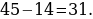
5). Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 12°. Найдите меньший угол прямоугольного треугольника. 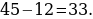
6). Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. 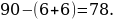
7). В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 5°. Найдите угол B. 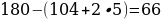
8). В остроугольном треугольнике ABC угол A равен 62°, BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. 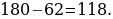
9). В треугольнике ABC угол C равен 58°, биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. 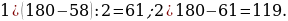
10). Один угол параллелограмма больше другого на 40°. Найдите меньший угол. 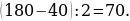
11). Один угол параллелограмма больше другого на 52°. Найдите больший угол. 64 + 52 = 116.
64 + 52 = 116.
12). В ромбе ABCD угол DAB равен 148°. Найдите угол BDC.
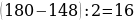
13). В ромбе ABCD угол BCD равен 48°. Найдите угол DBA.
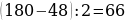
35). Заказ на 140 деталей первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 4 детали больше? 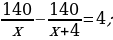 ответ.
ответ. 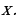
36). Заказ на 176 деталей первый рабочий выполняет на 5 часов быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 5 деталей больше, чем второй?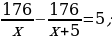 ответ.
ответ. 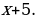
37). На изготовление 720 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 840 деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей в час делает первый рабочий?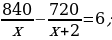 ответ.
ответ. 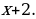
38). На изготовление 696 деталей первый рабочий затрачивает на 5 часов меньше, чем второй рабочий на изготовление 725 деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает второй рабочий? 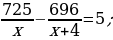 ответ.
ответ. 
39). Первая труба пропускает на 8 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем вторая труба? 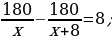 ответ.
ответ. 
40). Первая труба пропускает на 4 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 252 литров она заполняет на 4 минут быстрее, чем первая труба? 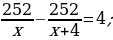 ответ.
ответ. 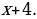
41). Первая труба наполняет резервуар на 13 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 42 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
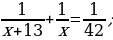 ответ.
ответ. 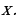
42). Один мастер может выполнить заказ за 30 часов, а другой — за 15 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
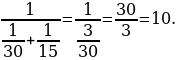
14). Стороны параллелограмма равны 9 и 15. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите высоту, опущенную на большую сторону параллелограмма. 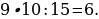
15). Площадь параллелограмма ABCD равна 142. Точка H — середина стороны AD. Найдите площадь трапеции BHDC. 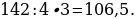
16). Две стороны треугольника равны 20 и 35. Высота, опущенная на большую из этих сторон, равна 24. Найдите высоту, опущенную на меньшую из этих сторон треугольника. 
17). Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 13. Найдите площадь этого треугольника. 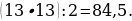
18). В равностороннем треугольнике ABC высота CH равна 27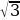 . Найдите AB.
. Найдите AB. 
19). Площадь треугольника ABC равна 36, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE. 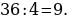
20). Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции АВЕD. 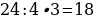
21). В треугольнике ABC, DE — средняя линия. Площадь треугольник, а CDE равна 24. Найдите площадь треугольника ABC. 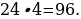
22). В треугольнике ABC AC=BC=16, AB=8. Найдите cosA. 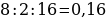
23). В треугольнике ABC угол C равен 90°, ВС=12, 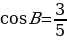 . Найдите АВ.
. Найдите АВ. 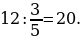
24). В треугольнике ABC угол C равен 90°, AB=10, AC= 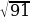 . Найдите sinA.
. Найдите sinA. 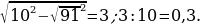
25). В треугольнике ABC угол C равен 90°, AB=6, BC=  . Найдите cosA.
. Найдите cosA. 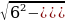
26). В треугольнике ABC угол C равен 90°, BC=6, AB=10. Найдите sinB.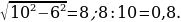
27). В треугольнике ABC угол C равен 90°, AC=10, tgA = 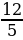 . Найдите AB.
. Найдите AB. 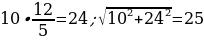
28). В треугольнике ABC AC=BC, высота CH равна 7,2, cosA =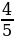 . Найдите AC.
. Найдите AC. 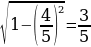 ;
; 
29). В треугольнике ABC AC=BC, AB=20, высота AH равна 8. Найдите синус угла BAC. 
30). В треугольнике ABC AB=BC, AC=14, высота CH равна 7. Найдите синус угла ACB.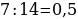
31). В треугольнике ABC AC=BC, AB=8, AH — высота, BH=2. Найдите косинус угла BAC.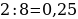
32). В треугольнике ABC AC=BC, AB=5, высота AH равна 4. Найдите синус угла BAC. 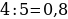
33). Найдите центральный угол, если он 28° больше вписанного угла. Ответ дайте в градусах. 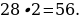
33). Центральный угол на 32° больше вписанного угла. Найдите вписанный угол. Ответ. 32.
34). Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 130°. Найдите вписанный угол ACB. 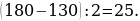
35).Отрезки AC и BD диаметры окружности с центром O. Угол ACB равен 56°. Найдите угол AOD.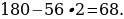
36). Найдите вписанный угол, опирающийся на дугу, равную 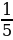 окружности.
окружности. 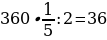 .
.
37). На окружности отмечены точки A, B и C. Дуга окружности AC, не содержащая точку B, составляет 120°. Дуга окружности BC, не содержащая точку A, составляет 82°. Найдите вписанный угол ACB.
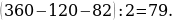
38). Угол ACO равен 27°, где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B (см. рис.). Найдите величину меньшей дуги AB окружности. 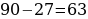
29). Теплоход проходит по течению реки до пункта назначения 468 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода равна 22 км/ч, стоянка длится 3 часа, а в пункт отправления теплоход возвращается через 47 часов.
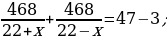 ответ.
ответ. 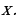
30). Моторная лодка прошла против течения реки 165 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.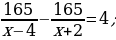 ответ.
ответ. 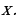
31). Моторная лодка прошла против течения реки 252 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 16 км/ч. Ответ дайте в км/ч. 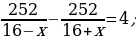 ответ.
ответ. 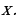
32). Байдарка в 10 : 00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки равна 2 км/ч.
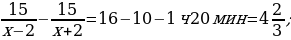 ответ.
ответ. 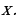
33). Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 4 часа, баржа отправилась назад и вернулась в пункт А в 22:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 8 км/ч.
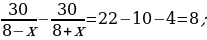 ответ.
ответ. 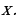
34). Расстояние между пристанями A и B равно 192 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 92 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
 ответ.
ответ. 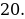
24). По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
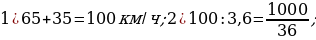
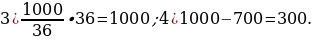
25). От пристани A к пристани B, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов после этого следом за ним со скоростью на 8 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч. 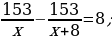 ответ.
ответ. 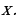
26). Пристани A и B расположены на озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью из A в 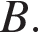 На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в
На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в 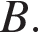 Найдите скорость баржи на пути из A в
Найдите скорость баржи на пути из A в 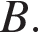 Ответ дайте в км/ч.
Ответ дайте в км/ч. 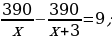 ответ.
ответ. 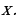
27). Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?
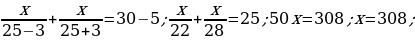
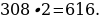
28). Теплоход проходит по течению реки до пункта назначения 384 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 48 часов. Ответ дайте в км/ч. 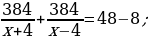 ответ.
ответ. 
39). Угол ACO равен 28°. Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D (см. рис.). Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах. 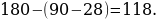
40). Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна 58°. Найдите угол ACB. 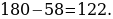
41). Угол ACB равен 54°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 138°. Найдите угол DAE. 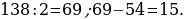
42). В четырёхугольник ABCD вписана окружность, AB=13, BC=7 и AD=11. Найдите четвёртую сторону четырёхугольника. 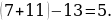
43). В четырёхугольник ABCD вписана окружность, AB=22, CD=17. Найдите периметр четырёхугольника ABCD. 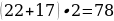
44). Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
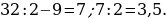
45). Боковые стороны трапеции, описанной около окружности, равны 15 и 22. Найдите среднюю линию трапеции. 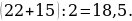
46). Четырёхугольник ABCD вписан в окружность. Угол ABD равен 61°, угол CAD равен 37°. Найдите угол ABC. 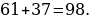
47). Четырёхугольник ABCD вписан в окружность. Угол ABC равен 56°, угол CAD равен 42°. Найдите угол ABD. 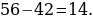
48). В четырёхугольник ABCD вписана окружность, угол BAD равен 136° . Найдите угол BCD. 180-136=44.49). Два угла вписанного в окружность четырёхугольника равны 59° и 83°. Найдите меньший из оставшихся углов. 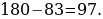
50). Два угла вписанного в окружность четырёхугольника равны 78° и 113°. Найдите больший из оставшихся углов.
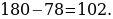
Профиль 2 (шаблон решения)
1). В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=6, CD=17, AD=6. Найдите длину диагонали CA1. 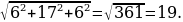
2). Диагональ куба равна 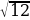 . Найдите его объем.
. Найдите его объем. 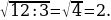
3). В прямоугольном параллелепипеде известны длины рёбер: АВ = 3, АD = 5, A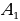 = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
= 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1. 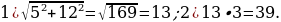
4)В прямоугольном параллелепипеде известны длины рёбер: АВ = 21, АD = 20, A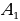 = 23. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, А1 и С.
= 23. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, А1 и С. 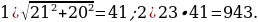
4)В прямоугольном параллелепипеде 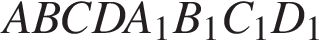 известны длины рёбер АВ = 27, АD = 36, A
известны длины рёбер АВ = 27, АD = 36, A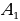 = 10. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки D, D1 и B.
= 10. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки D, D1 и B.
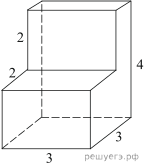
5). Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы – прямые). 

5). Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы – прямые). 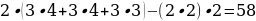
18). Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 143 км. На следующий день он отправился обратно в А со скоростью на 2 км/ч больше прежней. По дороге он сделал остановку на 2 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
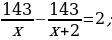 ответ.
ответ. 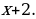
19). Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
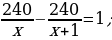 ответ.
ответ. 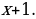
20). Два велосипедиста одновременно отправились в 88−километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч. 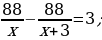 ответ.
ответ. 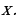
21). Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 70 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 10 минут позже автомобилиста. Ответ дайте в км/ч.
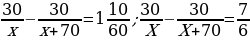 ответ.
ответ. 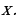
22). Расстояние между городами A и B равно 420 км. Из города A в город B выехал автомобиль, а через 1 час следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах. 
23). Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 12 часов раньше, чем велосипедист приехал в город А, а встретились они через 2 часа 30 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист? 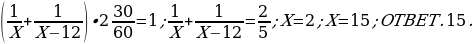
12). Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
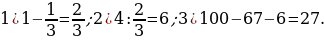
13). Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 
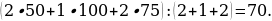
14). Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.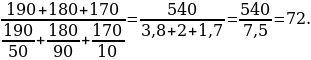
15). Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч?

16). Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города  Ответ дайте в км/ч.
Ответ дайте в км/ч. 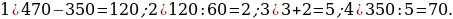
17). Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 187 км. На следующий день он отправился обратно в А со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
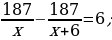 ответ.
ответ. 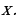
5). Найдите площадь поверхности многогранника, изображённого на рисунке 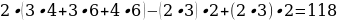
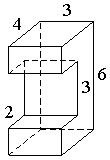
6). Найдите объём многогранника, изображённого на рисунке (все двугранные углы — прямые).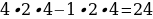

7). В кубе найдите угол между прямыми 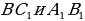 . Ответ. 90.
. Ответ. 90.
8). В кубе найдите угол между прямыми 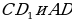 . Ответ. 90.
. Ответ. 90.
9). В кубе найдите угол между прямыми 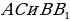 . Ответ. 90.
. Ответ. 90.
10). В кубе найдите угол между прямыми 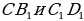 . Ответ. 90.
. Ответ. 90.
11). В кубе найдите угол между прямыми 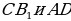 . Ответ. 45.
. Ответ. 45.
12). В кубе найдите угол между прямыми 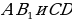 . Ответ. 45.
. Ответ. 45.
13). В кубе найдите угол между прямыми 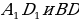 . Ответ. 90.
. Ответ. 90.
14). В кубе найдите угол между прямыми 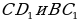 . Ответ. 60.
. Ответ. 60.
15).В прямоугольном параллелепипеде 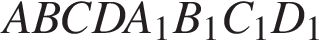 известны длины рёбер: АВ = 6, АD = 8, A
известны длины рёбер: АВ = 6, АD = 8, A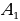 = 21. Найдите синус угла между прямыми
= 21. Найдите синус угла между прямыми 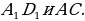
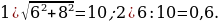
16).В прямоугольном параллелепипеде 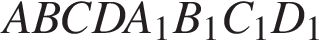 известны длины рёбер: АВ = 6, АD = 8, A
известны длины рёбер: АВ = 6, АD = 8, A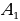 = 9. Найдите синус угла между прямыми
= 9. Найдите синус угла между прямыми 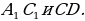
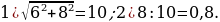
17).В прямоугольном параллелепипеде 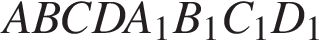 известны длины рёбер: АВ = 28, АD = 16, A
известны длины рёбер: АВ = 28, АD = 16, A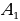 = 12. Найдите синус угла между прямыми
= 12. Найдите синус угла между прямыми 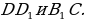
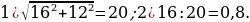
18). Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба. 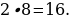
19). Объём куба равен 20.Найдите объем треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины. 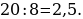
20). Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 4 и 7, боковое ребро призмы равно 6. Найдите объём призмы. 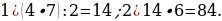
21). Площадь боковой поверхности треугольной призмы равна 75. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы. 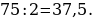
22). Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы. 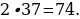
23). Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. 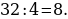
24). Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5. 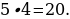
25). Найдите объём многогранника, вершинами которого являются точки D, E, F, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 8, а боковое ребро равно 9. 
6). Имеется два сплава. Первый сплав содержит 5% меди, второй − 30% меди. Из этих двух сплавов получили третий сплав массой 100кг, содержащий 20% меди. На сколько кг масса первого меньше массы второго сплава?
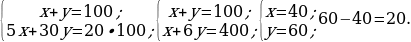
7). Имеется два сосуда. Первый содержит 60 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 45% кислоты. Сколько процентов кислоты содержится в первом сосуде?
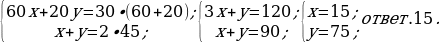
8). Смешав 24-процентный и 67-процентный растворы кислоты и добавив 10 кг чистой воды, получили 41-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси? Ответ. 60.
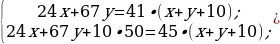
9). В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 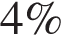 дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
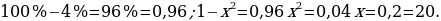
10). Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 78 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
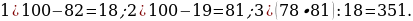
11). Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов одиннадцать таких же рубашек дороже куртки?
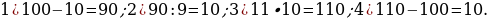
46). Платежный терминал в течение рабочего дня может выйти из строя. Вероятность этого события 0,07. В торговом центре независимо друг от друга работают два таких платёжных терминала. Найдите вероятность того, что хотя бы один из них в течение рабочего дня будет исправен.
Профиль – 9. ( шаблон решения)
1). В сосуд, содержащий 5 литров 12−процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
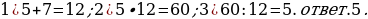
2). Смешали некоторое количество 15−процентного раствора некоторого вещества с таким же количеством 19−процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? 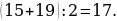
3). Смешали 4 литра 15−процентного водного раствора некоторого вещества с 6 литрами 25−процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
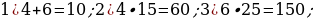
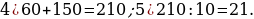
4). Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава.
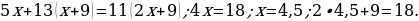
5). Первый сплав содержит 40% меди, второй — 25% меди. Масса первого сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава.
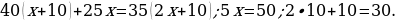
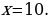 ответ.30.
ответ.30.
26). Найдите объём многогранника, вершинами которого являются вершины A, C, D, F, A1, C1, D1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11. 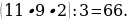
27). Найдите объём многогранника, вершинами которого являются точки D, A1, B1, C1, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 2. 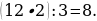
28). Найдите объём многогранника, вершинами которого являются вершины A1, B1, F1, A правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 15. 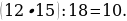
29). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SD=26, AC=20. Найдите длину отрезка SO.
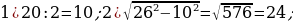
30). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=21, AC=40. Найдите длину отрезка SB.
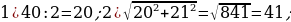
31). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=48, SC=73. Найдите длину отрезка AC. 
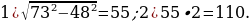
32). В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды. 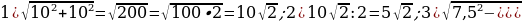
33). В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC равно 37, сторона основания равна 35 . Найдите объём пирамиды.
. Найдите объём пирамиды. 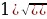
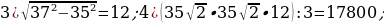
34). В правильной четырёхугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите её объём.

35). В правильной четырёхугольной пирамиде все ребра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых ребер. 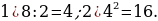
36). Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.
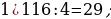
37). Объём треугольной пирамиды равен 78. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рисунок). Найдите объём отсечённой треугольной пирамиды.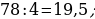
38). В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды. 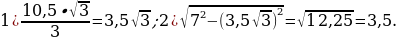
39). В правильной шестиугольной пирамиде боковое ребро равно 6,5, а сторона основания равна 2,5. Найдите высоту пирамиды. 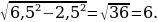
40). Высота конуса равна 12, а диаметр основания равен 70. Найдите длину образующей конуса. 
41). Высота конуса равна 24, а длина образующей равна 25. Найдите диаметр основания конуса. 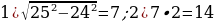
42). Диаметр основания конуса равен 18, а длина образующей равна 41. Найдите высоту конуса. 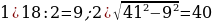
43). Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 9. Найдите объём цилиндра. 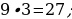
44). Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 18. Найдите объём конуса. 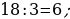
45). Диаметр основания конуса равен 140, а длина образующей равна 74. Найдите площадь осевого сечения конуса.
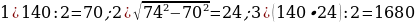
38). Первый игральный кубик обычный, а на гранях второго кубика числа 1 и 2 встречаются по три раза. В остальном кубики одинаковые.Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 1 и 2 очков. Какова вероятность того, что бросали первый кубик? Ответ. 0,1
39). Первый игральный кубик обычный, а на гранях второго кубика нет нечётных чисел, а чётные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые.Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали второй кубик? Ответ. 0,8
40). Первый игральный кубик обычный, а на гранях второго кубика нет нечётных чисел, а чётные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые.Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик? Ответ. 0,2
41). Первый игральный кубик обычный, а на гранях второго кубика числа 5 и 6 встречаются по три раза. В остальном кубики одинаковые.Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 5 и 6 очков. Какова вероятность того, что бросали второй кубик? Ответ. 0,9
42). Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца? Ответ. 0,192
43). Артём гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану. Ответ. 0,3125
44). Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»? Ответ. 0,6
45). В городе 48 % взрослого населения — мужчины. Пенсионеры составляют 12,6 % взрослого населения, причём доля пенсионеров среди женщин равна 15 %. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером». Ответ. 0,1
29). Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. ООО, ООР, ОРО, ОРР, РРР, РРО, РОР, РОО. 1:8 = 0,125
30). Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).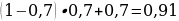
31). Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка. 6+2;2+6;3+5;5+3;4+4. 1:5 = 0,2 ответ. 0,5
32). При двукратном бросании игральной кости в сумме выпало 9 очков. Какова вероятность того, что хотя бы раз выпало 5 очков? 6+3; 3+6; 4+5; 5+4; 2:4 = 0,5 ответ. 0,5
33). Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых. 0,63
34). В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
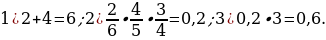
35). Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали второй кубик? Ответ. 0,8
36). Первый игральный кубик обычный, а на гранях второго кубика нет чисел, больших, чем 2, а числа 1 и 2 встречаются по три раза. В остальном кубики одинаковые.Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 1 и 2 очков. Какова вероятность того, что бросали второй кубик? Ответ. 0,9
37). Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В остальном кубики одинаковые.Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали первый кубик? Ответ . 0,2
46). Площадь основания конуса равна 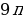 , высота 6. Найдите площадь осевого сечения.
, высота 6. Найдите площадь осевого сечения. 
47). Площадь основания конуса равна 48. Плоскость параллельная плоскости основания, делит его высоту на отрезки длиной 4 и 12, считая от вершины. Найдите площадь сечения конуса.
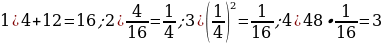
48). Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 6 раз, а высоту оставить прежней? 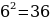
49). Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
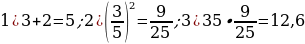
50). В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
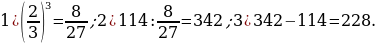
51). Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра. 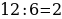
52). Площадь боковой поверхности цилиндра равна 20 π, а высота равна 4. Найдите диаметр основания. 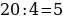
53). В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. ( 
54). В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объём детали. 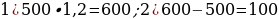
55). В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? 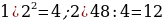
56). В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз меньше диаметра первого? Ответ выразите в сантиметрах.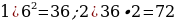
57). Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
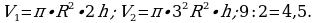
58). Радиусы двух шаров равны 9 и 12. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров. 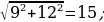
59). Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше второго. 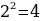
60). Дано два шара. Радиус первого шара в 8 раза больше радиуса второго. Во сколько раз объем первого шара больше второго. 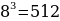
61). Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 3. Найдите объём параллелепипеда.
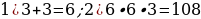
62). Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра. 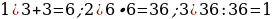
63). В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
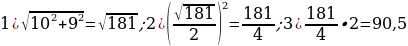
64). Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна 3√2. Найдите площадь боковой поверхности цилиндра.
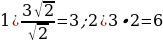
24). Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

25). Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.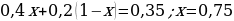
26). На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

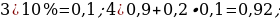
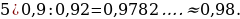
27). Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.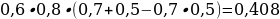
28). По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернетмагазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
18). Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.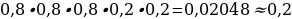
19). При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? 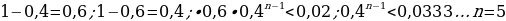
20). В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
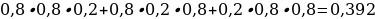
21). В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
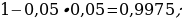
22). Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.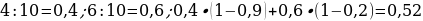
23). Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

65). Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 5√2. Найдите площадь боковой поверхности конуса. 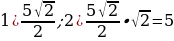
66). Куб с ребром 3 вписан в шар. Найдите объем этого шара.
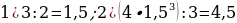
67). Куб описан около сферы радиуса 3. Найдите его объём.
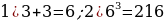
68). Прямоугольный параллелепипед описан около сферы радиуса 16. Найдите его объём. 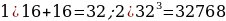
69). Шар, объём которого равен 18, вписан в цилиндр. Найдите объём цилиндра. 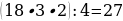
70). Цилиндр, объём которого равен 18, описан около шара. Найдите объём шара. 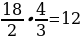
71). Шар вписан в цилиндр. Площадь поверхности шара равна 120. Найдите площадь полной поверхности цилиндра. 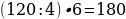
72). Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса. 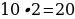
73). Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 50√2. Найдите радиус сферы. Ответ.50.
74). Конус вписан в шар (см. рисунок). Радиус основания конуса равен радиусу шара. Объём конуса равен 39. Найдите объём шара. 
Профиль 3 (шаблон решения) 2023
1). Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 16 спортсменов из России, в том числе Игорь Чаев. Какова вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.

2). В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе. 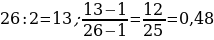
3). В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы по 13 человек. Найдите вероятность того, что Андрей и Сергей окажутся в разных группах.
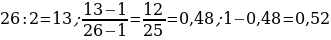
4). В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. 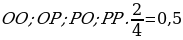
5). В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза. 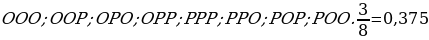
6). В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел выпадет ровно два раза.
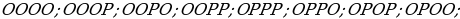
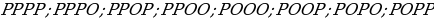
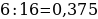
7). В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9очков. Округлите до сотых.
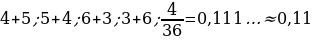
11). В коробке 8 синих, 6 красных и 11 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер? 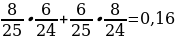
12). Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4. 1 - 0,4 – 0,4 = 0,2-ничья.
ВВ +ВН +НВ = 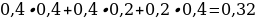
13). Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля. 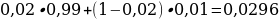
14). Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6? 1 –0,2=0,8
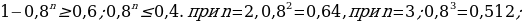
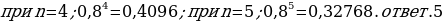
15). Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?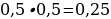
16). На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу  0,0625
0,0625
17). В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).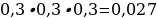
5). Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.
0,82 – 0,51 = 0,31
6). При выпечке хлеба производится контрольное взвешивание испеченной буханки. Известно, что вероятность того, что её масса окажется меньше 810 г, равна 0,97. Вероятность того, что её масса окажется больше 790 г, равна 0,91. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
1 – 0,97 = 0,03 1 – 0,91 = 0,09 1 – 0,03 – 0,09 = 0,88
6). В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,1. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,03. Найдите вероятность того, что к вечеру кофе останется в обоих автоматах.
0,1+0,1 – 0,03 = 0,17; 1 – 0,17 = 0,83
7). Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8». 2 и 6, 6 и 2, 4 и 4; 3:25 = 0,12
8). Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. 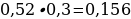
9). Стрелок стреляет по 4 одинаковым мишеням по одному разу, вероятность промаха 0,2, найдите вероятность что он попадёт в первую мишень, а в 3 оставшиеся промахнется. 1 – 0,2 = 0,8-попадание. 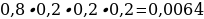
10). Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. 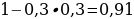
10). Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,8. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
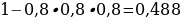
8). Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 4, но не дойдя до отметки 7 часов.
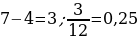
9). Фабрика выпускает сумки. В среднем на 190 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
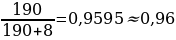
10). За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом. 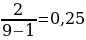
11). За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом . 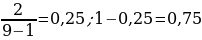
Профиль 4
1). На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. 0,2+0,15 = 0,35
2). Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше. 1 – 0,81 = 0,19
3). Вероятность того, что на тестировании по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. 0,74 – 0,67 =0,07
4). Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. 0,97 – 0,89 = 0,08





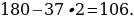
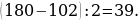
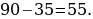
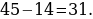
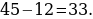
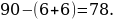
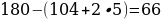
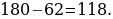
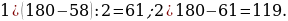
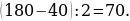
 64 + 52 = 116.
64 + 52 = 116.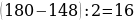
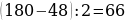
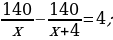 ответ.
ответ. 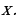
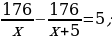 ответ.
ответ. 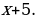
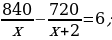 ответ.
ответ. 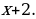
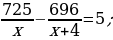 ответ.
ответ. 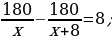 ответ.
ответ. 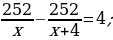 ответ.
ответ. 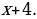
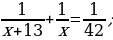 ответ.
ответ. 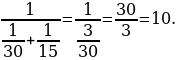
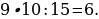
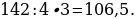

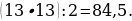
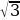 . Найдите AB.
. Найдите AB. 
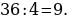
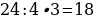
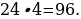
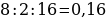
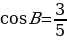 . Найдите АВ.
. Найдите АВ. 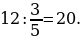
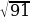 . Найдите sinA.
. Найдите sinA. 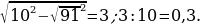
 . Найдите cosA.
. Найдите cosA. 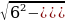
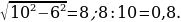
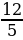 . Найдите AB.
. Найдите AB. 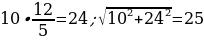
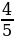 . Найдите AC.
. Найдите AC. 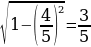 ;
; 
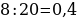
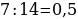
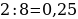
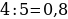
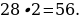
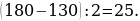
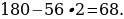
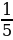 окружности.
окружности. 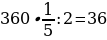 .
.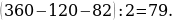
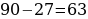
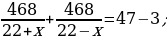 ответ.
ответ. 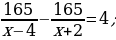 ответ.
ответ. 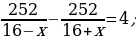 ответ.
ответ. 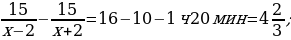 ответ.
ответ. 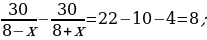 ответ.
ответ.  ответ.
ответ. 
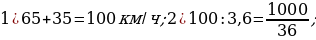
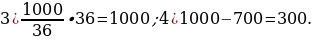
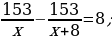 ответ.
ответ. 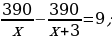 ответ.
ответ. 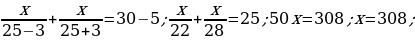
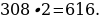
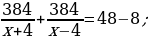 ответ.
ответ. 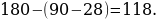
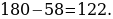
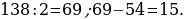
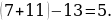
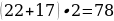
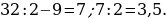

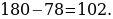
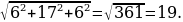
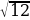 . Найдите его объем.
. Найдите его объем. 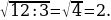
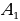 = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
= 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1. 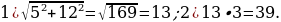
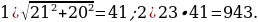
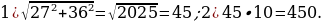
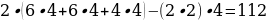

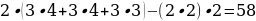

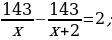 ответ.
ответ. 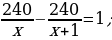 ответ.
ответ. 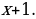
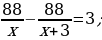 ответ.
ответ. 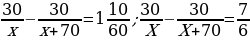 ответ.
ответ. 
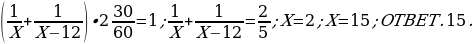
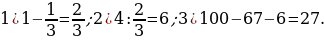
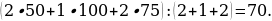
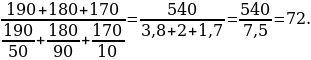

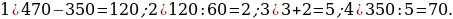
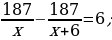 ответ.
ответ. 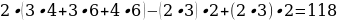

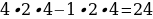

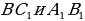 . Ответ. 90.
. Ответ. 90. 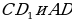 . Ответ. 90.
. Ответ. 90. 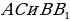 . Ответ. 90.
. Ответ. 90. 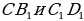 . Ответ. 90.
. Ответ. 90. 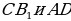 . Ответ. 45.
. Ответ. 45. 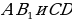 . Ответ. 45.
. Ответ. 45. 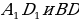 . Ответ. 90.
. Ответ. 90. 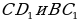 . Ответ. 60.
. Ответ. 60. 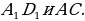
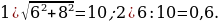
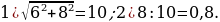
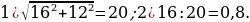
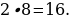
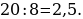
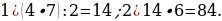
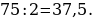
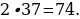
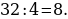
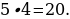

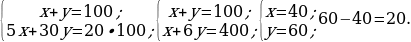
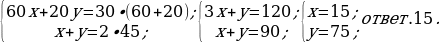
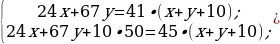
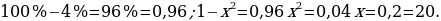
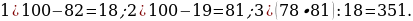
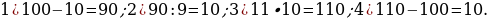
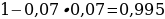
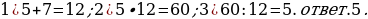
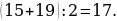
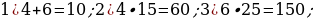
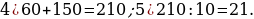
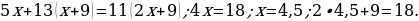
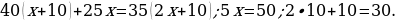
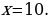 ответ.30.
ответ.30.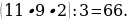
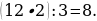
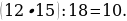
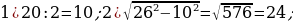
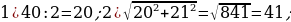
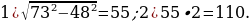
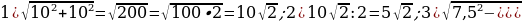
 . Найдите объём пирамиды.
. Найдите объём пирамиды. 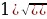
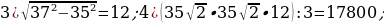

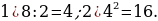
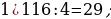
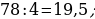
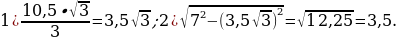
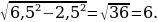

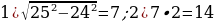
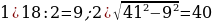
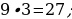
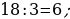
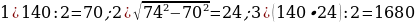
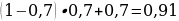
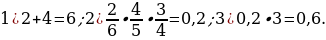
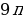 , высота 6. Найдите площадь осевого сечения.
, высота 6. Найдите площадь осевого сечения.