Колебательные и волновые процессы.

1. КОЛЕБАТЕЛЬНЫЕ И ВОЛНОВЫЕ ПРОЦЕССЫ.

   1. Механические и электромагнитные колебания.

1. Механические колебания

Многообразные движения тел в окружающем нас мире можно разделить на два класса в зависимости от того, остается ли тело в процессе движения вблизи некоторого среднего положения или такого положения нет. Мы обратимся к первому классу. Отличительной чертой многих движений рассматриваемого класса является их периодичность, т. е. повторяемость через определенные интервалы времени.

Движения, которые точно или приблизительно повторяются через одинаковые промежутки времени, называются механическими колебаниями.

Колебания бывают разные. Одни колебания, как, например, в швейной машине, способны совершаться только тогда, когда на тело действуют периодически изменяющиеся внешние силы, которые и вынуждают тело совершать колебательное движение. Такие колебания называют вынужденными. Другие же колебания обусловлены действием внутренних сил и потому способны происходить сами по себе. Таковы, например, колебания грузика на пружине, возникающие после того, как грузик сместили из положения равновесия и отпустили.

Колебания, происходящие под действием внутренних сил и возникающие в системе после того, как система была выведена из состояния равновесия и предоставлена самой себе, называются свободными.

К свободным колебаниям относятся: колебания груза на пружине, а также груза на нити (маятника).

Отличительной особенностью систем, в которых происходят свободные колебания, является наличие у них положения устойчивого равновесия. Именно около этих положений и совершаются свободные колебания.

Для того чтобы в той или иной системе возникли свободные колебания, необходимо выполнение следующих условий:

1. Системе должна быть сообщена избыточная энергия. Эту энергию можно сообщить системе либо в виде потенциальной энергии, либо в виде кинетической энергии, либо в виде и той и другой.

2. Избыточная энергия, сообщенная системе, не должна в процессе возникшего движения полностью тратиться на преодоление трения.

Эти два условия являются необходимыми, но не достаточными для существования свободных колебаний. Система, помимо этого, должна обладать еще некоторыми определенными свойствами, которые могут послужить причиной возникновения в системе колебаний.

Основные кинематические характеристики колебаний:

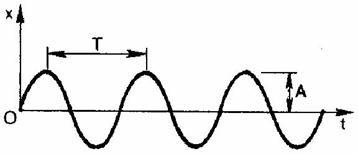
1) амплитуда колебаний (А)— это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда свободных колебаний определяется начальными условиями, измеряется амплитуда в метрах;

2) период колебания (Т)— это минимальный промежуток времени, по истечении которого система возвращается в прежнее состояние; иначе говоря, период колебания — это время, за которое совершается одно полное колебание;

3) частота колебаний (υ)— это число колебаний, совершаемых за 1 с, измеряется в герцах (Гц);

4) циклическая частота (w)— это величина, в 2π раз большая частоты.

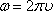
Физический смысл циклической частоты заключается в том, что она показывает, какое число колебаний совершается за 2π секунд. Измеряется циклическая частота в с^-1.

Для периода, частоты и циклической частоты справедлива формулы:

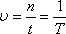
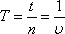
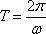
где п — число колебаний, а t — время, за которое произошло п колебаний.

В процессе свободных колебаний положение колеблющегося тела непрерывно изменяется. Если трение настолько мало, что им можно пренебречь, то графиком зависимости координаты колеблющегося тела (материальной точки) от времени является синусоидальная кривая, или, кратко, синусоида.

График зависимости координаты колеблющегося тела от времени называют графиком колебаний. По графику колебаний легко определяются все кинематические характеристики колебательного движения.

Колебания, при которых координата колеблющегося тела меняется с течением времени по закону синуса (или косинуса), называются гармоническими.

Если момент начала отсчета времени колебаний совпадает с моментом максимального отклонения маятника от положения равновесия, уравнение колебаний будет:

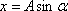или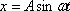

т. е. колебания будут синусоидальными и происходить без начальной фазы α₀х – смещение маятника.

Если момент начала отсчета времени колебаний не совпадает ни с моментом максимального отклонения от положения равновесия, ни с моментом прохождения им положения равновесия, то колебания происходят с начальной фазой и уравнение таких колебаний имеет вид:

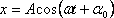или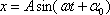

Фаза колебаний α – это величина, которая позволяет определить, какая доля периода прошла с момента начала колебаний и наиболее полно характеризует колебательный процесс:

Задачи механических колебаний можно условно разделить на четыре группы: задачи на уравнения гармонических колебаний, задачи о колебаниях пружинного маятника, задачи о колебаниях математического маятника и задачи о колебаниях физического маятника - маятника произвольной формы, к колебаниям которого нельзя применять формулы, применимые к колебаниям пружинного или математического маятников.

1. Свободные и вынужденные электромагнитные колебания

Электромагнитные колебания были открыты в известной мере случайно. После того как изобрели лейденскую банку (первый конденсатор) и научились сообщать ей большой заряд с помощью электростатической машины, начали изучать электрический заряд банки. Замыкая обкладки лейденской банки с помощью проволочной катушки, обнаружили, что стальные спицы внутри катушки намагничиваются. В этом ничего странного не было: электрический ток и должен намагничивать стальной сердечник катушки. Удивительным было то, что нельзя было предсказать, какой конец сердечника катушки окажется северным полюсом, а какой – южным. Повторяя опыт примерно в одних и тех же условиях, получали в одних случаях один результат, а в других – другой.

Далеко не сразу поняли, что при разрядке конденсатора через катушку возникает колебания. За время разрядки конденсатор успевает много раз перезарядиться, и ток меняет направление много раз. Из-за этого сердечник может намагничиваться различным образом.

Электромагнитные колебания – это колебания электрического заряда, силы тока, напряжения, связанные с ними колебания напряженности электрического поля и индукции магнитного поля, а также самостоятельные колебания в электромагнитной волне.

Обычно эти колебания происходят с очень большой частотой, значительно превышающей частоту механических колебаний. Поэтому для их наблюдения и исследования самым подходящим прибором является электронный осциллограф.

В электронно-лучевой трубке осциллографа узкий пучок электронов попадает на экран, способный светиться при бомбардировке его электронами. На горизонтально отклоняющие пластины трубки подается переменное напряжение развертки (пилообразной) формы. Сравнительно медленное напряжение нарастает, а потом очень резко уменьшается. Электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращается назад. После этого весь процесс повторяется. Если теперь присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране образуется временная «развертка» колебаний, подобная той которую вычерчивает маятник с карандашом на конце на движущемся листе бумаги. Колебания затухают с течением времени.

Эти колебания являются свободными. Свободными колебаниями называются колебания, возникающие под действием внутренних сил. По этому признаку колебания груза, подвешенного на пружине, или шарика на нити являются свободными колебаниями. Колебания под действием внешних периодически изменяющихся сил называются вынужденными колебаниями. Вынужденные колебания совершают поршень в цилиндре автомобильного двигателя и нож электробритвы, игла швейной машины и резец, строгального станка.

1. Волновые процессы. Звуковые волны.

2.1. Понятие волнового процесса

Волновым процессом называется любое изменение (возмущение) состояния сплошной среды, распространяющееся с конечной скоростью и несущее энергию.

Существует большое многообразие волновых процессов (типов волн): звуковые волны, сейсмические, волны на поверхности воды, волны механических колебаний в кристаллах, радиоволны, оптические волны. Во всех волновых процессах наблюдаются сходные закономерности поведения в пространстве и во времени, которые описываются одинаковыми математическими моделями и исследуются общими методами.

Выделим два основных типа волн: упругие и электромагнитные. Упругие (другое название акустические от греческого слова acustikos – слуховой) волны – это волны, связанные с колебаниями частиц при механической деформации упругой среды (жидкой, газообразной, твердой). При этом имеет место перенос энергии при отсутствии переноса вещества. В акустической волне частицы совершают колебания вокруг точки

покоя. Волна, у которой частицы среды совершают колебания вдоль направления распространения, называется продольной волной. Если частицы среды колеблются перпендикулярно направлению распространения волны, акустическая волна называется поперечной или сдвиговой. Среди упругих волн самые низкие частоты имеют инфразвуковые волны, лежащие ниже

границы слышимости их человеком (ниже 16 Гц). Слышимые звуковые колебания занимают диапазон частот от 16 Гц до 20 кГц. Волны более высоких частот – ультразвуковые (от 20 кГц до 1 ГГц) и гиперзвуковые (от 1 ГГц до 1000 ГГц).

Электромагнитные волны – это распространяющиеся в пространстве переменные во времени электромагнитные поля.

Электромагнитные волны всегда имеют поперечные к направлению распространения составляющие векторов напряженностей электрического и магнитного полей. Продольные составляющие этих векторов могут существовать лишь при определенных условиях (у границ раздела разных сред, вблизи возбуждающих источников, в линиях передачи). Чисто продольных электромагнитных волн не существует. Среди электромагнитных волн выделяют радиоволны с диапазоном частот от 3 ⋅103 Гц до 3 ⋅1011 Гц. Далее по частоте расположен оптический диапазон от 3 ⋅1011 Гц до 1, 5 ⋅10 Гц, включающий инфракрасное, видимое и ультрафиолетовое излучения. На более высоких частотах происходят рентгеновское и гамма – излучения.

Наука, занимающаяся изучением излучения, распространения и поглощения электромагнитных волн, называется электродинамикой. До диапазона инфракрасных волн все среды можно рассматривать как сплошные без учета их внутренней микроструктуры, волновыми процессами в таких средах занимается классическая электродинамика. На более высоких частотах следует учитывать микроструктуру среды и дискретность электромагнитного излучения (поток фотонов). В этом случае электромагнитное излучение описывается методами квантовой электродинамики.

Волновые процессы могут быть линейными и нелинейными. Волна называется линейной, если свойства среды для этой волны не зависят от интенсивности волны. Линейные волны распространяются независимо друг от друга без взаимных искажений. Пространство неограниченно может быть заполнено разными типами линейных волн, имеющих различные частоты и

направления распространения. Для линейных волн выполняется принцип суперпозиции (наложения) волн без взаимных искажений. Для линейных волн существует единый теоретический подход независимо от их природы. Нелинейная волна – это волна, под действием которой меняются свойства среды и соответственно меняются свойства самой волны. Это обычно происходит при большой интенсивности волны.

2.2. Гармоническая волна и ее параметры.

Гармоническая волна - волна, изменяющаяся во времени по гармоническому (синусоидальному) закону. Для этой волны также употребляется термин монохроматическая (одноцветная) волна, заимствованный из оптики. Любой волновой процесс можно представить с помощью преобразований Фурье через гармонические волны.

Кратко остановимся на основных определениях и понятиях гармонической волны. Уравнения плоской гармонической волны, распространяющейся, например, вдоль оси z в среде без потерь записывается в следующем виде

A( z , t ) = A₀ cos( ωt − kz + ϕ₀ ) . (1.1)

Под величиной A понимается физическая величина, определяющая волновой процесс. Максимальное значение этой величины называется амплитудой, обозначенной в (1.1) через A₀ . Размерность амплитуды определяется природой волнового процесса. Например, в звуковых волнах амплитуда измеряется в единицах давления паскалях (Па), в электромагнитных волнах амплитуда напряженности электрического поля измеряется в вольтах на метр (В/м), а магнитного поля - в амперах на метр (А/м).

Выражение, стоящее в скобках (1.1), называется фазой колебания, через которую определяется значение физической величины в данный момент времени и в данной точке пространства. Константа ϕ0 называется начальной фазой, использование которой имеет смысл при сравнении двух и более волн одной частоты в данной точке пространства и в фиксированный момент времени. Круговая частота ω связана с частотой f (число колебаний в единицу времени) соотношением

ω = 2 πf . (1.2)

Частота ω измеряется в радианах в секунду, частота f в герцах (1Гц – одно колебание в секунду). При известной частоте f период колебания находится из соотношения

T= 1/f (1.3)

Из периодичности волнового процесса в пространстве определяется длина волны.

Таким образом, длина волны – пространственный интервал, по прохождению которого фаза волны меняется на 2π вдоль направления распространения. Число длин волн, укладывающихся на расстоянии 2π метров, называется волновым числом и обозначается k.

Поверхность, на которой волновой процесс имеет одинаковую фазу колебания, называется поверхностью равных фаз или фронтом волны. По форме фронта волны можно выделить плоские, цилиндрические и сферические волны. Поверхность, на которой амплитуда волнового процесса постоянна, называется поверхностью равных амплитуд. Волна называется однородной, если у нее поверхности равных амплитуд и равных фаз совпадают, то есть на поверхности фронта не меняется амплитуда волнового процесса. В неоднородной волне амплитуда на поверхности фронта изменяется.

Плотность потока энергии (или интенсивность) волны – это энергия, переносимая волной через единицу перпендикулярно ориентированной поверхности за единицу времени. Плотность потока энергии пропорциональна квадратуре амплитуды.

Вектор плотности потока энергии в единицу времени (плотности потока мощности) принято называть вектором Умова-Пойнтинга.

Распространение волны происходит в направлении, перпендикулярном поверхности фронта волны. Плоская волна идет в одном направлении по нормали к ее фронту. Цилиндрическая волна расходится по радиусу в плоскости, перпендикулярной оси цилиндра. Сферическая волна расходится по радиусу перпендикулярно сферическому фронту. Элемент поверхности цилиндрического фронта возрастает прямо пропорционально расстоянию, при этом плотность потока мощности убывает обратно пропорционально расстоянию, а амплитуда цилиндрической волны убывает обратно пропорционально корню квадратному из расстояния. Элемент поверхности сферического фронта возрастает пропорционально квадрату расстояния, плотность потока мощности уменьшается обратно пропорционально квадрату расстояния, а амплитуда сферической волны убывает обратно пропорционально расстоянию. В среде с потерями распространяющиеся волны теряют часть своей энергии и их амплитуды убывают по экспоненциальному закону вдоль направления распространения.

2.3. Звуковые явления.

При распространении звуковой волны происходит затухание звука, связанное с различными необратимыми процессами. Часть энергии, которая переносится звуковыми волнами, поглощается средой.

Величина, равная отношению поглощённой звуковой энергии к звуковой энергии, поступающей в среду, называется коэффициен­том поглощения. Коэффициент поглощения зависит от внутреннего трения (вязкости) поглощающей среды и от её теплопроводности. Он так же зависит от скорости распростране­ния звука в этой среде, от плотности среды и частоты звуковой волны.

Звуковая волна, распространяясь в некоторой среде, когда-нибудь доходит до границы этой среды, за которой начинается другая среда, состоящая из других частиц, в которой и ско­рость звука другая. На такой границе происходит явление отражения звуковой волны. При этом сгущение частиц превраща­ется в разрежение, а разрежение - в сгущение.

Происходит это потому, что колебания, принесённые волной к границе, передаются частицами второй среды и они сами становятся источником новой звуковой волны. Эта вторич­ная волна распространяется не только во второй среде, но и в первой, откуда пришла первичная волна. Это и есть отраженная волна.

На границе двух сред происходит частичное поглощение и прохождение звука в другую среду. Доля отражённой энергии звуковой волны зависит в основном от соотношения плотностей этих сред и состояния поверхности раздела. Отражение звука, распространяющегося в воздухе, от твёрдого тела или жидкой поверхности происходит практически полностью. Звук, распро­страняющийся в плотной среде, также практически полностью отражается на границе раздела с воздухом.

Если преграда представляет собой более плотную среду, то при отражении происходит потеря полуволны. В большом помеще­нии после каждого звука возникает гул, который является результатом наложения звуковых волн, отраженных от различных преград в этом помещении. Например от стен, потолка, колонны и т.п.. Это явление называется реверберацией. Если в помеще­нии много отражающих поверхностей, особенно мягких, сильно поглощающих звук, то реверберация отсутствует. Явление ревер­берации учитывают в архитектуре, при проектировании больших залов, добиваясь определённой окраски звука, который приобре­тает мягкость и объёмность.

С явлением отражения звука связано такое известное явле­ние, как эхо. Оно состоит в том, что звук от источника дохо­дит до какого-то препятствия, которое и является границей двух сред, отражается от него, и возвращается к месту, где эта звуковая волна возникла. И если первичный звук и звук отражённый доходят до слушателя не одновременно, то он слышит звук дважды. Звук может испытать и несколько отражений. Тогда можно услышать звук много раз. Например раскаты грома.

При отражении звуковой волны от менее плотной среды, на­пример лёгкие газы, звуковая волна, распространяющаяся в воздухе, проходит через неё, вовлекая частицы этой среды в волновое движение и частично отражаясь.

Величина, равная отношению отражённого потока звуковой энергии к падающему потоку звуковой энергии, называется коэффициентом отражения. Величина, равная отношению проходя­щего потока звуковой энергии к падающему потоку звуковой энергии, называется коэффициентом пропускания.

Для звуковых волн выполняются законы отражения и прелом­ления, аналогичные законам отражения и преломления света.

2.4. Свойства звука.

Ощущение звука вызывается звуковыми волнами, достигающими органа слуха - уха. Важнейшая часть этого органа - барабанная перепонка. Пришедшая к ней звуковая волна вызывает вынужден­ные колебания барабанной перепонки с частотой колебаний в волне. Они воспринимаются мозгом как звук.

Звуки бывают разные. Мы легко различаем свист и дробь ба­рабана, мужской голос (бас) от женского (сопрано).

Об одних звуках говорят, что они низкого тона, другие мы называем звуками высокого тона. Ухо их легко различает. Звук, создаваемый большим барабаном, это звук низкого тона, свист - звук высокого тона. Простые измерения (развертка колебаний) показывают, что звуки низких тонов - это колебания малой частоты в звуковой волне. Звуку высокого тона соответствует большая частота колебаний. Частота колебаний в звуковой волне определяет тон звука.

Существуют особые источники звука, испускающие единствен­ную частоту, так называемый чистый тон. Это камертоны различ­ных размеров - простые устройства, представляющие собой изогнутые металлические стержни на ножках. Чем больше размеры камертона, тем ниже звук, который он испускает при ударе по нему.

Если взять несколько камертонов разного размера, то не представит труда расположить их на слух в порядке возрастания высоты звука. Тем самым они окажутся расположенными и по размеру: самый большой камертон даёт низкий звук, а маленький - наиболее высокий.

Звуки даже одного тона могут быть разной громкости. Гром­кость звука связана с энергией колебаний в источнике и в волне. Энергия же колебаний определяется амплитудой колеба­ний. Громкость, следовательно, зависит от амплитуды колеба­ний. Но связь между громкостью звука и амплитудой колебаний не простая.

Самый слабый ещё слышимый звук, дошедший до барабанной перепонки, приносит в 1 секунду энергию, равную примерно 10^-16 Дж, а самый громкий звук (звук реактивного ракетного двигателя в нескольких метрах от него) - около 10^-4 Дж. Следовательно, по мощности самый громкий звук примерно в тысячу миллиардов раз превосходит самый слабый.

Интенсивности звука при слуховом восприятии соответствует ощущение громкости звука. При определенной минимальной интен­сивности человеческое ухо не воспринимает звука. Эта мини­мальная интенсивность называется порогом слышимости. Порог слышимости имеет различные значения для различных частот. При больших интенсивностях ухо испытывает болевое ощущение. Наибольшая интенсивность при болевом восприятии звука называ­ется порогом болевого ощущения.

Уровень интенсивности звука определяется в децибелах (дБ). Например, громкость звука, шороха листьев оценивается в 10 дБ, шёпота - 20 дБ, уличного шума - 70 дБ. Шум громкостью 130 дБ ощущается кожей и вызывает ощущение боли.

Количество децибел равно десятичному логарифму отношения интенсивностей, умноженному на 10, т.е. 10 lg.(I/I0).

Обычно в акустике за I0 принимается интенсивность равная 1 пДж(м с), приблизительно равная интенсивности на пороге слышимости при 1000 Гц.

Простейшие наблюдения показывают, что громкость тона ка­кой-либо данной высоты определяется амплитудой колебаний. Звук камертона после удара по нему постепенно затихает. Это происходит вместе с затуханием колебаний, т.е. с уменьшением их амплитуды. Ударив камертон сильнее, т.е. сообщив колеба­ниям большую амплитуду, мы услышим более громкий звук, чем при слабом ударе. То же можно наблюдать и со струной, и вообще со всяким другим источником звука.

К таким же заключениям можно прийти, пользуясь не камер­тонами, а упрощённой сиреной - вращающимся диском с отвер­стиями, через которые продувается струя воздуха. Повышая напор струи воздуха, мы усиливаем колебания плотности воздуха позади отверстий. При этом звук, сохраняя одну и ту же вы­соту, делается громче. Ускоряя вращение диска, мы уменьшаем период прерываний воздушной струи. Вместе с тем звук, не меняясь по громкости, повышается. Можно также сделать в диске два или более рядов отверстий с разным количеством отверстий в каждом ряду. Продувание воздуха через каждый из рядов даёт тем более высокий звук, чем больше отверстий в этом ряду, т.е. чем короче период прерываний.

Но, взяв в качестве источника звука сирену, можно полу­чить хотя и периодическое, но уже негармоническое колебание: плотность воздуха в прерывистой струе меняется резкими толч­ками. На ряду с этим и звук сирены, хотя и является музыкаль­ным, но совсем не похож на тон камертона. Можно подобрать высоту звука сирены такой же, как и у какого-либо из камерто­нов. При этом и громкость звука можно сделать одинаковой. Тем не менее легко можно отличить звук камертона от звука сирены.

Таким образом, если колебание не является гармоническим, то на слух оно имеет ещё одно качество, кроме высоты и гром­кости, а именно - специфический оттенок, называемый тембром. По различному тембру мы легко распознаём звук голоса, свист, звучание струны рояля, скрипичной струны, звук флейты, гар­мони и т.д., хотя все эти звуки имели бы одну и ту же высоту и громкость. По тембру мы можем узнать голоса разных людей.

Исследование вопроса, с чем связан тембр звука, показало, что для нашего уха существенны только частоты и амплитуды тонов, входящих в состав звука, т.е. тембр звука определя­ется его гармоническим спектром. Сдвиги отдельных тонов по времени, другими словами, изменения фаз тонов, никак не воспринимаются на слух, хотя могут очень сильно менять форму результирующего колебания. Таким образом, один и тот же звук может восприниматься при очень различных формах колебания. Важно только, чтобы сохранялся спектр, т.е. частоты и ампли­туды составляющих тонов.

2.5. Скорость распространения звука.

В том, что распространение звуковых волн происходит не мгновенно, можно увидеть из простейших наблюдений. Если в дали происходит гроза, выстрел, взрыв, свисток паровоза, удар топором и т.п., то сначала все эти явления видно, а только потом, спустя некоторое время, слышен звук.

Как и всякая волна, звуковая волна характеризуется скоростью распространения колебаний в ней. Скорость распро­странения фазы волны в упругой среде жидкости или газа зави­сит от сжимаемости и плотности этой среды. В жидкостях и газах звук распространяется с постоянным давлением и его скорость пропорциональна корню квадратному из абсолютной температуры газа T. В сухом воздухе, содержащим 0,03 угле­рода, при температуре 0 ⁰C скорость звука равна 331,5 м/с, а с повышением температуры увеличивается:

____

 = T ,

где 1/273 - коэффициент расширения газа. В воде звук распространяется примерно в 4,25 раза быстрее, чем в воз­духе, а в твёрдых телах - ещё быстрее (около 5 10³ - 6 10³ м/с).

С длиной волны и частотой колебаний скорость звуко­вой волны связана формулой:

.

Скорость звука различна в разных средах. Например в водо­роде скорость распространения звуковых волн любой длины равна 1284 м/c, в резине - 1800 м/с, а в железе - 5850 м/c.

2.6. Эффект Доплера в акустике.

Частота звуковых колебаний, которые слышит неподвижный наблюдатель в случае, если источник звука приближается или удаляется от него, отлична от частоты звука, воспринимаемой наблюдателем, который движется вместе с этим источником звука, или и наблюдатель и источник звука стоят на месте. Изменение частоты звуковых колебаний (высоты звука), связанное с относительным движением источника и наблюдателя называется акустическим эффектом Доплера. Когда источник и приемник звука сближаются, то высота звука повышается, а если они удаляются. то высота звука понижается. Это связано с тем, что при движении источника звука относительно среды, в кото­рой распространяются звуковые волны, скорость такого движения векторно складывается со скоростью распространения звука.

Например, если машина с включенной сиреной приближается, а затем, проехав мимо, удаляется, то сначала слышен звук высокого тона, а затем низкого.