Комплект образцов презентаций индивидуальных итоговых проектов по математике обучающихся 9 классов

Великие математики древности

Проект ученицы 9 класса Г

Кочетковой Ольги

Руководитель проекта:

Мамасуева Татьяна Парфирьевна

Цель, задачи, актуальность

Цель: изучение биографии великих математиков и знакомство с самыми интересными фактами их жизни.

Задачи:

1.Узнать какие существовали математики в древности. 2.Узнать какие у них были самые интересные или самые известные труды.

Актуальность: мой проект полезен в первую очередь для учеников, потому что это интересно. Кроме того каждый человек должен знать великих людей в лицо, и знать почему их называют великими.

Содержание

1.Введение.

2.Аполлоний Пергский.

3.Аристотель.

4.Архимед.

5.Гиппарх.

6.Демокрит.

7.Пифагор.

8.Платон.

9.Фалес.

10.Эратосфен

11. Птолемей

12.Вывод

Аполлоний Пергский (262-190 гг. до н. э.)

Труды:

1.Труд о конических сечениях.

2.Отсечение отношения  в двух книгах, содержащих 180 теорем.

3.Отсечение площади в двух книгах, содержащих 124 теоремы.

4.Определенное сечение в двух книгах, содержащих 83 теоремы.

5.Вставки  в двух книгах, содержащих 125 теорем.

6.Касания  в двух книгах, содержащих 60 теорем.

Аристотель ( 384-322 гг. до н.э.)

Философские учения:

1.Учение о четырёх причинах.

2.Акт и потенция.

3.Категории философии.

4.Бог как перводвигатель, как абсолютное начало всех начал.

5.Идея души.

6.Космология Аристотеля.

7.Учение о государстве.

Архимед Сиракузский ( 287-212 гг. до н. э.)

1.Ввел в механику такое понятие, как центр тяжести .

2.Построил планетарий, где можно наблюдать движение пяти планет.

3.Архимед открыл полуправильные многогранники, которые теперь носят его имя.

Лучшим своим открытием он считал определение поверхности и объёма шара, поэтому на своей могиле он просил выбить шар, вписанный в цилиндр. Так, даже думая о смерти, он не может забыть о математике .

Гиппарх Никейский ( 190-120 гг. до н. э.)

Вклад в науку:

1.Гиппарх составил первый в Европе  звёздный каталог.

2. Открытие предварения равноденствий, или астрономической прецессии.

3.Гиппарх внёс существенный вклад в усовершенствование календаря.

4.Вычисление расстояний до Луны и Солнца и их размеров

Демокрит Абдерский ( 460-370 гг. до н. э.)

1.Демокрит развивает общеэллинское понятие меры, отмечая, что мера — это соответствие поведения человека его природным возможностям и способностям. 

2.Демокрит — сторонник концепции множественности миров.

Пифагор Самосский ( 570-490 гг. до н. э. )

Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов.

В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев».

Платон (между 429 и 427- 347 гг. до н. э.)

Учения Платона:

1.Диалектика Платона.

2.Политико-правовое учение Платона.

3.Учение о познании.

4.Учение о душе.

Фалес (640/624 — 548/ 545 до н. э. )

Считается, что Фалес «открыл» для греков созвездие Малой Медведицы как путеводный инструмент; ранее этим созвездием пользовались финикийцы.

Фалесу приписываются следующие положения:

1.Земля плавает в воде, а Солнце и другие небесные тела питаются испарениями этой воды.

2.Звезды состоят из земли, но при этом раскалены; Солнце — землистого состава [состоит из земли]; Луна — землистого состава [состоит из земли].

3.Земля находится в центре Вселенной; при уничтожении Земли рухнет весь мир.

Эратосфен Киренский ( 276-194 гг. до н. э.)

Достижения:

1.Эратосфен является основателем научной хронологии.

2.Эратосфену принадлежит термин «география» (землеописание).

3.Считается, что именно Эратосфен создал первую карту мира, которая давала примерное представление о взаимной удаленности городов и стран.

Клавдий Птолемей

Достижения:

1.Птолемей — автор трактата «Гармоника» в трёх книгах (окончание третьей книги не сохранилось), в котором развернул теорию звуковысотной системы 

2.Другой важный труд Птолемея середины II века нашей эры — Руководство по географии в восьми книгах представляет собой собрание знаний о географии всего известного античным народам мира

3.Теоремы о произведении диагоналей вписанного в круг четырёхугольника теорема Птолемея ,

Вывод

1.Мы узнали какие существовали великие математики.

2.Узнали их самые интересные (или самые знаменитые) открытия .

Источники информации

Аполлоний Пергский  //  Энциклопедический словарь Брокгауза и Ефрона  : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Джон Дж. О’Коннор  и  Эдмунд Ф. Робертсон .  Аполлоний Пергский  (англ.) — биография в архиве  MacTutor .

© 2019 Русская историческая библиотека

Мария Солопова.   Демокрит  // Энциклопедия « Кругосвет ».

Демокрит  / M. A. Солопова //  Новая философская энциклопедия  : в 4 т. / пред. науч.-ред. совета  В. С.  Стёпин . — 2-е изд., испр. и доп. — М. :  Мысль , 2010. — 2816 с.

Храмов Ю. А.  Демокрит // Физики: Биографический справочник / Под ред.  А. И. Ахиезера . — Изд. 2-е, испр. и дополн. — М.:  Наука , 1983. — С. 100. — 400 с. — 200 000 экз. (в пер.)

Пифагор в Викицитатнике

Пифагор на Викискладе

Ямвлих, О пифагоровой жизни

Диоген Лаэртский, Пифагор

Порфирий, Жизнь Пифагора

Бертран Рассел, История западной философии

Pythagoras of Samos (The MacTutor History of Mathematics archive)

Stanford Encyclopedia of Philosophy: Pythagoras

«Золотые стихи» пифагорейцев в Библиотеке Александра Кобринского

Бесонид, Пифагорово Слово

А.Охоцимский. Пифагор и пифагорейцы, число и огонь

Золотое сечение

Выполнила обучающаяся

9 г класса

Иволгина Полина Вячеславовна

Руководитель:

Мамасуева Татьяна Парфирьевна

Содержание

• 1) Актуальность проекта
• 2) История вопроса
• 3) Золотая спираль
• 4) Золотое сечение в живописи, фотографии, дизайне
• 5) Золотое сечение в искусстве. Архитектура
• 6) Золотое сечение и тело человека
• 7) Пропорция золотого сечения в природе
• 8) Вывод

Актуальность проекта

• Благодаря «Золотому сечению» было сделано множество открытий в науке, архитектуре, литературе, живописи, природе, анатомии и астрономии.
• В перечисленных областях знаний оно используется и в настоящее время.
• Вы узнаете какую роль играет эта пропорция в окружающем мире, как она связана с понятием гармонии и как и почему она используется в искусстве (живописи, архитектуре, фотографии…), дизайне и в остальных жизненных аспектах.

История

• Под золотым сечением понимается такое пропорциональное деление отрезка на неравные части, при котором длина всего отрезка так относится к его большей части, как длина большей части относится к длине меньшей. Это отношение равно иррациональному числу Ф=1.618…

,

Золотая спираль

• Что общего в расположении полипептидных цепей нуклеиновых кислот, лепестков розы, раковин моллюсков, рогов млекопитающих, подсолнуха, далеких космических галактик ?

Золотое сечение в живописи, фотографии, дизайне

• Основы композиции В живописи, фотографии, дизайне золотое сечение очень часто используется в виде классических приемов композиции (о чем вы можете прочитать, заглянув на любой сайт, посвященный этим видам искусства).

Золотое сечение в искусстве. Архитектура

• Золотое сечение пронизывает

всю историю искусства.

Пропорции тела человека и золотое сечение

• Идеальным, совершенным считается тело, пропорции которого составляет золотое сечение. Основные пропорции были определены Леонардо да Винчи, и художники стали сознательно их использовать.

Пропорции золотого сечения в природе

• Форма птичьих яиц описывается золотым сечением.

• Совершенная форма тела стрекозы создана по законам золотого сечения: отношение длины хвоста и корпуса равно отношению общей длины к длине хвоста.

Вывод

• Золотое сечение – это один из основных принципов природы.
• Человеческое представление о красивом сформировалось под влиянием того – какую гармонию и порядок видит он сам в природе.

Литература

• https://ru.wikipedia.org/wiki/ Золотое_сечение
• Савин А.   Число Фидия - золотое сечение  (рус.) // "Квант" : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
•   Прохоров А. Золотая спираль, Квант, 1984, №9
• http://bapachi.by/zolotoe-sechenie-v-prirode-cheloveke-iskusstve/

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №59» Проект по математике «История возникновения чисел»

Выполнил обучающейся 9 Г класса Шульгин Илья Дмитриевич Руководитель: Мамасуева Татьяна Парфирьевна

Цель работы

• Выяснить как появились числа
• Как они развивались в разных народах и культурах
• Разобраться как числа стали такими какими мы видим их сейчас
• Узнать значение чисел и их мифический смысл
• Сделать вывод по работе

История возникновения чисел

У древних людей, кроме каменного топора и шкуры вместо одежды, ничего не было, поэтому считать им было нечего. Постепенно они стали приручать скот, возделывать поля; появилась торговля, и тут уж без счёта никак не обойтись. Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги.

Системы счисления

От пальцевого счёта пошли пятеричная система счисления (одна рука), десятеричная (две руки), двадцатеричная (пальцы рук и ног). В древние времена не существовало единой для всех стран системы счёта. Некоторые системы исчисления брали за основу 12, другие – 60, третьи – 20, 2, 5, 8 .

Числа по-шумерски

Первыми придумали запись чисел древние шумеры. Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом обжигали. Вот так выглядели эти дощечки.

Шумерская система счисления

Шестидесятери́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 60. Изобретена шумерами в III тысячелетии до н. э., использовалась в древние времена на Ближнем Востоке.

Вавилонские числа

Вавилонская система счисления применялась за две тысячи лет до н. э. Для записи чисел использовались всего два знака: стоячий клин для обозначения единиц и лежачий клин для обозначения десятков внутри шестидесятеричного разряда.

Числа египтян

Древние египтяне на очень длинных и дорогих папирусах писали вместо цифр очень сложные и огромные знаки. Вот так, например, выглядели некоторые из египетских цифр.

Числа египтян

Так же египтяне пользовались дробями. Для трех дробей существовали специальные знаки. Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху.

Числа египтян

Все правильные дроби записывались как сумма таких дробей.

Числа индейцев майя

Цифры майя основаны на двадцатеричной позиционной системе счисления, использовавшиеся цивилизацией Майя в доколумбовой Месоамерике. Эта система использовалась для календарных расчётов. В быту майя использовали аддитивную непозиционную систему, сходную с древнеегипетской. Об этой системе дают представление сами цифры майя, которые являются записью первых 19 натуральных чисел в пятеричной непозиционной системе счисления. Аналогичный принцип составных цифр использован в древнейшей известной шестидесятеричной позиционной системе счисления и древнекитайской десятичной позиционной системе для расчётов на счётной доске.

Числа индейцев майя

Цифры майя состояли из нуля, который обозначался пустой ракушкой, и 19 составных цифр. Эти цифры конструировались из знака единицы (точка) и знака пятёрки (горизонтальная черта). Например, цифра, обозначающая число 19, писалась как четыре точки в горизонтальном ряду над тремя горизонтальными линиями. Сходство конструкции цифр Майя с древнеегипетскими, римскими и древнекитайскими цифрами обусловлено тем, что первоначально расчёты не велись на бумаге. Цифры выкладывались на ровной поверхности специальными палочками. Майя использовали также пустую ракушку и, вероятно, камешки или косточки плодов.

Числа индейцев майя

Числа свыше 19 писались согласно позиционному принципу снизу вверх по степеням 20. Например:

32 писалось как (1)(12) = 1 × 20 + 12

429 как (1)(1)(9) = 1 × 400 + 1 × 20 + 9

4805 как (12)(0)(5) = 12 × 400 + 0 × 20 + 5

Третий разряд (четырёхсотки)

Второй разряд (двадцатки)

Первый разряд (единицы)

32

429

4805

Числа индейцев майя

Для записи цифр от 1 до 19 иногда также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах.

Римская система счисления и их числа

Десятичную систему счисления ввели римляне. Римские цифры до сих пор используют в часах и для оглавления книг, а также и во многих школах, но уже не для счёта. В некоторых случаях с очень большими числами над римскими числами ставили черту. Черта сверху могла обозначать увеличение значения цифры в 1000 раз: V с чертой сверху = 5000 .

Римская система счисления и их числа

Но такая система цифр тоже была слишком сложной для счёта. Так как занимала очень много места.

Числа народов Азии

Индейцы и народы Древней Азии при счёте завязывали узелки на шнурках разной длинны и цвета. У некоторых богатеев скапливалось по несколько метров этой верёвочной «счётной книги», попробуйте, вспомнить через год, что означают четыре узелка на красном шнурке! Поэтому того, кто завязывал узелки, называли вспоминателем.

Греческая система счисления

1 α 10 ι 100 ρ

2 β 20 κ 200 σ

3 γ 30 λ 300 τ

4 δ 40 μ 400 υ

5 ε 50 ν 500 φ

6 ϝ 60 ξ 600 χ

(или ϛ)

7 ζ 70 ο 700 ψ

8 η 80 π 800 ω

9 θ 90 ϟ 900 ϡ

Греческая система счисления, также известная как ионийская или новогреческая — непозиционная система счисления. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϛ , ϟ и ϡ . Эта система пришла на смену аттической, или старо греческой, системе, которая господствовала в Греции в III веке до н. э. Необходимость сохранять порядок букв ради сохранения их числовых значений привела к относительно ранней (IV век до н. э.) стабилизации греческого алфавита.

Славянские числа

Предки нашего народа, русского – славяне для обозначения чисел употребляли буквы. Этот способ обозначения цифр называется цифирью. Но у наших предков славян буквы не только обозначали цифры, но и каждая буква имела свой смысл.

Славянские числа

Так же для обозначения больших чисел славяне придумали свой оригинальный способ, к примеру: десять тысяч – тьма, десять тем – легион, десять легионов – леорд, десять леордов – ворон, десять воронов – колода. Но Петру Великому это казалось очень неудобным (хотя я бы с ним и поспорил), и он ввёл привычные для всех нас десять цифр, которые мы используем и по сей день .

Древнекитайские цифры

Цифры Сучжоу — единственная отчасти сохранившаяся система, основанная на счёте палочками. Эта система сформировалась на базе более древней системы цифр, которые выкладывались палочками для вычислений на счётной доске, использовавшейся в Южной Сун. Долгое время расчёты велись почти только на счётной доске. На бумаге записывался результат. Сучжоуские цифры использовались в качестве скорописи в коммерции, бухгалтерии.

Древнекитайские цифры

В официальных документах использовались «формальные» китайские цифры, их сложнее перепутать при записи и чтении. В России на финансовых документах аналогичную функцию выполняет графа «сумма прописью». Цифры Сучжоу были популярны на рынках, в Гонконге они дожили до начала 1990-х, но постепенно вытесняются арабскими цифрами. Сегодня цифры Сучжоу используются только на некоторых рынках для записи цен.

Индо-арабские числа

Как принято считать числа которыми мы пишем в наши дни арабские но на самом деле они индо-арабские и придумали их в индии в 1 веке нашей эры. И выглядели они так.

Арабские или индо-арабские числа

«Современные цифры» — обычные арабские цифры. «Арабские цифры» — индо-арабские и персидские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — индо-арабский, справа — персидский. «Индийские цифры» — цифры деванагари современной Индии.

Арабские числа

Арабские или современные числа всем кажутся обыденными, но что если я скажу, что их можно считать с помощью углов. Так посчитав углы, можно даже незнающему человеку понять что перед ним, за число.

Арабские числа

Но со временем углы сгладились, и цифры приобрели привычный нам вид. Вот уже много столетий весь мир пользуется арабской системой записи чисел. Этими десятью значками можно легко выразить огромные значения.

Значение чисел в современном мире

Сейчас цифры и числа имеют огромную роль в нашей жизни! Так они используются: в работе с компьютером, для оплаты товаров и услуг мы считаем сколько денег нам требуется, для оплаты налогов, и многого, многого другого!

Значение чисел в современном мире

И если вы считаете что числа в жизни вам не пригодятся, то вы глубоко заблуждаетесь! Они играют возможно лидирующую роль в современной жизни и в современном обществе, и без них никак. И из-за роста технологий значение чисел всё растёт, а они сами начинают править миром!

«Главное число» человека

Древние учёные считали, что цифры имеют таинственный, магический смысл и влияют на человека. По верованиям древних, у каждого человека есть некое число, обладающее мистической силой, влияют на характер и привычки. В нумерологии, науке о числах, используют первые 9 чисел от 1 до 9.

Значение чисел по Пифагору

Пифагор, его ученики и последователи сократили все числа до цифр от 1 до 9 включительно, так как они являются исходными числами, из которых могут быть получены все другие. Знаменитый Корнелиус Агриппа в своём труде «Оккультная философия», вышедшем в 1533 году, назвал эти числа и их значения.

Значение чисел по Пифагору

Число 1 – число цели, которое проявляется в форме агрессивности и амбиции.

Число 2 – число с крайностями. Оно поддерживает равновесие, смешивая позитивные и негативные качества.

Число 3 – означает неустойчивость. Оно объединяет талант и весёлость и символизирует приспособляемость.

Значение чисел по Пифагору

Число 4 – число означает - устойчивость и прочность.

Число 5 – символизирует риск. Это число является и самым счастливым, и самым непредсказуемым.

Число 6 – символ надёжности. Оно находится в гармонии с природой. Это идеальное число.

Значение чисел по Пифагору

Число 7 – число символизирует тайну, а так же изучение и знание.

Число 8 – число материального успеха. Оно означает надёжность, доведённую до совершенства, равновесие.

Число 9 – символ всеобщего успеха. Оно объединяет черты целой группы.

Интересные факты про числа

1. В таких странах, как Китай, Япония и Корея число «4» считается несчастливым. Поэтому этажи с номерами, которые заканчиваются на «4» отсутствуют.

Интересные факты про числа

2. Центильон – это самое большое число, которое выглядит как 1 с 600 нулями. Это число было записано еще в 1852 году.

Интересные факты про числа

3. Число «13» - во многих государствах также считается неудачным. Поэтому этаж после «12» имеет обозначение «14», «12А» или «М» (тринадцатая буква в алфавите).

Интересные факты про числа

4. Арабы записывают цифры справа налево, начиная с младших разрядов. Поэтому увидев знакомые нам арабские цифры в тексте арабских народов, мы прочитаем их слева направо неправильно.

Интересные факты про числа

5. Интересные факты о числах касаются и современных технологий. Так, Google – одна из самых популярных поисковых систем. Ее придумали Сергей Брин и Ларри Пейдж. Название поисковой системы было выбрано неспроста. Так, ее создатели захотели показать то количество информации, которую система может обработать. В математике число, которое состоит из единицы и ста нулей называется «гугол». Интересно и то, что название «Google» записано неправильно (не «googol»). Но такая идея названия основателям понравилась еще больше.

Интересные факты про числа

6. 666 – это сумма всех чисел на рулетке казино.

Интересные факты про числа

7. Число «13» в Греции считается несчастливым днем только тогда, когда выпадает во вторник. В Италии опасаются пятницы 17-го. А вот статисты Нидерландов подсчитали, что именно 13-го числа случается меньше аварий и несчастных случаев, поскольку люди более осторожны и собраны.

Интересные факты про числа

8. Термин «цифра» в переводе с арабского означает «ноль». Только со временем данное слово начали использовать для обозначения любого численного символа.

Интересные факты про числа

9. Число «7» считается самым счастливым числом.

Интересные факты про числа

10. У сороконожек совсем не 40 ножек, их может быть от 30 до 400.

Вывод

Проведя это исследование я могу сказать что многие народы не зависимо друг от дуга придумали числа. Это происходило в разных точках света и в разные периоды времени но у многих никогда не встречавшихся народов очень похожие числа и системы счисления к примеру у славян и греков были алфавитные цифры а у римлян китайцев и майя были очень похожие числа записываемые с помощью палочек или чёрточек.

Вывод

И вот мы можем увидеть что всё время числа и их запись старались усовершенствовать но они до сих пор не совершенны.

Спасибо за внимание!

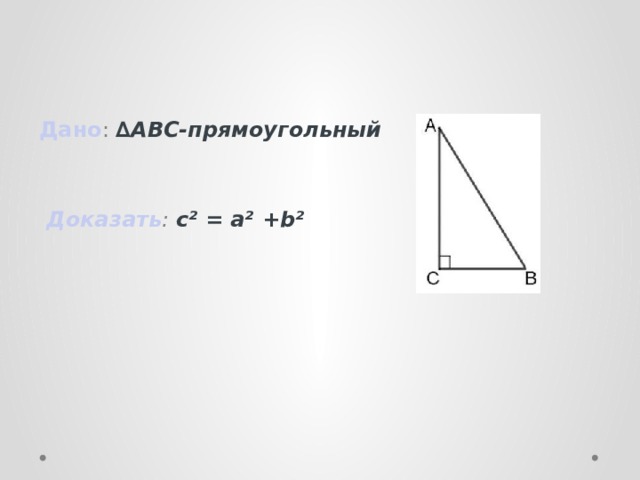
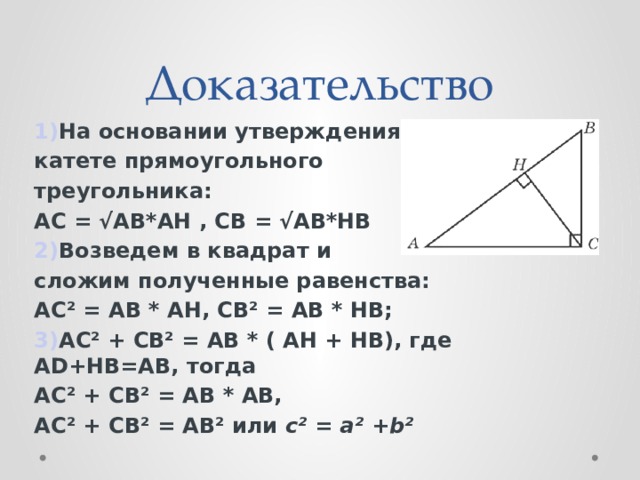
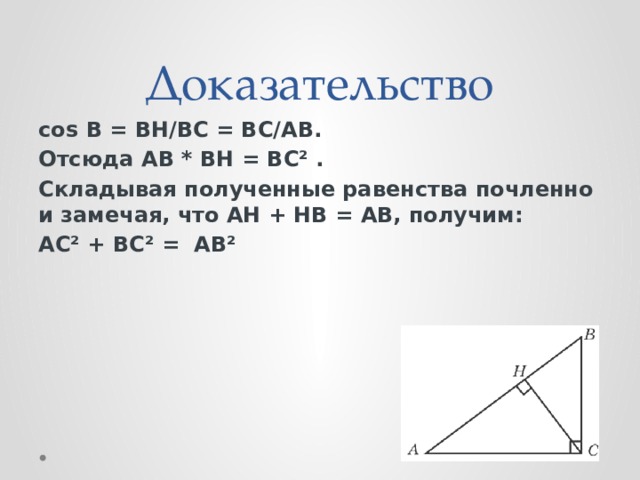
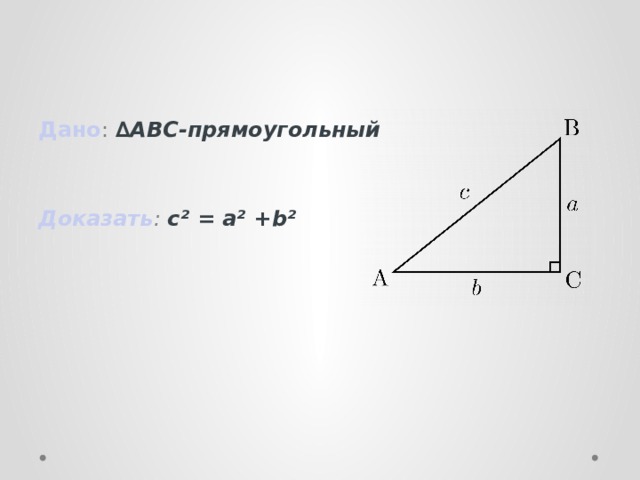
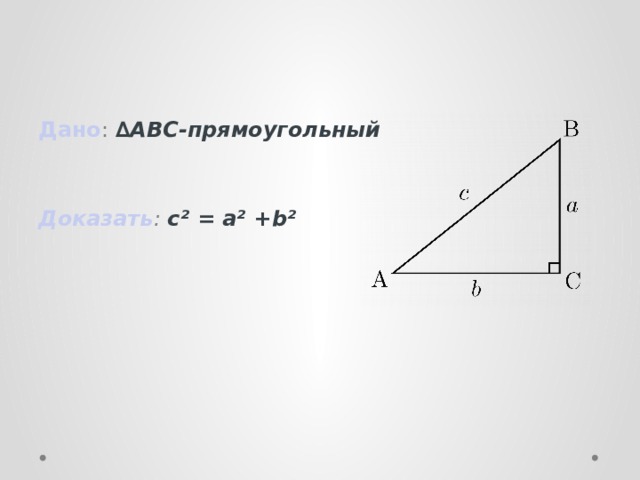
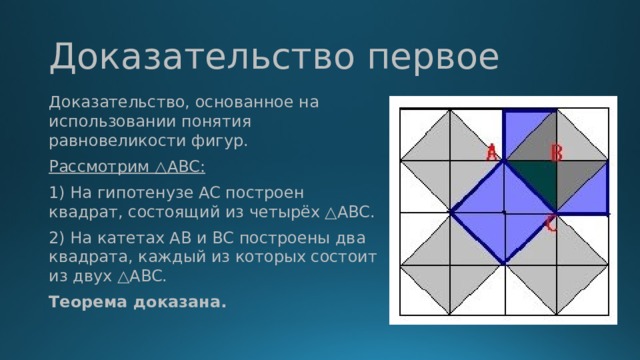
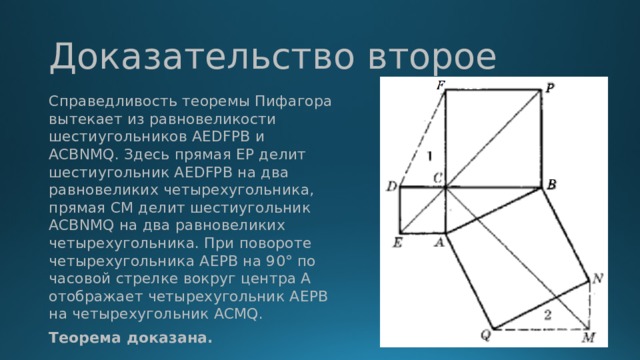
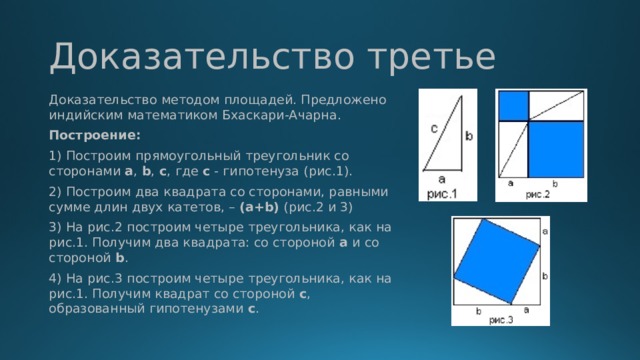
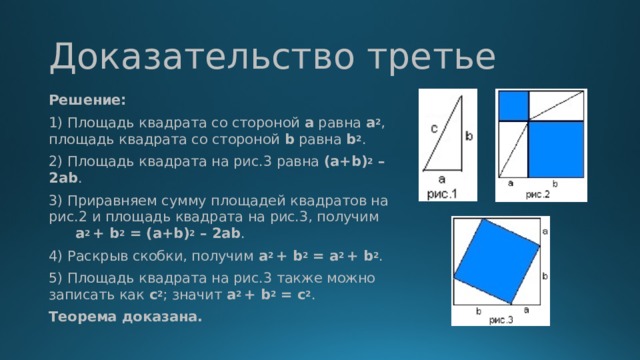
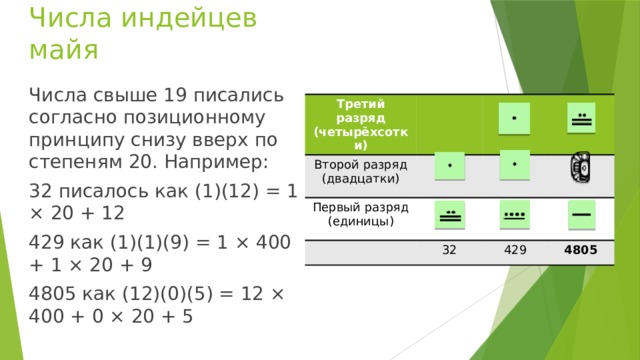
тема

“ Решение квадратных уравнений”

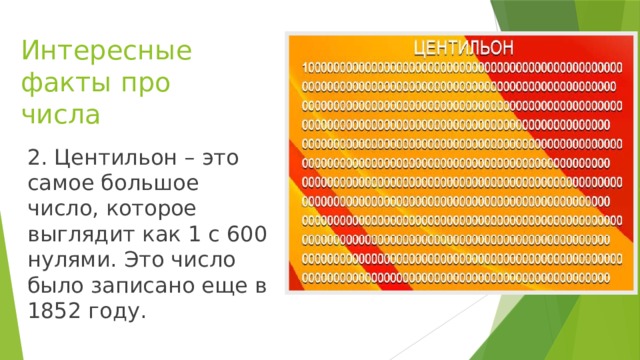
Выполнил: Оганян Егор 9Д Преподаватель: Мамасуева Татьяна Порфирьевна

Содержание.

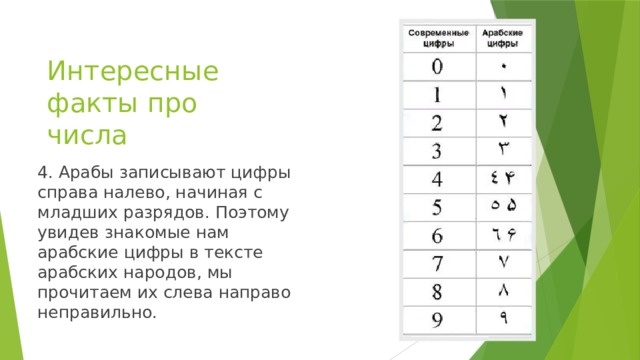
1. Содержание

2. Цели.

3. Задачи

3.1 Основополагающий вопрос;

3.2 Проблемные вопросы;

3.3 Учебные вопросы.

• Теоретический материал.

Цели :

Знакомство с различными способами решения квадратных уравнений

Задачи

Основополагающий вопрос:

Решение квадратных уравнений.

Проблемные вопросы: Какими способами можно решать квадратные уравнения?

Учебные вопросы:

1. Что такое квадратное уравнение?

2. Какие существуют виды квадратных уравнений?

3. Что называется дискриминантом квадратного уравнения?

4. От чего зависит количество корней квадратного уравнения?

5. Каковы формулы для нахождения корней квадратного уравнения?

6. Как формулируется теорема Виета?

Определение квадратного уравнения, его виды.

Квадратным уравнением называется уравнение вида

ax 2 + bx + c = 0,

где х - переменная , а,b и с -некоторые числа, причем, а ≠ 0.

Если в квадратном уравнении ах 2 + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением . Неполные квадратные уравнения бывают трёх видов:

1) ах 2 + с = 0, где с ≠ 0;

2) ах 2 + bх = 0, где b ≠ 0;

3) ах 2 = 0.

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент a :

х 2 +px + q = 0

Различные способы решения квадратных уравнений.

1) Разложение левой части уравнения на множители.

Решим уравнение х 2 + 10х – 24 = 0.

Разложим левую часть уравнения на множители:

х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х – 2) = 0.

Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. это означает, что числа 2 и – 12 являются корнями уравнения х 2 + 10х – 24 = 0.

2) Метод выделения полного квадрата

Решим уравнение х 2 + 6х – 7 = 0

Выделим в левой части полный квадрат. Для этого запишем выражение

х 2 + 6х в следующем виде: х 2 + 6х = х 2 + 2· х ·3.

В полученном выражении первое слагаемое – квадрат числа х , а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 3 2 , так как

х 2 + 2· х ·3 + 3 2 = (х + 3) 2 .

Преобразуем теперь левую часть уравнения

х 2 + 6х – 7 = 0,

прибавляя к ней и вычитая 3 2. Имеем:

х 2 + 6х – 7 = х 2 + 2· х ·3 + 3 2 – 3 2 – 7 = (х + 3) 2 – 9 – 7 = (х + 3) 2 – 16.

Таким образом, данное уравнение можно записать так:

(х + 3) 2 –16 = 0, т.е. (х + 3) 2 = 16.

Следовательно, х + 3 = 4, х 1 = 1, или х +3 = - 4 , х 2 = – 7.

Решение неполных квадратных уравнений.

1. Если ах 2 = 0. Уравнения такого вида решаются по алгоритму:

1) найти х 2 ;

2) найти х.

Например, 5х 2 = 0 . Разделив обе части уравнения на 5 получается:

х 2 = 0, откуда х = 0.

2. Если ах 2 + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:

1) перенести слагаемые в правую часть;

2) найти все числа, квадраты которых равны числу с.

Например, х 2 - 5 = 0, х 2 = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два -

и

x 2 = минус корень из пяти

Таким образом, уравнение х 2 - 5 = 0 имеет два корня: x 1 = корень из 5,

и других корней не имеет.

3. Если ах 2 + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:

1) вынести общий множитель за скобки;

2) найти x 1 , x 2 .

Например, х 2 - 3х = 0. Перепишем уравнение х 2 – 3х = 0 в виде

х ( х – 3 ) = 0. Это уравнение имеет, очевидно, корни x 1 = 0, x 2 = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х

( х – 3 ) = 0 получится число, не равное нулю.

0, т.е. В случае, когда - = m , - где m0, уравнение х 2 = m имеет два корня = = - Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня." width="640"

Вывод:

1) если уравнение имеет вид ах 2 = 0, то оно имеет один корень х = 0;

2) если уравнение имеет вид ах 2 + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x 1 = 0; x 2 = - ;

3) если уравнение имеет вид ах 2 + с = 0, то его преобразуют к виду

ах 2 = - с и далее х 2 = -

-

В случае, когда

0,уравнение х 2 =

не имеет корней (значит, не имеет корней и исходное уравнение

ах 2 +с=0).

0, т.е.

В случае, когда -

= m ,

-

где m0, уравнение х 2 = m имеет два корня

=

= -

Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.

0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня, которые находятся по формулам: (1) ; Например, 3х 2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b 2 – 4ас = 8 2 – 4*3*(-11) = 64 + 132 = 196. Так как D 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:" width="640"

Решение полных квадратных уравнений

ах 2 + bx + c = 0, где a,b,c – заданные числа, а ≠ 0, х – неизвестное.

Рассмотриваются следующие случаи решения полных квадратных уравнений: D 0.

1. Если D

Например, 2х 2 + 4х + 7 = 0.

Решение: здесь а = 2, b = 4, с = 7.

D = b 2 – 4ас = 4 2 – 4*2*7 = 16 – 56 = - 40.

Так как D

2. Если D = 0, то квадратное уравнение ах 2 + bx + c = 0 имеет один корень, который находится по формуле

Например, 4х – 20х + 25 = 0. Решение: а = 4, b = - 20, с = 25.

D = b 2 – 4ас = (-20) 2 – 4*4*25 = 400 – 400 = 0.

Так как D = 0, то данное уравнение имеет один корень. Этот корень находится по формуле

3. Если D 0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня, которые находятся по формулам:

(1)

;

Например, 3х 2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b 2 – 4ас = 8 2 – 4*3*(-11) = 64 + 132 = 196.

Так как D 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:

0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня ;" width="640"

.

Вывод:

Если D

Если D = 0, то квадратное уравнение имеет один корень,

который находится по формуле

Если D 0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня

;

0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p . Если p0 , то оба корня отрицательные, если p , то оба корня положительны. б) Если свободный член q приведенного квадратного уравнения отрицателен ( q то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p0." width="640"

Решение приведенных квадратных уравнений

Теорема Виета . Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

x 1 + x 2 = - p,

x 1 x 2 = q.

Иначе говоря, если x 1 и x 2 - корни уравнения х 2 +px + q = 0, то

Теорема, обратная теореме Виета . Если для чисел x 1 , x 2, p, q справедливы формулы то x 1 и x 2 - корни уравнения х 2 +px + q = 0 .

а) Если свободный член q

приведенного квадратного уравнения положителен ( q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p .

Если p0 , то оба корня отрицательные, если p , то оба корня положительны.

б) Если свободный член q

приведенного квадратного уравнения отрицателен ( q то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p0.

Свойства коэффициентов квадратного уравнения .

Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.

1.Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю),

то х 1 = 1, х 2 =

Решим уравнение 345х 2 – 137х – 208 = 0.

Решение . Так как а + b + с = 0 (345 – 137 – 208 = 0), то х 1 = 1, х 2 =

Ответ : 1; –

2. Если а - b + с = 0, или b = а + с, то х 1 = – 1, х 2 = –

Решим уравнение 132х 2 + 247х + 115 = 0

Решение. Т. к. а-b+с = 0 (132 – 247 +115=0), то

х 1 = - 1, х 2 = -

Ответ: - 1; -

Графическое решение квадратного уравнения

Если в уравнении x 2 + px + q = 0

перенести второй и третий члены в правую часть, то получим

x 2 = – px – q .

Построим графики зависимостей у = х 2 и у = – px – q .

График первой зависимости – парабола , проходящая через начало координат.

График второй зависимости – прямая .

Возможны следующие случаи: прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;

- прямая и парабола могут касаться (только одна общая точка),т.е. уравнение имеет одно решение;

- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

Решим графически уравнение х 2 – 3х – 4 = 0.

Решение. Запишем уравнение в виде

х 2 = 3х + 4

Построим параболу у = х 2 и прямую у = 3х + 4.

Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).

Прямая и парабола пересекаются в двух точках А и B с абсциссами х 1 = – 1 и

х 2 = 4.

В

А

Решение квадратных уравнений с помощью номограммы.

Это старый и незаслуженно забытый способ решения квадратных уравнений.

Номограмма для решения уравнения z 2 + pz+ q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам:

ОВ =

, АВ =

Полагая ОС = р, ЕD = q, ОЕ = а , из подобия треугольников САН и СDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0,

причем буква z означает метку любой точки криволинейной шкалы.

1. Для уравнения

z 2 – 9z + 8 = 0.

Номограмма дает корни

z 1 = 8, 0 и z 2 = 1, 0 (рис. 12).

2. Решим с помощью

номограммы уравнение 2z 2 – 9 z + 2 = 0.

Разделим коэффициенты этого

уравнения на 2,получим уравнение

z 2 – 4, 5 + 1 = 0.

Номограмма дает корни z 1 = 4 и z 2 = 0,5.

Спасибо за внимание