Просмотр содержимого документа
«Конспект лекции " Динамика вращательного движения"»
Динамика вращательного движения
Момент инерции. Теорема Штейнера.
Момент импульса.
Момент силы.
Кинетическая энергия вращающегося тела
Аналогия динамики поступательного и вращательного движений.
Момент инерции. Теорема Штейнера
При вращательном движении инертность тел зависит не только от массы тела, но и от распределения этой массы относительно оси вращения. Величина, учитывающая оба обстоятельства, называется моментом инерции тела.
Момент инерции J, (кг·м2) – мера инертности тела при вращательном движении. 
О Момент инерции материальной точки:
m r
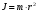 . (1)
. (1)
O'
Момент инерции твёрдого тела:
O 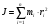 . (2)
. (2)
r1 m1
m2 r2
r3 m3
Для сплошного тела  и
и 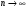 :
:
O'  . (3)
. (3)
Формула (3) позволяет рассчитать момент инерции любого тела.
В качестве примера вычислим момент инерции цилиндра (диска) относительно его геометрической оси: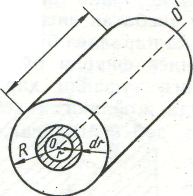
 ;
;  ,
,
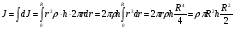 ;
;

 ,
, 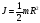 .
.
![]()
O Момент инерции кольца: 
m R
![]()
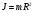 .
.
![]() O'
O'
O Момент инерции шара:
 R
R  .
.
O
Момент инерции стержня:
 .
.
 O'
O'
Момент инерции относительно любой оси определяется по теореме Штейнера : момент инерции тела относительно любой оси есть сумма момента инерции тела относительно параллельной оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
 O C
O C  . (4)
. (4)
O' C'
d
В качестве примера определим момент инерции стержня относительно оси AA':
O A  ;
;
![]()

 .
.
d=
O' A'
Векторное произведение векторов  и
и  :
:  .
.
Модуль вектора  равен:
равен:  ,
,  .
. 

Направление вектора  определяется правилом буравчика.
определяется правилом буравчика. 
 α
α
Момент импульса
 Момент импульса
Момент импульса  - мера вращательного движения тела.
- мера вращательного движения тела.  . (5)
. (5)
|   O 
 α α m | Момент импульса материальной точки относительно точки О равен векторному произведению радиус-вектора материальной точки на её импульс:  ; ;  . .
|
Момент импульса материальной точки относительно оси OO`:
![]() О
О


 ,
,  .
.
900


![]()
 m
m
O'
Момент импульса твёрдого тела относительно оси:  .
.
Т.к. угловая скорость каждой точки твёрдого тела одинакова:  , то
, то  .
.
Поэтому:  .
.
 Учитывая формула (2), получим:
Учитывая формула (2), получим:  .
.  . (5)
. (5)
Момент силы
Момент силы  , (Н·м) – мера взаимодействия тела при вращательном движении.
, (Н·м) – мера взаимодействия тела при вращательном движении.
 Момент силы относительно точки О
Момент силы относительно точки О 

 равен векторному произведению радиус-
равен векторному произведению радиус-
 вектора точки приложения силы на силу:
вектора точки приложения силы на силу:

 α
α  . (6)
. (6)
 ; [M]= Н·м.
; [M]= Н·м.
 - плечо силы, - наименьшее расстояние от точки О до направления действия силы.
- плечо силы, - наименьшее расстояние от точки О до направления действия силы.
Вращающееся тело, как всякое движущееся тело, обладает кинетической энергией.
Кинетическая энергия вращающегося тела
Кинетическая энергия вращающегося тела – равна сумме кинетических энергий всех частиц тела:

.
 . (7)
. (7)
Работа при вращательном движении:
 ;
;  ;
;  ;
;

 . (8)
. (8)
Работа затрачивается на увеличение кинетической энергии тела:
 .
.

 ;
;  ;
;  ;
;

![]()

 ;
;


 .
.  .
.

![]()
 (9) основной закон динамики
(9) основной закон динамики

 (10) вращательного движения.
(10) вращательного движения.
Аналогия динамики поступательного и вращательного движений
| ДВИЖЕНИЕ |
| ПОСТУПАТЕЛЬНОЕ | ВРАЩАТЕЛЬНОЕ |
| Мера инертности |
| Масса m | Момент инерции J |
| Мера механического движения |
| Импульс  | Момент импульса  |
| Мера взаимодействия |
| Сила  | Момент силы  |
| Импульс силы  | Момент импульс силы  |
| Основной закон динамики |
| 
| 
|
| 
| 
|
| Кинетическая энергия |
| 
| 
|
| Работа |
| 
| 
|
| Мощность |
| 
| 
|








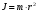 . (1)
. (1)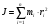 . (2)
. (2)
 и
и 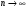 :
: . (3)
. (3)
 ;
;  ,
,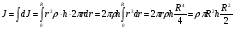 ;
;
 ,
, 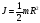 .
.
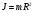 .
. R
R  .
.
 .
.
 O'
O' 









