Общие понятия теории множеств
Множество — одно из основных понятий современной математики, с которым каждый человек знаком со школьной скамьи. «Множество решений уравнения или неравенства», «множество точек на плоскости», «множество действительных чисел» и т.д. — привычные словосочетания, не требующие дополнительных рассуждений и определений.
Понятия множество, элементы множества — первичные базисные неопределяемые понятия, на которых строится теория множеств.
Совокупность элементов, объединенных некоторым признаком, свойством, составляет понятие множество.
Например, множество книг в библиотеке, множество студентов в группе, множество натуральных чисел N и т.д.
Запись 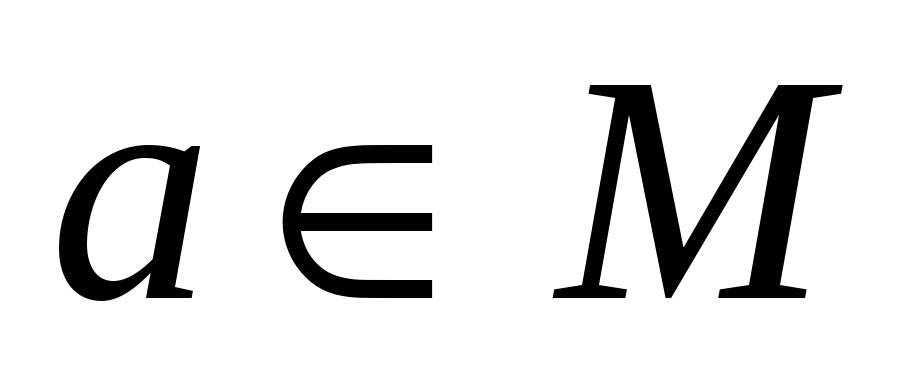 означает: элемент а принадлежит множеству М, т.е. элемент а обладает некоторым признаком. Аналогично
означает: элемент а принадлежит множеству М, т.е. элемент а обладает некоторым признаком. Аналогично  читаем как: элемент а не принадлежит множеству М.
читаем как: элемент а не принадлежит множеству М.
Множество считается заданным, если или перечислены все его элементы, или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству. Первый вариант будем записывать так: М = {ть т2,..., тк }. Например, М={0,1). Последний вариант будем записывать так: М={b | P(b)}. Такая запись читается как: М состоит из тех (всех) элементов b, которые обладают признаком Р. Например, М= {п| , п 5} означает: М составляют только те натуральные числа, которые меньше пяти. Само свойство Р будем называть характеристическим. В качестве характеристического свойства может выступать указанная для этого свойства порождающая процедура, которая описывает способ получения элементов нового множества из уже полученных элементов или из других объектов. Тогда элементами множества считаются все объекты, которые могут быть получены с помощью этой процедуры.
, п 5} означает: М составляют только те натуральные числа, которые меньше пяти. Само свойство Р будем называть характеристическим. В качестве характеристического свойства может выступать указанная для этого свойства порождающая процедура, которая описывает способ получения элементов нового множества из уже полученных элементов или из других объектов. Тогда элементами множества считаются все объекты, которые могут быть получены с помощью этой процедуры.
Например, множество  = {1, 2, 4, 8, 16, 32,...} всех чисел, являющихся неотрицательными степенями числа 2 (
= {1, 2, 4, 8, 16, 32,...} всех чисел, являющихся неотрицательными степенями числа 2 ( ), можно задать с помощью порождающей функции по индуктивным правилам:
), можно задать с помощью порождающей функции по индуктивным правилам:
1)  ;
;
2) если 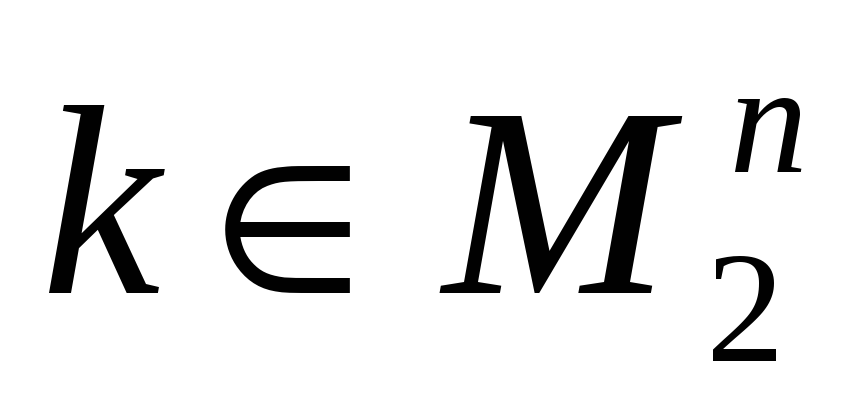 , то
, то  .
.
Итак, запись М={х | P(х)} означает: множество М состоит из всех элементов х, обладающих признаком Р. Например, запись М={x | x3 + Зх2 + 2х = 0} означает, что множество М содержит только корни данного уравнения, т.е. числа {0; -1; -2}. Запись Z= {X | |OX|  4} означает, что для любых X расстояние ОХ меньше или равно 4, т.е. множество всех точек, для которых расстояние до X не больше 4, есть шар с центром в точке О и радиусом R = 4. Запись
4} означает, что для любых X расстояние ОХ меньше или равно 4, т.е. множество всех точек, для которых расстояние до X не больше 4, есть шар с центром в точке О и радиусом R = 4. Запись  читается так: для любых натуральных х, начиная с 7. Отметим, что в записи М={х | P(х)} переменная х является «немой», т.е. несущественной: от нее ничего не зависит. Можно было бы употребить любую другую букву, например у, и все равно это было бы «множество всех элементов, обладающих признаком Р», а как называть элементы — несущественно: главное, чтобы они обладали признаком.
читается так: для любых натуральных х, начиная с 7. Отметим, что в записи М={х | P(х)} переменная х является «немой», т.е. несущественной: от нее ничего не зависит. Можно было бы употребить любую другую букву, например у, и все равно это было бы «множество всех элементов, обладающих признаком Р», а как называть элементы — несущественно: главное, чтобы они обладали признаком.
Если множество не содержит элементов, обладающих характеристическим признаком, то оно называется пустым и обозначается  . Например, множество целых решений неравенства 5 х 6 является пустым:
. Например, множество целых решений неравенства 5 х 6 является пустым:  . Пустым будет множество действительных решений уравнений хг + 25 = 0и52*"3=-1. Множество, не являющееся пустым, называется непустым.
. Пустым будет множество действительных решений уравнений хг + 25 = 0и52*"3=-1. Множество, не являющееся пустым, называется непустым.
Изображение множеств.
Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Элементы множества изображаются точками внутри круга, если они принадлежат множеству (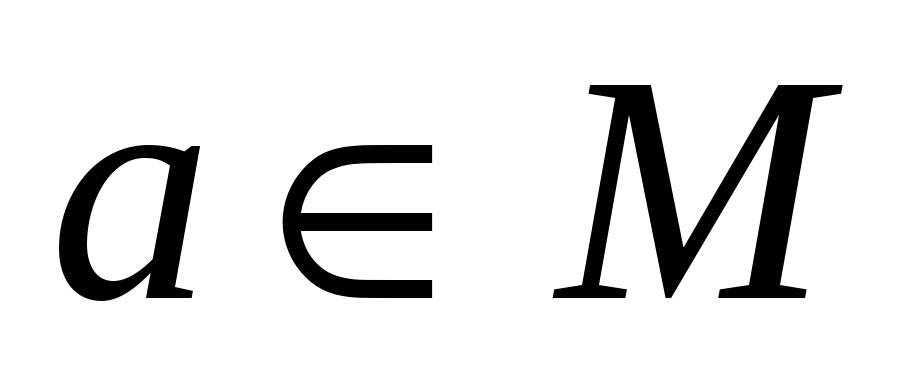 на рис. 1.1, а), и точками вне круга, если они множеству не принадлежат (
на рис. 1.1, а), и точками вне круга, если они множеству не принадлежат (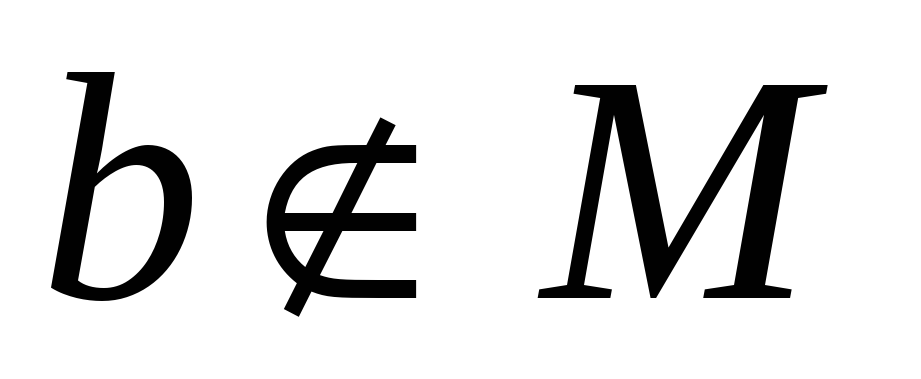 ).
).


а) б)
Рис. 1.1. Иллюстрация кругами Эйлера: а) — элемент а принадлежит множеству М, элемент b не принадлежит множеству М; б) – К подмножество множества М.
Будем также использовать символы  вместо слов «дня любых x», «каждый элемент х» и
вместо слов «дня любых x», «каждый элемент х» и  вместо слов «существует х».
вместо слов «существует х».
Из множества М можно выделить его часть (также выделением нового характеристического свойства или перечислением элементов) - множество К, все элементы которого обладают таким же признаком, как и элементы множества М. Множество К называют подмножеством множества М и обозначают  (рис. 1.1, б). Более строго:
(рис. 1.1, б). Более строго:
Множество К называется подмножеством множества М ( ), если для любого
), если для любого  выполняется
выполняется 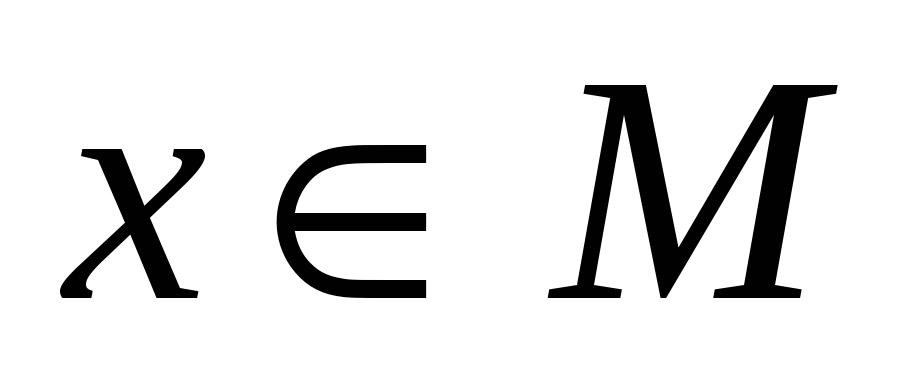 (т.е.
(т.е.  ).
).
Например, добавляя к множеству однозначных целых чисел 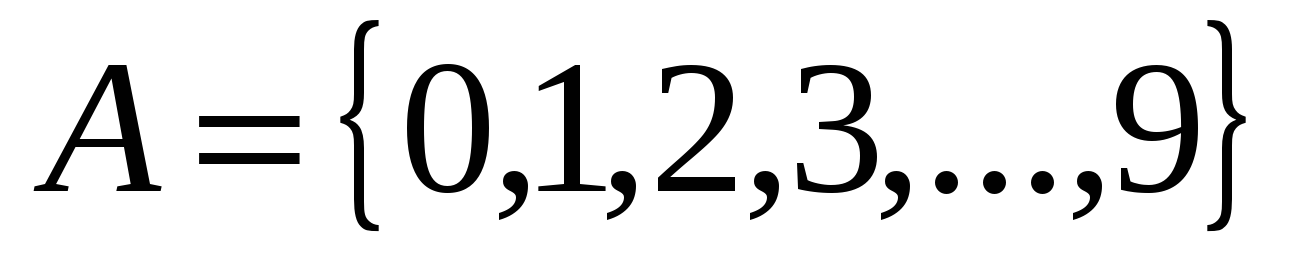 признак «число делится на 3», получаем множество В = {0, 3, 6, 9},
признак «число делится на 3», получаем множество В = {0, 3, 6, 9},  .
.
Так, множество целых чисел Z является подмножеством множества рациональных чисел Q. Для числовых множеств справедливо соотношение:, где N — множество натуральных чисел, Q — рациональных, R — действительных, С — комплексных чисел. Для любого непустого множества М можно сразу указать два его подмножества независимо от состава и структуры М: это оно само и пустое множество. Очевидно, пустое множество содержится (является подмножеством) в любом множестве.
Также необходимо учитывать различие в употреблении знаков включения() и принадлежности () для множества множеств.
Например, М — множество всех специальностей в нашем техникуме, а К— специальность программирования. Хотя К само является множеством (состоит из студентов и сотрудников — преподавателей, администрации и др.), верна запись К М, так как специальность К является элементом всего множества М. Запись К М неверна, так как множества К и М содержат разные элементы: К — людей, М— специальности. Однако, если рассмотрим множество О — совокупность людей со всех специальностей (например, при всеобщем голосовании по насущному вопросу), то, безусловно, К О.
Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком. Например, множество планет Солнечной системы U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун}. Заметим, что понятие универсального множества четко не определено, т. е. некорректно. U можно включить в другое множество W, и оно тоже будет универсальным. Например, долго считалось, что множество действительных чисел R универсально (т. е. описывает всю математику), пока не открыли поле комплексных чисел С и надкомплексные числа и не поняли, что не существует универсального числового множества. Тем не менее там, где область объектов не выходит за рамки некоего множества, иногда бывает удобно оперировать с этим термином. Ведь ржаное поле — вселенная для мыши.
Равными называют два множества А и В, состоящие из одинаковых элементов: А = В.
Например, равны множества решений уравнений 4х-8 = 16, х/15 = 2/5 и 5х-3= 125, так как их решением является одно и то же число 6.
Равны множества букв, из которых составлены слова «навес» и «весна».
Равенство двух множеств А и В означает также, что и  . И наоборот, выполнение свойств и
. И наоборот, выполнение свойств и  означает выполнение равенства А = В. Эти утверждения равносильны.
означает выполнение равенства А = В. Эти утверждения равносильны.
Число элементов множества А называется мощностью множества и обозначается |А| или n(А). Так, мощность пустого множества равна 0: n(0) = 0, а мощность множества планет Солнечной системы n(U) = 9 или |U| = 9.

























