8 класс
Геометрия
Урок № __
Тема: Синус, косинус и тангенс острого угла прямоугольного треугольника.
Тип: урок изучения нового материала.
Основные дидактические цели и задачи: ввести понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника; научить учащихся вычислять значения синуса, косинуса и тангенса для углов 30, 45, 60; развивать способность анализа и вычислительные навыки.
Материал подготовил: Попов Дмитрий Сергеевич.
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга. Проверяется готовность к уроку. Выявление отсутствующих на уроке.
II. Проверка домашнего задания
Учитель берёт тетради для проверки выполнения домашнего задания у 2–3 учащихся.
III. Актуализация опорных знаний учащихся
Фронтальный опрос
– Как называют стороны прямоугольного треугольника? (Сторона прямоугольного треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны – катетами.)
– Назовите свойства прямоугольных треугольников?
– Каким соотношением связаны катеты и гипотенуза прямоугольного треугольника?
IV. Постановка темы и целей урока
– Сегодня мы узнаем значения синуса, косинуса и тангенса в прямоугольном треугольнике.
Учитель записывает на доске тему урока.
V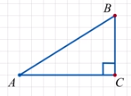 . Изучение нового материала
. Изучение нового материала
– Рассмотрим прямоугольный треугольник АВС. Измерим его
Рассмотрим прямоугольный треугольник АВС. Измерим его
катеты и гипотенузу (АС = 12; АВ = 15; ВС = 9). Разделим длину
катета АС на длину гипотенузы АВ, получим:
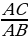 =
= 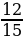 = 0,8.
= 0,8.
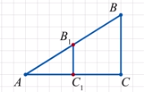
– А теперь возьмём точку С1 на отрезке АС. Проведём к нему
перпендикуляр С1В1. Измерим отрезки АС1 и АВ1:
АС1 = 6 АВ1 = 7,5
Р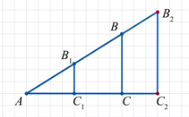 азделим длину катета АС1 на АВ1.
азделим длину катета АС1 на АВ1.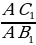 =
= 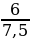 = 0,8.
= 0,8.
Возьмём точку С2 на продолжении отрезка АС и проведём
перпендикуляр С2В2. Измерим отрезки АС2 и АВ2.
Получим: АС2 = 15 АВ2 = 18,75.
Разделим длину катета АС2 на длину гипотенузы АВ2:
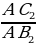 =
= 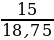 = 0,8.
= 0,8.
Заметим, что катет АС является прилежащим к углу А треугольника АВС.
Катет АС1 является прилежащим к углу А треугольника АС1В1.
Катет АС2 также является прилежащим к углу А, но уже в треугольнике АС2В2.
Получилось, что отношение прилежащего катета к гипотенузе во всех трёх случаях равно 0,8. Очевидно, что это отношение зависит только от угла А.
У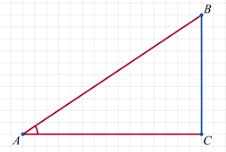 чащиеся записывают определения (подчёркнуты) под диктовку учителя и чертят рисунки:
чащиеся записывают определения (подчёркнуты) под диктовку учителя и чертят рисунки:
Отношение прилежащего катета к гипотенузе cos A = 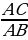
называется косинусом острого угла прямоугольного
треугольника.
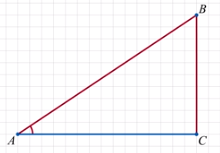
А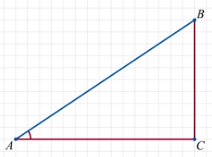 налогично можно найти отношение противолежащего
налогично можно найти отношение противолежащего
катета к гипотенузе. Такое отношение называется синусом sin A = 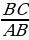
острого угла прямоугольного треугольника.
Отношение противолежащего катета к прилежащему
называется тангенсом острого угла прямоугольного tg A = 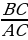
треугольника.
Итак, синус, косинус и тангенс острого угла прямоугольного треугольника это числа. Подумайте, какими числами могут быть синус, косинус и тангенс?
Л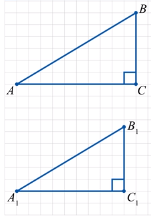 егко доказать, что тангенс угла равен отношению синуса и косинуса этого угла. Проверьте это утверждение, используя определение синуса, косинуса и тангенса.
егко доказать, что тангенс угла равен отношению синуса и косинуса этого угла. Проверьте это утверждение, используя определение синуса, косинуса и тангенса.
Учащийся с быстрыми навыками решения доказывает
Докажем утверждение:
Если острый угол одного прямоугольного треугольника
равен острому углу другого прямоугольного треугольника,
то синусы этих углов равны, а также косинусы этих
углов равны и тангенсы этих углов равны.
Доказательство:
Пусть А = А1 и С и С1 – прямые. Тогда АВС  А1В1С1 (по двум углам), поэтому
А1В1С1 (по двум углам), поэтому 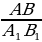 =
= 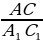 =
= 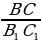 , следовательно
, следовательно 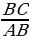 =
= 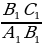 , а это значит sin A = sin A1.
, а это значит sin A = sin A1.
Аналогично из равенства отношений 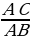 =
= 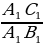 следует равенство соs A = соs A1.
следует равенство соs A = соs A1.
Из равенства отношений 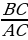 =
= 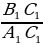 следует равенство tg A = tg A1.
следует равенство tg A = tg A1.
Ч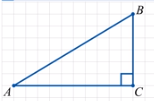 то и требовалось доказать.
то и требовалось доказать.
____________________________________________________________________________
В прямоугольном треугольнике выполняется теорема
Пифагора. Запишем её для треугольника АВС с
прямым углом С:
ВС2 + АС2 = АВ2.
Разделим почленно обе части равенства на АВ2:
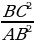 +
+ 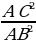 =
= 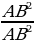 . Получим новое равенство.
. Получим новое равенство.
Используя определение синуса и косинуса угла А получим формулу, связывающую синус и косинус острого угла прямоугольного треугольника. Эта формула называется основное тригонометрическое тождество: sin2 A + соs2 A = 1.
Из основного тригонометрического тождества, зная косинус угла, легко найти его синус, и наоборот.
Например!
Дано: соs A = 0,8.
Найти sin A.
Решение: sin2 A + соs2 A = 1
sin2 A + 0,82 = 1
sin2 A = 1 – 0,82
sin2 A = 0,36
sin A = 0,6.
Ответ: sin A = 0,6.
VI. Закрепление изученного материала. Решение упражнений
1. Работа на карточках (решение упражнений из доп. литературы)
Карточки учитель должен подготовить заранее.
Учащийся со средней успеваемостью решает задание 1 на карточке и диктует решение остальным учащимся.
Учащиеся самостоятельно решают задание 2, по окончании один ученик вслух читает задачу и её решение. Учащиеся его слушают и исправляют ошибки.
| Урок
«Синус, косинус и тангенс острого угла прямоугольного треугольника» Задание №1 
Задание №2

|
2. Решение задач из учебника
№ 591 (а,б) и № 592 (а,в,е) учащиеся решают возле доски.
№593 (а, б) учащиеся решают самостоятельно, а затем коллективно проверяют.
VII. Рефлексия учебной деятельности
– Что называется синусом (косинусом, тангенсом) острого угла прямоугольного треугольника?
– Какое равенство называют основным тригонометрическим тождеством?
– Что вам осталось непонятным из сегодняшнего урока?
VIII. Анонс домашнего задания
Прочитать п. 68
Решить № 591 (в, г), № 592 (б, г, е)
Решить задачу: Гипотенуза АС прямоугольного треугольника АСЕ равна 50,
sin A = 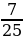 . Найдите площадь треугольника.
. Найдите площадь треугольника.
IX. Подведение итогов урока
Учитель выставляет оценки учащимся за работу на уроке, тем самым подводит итоги урока.







 . Изучение нового материала
. Изучение нового материала Рассмотрим прямоугольный треугольник АВС. Измерим его
Рассмотрим прямоугольный треугольник АВС. Измерим его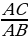 =
= 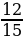 = 0,8.
= 0,8. азделим длину катета АС1 на АВ1.
азделим длину катета АС1 на АВ1.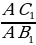 =
= 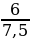 = 0,8.
= 0,8.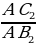 =
= 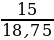 = 0,8.
= 0,8. чащиеся записывают определения (подчёркнуты) под диктовку учителя и чертят рисунки:
чащиеся записывают определения (подчёркнуты) под диктовку учителя и чертят рисунки: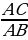

 налогично можно найти отношение противолежащего
налогично можно найти отношение противолежащего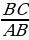
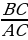
 егко доказать, что тангенс угла равен отношению синуса и косинуса этого угла. Проверьте это утверждение, используя определение синуса, косинуса и тангенса.
егко доказать, что тангенс угла равен отношению синуса и косинуса этого угла. Проверьте это утверждение, используя определение синуса, косинуса и тангенса. А1В1С1 (по двум углам), поэтому
А1В1С1 (по двум углам), поэтому 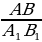 =
= 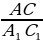 =
= 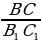 , следовательно
, следовательно 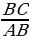 =
= 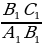 , а это значит sin A = sin A1.
, а это значит sin A = sin A1. 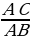 =
= 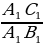 следует равенство соs A = соs A1.
следует равенство соs A = соs A1.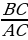 =
= 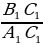 следует равенство tg A = tg A1.
следует равенство tg A = tg A1. то и требовалось доказать.
то и требовалось доказать.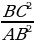 +
+ 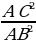 =
= 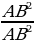 . Получим новое равенство.
. Получим новое равенство.

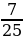 . Найдите площадь треугольника.
. Найдите площадь треугольника.









