| 1 урок. Этапы урока: 1. Организационный этап. Задача. Подготовить учащихся к работе на уроке. Взаимное приветствие учителя и учащихся; проверка подготовленности кабинета и учащихся к уроку; организация внимания учащихся. Учитель. Французский писатель XIX столетия Анатоль Франс однажды заметил: «…Чтобы переваривать знания, надо поглощать их с аппетитом» (Слайд 2). Так давайте на уроке будем активны, внимательны и поглощать знания с большим желанием. 2. Этап подготовки учащихся к активному и сознательному усвоению нового материала (Мотивационный). Учитель. Начнем наш урок с повторения. Игра «Угадай-ка». Я буду вам называть признаки и свойства фигуры или понятия, а вы попробуйте отгадать, что я загадала.
Игра «Угадай-ка». 1.Эта фигура состоит из трех точек и трех отрезков, попарно соединяющих эти точки (треугольник); 2.Это угол, стороны которого образуют прямую и градусная мера его равна 1800.( развернутый угол) 3.Это прямые, которые никогда не пересекаются (параллельные); 4.Это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны (медиана); 5. В этом треугольнике два угла равны (в равнобедренном); 6. В этом треугольнике все углы равны (равносторонний). 7. Накрест лежащие углы ….;(равны) 8. Сумма внутренних односторонних углов равна ….; (180) 3. Этап получения новых знаний. Создание проблемной ситуации - затруднения. (3 мин). Учитель: -Постройте треугольник с углами: 900, 1200, 600. Получится ли треугольник? Нет? Почему? Какой же возникает вопрос? Ученик: -Почему не строится треугольник? Какие должны быть углы у треугольника? Чему равна сумма углов треугольника? Определение темы урока. Постановка цели учащимися (3 мин). Учитель: -Итак, чтобы можно было построить треугольник, сумма углов треугольника должна быть особенной, отличной от тех сумм, которые вы имели сейчас при построении треугольника. А теперь подумайте, чем мы сегодня будем заниматься на уроке, какая тема нашего урока? Ученик: -Тема: Сумма углов треугольника. Какую же цель вы перед собой на уроке можете поставить. Чтобы сформулировать цель, вам помогут незаконченные фразы. «Сегодня на уроке я узнаю…», «Сегодня на уроке я научусь…». Причем мы с вами научимся ставить проблему и выдвигать гипотезу. А что такое гипотеза, как вы думаете? Ученик: Гипотеза – это догадка Проблема: Чему равна сумма углов треугольника? Исследовательская работа учащихся (15 мин). Учитель. -Сегодня каждый из вас побудет в роли исследователя. У нас будет работать 5 лабораторий. Всем лабораториям будут даны разные задания, но все они должны будут сделать один и тот же вывод: выдвинуть гипотезу о сумме углов треугольника. Итак, желаю успеха в вашей научной работе.
Задание для 1 лаборатории: Начертить в тетради остроугольный треугольник, измерить все его углы и найти сумму этих углов. Задание для 2 лаборатории: Начертить в тетради тупоугольный треугольник, измерить все его углы и найти сумму этих углов. Задание для 3 лаборатории: Начертить в тетради прямоугольный треугольник, измерить все его углы и найти сумму этих углов. Задание для 4 лаборатории. Начертить равносторонний треугольник и измерить его стороны. Найти сумму его углов. Задание для 5 лаборатории. Начертить в тетради равнобедренный треугольник, измерить все его углы и найти сумму этих углов.
(Активная работа в группах) А теперь настало время поделиться своими открытиями. (выступают лидеры групп). 4. Доказательство теоремы о сумме углов треугольника (5 мин). Учитель: Итак, группы выдвинули гипотезу: Сумма углов треугольника равна 180. Но, гипотезу надо проверять. Как в геометрии называется гипотеза? (теорема). Итак, сформулируйте теорему: Ученики: «Сумма углов треугольника равна 180». Учитель: Выделите условие и заключение теоремы. Ученики: Сумма углов треугольника – условие, равна 180 – заключение. Учитель: Работа в группах: у вас на парте лежит опорная схема доказательства теоремы. Нужно вставить пропущенные слова. После того, как вы заполните, сделаем взаимопроверку. Вопрос. Кто-нибудь видит на нашем чертеже параллельные прямые? Ответ. Нет. Вопрос. А можно их построить? Ответ. Да. Вопрос. Перечислите возможные варианты построения. Ответ. Через точку А, параллельно ВС. Через точку В, параллельно АС. Через точку С, параллельно АВ. Учитель. Давайте построим прямую MN, проходящую через вершину В, параллельно стороне АС (анимация Слайда 16). В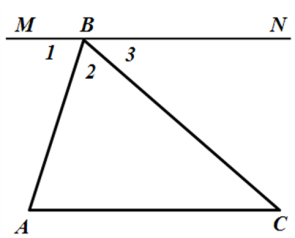 опрос. Какие новые объекты появились? опрос. Какие новые объекты появились? Ответ. 1) прямая MN; 2) углы при прямой MN: 1, 2, 3 (анимация Слайда 16); 3) развернутый угол MBN. Вопрос. Можно ли выделить пары взаимосвязанных углов прямой MN и треугольника АВС? Ответ. 1) 1 и А - внутренние накрест лежащие углы параллельных прямых MN, АС и секущей АВ (анимация Слайда 16), значит, 1 = А, 2) 3 и С - внутренние накрест лежащие углы параллельных прямых MN( анимация Слайда 16), АС и секущей ВС, значит, 3 = С. Учитель. Но из этих фактов пока не следует доказательства теоремы. Рассмотрите угол МВN. Он разбит на три угла: 1, 2, 3. Как в этом случае найти градусную меру 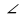 МВN? МВN? Ответ. 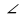 МВN = 1 + 2 + 3 = 180°(анимация Слайда 16). МВN = 1 + 2 + 3 = 180°(анимация Слайда 16). Учитель. Мы уже получили что-то похожее на то, что нужно доказать. А можем ли мы заменить каким-то образом углы 1, 2, 3 на углы треугольника? Ответ. 1 можно заменить на А, 2 – на В, 3 – на С. Вопрос. Какое равенство мы получим в этом случае? Ответ. А + В + С = 180°. Учитель. Что и требовалось доказать. Запись доказательства теоремы. Учащимся предлагается провести дополнительное построение чертежа и сделать в тетрадях краткую запись доказательства теоремы. построим MN || АС, где В 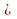 MN; MN; 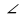 1 = ÐА (внутренние накрест лежащие углы); 1 = ÐА (внутренние накрест лежащие углы); 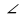 3 = ÐС (внутренние накрест лежащие углы); 3 = ÐС (внутренние накрест лежащие углы); MBN = 1 + 2 + 3 = 180° (развернутый угол); Из 2 – 4 следует: А + В + С = 180°.
Закрепление. Решение задач (5 мин устно). Учитель: -Итак, мы выяснили, что сумма углов треугольника равна 180.
(Задачи – заготовки на листах) Решим устно задачи (группы отвечают поочереди).
 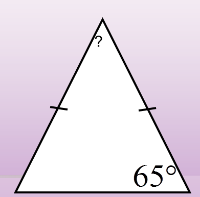  (ученики самостоятельно решают, затем обсуждение ответов с учителем) Учитель: Сколько получилось в первом задание Ученик: 40о Учитель: Во второй? Ученик: Т.к треугольник равнобедренный, то второй угол при основание также будет 65о, значит верхний угол будет равен 180о-(65о+65о)=50о Учитетель: и в третьем случае? Ученик: 800
Подведение итогов Сегодня на уроке мы доказали исследовательским путем теорему о сумме углов треугольника, научились применять приобретенные знания в практической деятельности. Мы еще раз убедились, что геометрия это наука, которая возникла из потребностей человека. Ведь, как писал Галилей: “Природа разговаривает языком математики: буквы этого языка - окружности, треугольники и прочие математические фигуры». Выставление оценок ( 1 мин) . Домашнее задание ( 1 мин). П.31- выучить теорему. Выполнить работу по карточке.  Рефлексия ( 1 мин) Учитель: -чему равна сумма углов треугольника? (180);
Продолжить фразу: Сегодня на уроке я узнал… Сегодня на уроке я научился…
| 






 опрос. Какие новые объекты появились?
опрос. Какие новые объекты появились?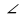 МВN?
МВN? MN;
MN;



















