Конспект урока по геометрии в 7 классе по теме: «Остроугольный, прямоугольный и тупоугольный треугольник. Решение задач»

Урок № 42

ТЕМА: «Остроугольный, прямоугольный и тупоугольный треугольник. Решение задач»

Тип урока: урок комплексного применения знаний и умений.

Продолжительность урока: 45 минут.

Методы обучения: словесный, наглядный, практический, проблемный.

Цели:

• повторить и обобщить знания о треугольнике; доказать теорему о сумме углов треугольника и классифицировать треугольники по углам и сторонам; научиться применять полученные знания при решении задач.

• развивать геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания.

• развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе; содействовать формированию активной жизненной позиции учащихся.

Планируемые результаты:

• Предметные: уметь в процессе реальной ситуации использовать полученные знания при решении задач

• Метапредметные: уметь применять свою наблюдательность, геометрическую интуицию и глазомер; формировать коммуникативную компетенцию учащихся; контролировать и оценивать процесс и результаты своей деятельности.

Универсальные учебные действия:

Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий

• Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев

• Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

• Коммуникативные: умеют активно работать на уроке, слушать собеседника и вести диалог, аргументировать свою точку зрения; умеют работать в сотрудничестве с учителем, друг с другом.

• Личностные: проявляют критичность мышления.

Образовательные технологии, используемые на уроке:

• информационно-коммуникационная;

• проблемно-диалоговая технология; 

• здоровьесберегающая технология (физкультминутка, создание позитивного эмоционального настроя на работу всех учеников в ходе урока; организация различных форм деятельности учащихся, организация урока с учетом временного восприятия и усвоения учебного материала).

Формы работы учащихся: фронтальная, индивидуальная.

Методы обучения:

словесные – беседа, рассказ;

наглядные – демонстрация презентации;

практические – решение задач.

Необходимое оборудование и материалы для урока: компьютер, мультимедийный проектор, раздаточный материал.

ХОД УРОКА:

1. Организационный момент. Мотивация урока.

Учитель. Здравствуйте, ребята, садитесь. Я рада встрече с вами. Вижу у вас хорошее настроение, и я желаю всем на уроке подняться еще на одну ступеньку выше в познании.

- Ни на миг не прерывается живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный нашими предками. Древние греки, на основе наблюдений и из практического опыта, делали выводы, высказывали предположения-гипотезы, а затем на встречах ученых - симпозиумах, эти гипотезы пытались обосновать и доказать. В то время и сложилось утверждение: «В споре рождается истина». Нас сегодняшний урок тоже будет похож на небольшой симпозиум. Мы выскажем своё предположение по вопросу, попытаемся его доказать, и если у нас это получится, то посмотрим, как его можно будет применять при решении задач. А эпиграфом нашего урока, я хочу предложить слова Пифагора:

– Послушайте стихотворение:

Знает даже и дошкольник,
Что такое треугольник,
А уж вам-то как не знать.
Но совсем другое дело –
Быстро, точно и умело
В треугольнике считать:
В нём есть стороны их три
И углов во всех по три
И вершин конечно три.
Если длины всех сторон
Мы сложением найдём
То к периметру придём
Ну, а сумма всех углов
В треугольнике любом
Связана одним числом.

(Учитель держит в руках треугольник) И сегодня мы с вами поговорим о треугольнике, который вдохновлял многих ученых на новые открытия и исследования Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.

2. Мотивация, сообщение темы , цели и задач урока.

Наш урок я хотела бы начать со слов математика современности В. В. Произволова:

«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»

А сегодня мы продолжим говорить о самой главной фигуре в курсе геометрии 7 класса и это… (треугольник). И сегодняшняя тема, также связана с треугольником.

Чтобы узнать о чем мы сегодня будем говорить, вам предстоит решить несколько задач на нахождение углов треугольника. Найдите угол 1 и заполните таблицу в соответствии с ключом на первой странице маршрутного листа.

Вы получили слово КЛАССИФИКАЦИЯ.

Что такое классификация? Распределение по группам, разрядам, классам.

Где вы встречались с этим словом?

Сегодня на уроке мы выясним, как можно классифицировать треугольники.

3. Актуализация знаний

- Внимание на боковую доску. Здесь даны задачи на готовых чертежах. Вам необходимо их решить.

- Но, прежде один из вас сформулирует теорему о сумме углов треугольника. Другой ученик даст определение внешнего угла треугольника и сформулирует его свойство.

- Контроль за уровнем усвоения изученного материала по теме «Сумма углов треугольника».

Задание №1

1) 2) 3) 4)

Задание № 2: Вычислите градусную величину углов 1 и 2 в каждом из треугольников

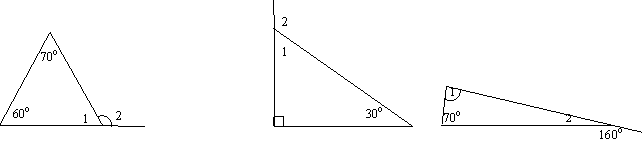Задание № 3: На рисунке даны чертежи к трем задачам и проставлены градусные величины углов. Проверьте, правильно ли указаны числовые данные на каждом из этих рисунков.

- Актуализация опорных знаний

Для актуализации опорных знаний нужно вспомнить виды углов, их градусные меры и теорему о сумме углов треугольника.

На слайде даны углы, а обучающиеся должны определить их вид.

4. Первичное усвоение новых знаний

- Можно ли по видам углов треугольника определить названия треугольников?

(Выслушиваются варианты ответов учащихся)

Рассматривая треугольники с различными углами, выяснить, что прямой и тупой углы в треугольнике могут быть только по одному, а остальные углы - острые.

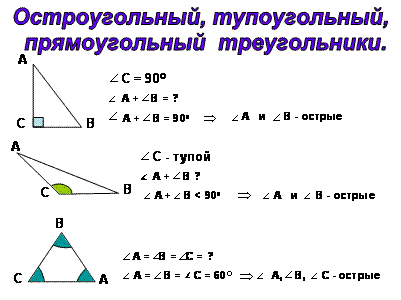
 - Ребята, попробуйте самостоятельно сделать вывод и сформулировать определение острого, прямоугольного и тупоугольного треугольника.

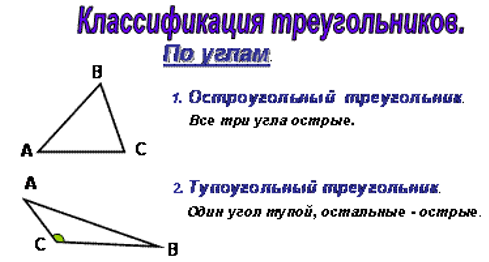
- Итак, дети, мы с вами пришли к такому выводу:

- если все 3 угла треугольника острые, то треугольник называется остроугольным;

- если в треугольнике 1 угол тупой, а 2 других - острые углы, то он называется тупоугольным;

- если в треугольнике 1 угол прямой, то треугольник – прямоугольный.

Вводятся определения остроугольного, тупоугольного, прямоугольного треугольников, понятия гипотенузы и катета прямоугольного треугольника учащимися.

Далее, на слайде показаны верные определения.

Фронтальная работа с классом.
Ученик на доске перемещает слова к треугольникам.
В тетради записать виды треугольников по углам.

- Мы на уроке должны узнать названия сторон прямоугольного треугольника. Итак: две стороны, которые образуют прямой угол, называются катетами; сторона, лежащая против прямого угла, называется гипотенузой.

Вывешиваются на магнитную доску плакаты, на которых нарисованы прямоугольные треугольники. По каждому треугольнику проговариваются названия сторон. Учащиеся перечерчивают к себе в тетрадь.

5. Первичная проверка понимания

Устно решаются задачи на распознавание гипотенузы и катетов.

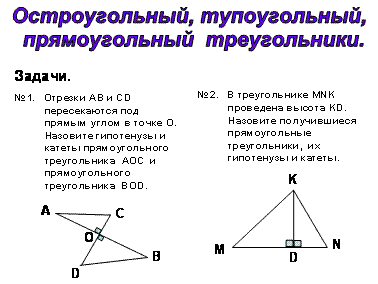
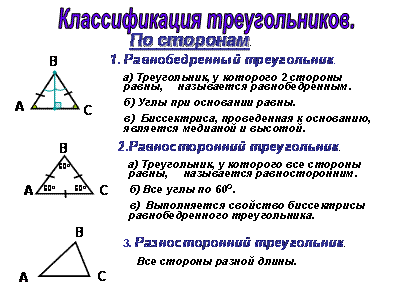
Классификация треугольников по углам и сторонам. Выделяются основные моменты, связанные с каждым видом треугольника.

Учащиеся сами пытаются классифицировать треугольники по углам и сторонам.

Б) организация проектной деятельности (показ презентаций учащимися)

Обозначается проблема: треугольники можно встретить только на страницах учебников и в школьных тетрадях, или эта фигура в разных видах и разных ролях встречается в окружающем мире?

Для решения этой проблемы разработан информационный минипроект, целью которого является с помощью наблюдения, исследования выяснить, где и как, с какой целью применяются человеком треугольники.

    С целью реализации проекта обучающиеся разбились на группы по два человека, определили роли участников (координатор, исследователи, оформитель, ответственный за защиту проекта).

        Предлагается на выбор три темы проекта:

Где и как используются треугольники в строительстве, архитектуре.

Где и как используются треугольники в быту?

Где и как используются треугольники в одежде?

6. Первичное закрепление

а) Выписать все равнобедренные треугольники и их элементы (боковые стороны и основание)
б) Выписать все прямоугольные треугольники и их элементы (гипотенузу и катеты)

Два ученика работают у доски – маркером,
остальные – в раздаточном материале.
Самоконтроль.
Проверка.

Один ученик работает у доски, перемещая треугольники, остальные учащиеся работают в раздаточных материалах – вписывают соответствующие номера треугольников
в таблицу.

В) Конструирование.
Дано восемь треугольников – четыре треугольника с углами 20 и 70 градусов, два треугольника с углами 45 и 45 градусов, два треугольника с углами 30 и 60 градусов. Перемещая данные фигуры, составить треугольники – равносторонний; равнобедренный тупоугольный; равнобедренный прямоугольный; равнобедренный остроугольный.

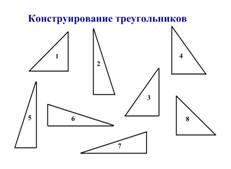
Ученики, перемещая треугольники, конструирует на доске, остальные
с моделями на местах.
Самоконтроль.
Проверка.

Г) Динамическая пауза.
Покажите руками развернутый угол, прямой угол, тупой угол, острый угол, углы 45 и 135 градусов

Д) Пиши грамотно.
В геометрические термины, используемые на уроке вписать пропущенные буквы.
Открыть «шторку» и проверить правильность написания.

Один человек работает маркером у доски.
Остальные в раздаточном материале. Самоконтроль.

7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция

Учитель с учениками обсуждают ошибки, сделанные на уроке учащимися.

8. Информация о домашнем задании, инструктаж по его выполнению: п. 32 №223 (б,в);

№227 (а);№230

9. Рефлексия (подведение итогов занятия)

Продолжить фразу. Подвести итог урока.

Ученики, перемещают слова – узнал, удивился, научился, задумался, повторил, запомнил, и устно завершают фразу.

Какие углы называются смежными?

Какие виды треугольников вы знаете?

Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?

Какой треугольник называется равнобедренным?

Могут ли быть смежными тупой и прямой углы? Почему?

Какие углы могут образоваться при пересечении улиц?

Приложение

Устный тест

1. В треугольнике АВС угол А равен 90°, при этом другие два угла:

а) один острый, а другой может быть

прямым;

б) оба острые;

в) один острый, а другой может быть

тупым .

2. В треугольнике АВС угол В - тупой, при этом другие два угла могут быть:

а) только острыми;

б) острый и прямой;

в) острый и тупой.

3. В остроугольном треугольнике могут быть:

а) все углы острые;

б) один тупой угол;

в) один прямой угол.

Учитель предлагает обучающимся устно решить задачи по готовым чертежам

1. В треугольнике ABC угол A равен 30^o, угол B равен 90^o. Найдите угол C.(60)

2. В треугольнике ABC угол C равен 120^o, AC = BC. Найдите угол A.(30)

3. В треугольнике ABC угол A равен 40^o, AC = BC. Найдите угол C.(100)

4. В треугольнике ABC AC = BC, угол C равен 50^o. Найдите внешний угол CBD. (115)

5. В треугольнике ABC угол A равен 40^o, внешний угол при вершине B равен 100^o. Найдите угол C. (60)

6. В треугольнике ABC AB = BC. Внешний угол при вершине B равен 140^o. Найдите угол C.(70)

7. Углы треугольника относятся как 1:2:3. Найдите меньший из них.(30)

8. Для черепичных крыш угол между двумя стропилами берут равным приближённо 90º. Определите, какой высоты будет крыша, если ширина дома 10 м? (5м)

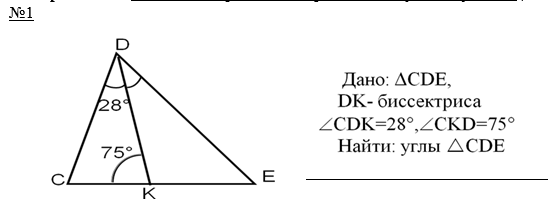
№2 Дано: АВС-

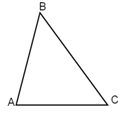треугольник

А: В: С = 2:3:4

Найти: А, В, С.

Решение: Пусть одна часть составляет х⁰. Тогда А=(2х)⁰,В=(3х)⁰,С=(4х)⁰. Зная, что по теореме о сумме углов треугольника А + В+ С=180⁰, составлю и решу уравнение.

2х+3х+4х=180,

9х=180,

х=20,

А=40⁰, В=60⁰, С=80⁰.

Ответ:40⁰,60⁰,80⁰.

Фронтально:

1. Назовите элементы треугольника:

вершины, стороны, углы.

2. Какой угол называется острым, тупым, развернутым, прямым?

• Градусная мера острого угла меньше 90 градусов;

• Градусная мера тупого угла больше 90 градусов, но меньше 180 градусов;

• Градусная мера прямого угла равно 90 градусов.

3. Свойства смежных углов:

Сумма смежных углов равна 180 градусов.

4. Свойства вертикальных углов:

Вертикальные углы равны.

5. Определение внешнего угла треугольника:

Угол, смежный с углом треугольника.

6. Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

7. Какой треугольник называется равнобедренным,

Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине.

8. Как называются равные стороны в равнобедренном треугольнике?

Боковые стороны.

9. Свойство углов у основания равнобедренного треугольника?

Углы при основании равнобедренного треугольника основания равны.

10. Какой треугольник называется равносторонним?

Равносторонний треугольник — это треугольник, в котором все стороны равны между собой по длине.

11. Свойства углов равностороннего треугольника .

Углы равностороннего треугольника равны.

11