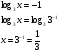Конспект урока по математике в 11 классе по теме «Логарифмические уравнения и основные методы решения»
| Тема урока | Логарифмические уравнения и основные методы решения |
|
| Тип урока | Урок изучения нового материала |
|
| Цель урока | Организовать учебную деятельность по изучению методов решения логарифмических уравнений, используя определение логарифма, метод потенцирования, метод введения новой переменной. |
|
| Задачи Общеобразовательные | Обеспечить в ходе урока формирование умений и навыков решения логарифмических уравнений, закрепление новых понятий: логарифмическое уравнение, методы решения логарифмических уравнений; научить учащихся решать логарифмические уравнения методом, основанным на определению логарифма, методом потенцирования |
|
| Развивающие | Способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти. Развивать грамотную математическую речь при ответе у доски и с места |
|
| Воспитательные | Воспитывать аккуратность, чувство ответственности, умение рационально, аккуратно оформить задание на доске и в тетради. содействовать воспитанию интереса к математике, активности, умению общаться, аргументировано отстаивать свои взгляды, воспитанию взаимовыручки, воспитании у учащихся, уверенности в себе, веры в свои силы |
|
| Оборудование урока | учебник, карточки, ТСО ПК, мультимедийный проектор, учебник раздаточные материалы (для самостоятельной работы) |
|
|
| Этапы урока |
|
|
|
| Организационный момент | Приготовить доску, тетради, учебное пособие, таблицы, ТСО |
|
|
| Этап актуализации знаний. Опрос
| 1.Теоретическая разминка. Дайте определение логарифма числа? Перечислите основные свойства логарифмов? Дайте определение логарифмической функции? Дайте определение допустимых значений логарифмической функции Перечислите основные свойства логарифмической функции? 1.Устный счёт-конкурс «Лучший счётчик» На доске записаны примеры на вычисление логарифмических выражений. выигрывает тот, кто решит больше примеров за 1 минуту.
| Учащиеся отвечают на вопросы |
|
| Устная работа
| Задания на интерактивной доске (презентация) Вычислить а) log28 б) lg 0,01; в) 2 log 2 32. 3 log 34 = log 4 4 = log 3 1 = log -5 5= log 4 1= log 6 6 = log 3 27 = ) 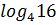 6) 6) 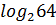 2) 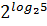 7) 7) 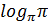 log 2 32 = . �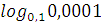 � . � � . �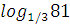 � �
7. �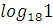 � �
8. �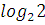 � � 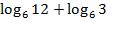
log 15 3 + log 15 5 �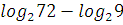 � � log 6 2 + log 6 3 = log 2 28 - log 2 7 = 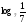 log 2 15 - log 2 30� log 2 15 - log 2 30�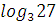 � �
3) 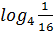 8) 8) 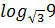 4) 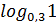 9) ℓg ℓg10 9) ℓg ℓg10 5) 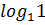 1) 1)  4) 4) 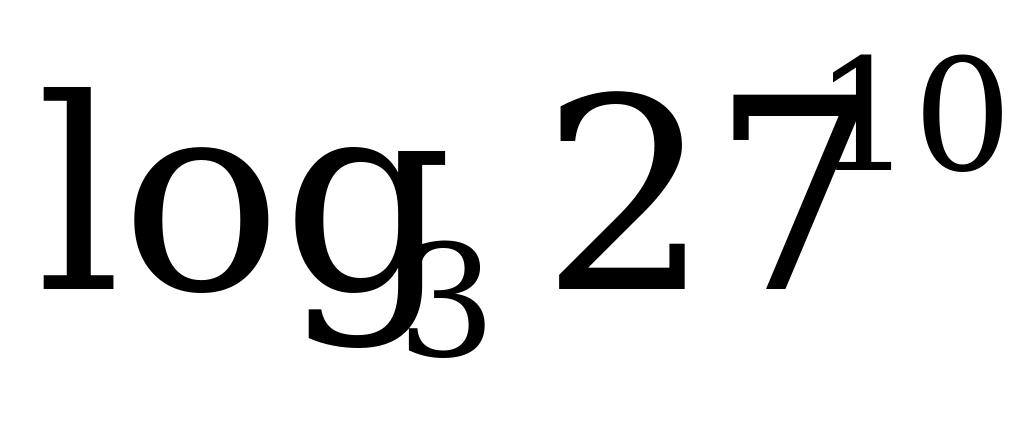 7) 7) 
2) 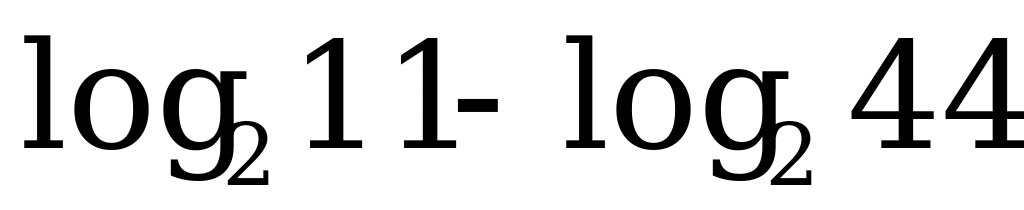 5) 5) 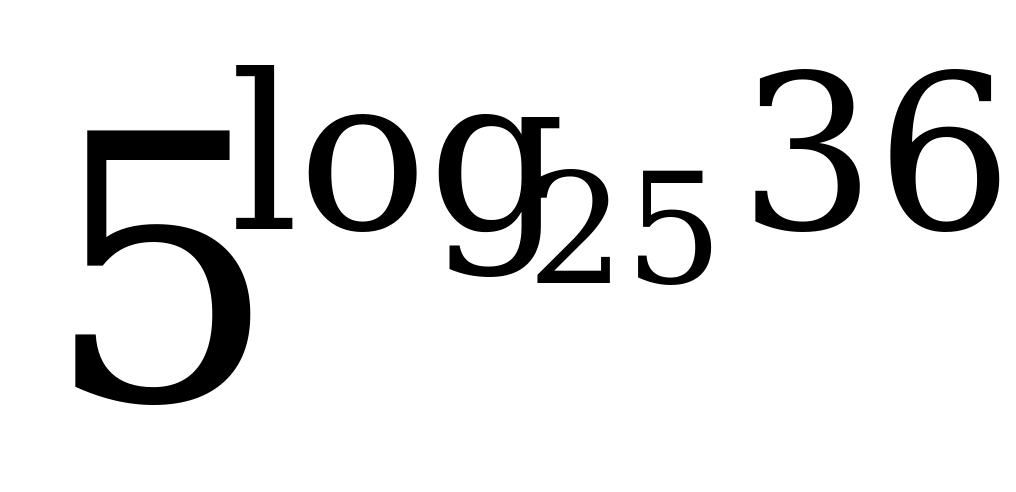 8) 8) 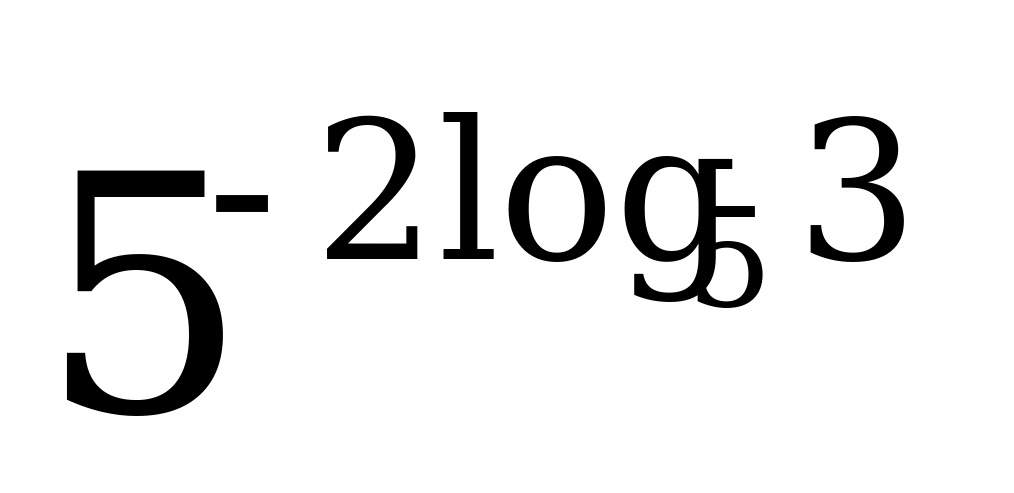
3) 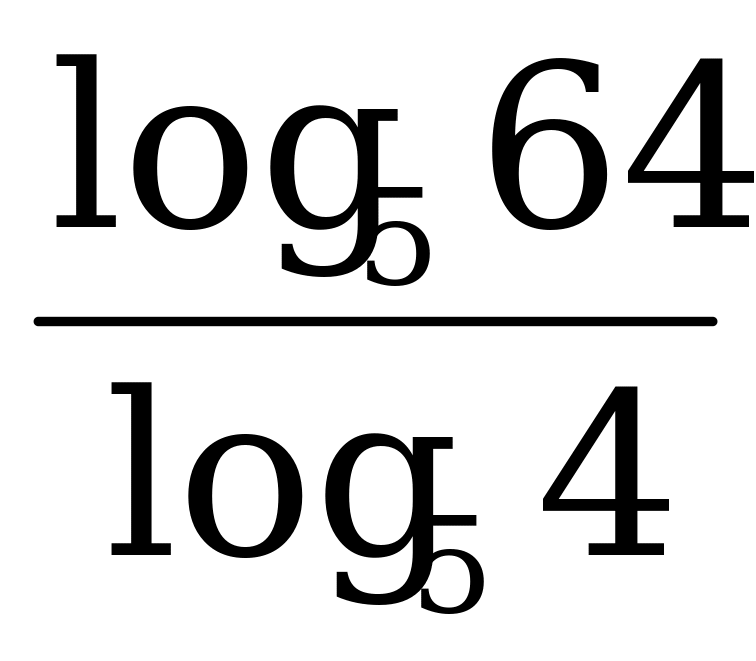 6) 6) 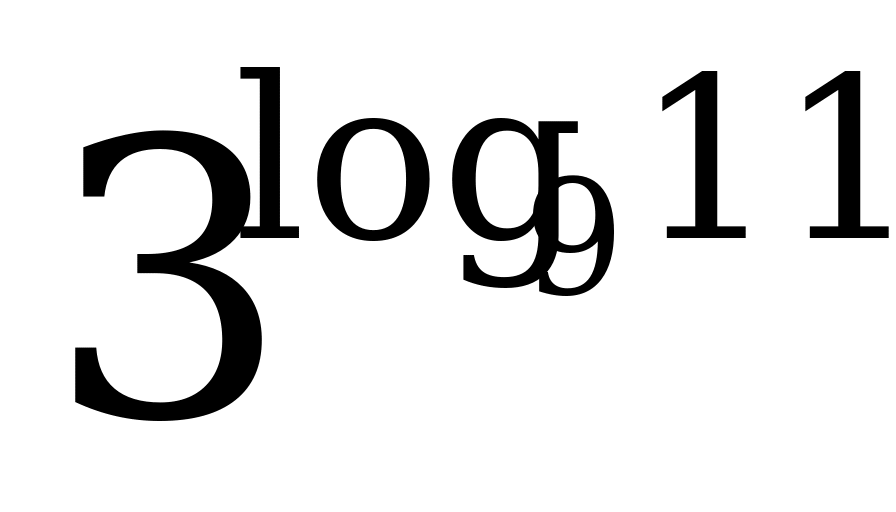 а) log 2 64; б) log 3 а) log 2 64; б) log 3 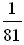 ; в) log 7 718; ; в) log 7 718; г) 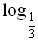 1; д) 1; д) 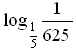 ; е) ; е) 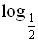 512; 512; ж) lg 0,0007; з) lg (3 · 10–23); и) lg 4 + lg 25.
а) log 4 16; б) 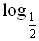 256; 256; в) log 3 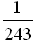 ; г) log 2 6 + log 2 ; г) log 2 6 + log 2 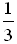 ; ; д) 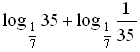 ; е) log 4 168 – log 4 84. ; е) log 4 168 – log 4 84. 2. Решите уравнение.
а) lg2 x – lg x – 2 = 0;
а) log28 б) lg 0,01; в) 2 log 232. 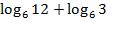 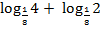 (1б) (1б) 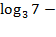 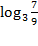 (1б) (1б) 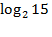 - - 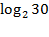 (1б) (1б) 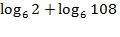 (1б) (1б) 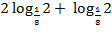 (1б) (1б) 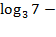 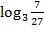 (1б) (1б) 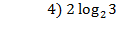 - - 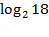
| Учащиеся отвечают устно |
|
| Самостоятельная работа Подготовка к ЕГЭ
| Учитель задает вопросы ученикам: Дайте определение уравнение, корень уравнения, Что значит решить уравнение? Найти все значения переменной, при которых уравнение обращается в верное числовое равенство или доказать, что таких значений нет. Что такое корень уравнения? Значение переменной, при которой уравнение обращается в верное числовое равенство. Самостоятельно решить задания из тестов ЕГЭ №7, Вычислить. Решить уравнения. показательные уравнения способом приравнивания коэффициентов
| Учащиеся отвечают на вопросы |
| Самостоятельная работа Подготовка к ЕГЭ . | Учащимся даны карточки, на которых уравнения из банка заданий ЕГЭ | Учащиеся называют вид каждого уравнения и прорешивают их |
| Физкультминутка
| Для того, чтобы перейти к следующему этапу нашей работы и успешному её выполнению, давайте немножко отдохнём. (Слайд 21) Сильно зажмурьте глаза, откройте глаза и посмотрите на предмет перед вами (повторите 5 раз). Закройте глаза, откройте глаза, посмотрите направо, посмотрите налево (повторите 5 раз). Сильно зажмурьте глаза, откройте глаза и посмотрите на предмет вдали от вас (повторите 5 раз). Формирование умения сотрудничать с одноклассниками, умения координировать свои действия.
|
|
| Взаимопроверка | Ответы даны на интерактивной доске | Учащиеся проверяют работы друг друга и выставляют оценки |
|
| Этап объяснения нового материала Изучение нового материала с помощью опорных конспектов | Создание проблемной ситуации. Учитель: Ребята, у нас возникла проблема. Мы не решили одно из уравнений, в котором есть знак логарифма и под знаком логарифма находится переменная. Как вы думаете, как называются такие уравнения? Записали тему урока: Логарифмические уравнения. Учитель дает определение: Уравнения, в которых переменная содержится под знаком логарифма, называют логарифмическими. Существует несколько способов решения логарифмических уравнений. Мы сегодня рассмотрим три способа решений: 1 Решения логарифмических уравнений на основании определения логарифма 2 Решения логарифмических уравнений методом потенцирования: 3 Решения логарифмических уравнений методом введения новой переменной
Каждому ученику учитель выдает опорный конспект. 1. Решения логарифмических уравнений на основании определения логарифма. Для уравнения вида �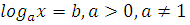 �получаем � �получаем �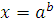 � единственный корень. Пример. � единственный корень. Пример. 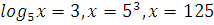 Для уравнения вида �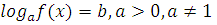 �получаем равносильное уравнение � �получаем равносильное уравнение �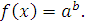 � Пример. � Пример. 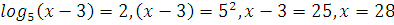 2. Для решения уравнений используется еще метод: потенцирования. Этот метод применяется для уравнений вида 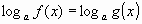 и сводится к решению уравнения f(x)=g(x), Необходима проверка корней или х должен удовлетворять решению системы. Пример решения уравнения вторым методом. log 2 (3x – 6) = log 2 (2x – 1); и сводится к решению уравнения f(x)=g(x), Необходима проверка корней или х должен удовлетворять решению системы. Пример решения уравнения вторым методом. log 2 (3x – 6) = log 2 (2x – 1); 3x – 6 = 2x + 1, где 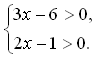 3x – 2x = –1 + 6; х = 5 – удовлетворяет ОДЗ. log3 (7x – 9) = log3 x; 7х – 9 = х 6х = 9 х = 1,5 Проверим найденные корни по условиям 7х-90 и x0 3. На какое уравнение похоже логарифмическое уравнение данного вида? Данное уравнение похоже на квадратное уравнение. 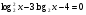 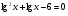 Каким образом нам из этого уравнения получить квадратное? Каким образом нам из этого уравнения получить квадратное? - -Ввести новую переменную. 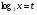 Получим квадратное уравнение: Получим квадратное уравнение: 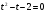 Вычислим дискриминант Вычислим дискриминант 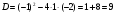 Найдём корни квадратного уравнения Найдём корни квадратного уравнения 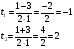 Решим простейшие логарифмические уравнения: Решим простейшие логарифмические уравнения:
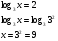 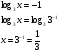 Оба корня положительные, являются решением уравнения. Ответ: : х1 = 1/3, х2 = 9
Осмысление, систематизация полученных знаний Фронтальная работа
| 2.Выявление проблемы. Формулируют ответы на поставленные вопросы
Учащиеся записывают
Осмысление, систематизация полученных знаний Фронтальная работа
|
|
|
| log 2(3x – 6) = log 2(2x – 3) lg 2 х2 + lgx2 – 6 = 0 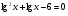 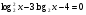 lg2 x – lg x – 2 = 0; 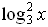 – log 3 x – 6 = 0; – log 3 x – 6 = 0;
|
|
|
| Первичное закрепление Самостоятельная работа (дифференцированная)
| На доске записаны три уравнения, которые нужно решить изученными способами. | В-1 | В-2 | | 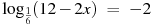 , х = – 12 , х = – 12
| 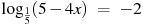 , х = 5 , х = 5
| | 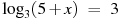 , х= – 22 , х= – 22
| 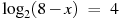 , х = – 8 , х = – 8
| | 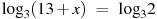 , х = – 11 , х = – 11
| 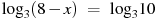 , х = – 2 , х = – 2
| | 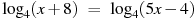 , х = 3 , х = 3
| 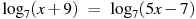 , х = – 4 , х = – 4
|
| Учащиеся по очереди решают. Предъявление решений уравнений на доске, обсуждение, коррекция оформления, записи в тетрадях. |
|
| Закрепление | Решите уравнения 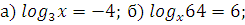 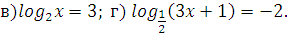 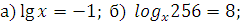 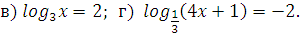 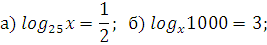 log 6 (14 – 4x) = log 6 (2x + 2); 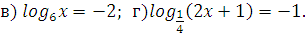 а) log 3 (x2 + 6) = log 3 5x а) log 0,1 (x2 + 4x – 20) = 0; а) log 3 (x2 – 11x + 27) = 2; а) log 2 (x2 + 7x – 5) = log 2 (4x – 1); б) log 0,3 (–x2 + 5x + 7) = log 0,3 (10x – 7); Решите уравнение. 1. log 2 (4x + 5) = log 2 (9 – 2x). 2. log 3 (x2 – 5x – 23) = 0. 3. lg (x + 2) + lg (x – 2) = lg (5x + 10). Вариант 2 Решите уравнение. 1. log 5 (3x – 4) = log 5 (12 – 5x). 2. log 3 (x2 + 3x – 7) = 1. 3. lg (x – 1) + lg (x + 1) = lg (9x + 9). Вариант 3 Решите уравнение. 1. lg (5x – 4) = lg (1 – x). 2. 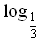 (x2 + 3x – 9) = –2. (x2 + 3x – 9) = –2. 3. 1 + log 2 (x + 1) = log 2 (7x + 2) – log 2 (x – 1). Вариант 4 Решите уравнение. 1. lg (3x – 10) = lg (7 – 2x). 2. log 0,5 (x2 – 4x + 20) = –5. 3. 1 + log 3 (x – 2) = log 3 16x – log 3 (x + 2). а) 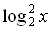 – 4 log 4 x + 3 = 0. – 4 log 4 x + 3 = 0. б) 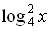 – log 4 x – 2 = 0. – log 4 x – 2 = 0. г) 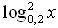 + log 0,2 x – 6 = 0. + log 0,2 x – 6 = 0. а) log x (2х2 + х – 2) = 3. б) log x – 1 (12х – х2 – 19) = 3. а) 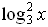 – log 3 x – 6 = 0; а) lg2 x – lg x – 2 = 0; а) 2 – log 3 x – 6 = 0; а) lg2 x – lg x – 2 = 0; а) 2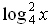 + 5 log 4 x – 3 = 0; а) + 5 log 4 x – 3 = 0; а) 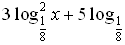 x – 2 = 0; x – 2 = 0;
| Предъявление решений уравнений на доске, обсуждение, коррекция оформления, записи в тетрадях. |
|
| Самостоятельная работа (дифференцированная) | Самостоятельная работа Вам предложены уравнения. Ваша задача решить эти уравнения и соотнести ответы с соответствующей буквой. В результате должно получиться слово. Обращаю ваше внимание, что уравнения взяты из демоверсий ЕГЭ, задание В3. 1.  (-1, – 3) (-1, – 3) 2. 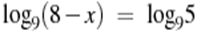 (х=3) (х=3) 3. 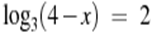 (х=-5) (х=-5) 4.  (х=3) (х=3) 5. 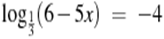 (х=-15) (х=-15) Ключ | 3 | -2 | -3, – 1 | -15 | -7 | -1 | -5 | 0 | 12 | | Е | А | Н | Р | Д | О | П | З | Л | Джон Непер
| Самостоятельная работа (дифференцированная) |
|
| Доклад по теме: «Из истории логарифмов» | НЕПЕР Джон (1550-1617) , шотландский математик, изобретатель логарифмов. Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий. В 1590- х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд "Описание удивительных таблиц логарифмов" опубликовал лишь в 1614 году. В конце 1620-х годов была изобретена логарифмическая линейка, счетный инструмент, использующий таблицы Непера для упрощения вычислений. С помощью логарифмической линейки операции над числами заменяются операциями над логарифмами этих чисел Об истории развития логарифмов Слово логарифм происходит от слияния греческих слов и переводится как отношений чисел, одно из которых является членом арифметической прогресс, а другое геометрической. Впервые это понятие ввел английский математик Джон Непер . Кроме того, этот человек известен тем, что он первый изобрел таблицу логарифмов, которая пользовалась большой популярностью среди ученых на протяжении долгих лет. В таблицы Непера, изданные в книгах под названием «Описание удивительной таблицы логарифмов» и «Устройство удивительной таблицы логарифмов», вошли значения логарифмов синусов, косинусов и тангенсов углов от 0 до 99 градусов. Первые таблицы десятичных логарифмов были составлены в 1617 г. английским математиком Бриггсом. Многие из них были выведены с помощью выведенной Бриггсом формулы. Изобретатели логарифмов не ограничились созданием логарифмических таблиц, уже через 9 лет после их разработки в 1623 г. Английским математиком Гантером была создана первая логарифмическая линейка. Она стала рабочим инструментом для многих поколений. В настоящее время мы можем находить значения логарифмов, используя компьютер |
|
|
| Проверочная работа.
Итоги урока. рефлексия | Вопросы учащимся: Какие уравнения называются показательными? Простейшими показательными? Назовите основные методы решения уравнений.
|
|
|
| Задание на дом | Домашнее задание. Возьмите карточки с разноуровневым дом задание. Кто желает может взять все уровни. 1 уровень · log 3 x= 4 · log 2 x= -6 · logx 64 = 6 · – log x 64 = 3 · 2 log x 8 + 3 = 0 2 уровень · log 3 (2х – 1) = log 3 27 · log 3 (4х+5)+log 3 (х +2) = log 3 (2х +3) · log 2 х = – log 2 (6х – 1) · 4 + log 3 (3-х) = log 3 (135–27х) · log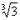 (х – 2) + log 3 (х – 2) = 10 (х – 2) + log 3 (х – 2) = 10 3 уровень · 2log 2 3 х – 7 log 3 х + 3 = 0 lg 2 х – 3 lg х – 4 = 0 · log 2 3 х – log 3 х – 3 = 2 lоg 2 3 |
|
|
|
| “Сегодня на уроке я научился…”
“Сегодня на уроке я познакомился…”
“Сегодня на уроке я повторил…”
“Сегодня на уроке я закрепил…” На партах у вас есть кружки голубого, оранжевого и розового цвета. Оцените себя за деятельность на уроке. 3-гол цвет, 4- желтый, 5 – розовый.
|





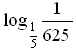 ; е)
; е) 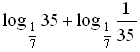 ; е) log 4 168 – log 4 84.
; е) log 4 168 – log 4 84.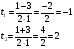 Решим простейшие логарифмические уравнения:
Решим простейшие логарифмические уравнения: