Конспект урока по теме "Дисперсия и стандартное отклонение".

Урок вероятность и статистика в 11 классе. Учитель Гончарова Е.Б.

Тема: «Дисперсия и стандартное отклонение».

Цели:

Познавательные

– закрепить полученные знания и умения, применять статистические характеристики при решении простейших задач;

• показать значимость этой темы в практической деятельности человека;

развивающие – развитие математически грамотной речи, логического мышления;

воспитательные – подготовка учащихся к проблемам современной жизни, воспитание познавательной активности, культуры диалога.

Задачи:

вооружить учащихся системой знаний по теме "Определение вероятности событий, среднего арифметического и медианы набора чисел";

сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;

сформировать навыки самостоятельной работы.

ХОД УРОКА

1. Мотивационная беседа с учащимися.

“Статистика знает всё”, – утверждали Ильф и Петров в своем знаменитом романе “Двенадцать стульев” и продолжали: “Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических таблиц!..” Это ироническое описание дает довольно точное представление о статистике (от лат. status – состояние) – науке, изучающей, обрабатывающей и анализирующей количественные данные о самых разнообразных массовых явлениях в жизни. Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления. Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий. Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный). А еще есть статистика финансовая, налоговая, биологическая, метеорологическая.

Мы с вами рассматриваем понятия и методы описательной статистики, которая занимается первичной обработкой информации и вычислением наиболее показательных числовых характеристик. По словам английского статистика Р. Фишера: “Статистика может быть охарактеризована как наука о сокращении и анализе материала, полученного в наблюдениях”. Всю совокупность числовых данных, полученных в выборке можно (условно) заменить несколькими числовыми параметрами, некоторые из них мы уже рассматривали на уроках – это среднее арифметическое, размах, мода и медиана. Результаты статистических исследований широко используются для практических и научных выводов, поэтому важно уметь определять эти статистические характеристики.

2. Актуализация опорных знаний.

Игра «Математическая перестрелка»

Каждой команде предлагается ответить на вопросы и выполнить следующие задания.
На доске два ряда чисел , по одному для каждой команды.

“+”: 8, 3, 8, 5, 1.
“0”: 7, 5, 6, 10, 2.

1. Что называется средним арифметическим ряда чисел? (Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.)

2. Может ли среднее арифметическое ряда чисел не совпадать ни с одним из этих чисел? (Среднее арифметическое может не совпадать ни с одним из этих чисел.)

3. Что называется размахом ряда чисел? (Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.)

4. Что называется модой ряда чисел? (Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.)

5. Любой ли ряд чисел имеет моду? (Ряд чисел может не иметь моды.)

6. Может ли ряд чисел иметь более одной моды? (Числовой ряд может иметь более одной моды, такой ряд – полимодальный.)

7. Может ли мода ряда чисел не совпадать ни с одним из этих чисел?(Мода, если она существует, обязательно совпадает с двумя или более числами ряда.)

8. Что называется медианой ряда чисел? (Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине; медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.)

9. Может ли медиана числового ряда не совпадать ни с одним из этих чисел? (Медиана ряда чисел может не совпадать ни с одним из этих чисел.)

10.  Определить статистические характеристики для записанных на доске числовых рядов.

(“+”: ранжированный ряд 1, 3, 5, 8, 8. х = (1 + 3 + 5 + 8 + 8): 5 = 5; Мо = 8; Ме = 5; размах = 8 – 1 = 7.
“0”: ранжированный ряд 2, 5, 6, 7, 10. х = (2 + 5 + 6 + 7 + 10) : 5 = 6; Мо – нет; Ме = 6; размах = 10 – 2 = 8).

3. Изучение нового материала.

Дисперсия и среднее квадратичное отклонение

При анализе результатов исследований полезно иметь представление о разбросе данных в числовом ряду. Размах ряда один из таких показателей, но дает слишком грубую оценку.

Размах ряда чисел – разность между наибольшим и наименьшим числами в данном ряду чисел.

Рассмотрим наиболее часто используемый на практике статистический показатель – дисперсия.

Представлен ряд чисел 4; 8; 12; 7; 16; 13.

Вычислим среднее арифметическое данного ряда. Сумму всех чисел ряда разделим на их количество.

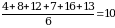
Вычислим отклонение каждого члена ряда от среднего арифметического:

4 – 10 = –6;

8 – 10 = –2;

12 – 10 = 2;

7 – 10 = –3;

16 – 10 = 6;

13 – 10 = 3.

Заметим, что сумма отклонений равна нулю:

(–6) + (–2) + 2 + (–3) + 6 + 3 = 0.

Данный показатель не может характеризировать разброс данных, так как для любого ряда чисел он всегда будет равен нулю.

Составим ряд квадратов отклонений и рассчитаем среднее арифметическое ряда, т. е. определим дисперсию заданного ряда данных.

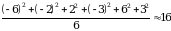
Дисперсия рассматриваемого ряда равна 16.

Дисперсией ряда чисел называется среднее арифметическое квадратов их отклонений от среднего арифметического этого ряда.

Дисперсия – мера разброса чисел в ряду.

Рассмотрим пример.

Кто лучше готов к соревнованиям?

Спортсмены проводили подготовку к соревнованиям по стрельбе из лука. Оба спортсмена произвели по 7 серий выстрелов. Каждая серия состояла из 12 выстрелов. По итогам каждой серии подведены результаты попадания в цель.

Получили следующие данные:

Спортсмен 1: 11, 11, 12, 11, 9, 11, 12.

Спортсмен 2: 12, 10, 9, 12, 11, 12, 11.

Найдём среднее арифметическое для каждого спортсмена.

Спортсмен 1: .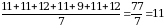

Спортсмен 2: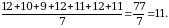

Значения одинаковы.

Вычислим дисперсию результатов для каждого спортсмена.

Спортсмен 1:

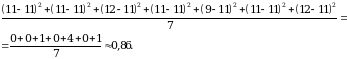
Спортсмен 2:

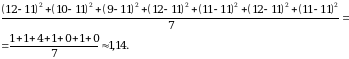
Обратите внимание на полученные значения.

Разброс данных у первого спортсмена меньше. Это говорит о его лучшей подготовке.

Данный пример демонстрирует, что при равных средних арифметических значениях, именно дисперсия позволила выявить наименьший разброс данных среди результатов.

Первый спортсмен лучше готов. Показал более стабильный результат.

Отметим особенность дисперсии.

Если в ряду содержится большое число данных, среди которых есть лишь несколько данных, значительно отличающихся от среднего арифметического этого ряда, то дисперсия такого ряда данных обычно не велика.

Недостаток дисперсии.

Если исследуемые величины измеряются в каких-либо линейных единицах измерения: килограммах, метрах, часах и т. д., то по сущности вычислений дисперсия измеряется в квадратах этих единиц, т. е. некоторые из этих единиц измерений не имеют реального смысла.

Поэтому дисперсию часто заменяют на среднее квадратичное отклонение.

Средним квадратичным отклонением числового ряда называют квадратный корень из дисперсии этого ряда.

Запишем результаты для рассматриваемого нами примера.

Спортсмен 1: .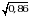

Спортсмен 2: .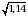

Среднее квадратичное отклонение принято обозначать греческой буквой  (сигма).

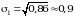
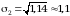
4. Итог урока, рефлексия.

5. Домашнее задание.

Дополнительно.

Метод сравнения средних значений и дисперсий используется в самых разных отраслях человеческой деятельности. В медицине – для установления диагноза, в литературоведении – для определения автора произведения (когда авторство является спорным), в криминалистике – для розыска преступников.

Пример. Органами милиции задержан грузовик с помидорами, похищенными на овощной базе. В городе всего четыре базы, каждая из них получает помидоры из своего сельскохозяйственного района. Определите, с какой базы были вывезены помидоры. Расследование осложняется тем, что помидоры на всех базах одного сорта.

Решение.

Воспользуемся методом сравнения средних значений и дисперсий. В каждом сельскохозяйственном районе свои условия произрастания помидоров, поэтому помидоры разных районов отличаются, скажем, удельным весом (диаметром, весом и др.). Выберем по 20 – 25 помидоров (реально, конечно, больше) на каждой овощной базе и из грузовика. У нас получатся 4 последовательности – по одной для каждой базы, и еще одна – для грузовика, с которого мы и будем сравнивать первые четыре. Это наши исходные данные. Результатом является номер овощной базы, где совершено хищение.

Чтобы добиться этого результата, нужно, как рассказано выше, вычислить средние значения и дисперсии всех пяти последовательностей и провести сравнение.

Пусть вес 1 помидора на соответствующих базах и в грузовике изменяется в пределах (в г):

1-я (70, 100)
2-я (80, 90)
3-я (75, 95)
4-я (90, 120
Грузовик (80, 90).

Сравнивая, замечаем, что дисперсии и средние одновременно близки у грузовика и второй базы. Значит, помидоры украдены со второй базы.
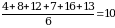
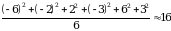
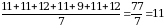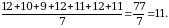
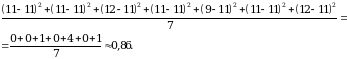
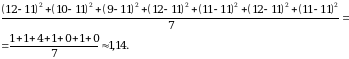
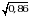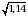