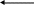Республика Коми, г.Сыктывкар
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 14.05.2025 13:19
Сметанина Татьяна Валерьевна
Преподаватель Физики
38 лет
170
170 720 
Местоположение
Специализация
Конспект урока по теме: "Равномерное движение по окружности"
Категория:
Физика
15.03.2023 09:32
Просмотр содержимого документа
«Конспект урока по теме: "Равномерное движение по окружности"»
Тема: Равномерное движение по окружности
Цели урока:
Изучить равномерное движение тела по окружности и познакомить обучающихся с основными характеристиками данного движения.
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
К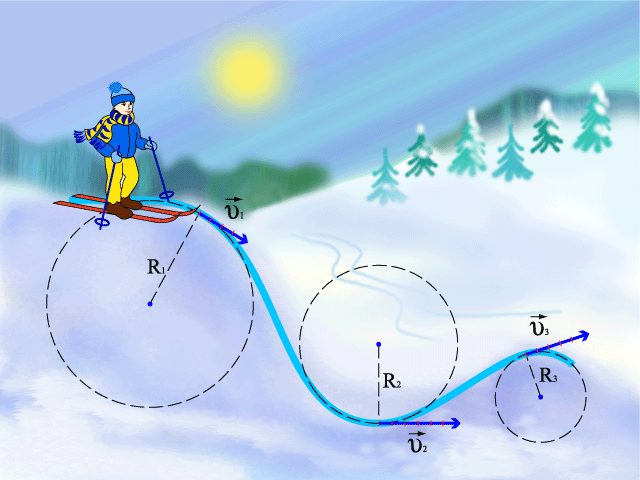
риволинейное движение в природе и технике более распространено, чем прямолинейное. Примеры: движение лыжника с горки на горку, движение человека на карусели, движение стержня ручки во время письма, движение частей станка при обработки детали (шлифование), полет волейбольного мяча после удара и тому подобное.
Любое криволинейное движение можно представить как последовательность движений по дугам окружностей различных радиусов.
1.Периодическое движение –это движение, повторяющееся через равные промежутки времени.
Рассмотрим частный случай криволинейного движения - движение по окружности, которое в окружающем мире распространено: движение стрелки часов, движение искусственных спутники Земли, зубчатые колесики в велосипеде; движение автомобиля и поезда на выпуклых мостах.
Д
вижение по окружности – это вращательное движение.
2.Вращательное движение- движение в одном направлений по плоской (или пространственной) замкнутой траектории(подобно движению Земли по орбите вокруг Солнца)
Н
арисуем окружность укажем в некоторых точках направление вектора мгновенной скорости.
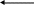
3. Мгновенная скорость тела, движущегося по окружности, направлена по касательной к ней в этой точке.
Наблюдая движение брызг грязи из-под колес автомобиля, что буксует мы в этом можем убедиться.
По касательной также разлетаются раскаленные частицы металла отрываются от стального резца, если коснуться им поверхности вращающегося точильного камня.
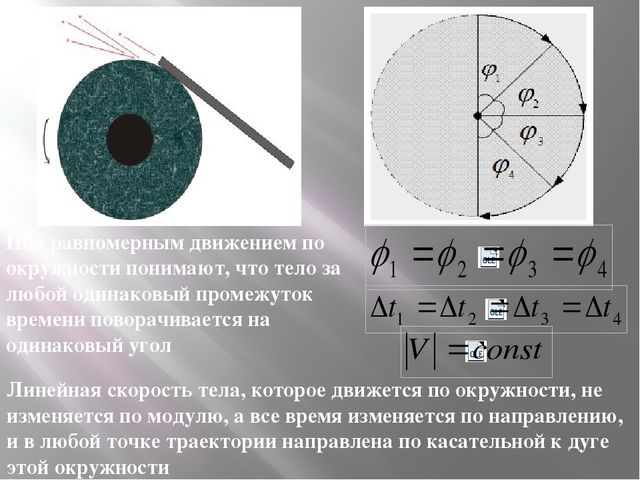
Мы будем изучать движение точки по окружности с постоянной по модулю скоростью. Его называют равномерным движением по окружности.
4. Равномерное движение по окружности - это движение тела по окружности, при котором модуль скорости тела остается постоянным.
5. Составим таблицу характеристик этого движения.
| Величина | обозначение | Единица измерения | Формула |
| Период | Т | с | Т=t/n; T=2πr/v |
| Частота | υ | Гц | υ =n/t=1/Т |
| Линейная скорость | v | м/с | v=2πr/T=ωr; v=Δl/Δt |
| Угловая скорость | ω | рад/с | ω=v/r=2π/T= Δφ/Δt |
| Ускорение | а | м/с2 | a=v2/r= ω2r |
1) Период вращения Т — это физическая величина, равная времени одного полного оборота.
Единица периода вращения в СИ — секунда ([Т] = с).
2) Частота вращения — это физическая величина, численно равна числу полных оборотов за единицу времени.
3) Линейная скорость v — это физическая величина, характеризующая криволинейное движение и равна отношению пути Δl, пройденного телом по криволинейной траектории за малый промежуток времени Δt, к величине этого промежутка. (Скорость точки, движущейся по окружности, называют линейной скоростью).
4) Угловая скорость — это физическая величина, равная отношению угла поворота радиуса, проведенного к телу от центра круга, по которому движется тело, к промежутку времени, в течение которого этот поворот осуществлялся.
5) Центростремительное ускорение – это ускорение, с которым тело движется по окружности с постоянной по модулю скоростью, всегда направлено вдоль радиуса окружности к центру.
6) Центростремительная сила – сила , действующая на тело при криволинейном движении в любой момент времени, всегда направлена вдоль радиуса к центру.
ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ У ДОСКИ
ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ У ДОСКИ
1. Кабинка карусели движется по окружности радиусом 24 м. Период его вращения равен 30с. Чему равна скорость движения кабинки?
Дано:
R=24м
Т=30с v=2πR/T v=2*π*24м /30с=48 π /30м/с=5 м/с
v-? Ответ: 5 м/с
Вопрос к классу
Чему равен период вращения часовой стрелки часов? минутной? секундной?
Тм=1ч=3600с;
Тс=1мин=60с;
Тч=12ч=12*3600с=43200с.
2. Во сколько раз скорость конца минутной стрелки башенных часов Биг-Бен в Лондоне больше скорости конца минутной стрелки наручных часов, если длина стрелки башенных часов — 4,2 м, а длина стрелки наручных часов — 1,5 см?
Справка. Часы на башне Биг-Бен в Лондоне до настоящего времени являются самыми большими в мире. Диаметр циферблата – 7 метров. Длина стрелок – 2,7 и 4,2 метра. Часовой механизм считается эталоном надежности, общий вес его составляет 5 тонн.
Дано:
Rб=4,2м Тмб = Тмр =1ч=3600с v=2πr/T
Rр=1,5 см = 1,5*10-2 м vб/ vб =(2*π*4,2м / 3600с/)*(3600с/2*π*1,5*10-2 м )=280 раз
vб/ vб -? Ответ: 280 раз
3.Напишите уравнение движения материальной точки, движущейся по дуге радиусом 5 м с угловой скоростью π/4 рад/с. Какими будут координаты точки через 3 с после начала отсчета времени?
Дано:
R=5м х=Rсоs ωt; y=Rsin ωt
ω= π/4 рад/с
х(t)-? х=5соs π/4t; y=5sin π/4t
y (t)-?
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ. РАБОТА ПО КАРТОЧКЕ.
Детская карусель за одну минуту совершает 4 оборота. Найти период и частоту, с которой она вращается.
Дано:
N=4об
T=1мин 60с Т=t/N T=60с/4=15с υ=N/t υ=4/60=1/15=0.067Гц
T-?
υ -? Ответ: 15 с,15 Гц
РЕФЛЕКСИЯ
Что нового узнали? Сложно ли использовать формулы при решении задач?
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
