Конспект урока
«Решение задач по теме неправильная пирамида и проекция ее вершины на плоскость основания »
Цель:
Образовательная – формирование навыков решения задач; формирование навыков построения высоты пирамиды; рассмотрение случаев расположения проекции вершин неправильной пирамиды.
Развивающая – развитие пространственного воображения, развитие общих приемов мыслительной деятельности; развитие логического мышления.
Воспитательная – воспитание аккуратности при выполнении чертежей, воспитание конструктивных умений, аргументированности, поиск решения в проблемной ситуации.
Задачи: 1. систематизировать знания по теме «Пирамида»,
2. закрепить навыки построения пирамид,
решение задач различного расположения проекции вершины в неправильной пирамиде.
УМК: «Геометрия 10-11» Л.С. Атанасян, В.Ф. Бутузов
Тип урока: комбинированный
Формы работы: групповая, индивидуальная.
Оборудование: модели пирамид, проектор.
План урока:
1) Организационный момент
2) Актуализация опорных знаний, создание проблемной ситуации
3) Этап подачи нового материала: рассмотрение случаев расположения проекции вершины неправильной пирамиды.
4) Этап усвоения материала и формирование умений и навыков: решение задач
5) Проведение контрольной работы.
Ход урока
І. Организационный момент:
Учитель: Здравствуйте, ребята. Сегодняшний урок мы начнем с того, что вспомним некоторые понятия, изученные ранее.
Актуализация опорных знаний.
Учитель: Посмотрите на слайд.
Из вершины В квадрата АВСD восстановлен перпендикуляр ВМ к его плоскости. Докажите, что АС перпендикулярно МО и МА перпендикулярно к AB (О – точка пересечения диагоналей).
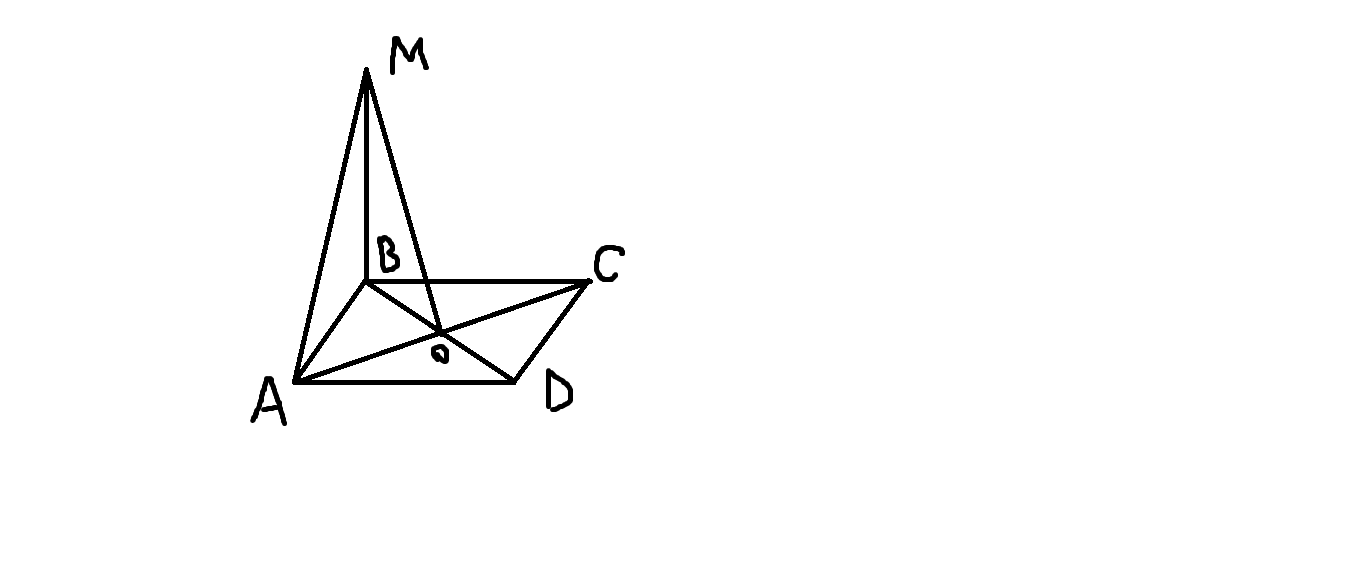
Учитель: Начнем с того, что докажем, что АС перпендикулярно МО. Кто знает как?
Спрашиваем устно ученика, поднявшего руку.
Ученик:
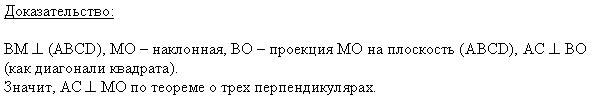
Учитель: Все правильно. Кто теперь сможет доказать, что АМ перпендикулярно к АВ?
Спрашиваем устно ученика, поднявшего руку.
Ученик:
BM ⊥ (ABCD), MA – наклонная, AO – проекция МА на плоскость (ABCD), BD ⊥ AC ( как диагонали квадрата). Значит MA ⊥ к AB.
-Учитель: Все правильно. Посмотрите на слайд.
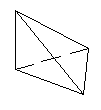
Среди изображенных фигур выберите номера тех фигур, которые являются неправильными пирамидами.




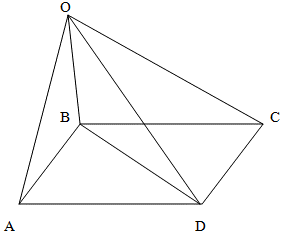
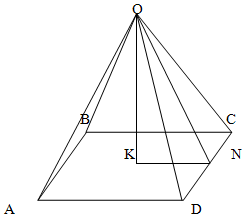
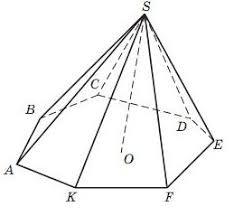
1 2 3


![]() 4
4 
5
Учитель: Дайте определение неправильной пирамиды?
Ученик: Пирамида называется неправильной, если её основанием является неправильный многоугольник или вершина проектируется не в центр основная.
Учитель сам выбирает, отвечающих. Одна буква – один ученик.
Учитель: Посмотрите на рисунок. Грань ADB перпендикулярна плоскости ABC. Куда будет проецироваться высота?
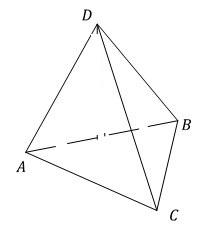
Ученик: Если 𝐷𝐴𝐵⊥𝐴𝐵𝐶, то точка 𝑂 принадлежит стороне AB.
Учитель: Посмотрите на слайд. Грани BDC и DBA перпендикулярны плоскости основания. Куда будет проецироваться высота?
Ученики: Если 𝐴𝐵𝐷⊥𝐴𝐵𝐶, 𝐵𝐷𝐶⊥𝐴𝐵𝐶, то вершина пирамиды проектируется в вершину основания В.
Мотивация
Учитель: на прошлом уроке мы решали задачи по теме неправильная пирамида и проекция ее вершины на плоскость основания. На этом уроке продолжим решать задачи.
Постановка учебной задач: решения задач.
Запишем тему урока - Тема урока «Решение задач»
2. Операционно-познавательная часть
Учитель: Посмотрите на слайд. Давайте решим эту задачу.
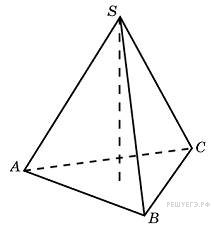
Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенуза AB равна 29 см, катет AC равен 21 см. Ребро DA перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
Учитель: Сделаем рисунок к задаче:

Учитель: Можно ли эту задачу отнести к какому-нибудь типу из нашей таблицы ключевых задач?
Ученик: Да, к 6.
Учитель: Значит куда будет проецироваться высота?
Ученик: В вершину А.
Учитель: Как мы сможем найти площадь боковой поверхности?
Ученик: Площадь боковой поверхности будет равна сумме площадей треугольников: DAC, DCB, ADB.
Учитель: Как мы найдем площадь треугольника DAC?
Ученик: (AD * AC) / 2
Учитель: Как мы найдем площадь треугольника ADB?
Ученик: (AD * DB) / 2
Учитель: Как мы найдем площадь треугольника DCB?
Ученик: (DC * CB) / 2
Учитель: По этой формуле находится площадь прямоугольного треугольника. Треугольник DCB будет прямоугольным?
Ученик: да, т.к. по теореме о трех перпендикулярах DC будет перпендикулярно CB.
Учитель: Хорошо. А как мы найдем CB и DC?
Ученик: По теореме Пифагора из треугольников АВС и АDC.
Учитель: Хорошо. Выйди к доске и запиши решение.
Вызываем одного ученика к доске.
Решение:
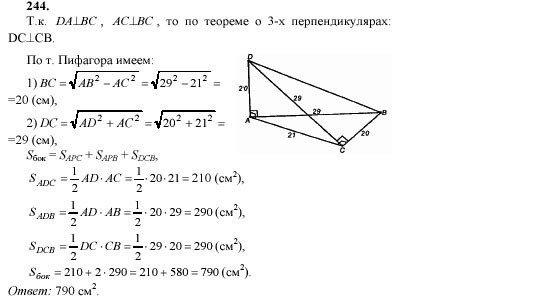
-Учитель: Посмотрите на слайд. Давайте решим эту задачу.
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 12. Найдите площадь основания пирамиды.

-Cкажите куда будет проецироваться точка S? Почему?
-На сторону AD, по свойству пирамиды, где одна боковая грань перпендикулярна плоскости основания.
-Скажите, чему будут равны линейные углы двугранных углов SAD и SDA в треугольнике?
-60 градусам
-Gочему?
- По теореме о 3х перпендикулярах AB перп. AD, а если AB перп. Проекц., то и перп. и самой наклонной тогда SA перп. AB следовательно SAD и SDA линейные углы двугранных углов и равны 60 градусов
-А чему равен угол ASD
-ASD равен 60 градусам, а следовательно треугольник SAD равносторонний
-Остался еще один угол, какой?
-Угол между плоскостью основания и треугольником SCB.
-Правильно давайте его обозначим, опустив высоту SG и соединив с H. Чем будет являться HG?
-Проекцией SG на плоскость основания, а также будет параллелен AB, DC тк ABCD-прямоугольник.
-что мы можем найти из треугольника ASD?
-Сторону, треугольник — равносторонний, а его сторона связана с высотой формулой  откуда
откуда 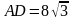
Из прямоугольного треугольника SHG находим:

Поскольку ABCD — прямоугольник, его площадь равна произведения сторон:
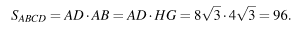
Учитель: А теперь мы напишем контрольную работу.
Учитель раздает контрольную работу (два варианта)
Вариант 1:
-
В основании пирамиды лежит равносторонний треугольник. Будет ли эта пирамида правильной?
 Да, если вершина проецируется в центр основания.
Да, если вершина проецируется в центр основания.
Нет, не будет.
-
Одна боковая грань пирамиды перпендикулярна плоскости
основания, тогда точка 𝑂 принадлежит стороне основания если ________________
-
Выберите 3 верных утверждения для пирамиды, где все боковые ребра образуют равные углы со смежными сторонами основания:
-
Высоты боковых граней, проведенные из вершины пирамиды, равны.
-
Боковые ребра пирамиды равно наклонены к высоте пирамиды.
-
Расстояния от проекций вершины пирамиды на плоскость основания до смежных ребер основания равны.
-
Проекции боковых ребер на плоскость основания равны.
-
Боковые грани пирамиды равно наклонены к плоскости основания
-
Все боковые ребра пирамиды равны. Обозначьте центр вписанной окружности - точку О, если 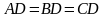 .
.

точка  на данном рисунке - будет точкой
на данном рисунке - будет точкой
пересечения _____________________
Вариант 2
-
В основании пирамиды лежит квадрат. Может ли эта пирамида быть неправильной?
Да, если вершина не проецируется в центр основания

Нет, не может
-
Две смежные боковые грани пирамиды перпендикулярны, тогда если 𝐴𝐵𝐷⊥𝐴𝐵𝐶, 𝐵𝐷𝐶⊥𝐴𝐵𝐶, вершина пирамиды проектируется в _________________
-
Выберите 3 верных утверждения для пирамиды, где все боковые ребра пирамиды равны:
-
Высоты боковых граней, проведенные из вершины пирамиды, равны.
-
Проекции боковых ребер на плоскость основания равны.
-
Боковые ребра пирамиды равно наклонены к высоте пирамиды.
-
Боковые ребра пирамиды равно наклонены к плоскости основания.
-
Проекции двух равных ребер пирамиды на плоскость основания равны.
-
Все боковые ребра пирамиды образуют равные углы со смежными сторонами основания. Обозначьте центр вписанной окружности - точку О, если ∠𝐷𝐴𝐵=∠𝐷𝐴𝐶=∠𝐷𝐶𝐴=∠𝐷𝐶𝐵=∠𝐷𝐵𝐶=∠𝐷𝐵𝐴
точка  – точка пересечения __________________
– точка пересечения __________________
Ответы на тест:
Вариант 1
-
Да, если вершина проецируется в центр основания.
-
𝐷𝐴𝐵⊥𝐴𝐵𝐶
-
Проекции боковых ребер на плоскость основания равны.
Боковые ребра пирамиды равно наклонены к высоте пирамиды.
Боковые ребра пирамиды равно наклонены к плоскости основания.
-
биссектрис
Вариант 2
-
Да, если вершина не проецируется в центр основания
-
Одну из вершин основания
-
Высоты боковых граней, проведенные из вершины пирамиды, равны.
Расстояния от проекций вершины пирамиды на плоскость основания до смежных ребер основания равны.
Боковые грани пирамиды равно наклонены к плоскости основания
-
серединных перпендикуляров
Записи в тетради
Классная работа
Тема урока «Решение задач»
Задача 1.

Задача 2.
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 12. Найдите площадь основания пирамиды.

Решение:
Поскольку боковые грани SAB, SDC и SBC наклонены к основани. под углом 60°, углы A и D в треугольнике ASD и угол G в треугольнике SGH равны 60°.
Поэтому треугольник ASD — равносторонний, а его сторона связана с высотой формулой  откуда
откуда 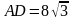 Из прямоугольного треугольника SHG находим:
Из прямоугольного треугольника SHG находим:

Поскольку ABCD — прямоугольник, его площадь равна произведения сторон:
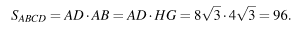
Ответ:96







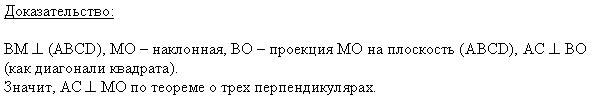
















 откуда
откуда 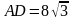
 Да, если вершина проецируется в центр основания.
Да, если вершина проецируется в центр основания.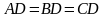 .
.

















