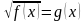9
Правительство Свердловской области
Министерство общего и профессионального образования
Свердловской области
Государственное образовательное учреждение дополнительного профессионального образования Свердловской области
«Институт развития образования»
(ГБОУ ДПО СО «ИРО»)
Кафедра естественнонаучного и математического образования
Проект конструкта занятий по математике с педагогами
ОП «Обучение тьюторов для подготовки педагогов к проведению ЕГЭ по математике» (108 час.)
Колупаева Наталья Анатольевна
Муниципальное автономное общеобразовательное
учреждение средняя общеобразовательная школа №2
г.Карпинск, Свердловская область
г. Екатеринбург 2012г.
СОДЕРЖАНИЕ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ОСНОВНАЯ ЧАСТЬ
Анализ школьных учебников по алгебре и началам
анализа…………………………………………………………………5
«Алгебра,9»……………………………………………………………5
«Алгебра и начала анализа, 10-11» ………………………………….6
1.3. «Алгебра и начала анализа, 10» …………………………………6
Методы решения иррациональных уравнений.
Решение иррациональных уравнений методом возведения обеих
частей в одну и ту же степень. Уравнения вида 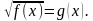
Уравнения вида  =
= ……………………………………..7
……………………………………..7
Решение иррациональных уравнений методом введения
новой переменной. ………………………………………………………..8
Сведение решения иррационального уравнения к решению тригонометрического уравнения……………………………………………8
Решение иррациональных уравнений с использованием свойств
входящих в них функций……………………………………………………9
Метод мажорант…………………………………………………………9
Конструкт занятия……………………………………………...10
ЗАКЛЮЧЕНИЕ………………………………………………………..14
СПИСОК ЛИТЕРАТУРЫ……………………………………………15
ПРИЛОЖЕНИЯ………………………………………………………..16
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Уравнения сами по себе представляют интерес для изучения, так как именно с их помощью на символическом языке записываются важнейшие задачи познания реальной действительности. Умение решать уравнения различных видов – одно из основных требований, предъявляемых к выпускникам средней школы.
Одним из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные уравнения, так как в школе им уделяют достаточно мало внимания.
Трудности при изучении данного вида уравнений, связаны со следующими их особенностями:
1) в большинстве случаев учащиеся не успевают за время, отведенное на изучение данной темы, нарабатывать четкий алгоритм решения иррациональных уравнений;
2) при решении уравнений часто приходится делать преобразования, вследствие чего возникают ошибки, которые обычно связаны с потерей или приобретением посторонних корней в процессе решения.
Опыт показывает, что учащиеся в недостаточной степени овладевают умением решать иррациональные уравнения, часто допускают ошибки при их решении. А ведь иррациональные уравнения встречаются достаточно часто и в вступительных работах в ВУЗы, и в текстах заданий ЕГЭ (задание В3на ЕГЭ до 2012 года и задание В5 с 2012 года, а иногда в заданиях С1 и С3). Анализ выполнения задания В3 показывает, что в 2010 году с этим заданием справились 81, 4% учащихся в РФ и 79,4% в СО, а в 2011 – 88%. И даже не все учащиеся (99%) с высоким уровнем подготовки по математике справились с этим заданием. Для успешного выполнения заданий группы С недостаточно знать стандартные (предлагаемые в современных школьных учебниках) способы решения уравнений с радикалами. Поэтому на отработку традиционных, нетрадиционных и оригинальных методов решения иррациональных уравнений стоит обратить особое внимание.
Выше изложенное обусловливает и актуальность темы исследования.
Гипотеза исследования: освоение умения различать основные виды иррациональных уравнений, умения применять необходимые приемы и методы их решения позволит учащимся решать иррациональные уравнения на сознательной основе, выбирать наиболее рациональные способы решения, в том числе те, которые не рассмотрены в школьных учебниках.
Цель:
рассмотреть основные виды иррациональных уравнений, изучить методы их решения и на основе этого сформулировать методические рекомендации для подготовки и проведения факультативных занятий по данной теме в рамках подготовки к ЕГЭ по математике.
Задачи:
проанализировать действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений;
изучить стандарты образования и учебно-методическую литературу по данной теме;
подобрать примеры решения иррациональных уравнений для демонстрации излагаемой теории.
Объект исследования:
Составление конструкта занятий по теме «Иррациональные уравнения»
Предмет исследования:
Методы решения иррациональных уравнений
Методы исследования:
Планируемый результат:
Повышение профессиональной компетентности учителя
ОСНОВНАЯ ЧАСТЬ
1. Анализ школьных учебников по алгебре и началам анализа.
При изучении любой новой темы в основном курсе школы встает проблема изложения данной темы в школьных учебниках. Пропедевтикой изучения раздела иррациональных уравнений в школе является введение понятие арифметического корня и, соответственно, рассмотрение его свойств.
Проанализируем в каких классах вводится данное понятие разными авторами учебников. Алимов Ш. А. в учебнике «Алгебра. 9класс» вводит понятие арифметического корня натуральной степени, а также свойства арифметического корня. Макарычев Н. Г. же разделяет понятия квадратного корня и корня 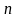 -ой степени. В учебнике «Алгебра. 8 класс» вводится понятие арифметического квадратного корня и, соответственно, рассматриваются его свойства. В учебнике «Алгебра. 9 класс» вводятся понятия корня
-ой степени. В учебнике «Алгебра. 8 класс» вводится понятие арифметического квадратного корня и, соответственно, рассматриваются его свойства. В учебнике «Алгебра. 9 класс» вводятся понятия корня 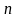 -ой степени, арифметического корня
-ой степени, арифметического корня 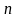 -ой степени и рассматриваются свойства арифметического корня
-ой степени и рассматриваются свойства арифметического корня 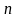 -ой степени. Колмогоров А. Н. в учебнике «Алгебра. 10 класс» вводит понятия корня
-ой степени. Колмогоров А. Н. в учебнике «Алгебра. 10 класс» вводит понятия корня 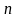 -ой степени, арифметического корня
-ой степени, арифметического корня 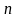 -ой степени и рассматривает свойства арифметического корня
-ой степени и рассматривает свойства арифметического корня 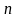 -ой степени перед изучением иррациональных уравнений. Мордкович А. Г. в учебнике «Алгебра. 8 класс» вводит понятие квадратного корня и его свойства. Кроме того, в этом же учебнике есть отдельный параграф, посвященный иррациональным уравнениям.
-ой степени перед изучением иррациональных уравнений. Мордкович А. Г. в учебнике «Алгебра. 8 класс» вводит понятие квадратного корня и его свойства. Кроме того, в этом же учебнике есть отдельный параграф, посвященный иррациональным уравнениям.
1.1. «Алгебра, 9», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.[1].
Материал по данной теме изложен в III главе «Степенная функция», параграфа «Неравенства и уравнения, содержащие степень». В параграфе дается понятие иррационального уравнения, приводится несколько примеров простейших иррациональных уравнений вида 
 , которые решаются с помощью возведения обеих частей уравнения в квадрат. Отмечается, что при возведении обеих частей уравнения в квадрат могут появиться посторонние корни и поэтому необходимо делать проверку.
, которые решаются с помощью возведения обеих частей уравнения в квадрат. Отмечается, что при возведении обеих частей уравнения в квадрат могут появиться посторонние корни и поэтому необходимо делать проверку.
После пункта приведены упражнения для закрепления умений решать иррациональные уравнения. В №№195-199 предложены простейшие уравнения вида  а в №№202-204 более сложные, решить которые можно с помощью возведения обеих частей уравнения в квадрат.
а в №№202-204 более сложные, решить которые можно с помощью возведения обеих частей уравнения в квадрат.
1.2. «Алгебра и начала анализа, 10-11», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. [2].
В данном учебнике нет материала, посвященного иррациональным уравнениям. Лишь в конце учебника помещены упражнения для итогового повторения курса алгебры. Здесь есть только один номер для решения простейших иррациональных уравнений (№801). Это можно объяснить тем, что тема «Иррациональные уравнения» изучалась в 9 классе, а умение решать иррациональные уравнения не является обязательным для учащихся и соответствующая тема может быть предложена для изучения самостоятельно или на факультативных занятиях. [2] Поэтому в учебнике предложены задачи для внеклассной работы, где встречаются иррациональные уравнения (№№934, 947).
1.3. «Алгебра и начала анализа, 10», авт. Ю.М.Колягин и др.[3].
Материал по данной теме изложен в III главе «Степенная функция», параграфа «Иррациональные уравнения». В параграфе дается понятие иррационального уравнения, приводится несколько примеров простейших иррациональных уравнений вида 
 , которые решаются с помощью возведения обеих частей уравнения в квадрат. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Показано, что кроме возведения в квадрат иррациональные уравнения можно решать графически. Рассмотрен пример иррационального уравнения, содержащего корень третьей степени. Для того чтобы «избавиться от радикала», обе части такого уравнения возводятся в куб.
, которые решаются с помощью возведения обеих частей уравнения в квадрат. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Показано, что кроме возведения в квадрат иррациональные уравнения можно решать графически. Рассмотрен пример иррационального уравнения, содержащего корень третьей степени. Для того чтобы «избавиться от радикала», обе части такого уравнения возводятся в куб.
После пункта приведены упражнения для закрепления умений решать иррациональные уравнения. В №№230-235 предложены простейшие уравнения вида 
 , решить которые можно с помощью возведения обеих частей уравнения либо в квадрат, либо в куб, либо в четвертую степень. Такие задачи, по мнению авторов учебника необходимо уметь решать для получения удовлетворительной оценки. Задачи же в №№236-241 чуть сложнее. И в №№242-243 приведены уравнения повышенной сложности.
, решить которые можно с помощью возведения обеих частей уравнения либо в квадрат, либо в куб, либо в четвертую степень. Такие задачи, по мнению авторов учебника необходимо уметь решать для получения удовлетворительной оценки. Задачи же в №№236-241 чуть сложнее. И в №№242-243 приведены уравнения повышенной сложности.
2. Методы решения иррациональных уравнений.
2.1 Решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень. Уравнения вида 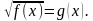
Рассмотрим уравнение вида 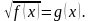
В ОДЗ левая часть уравнения всегда неотрицательна – поэтому решение может существовать только тогда, когда  . В этом случае обе части уравнения неотрицательны, и возведение в квадрат дает равносильное в ОДЗ уравнение.
. В этом случае обе части уравнения неотрицательны, и возведение в квадрат дает равносильное в ОДЗ уравнение.
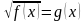


Уравнения вида  =
=
Пусть задано уравнение  =
=
В ОДЗ обе части неотрицательны, и возведение в квадрат дает равносильное уравнение  . Поэтому
. Поэтому
 =
=

 =
=

При таком способе решения достаточно проверить неотрицательность одной из функций – можно выбрать более простую.
2.2 Решение иррациональных уравнений методом введения новой переменной.
Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной. Поэтому не стоит при решении уравнений торопиться начинать преобразования. Стоит посмотреть, нельзя ли записать уравнение проще, введя новую переменную. Новая переменная в уравнениях иногда действительно очевидна, иногда несколько завуалирована, но «ощущается». Случается, что ее можно выявить лишь в процессе преобразований. Иногда полезно ввести не одну, а две новые переменные.
Уравнения вида:
A
2.3 Сведение решения иррационального уравнения к решению тригонометрического уравнения.
Заменой неизвестной решение иррациональных уравнений иногда можно свести к решению тригонометрических уравнений. При этом полезными могут оказаться следующие замены неизвестной.
Если в уравнение входит радикал  , то можно сделать замену х=аsint или х=accost.
, то можно сделать замену х=аsint или х=accost.
Если в уравнение входит радикал  , то можно сделать замену x=atgt.
, то можно сделать замену x=atgt.
Если в уравнение входит радикал  , то можно сделать замену x=
, то можно сделать замену x=  или x=
или x= .
.
2.4 Решение иррациональных уравнений с использованием свойств входящих в них функций.
Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решение уравнения непосредственной подстановкой чисел из ОДЗ.
2.5 Метод мажорант.
1.Мажорантой данной функции  на заданном промежутке называется такое число М, что либо
на заданном промежутке называется такое число М, что либо  для всех х из данного промежутка, либо
для всех х из данного промежутка, либо  для всех х из данного промежутка.
для всех х из данного промежутка.
2. Основная идея метода мажорант состоит в следующем. Пусть мы имеем уравнение  (1), и существует такое М, что для любого х из ООУ имеем
(1), и существует такое М, что для любого х из ООУ имеем  и
и  (или наоборот). Тогда уравнение (1) равносильно системе
(или наоборот). Тогда уравнение (1) равносильно системе
3. Опорные неравенства.
1. а)  при
при  равенство при
равенство при 
б)  при
при  равенство достигается при
равенство достигается при 
2.  при
при  равенство достигается при
равенство достигается при 
3. .
Признаки присутствия мажоранты в задаче
Смешанное уравнение (или неравенство), т.е. в задании есть разнородные функции, например, логарифмическая и линейная, или квадратный трехчлен и тригонометрическая, или вообще несколько видов.
Сложный, трехэтажный и пугающий вид, большие числа и коэффициенты.
Конструкт занятия
Тема: «Иррациональные уравнения и методы их решения»
Цель занятия: расширить представление о методах решения иррациональных уравнений
Задачи занятия: повторить традиционные методы решения иррациональных уравнений, овладеть нетрадиционными и оригинальными методами решения иррациональных уравнений.
Учебное оборудование
учебное пособие “Алгебра и начала анализа. 10», авт. Ю.М.Колягин и др,
тетрадь,
авторучка,
мультимедиа проектор,
компьютер,
презентация.
Дидактический материал
Технологическая карта занятия
| Этапы занятия | Цель | Содержание учебного материала | Деятельность учителя | Деятельность обучающихся | Показатели результатов
|
| Организационный | Формулирование цели занятия, составление плана по достижению цели. |
| Помогает обучающимся сформулировать цель занятия, знакомит с планом деятельности.
| Формулируют цель, выдвигают гипотезу по ее достижению, обсуждают план действий. | Готовность к сотрудничеству. |
| Мотивационный | Сформировать потребность в овладении учебным материалом: показать значимость материала для успешной сдачи учащимися ЕГЭ. | Знакомство с темами занятий
| Нацеливает на освоение новых методов и приемов с позиции их практической значимости.
| Осмысливают значимость предлагаемого к изучению материала, соотнося имеющиеся знания. | Включение в работу. |
| Применение знаний в новой ситуации
Уравнения вида
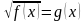
и  = =
| Реализация плана действий.
Отработать умение решать простейшие иррациональные уравнения данного вида
|
Определение иррационального уравнения, решение простейших иррациональных уравнений, методом возведения обеих частей уравнения в одну и ту же степень с последующей проверкой полученных корней, а также методом сведения к равносильной системе уравнений. Метод уединения радикала. | Предъявляет требования к учебной деятельности, направляет деятельность: 1.Фронтальная работа; 2.Индивидуальная работа с заданиями для самостоятельной работы.
| Выполняют действия направленные на решения поставленной учебной задачи: - решают уравнения; -участвуют в обсуждении хода решения; -сравнивают с другими способами и методами решения.
| Выполнение заданий для самостоятельного решения. |
| Решение иррациональных уравнений методом введения новой переменной.
| Рассмотреть способы решения иррациональных уравнений методом замены переменной | Применение метода замены в случае, если в уравнении неоднократно встречается некоторое выражение. Решение иррациональных уравнений методом сведения к эквивалентным системам рациональных уравнений при помощи введения двух вспомогательных неизвестных.
| Знакомит с подборкой заданий по данной теме, разбирает случаи, когда учащиеся могут допустить ошибки. (приложение 2) | Участвуют в обсуждении хода решения уравнения, предлагают свои методы.
| Выполнение заданий для самостоятельного решения. |
| Применение рационализирующих подстановок при решении иррациональных уравнений | Рассмотреть способы сведения иррациональных уравнений к решению тригонометрических уравнений | Рассмотрение рационализации некоторых выражений, содержащих радикалы, с помощью рационализирующих подстановок и применение этих подстановок при решении иррациональных уравнений.
| Знакомит с теоретическим материалом по данной теме (приложение 3) | Обсуждение хода решения. | Выполнение заданий для самостоятельного решения. |
| Решение иррациональных уравнений с использованием свойств входящих в них функций.
| Показать способы решения иррациональных уравнений, используя свойства входящих в них функций. | Использование ОДЗ, монотонности, графиков функций при решении иррациональных уравнений.
| Знакомит с подборкой заданий по данной теме (приложение 4) |
| Выполнение заданий для самостоятельного решения. |
| Использование метода мажорант. | Познакомить с методом и показать, что он почти всегда встречается в вузовских олимпиадах и в некоторых заданиях С на ЕГЭ. | В методе мажорант надо хорошо понимать, что такое функция, уметь исследовать свойства функции и знать некоторые нестандартные неравенства. | Рассматривает примеры применения данного метода (приложение 5) | Участвуют в обсуждении и работают с приложением. | Решают уравнения, применяя новые методы. |
| Контрольный | Проверить правильность решения поставленной задачи и оценить степень достижения цели. |
| Оценивает результаты деятельности обучающихся. | Коллективно дают оценку, обмениваются мнениями о правильности выполнения учебной задачи. | Подборка примеров для использования на факультативных занятиях |
| Рефлексивный | Проанализировать пути решения учебной задачи. |
| Ставит вопросы о том, как решались задачи и достигалась цель занятия. Анализирует уровень освоенности новых методов. | Формулируют выводы по теме занятия, определяют значимость полученных знаний. | Удовлетворенность работой |
Заключение
В данной работе рассмотрена методика обучения решению иррациональных уравнений в школе.
При проведении исследования были решены следующие задачи:
1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы:
• в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном программой предусмотрено формирование у учащихся умение решать простейшие иррациональные уравнения;
• в учебнике [2] материала, посвященного методам решения иррациональных уравнений нет. В остальных учебниках рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных преобразований;
• среди предлагаемых заданий в учебниках много однотипных;
2) Изучена учебно-методическая литература по данной теме;
3) Рассмотрены основные методы и приемы решения различных иррациональных уравнений традиционными, нетрадиционными и оригинальными способами;
4) Рассмотрены ситуации, связанные с потерей или приобретением посторонних корней в процессе решения, показано, как распознавать и предотвращать их;
5) Подобраны примеры решения иррациональных уравнений для демонстрации излагаемого теоретического материала и для использования на факультативных занятиях по подготовке к ЕГЭ;
6) Разработан конструкт занятия.
СПИСОК ЛИТЕРАТУРЫ
Открытый банк заданий ЕГЭ 2012. Режим доступа:[ http://mathege.ru]
Методы решения иррациональных уравнений. Режим доступа:[ http://www.proshkolu.ru/]
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра 9 – М.: Просвещение, 2002.-255 с.
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра начала анализа 10-11 – М.: Просвещение, 2002.-254 с.
Колягин Ю.М. и др. Алгебра и начала анализа 10 – М.: Мнемозина, 2001.-364 с.
Самсонов П.И. Четыре месяца до выпускного экзамена – М.: Школьная Пресса, 2003.-80с.
Олехник С.Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10-11 классы – М.:Дрофа,2001.-192с.
Мордкович А.Г. Беседы с учителями математики. _ М.:ООО «Издательство «Мир и образование», 2008.-336с.
Письменный Д.Т. Готовимся к экзамену по математике – М.: Айрис-пресс, 2006.-352с.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1.
Задача 1. Решить уравнение 
Решение.




 х=1.
х=1.
Ответ.1
Комментарии
Сначала обратим внимание на то, что запись решения задачи с использованием равносильных переходов наиболее полно и емко отражает все этапы решения данной задачи и не требует никаких словесных пояснений.
Заметим, что условие корректности операции возведения в квадрат записывается по правой части уравнения, а не по подкоренному выражению, как ошибочно записывают ученики.
Квадратное уравнение  решается подбором корней (используется теорема, обратная теореме Виета), поэтому специально приводить решение этого уравнения не нужно.
решается подбором корней (используется теорема, обратная теореме Виета), поэтому специально приводить решение этого уравнения не нужно.
Как быть, если ученик не владеет методом равносильных переходов? Приведем пример оформления решения этой задачи в такой ситуации.
Решение.
 ,
,  . Возведем обе части уравнения в квадрат
. Возведем обе части уравнения в квадрат

х=1: Полученное числовое равенство является верным, значит, х=1-корень данного уравнения.
Полученное числовое равенство является верным, значит, х=1-корень данного уравнения.
х
1. 
D=36-28=8,  =
=

2. Сравним числа 
Так как 2 , то в силу возрастания функции у= ,
, то в силу возрастания функции у= , 
=-2:  Полученное числовое равенство является неверным, значит, х=-2 корнем данного уравнения не является.
Полученное числовое равенство является неверным, значит, х=-2 корнем данного уравнения не является.
Ответ.1
Задача 2. Решите уравнение  3х-5
3х-5
Решение.
 3х-5
3х-5
 х=3+
х=3+
Ответ. 3+
Комментарии
Особенность этой задачи заключалось в том, что в процессе ее решения необходимо было сравнить число Такое сравнение, в отличие от первой задачи, далеко не очевидно, поэтому справа от решения это сравнение рассмотрено отдельно.
Отметим также, что использовать для сравнения таких «близких» чисел калькулятор нельзя.
Обратить внимание, что в совокупности у переменной х нет никаких индексов.
Задача 3. Решите уравнение
Решение.



 х=
х=
 х=-2.
х=-2.
Ответ.-2
Комментарий
Так как выражение  +1 принимает при любом х только положительные значения, то при возведении в квадрат никаких дополнительных условий записывать не нужно.
+1 принимает при любом х только положительные значения, то при возведении в квадрат никаких дополнительных условий записывать не нужно.
Задача 4. Решите уравнение 
Решение.








 х=8-2
х=8-2






 х=2.
х=2.




Ответ.  и 2.
и 2.
Задания для самостоятельного решения.
 (Ответ.1)
(Ответ.1)
(Ответ.1)
(Ответ.2)
(Ответ.-2)
 +
+  (Ответ.4,25)
(Ответ.4,25)
и в ответе укажите те из них, которые являются корнями уравнения ( . (Ответ. 3)
. (Ответ. 3)
ПРИЛОЖЕНИЕ 2.
Задача1. Решите уравнение .
Решение.
 2
2  2
2
Пусть t = Тогда t2=2х2-6х+5, и поэтому t2-4t-5=0 

Значит t=5. Поэтому
 =5
=5  2
2
 2
2 -6х-20=0
-6х-20=0 

 х1=-2, х2=5.
х1=-2, х2=5.
Ответ. -2;5.
Комментарий
Это хорошо известный вид иррациональных уравнений, который в общем виде выглядит так: А(ах2+bx+c)+B при составлении таких уравнений раскрывают скобки в А(ах2+bx+c), часть слагаемых переносят в другую часть уравнения и т.п. Решение, грубо говоря, состоит в обратном восстановлении этих преобразований и основано на введении новой переменной t = .
.
Задача 2. Решите уравнение  =4.
=4.
Решение.
 =4, ,
=4, ,
Пусть .
 , D=4+32=36,
, D=4+32=36,  ,
,
t1=2, t2=-4(не удовлетворяет условию 
Обратная замена: , по определению логарифма х=81.
Ответ.81
Задача 3. Решить уравнение  (*)
(*)
Решение. Возведя обе части уравнения (*) в квадрат, получим уравнение
(**)
являющееся следствием уравнения (*). Если возведем в квадрат уравнение (**), то получим уравнение
112-32 (***)
являющееся следствием уравнения (**).
Сделав замену неизвестной =t, уравнение (***) перепишем в виде t2-32t+112=0. Решения этого уравнения t1=4, t2=28. Следовательно имеем совокупность уравнений
и , являющуюся следствием исходного уравнения (*). Первое уравнение из совокупности имеет единственное решение х1=1. Второе уравнение этой совокупности решений не имеет. Следовательно, совокупность имеет единственное решение х=1. Проверкой убеждаемся, что х=1 – корень уравнения.
Ответ. 1.
Задача 4. Решить уравнение
Решение. Заметив, что
введем две новые переменные . Тогда уравнение примет вид a+b=3х-16+2ab.
Осталось установить, как выразить 3х через a и b. Замечаем, что a2=2x+3, b2=x+1. Значит, a2+b2=3x+4, 3x=a2+b2-4 и уравнение можно переписать
a+b=(a2+b2-4)-16+2ab, (a+b)2-(a+b)-20=0.
Введем еще одну новую переменную: a+b=y. Получим уравнение y2-y-20=0 с корнями y1=5, y2=-4. Следовательно, a+b=5; a+b=-4, или

 второе уравнение не имеет корней, а из первого находим: х=3.
второе уравнение не имеет корней, а из первого находим: х=3.
Ответ. 3.
Задания для самостоятельного решения.
5 Ответ. (9)
Ответ. (9)
 (Ответ. х1,2=1 )
(Ответ. х1,2=1 )
(Ответ. 4; -61)
 (Ответ.
(Ответ. 
ПРИЛОЖЕНИЕ 3.
Задача 1. Решить уравнение 
Решение.
ОДЗ: х .
.
Пусть х=tgt, где  Тогда уравнение примет вид
Тогда уравнение примет вид  - tgt =
- tgt =  cost. Поскольку cost
cost. Поскольку cost для рассматриваемых t, то уравнение для этих t равносильно уравнению 2-2sint=5(1-sin2t). А это уравнение равносильно совокупности уравнений sint=1 и sint=-
для рассматриваемых t, то уравнение для этих t равносильно уравнению 2-2sint=5(1-sin2t). А это уравнение равносильно совокупности уравнений sint=1 и sint=-
Из решений этих уравнений промежутку  принадлежит только t=arcsin(
принадлежит только t=arcsin(
Обратная замена х=tg arcsin(- )=
)=
Ответ.
Задания для самостоятельного решения.
х+ (Ответ.
(Ответ.  )
)
 (Ответ. )
(Ответ. )
ПРИЛОЖЕНИЕ 4.
Задача1. Решить уравнение
Решение. ОДЗ:  . Этим решение уравнения и завершается, так как установлено, что ни одно число не может являться решением, т.е. что уравнение не имеет корней.
. Этим решение уравнения и завершается, так как установлено, что ни одно число не может являться решением, т.е. что уравнение не имеет корней.
Ответ. решений нет.
Задача 2. Решить уравнение
Решение. ОДЗ: 
Подставляя эти значения х в исходное уравнение получаем, что его левая и правая части равны 0, а это означает, что все , являются его решениями.
, являются его решениями.
Ответ. 
Задача 3. Решить уравнение
Решение.
Рассмотрим функцию у= , D(y)=[0; + /
/
Эта функция монотонно возрастает, как сумма возрастающих функций. Найдем подбором корень, х=1. В силу теоремы о корне, имеем, что он единственный.
Ответ.1.
Задания для самостоятельного решения.
(Ответ. решений нет)
 (Ответ. решений нет)
(Ответ. решений нет)
 (Ответ. решений нет)
(Ответ. решений нет)
(Ответ. 1)
ПРИЛОЖЕНИЕ 5.
Задача. Решить уравнение .
Решение. Так как левая часть уравнения неотрицательна, как сумма двух неотрицательных значений, то и правая часть неотрицательна.
3-5х2 .
Оценим левую часть уравнения:
 ,
,  , а значит
, а значит
Оценим правую часть уравнения:
3-5х2
Следовательно, левая часть исходного уравнения может быть равна правой части, только если обе части равны одновременно 3. Правая часть уравнения равна 3 только при х=0. Подставив это значение в левую часть, убеждаемся, что это и есть корень уравнения.
Ответ.0.







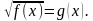
 =
= ……………………………………..7
……………………………………..7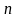 -ой степени. В учебнике «Алгебра. 8 класс» вводится понятие арифметического квадратного корня и, соответственно, рассматриваются его свойства. В учебнике «Алгебра. 9 класс» вводятся понятия корня
-ой степени. В учебнике «Алгебра. 8 класс» вводится понятие арифметического квадратного корня и, соответственно, рассматриваются его свойства. В учебнике «Алгебра. 9 класс» вводятся понятия корня 
 , которые решаются с помощью возведения обеих частей уравнения в квадрат. Отмечается, что при возведении обеих частей уравнения в квадрат могут появиться посторонние корни и поэтому необходимо делать проверку.
, которые решаются с помощью возведения обеих частей уравнения в квадрат. Отмечается, что при возведении обеих частей уравнения в квадрат могут появиться посторонние корни и поэтому необходимо делать проверку.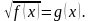
 . В этом случае обе части уравнения неотрицательны, и возведение в квадрат дает равносильное в ОДЗ уравнение.
. В этом случае обе части уравнения неотрицательны, и возведение в квадрат дает равносильное в ОДЗ уравнение.