Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 1
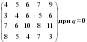 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
В офисе 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с 5 другими? Может ли в офисе, в котором каждый телефон соединен ровно с 5 другими, быть ровно 16 телефонов?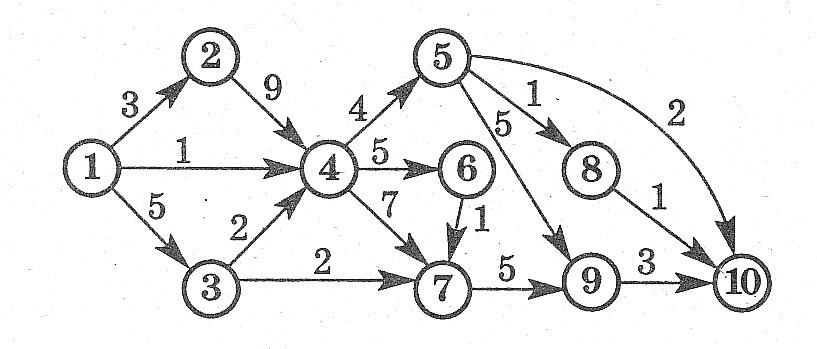
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена?
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 250 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 50 тыс. долл.) с вероятностью 0,3.
Построить маленький завод. При этом возможен большой спрос (годовой доход 150 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 25 тыс. долл.) с вероятностью 0,3.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,8 и 0,2 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,9 и 0,1 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 2
 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
В офисе 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с 6 другими? Может ли в офисе, в котором каждый телефон соединен ровно с 5 другими, быть ровно 17 телефонов?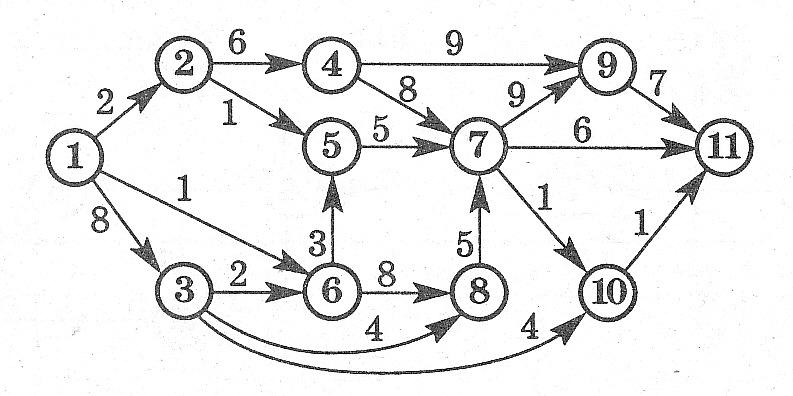
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена?
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 245 тыс. долл.) с вероятностью 0,65 и низкий спрос (ежегодные убытки 45 тыс. долл.) с вероятностью 0,35.
Построить маленький завод. При этом возможен большой спрос (годовой доход 145 тыс. долл.) с вероятностью 0,65 и низкий спрос (ежегодные убытки 20 тыс. долл.) с вероятностью 0,35.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,75 и 0,25 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,91 и 0,09 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Основы теории графов.
Вариант 3
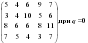 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 0, то это выигрыш 1 игрока, если меньше 0, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 0, то это выигрыш 1 игрока, если меньше 0, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
В группе 30 студентов. Можно ли распределить их так, чтобы каждый имел ровно 5 друзей? Может ли в группе, в которой у каждого студента ровно по 6 друзей, быть ровно 29 человек? 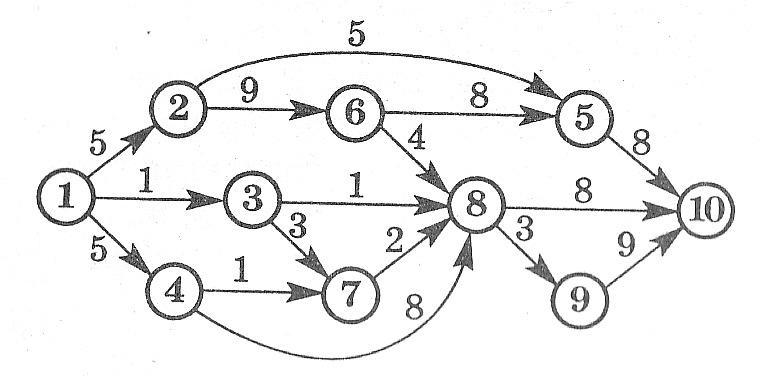
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена?
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 240 тыс. долл.) с вероятностью 0,75 и низкий спрос (ежегодные убытки 40 тыс. долл.) с вероятностью 0,25.
Построить маленький завод. При этом возможен большой спрос (годовой доход 140 тыс. долл.) с вероятностью 0,75 и низкий спрос (ежегодные убытки 15 тыс. долл.) с вероятностью 0,25.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,85 и 0,15 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,92 и 0,08 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Основы теории графов.
Вариант 4
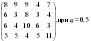 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел – простое число, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел – простое число, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
В группе 30 студентов. Можно ли распределить их так, чтобы каждый имел ровно 6 друзей? Может ли в группе, в которой у каждого студента ровно по 7 друзей, быть ровно 29 человек?
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена? 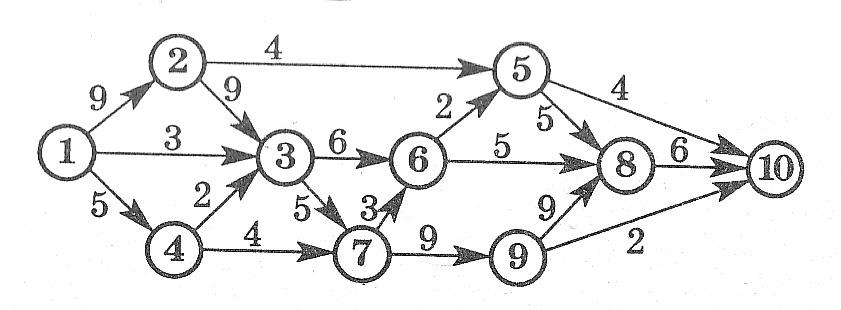
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 235 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 35 тыс. долл.) с вероятностью 0,3.
Построить маленький завод. При этом возможен большой спрос (годовой доход 135 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 10 тыс. долл.) с вероятностью 0,3.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,85 и 0,15 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,93 и 0,07 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 5
 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел кратна трём, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел кратна трём, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Утверждают, что в одной компании из восьми человек каждый знаком только с тремя другими. Возможна ли такая компания? Изобразить графы, которые могут соответствовать такой компании.
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена? 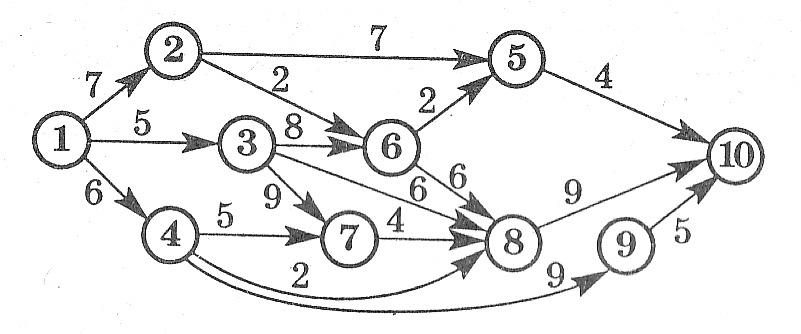
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 230 тыс. долл.) с вероятностью 0,65 и низкий спрос (ежегодные убытки 30 тыс. долл.) с вероятностью 0,35.
Построить маленький завод. При этом возможен большой спрос (годовой доход 130 тыс. долл.) с вероятностью 0,65 и низкий спрос (ежегодные убытки 5 тыс. долл.) с вероятностью 0,35.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,8 и 0,2 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,94 и 0,06 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 6
 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 6, то это выигрыш 1 игрока, если меньше 6, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 6, то это выигрыш 1 игрока, если меньше 6, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Может ли так случиться, что в одной компании из шести человек каждый знаком только с двумя другими? Изобразить графы, которые могут соответствовать такой компании.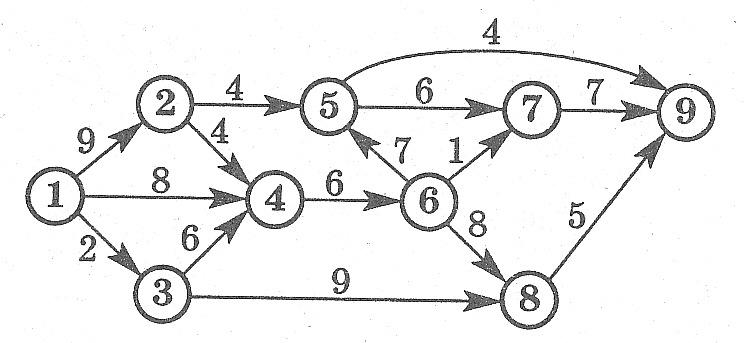
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена?
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 255 тыс. долл.) с вероятностью 0,75 и низкий спрос (ежегодные убытки 55 тыс. долл.) с вероятностью 0,25.
Построить маленький завод. При этом возможен большой спрос (годовой доход 155 тыс. долл.) с вероятностью 0,75 и низкий спрос (ежегодные убытки 30 тыс. долл.) с вероятностью 0,25.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,75 и 0,25 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,95 и 0,05 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 7
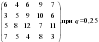 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 3, то это выигрыш 1 игрока, если меньше 3, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 3, то это выигрыш 1 игрока, если меньше 3, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Утверждают, что в одной компании из пяти человек каждый знаком только с тремя другими. Возможна ли такая компания? Показать ситуацию с помощью графа.
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена? 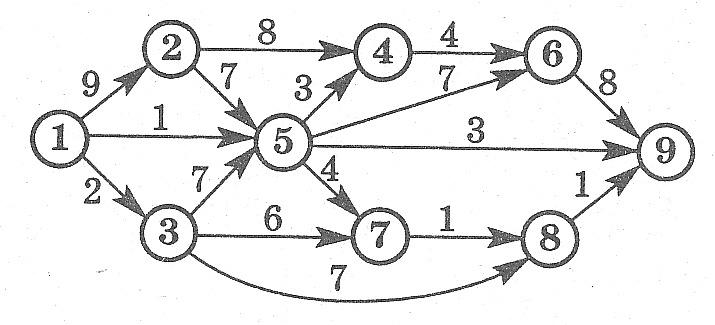
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 260 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 60 тыс. долл.) с вероятностью 0,3.
Построить маленький завод. При этом возможен большой спрос (годовой доход 160 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 35 тыс. долл.) с вероятностью 0,3.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,75 и 0,25 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,94 и 0,06 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 8
Два игрока по очереди бросают игральный кубик. Если произведение выпавших чисел четное, то это выигрыш 1 игрока, если нечетное, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
 Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Может ли так случиться, что в одной компании из семи человек каждый знаком только с двумя другими? Показать ситуацию с помощью графа.
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена? 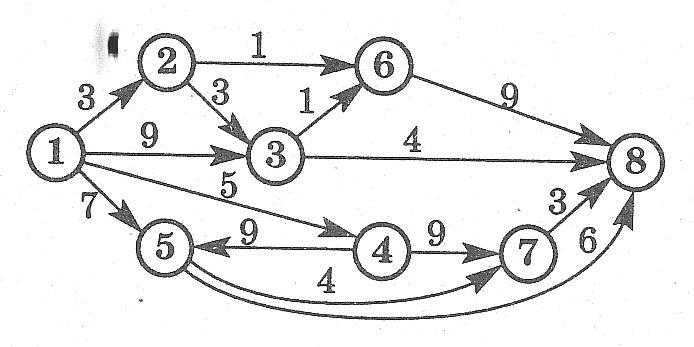
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 265 тыс. долл.) с вероятностью 0,65 и низкий спрос (ежегодные убытки 65 тыс. долл.) с вероятностью 0,35.
Построить маленький завод. При этом возможен большой спрос (годовой доход 165 тыс. долл.) с вероятностью 0,65 и низкий спрос (ежегодные убытки 40 тыс. долл.) с вероятностью 0,35.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,85 и 0,15 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,93 и 0,07 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 9
 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 2, то это выигрыш 1 игрока, если меньше 2, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 2, то это выигрыш 1 игрока, если меньше 2, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Девятнадцать ученых, участвовавших в научной конференции, обменялись рукопожатиями. Сколько всего было сделано рукопожатий? На прощание ученые обменялись визитными карточками. Сколько карточек было передано из рук в руки?
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена? 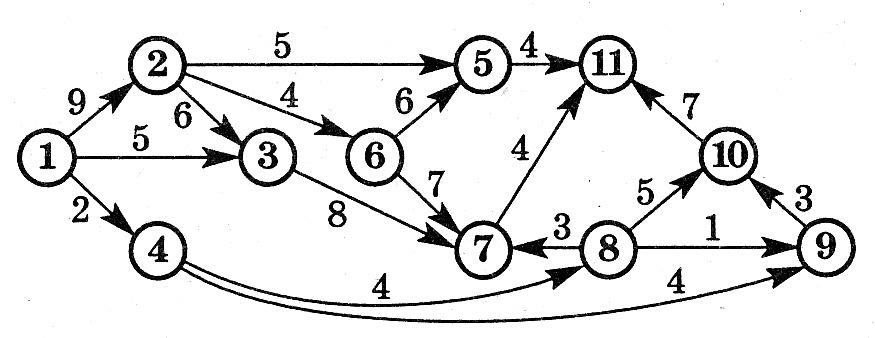
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 270 тыс. долл.) с вероятностью 0,75 и низкий спрос (ежегодные убытки 70 тыс. долл.) с вероятностью 0,25.
Построить маленький завод. При этом возможен большой спрос (годовой доход 170 тыс. долл.) с вероятностью 0,75 и низкий спрос (ежегодные убытки 45 тыс. долл.) с вероятностью 0,25.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,8 и 0,2 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,92 и 0,08 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?
Контрольная работа по темам:
Элементы теории игр. Элементы теории графов.
Вариант 10
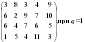 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 5, то это выигрыш 1 игрока, если меньше 5, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 5, то это выигрыш 1 игрока, если меньше 5, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Девять студентов одной группы сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно? Сколько студентов другой группы играли в шахматы, если между ними была сыграна 21 партия? 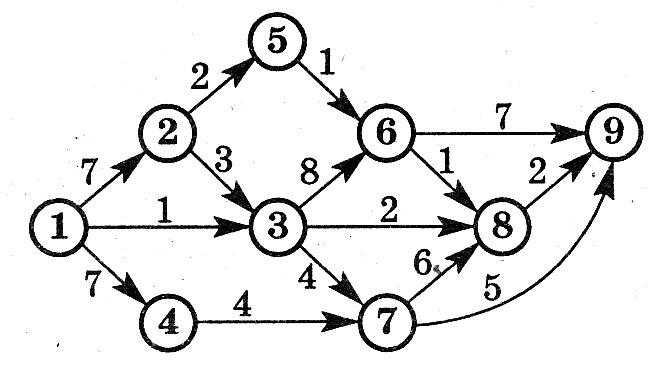
Какое максимальное количество грузов из первого пункта в последний может послать транспортная компания, если пропускная способность путей между пунктами транспортной сети ограничена?
Компания рассматривает вопрос о строительстве нового завода. Возможны 3 варианта действий:
Построить большой завод. При этом возможен большой спрос (годовой доход 275 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 75 тыс. долл.) с вероятностью 0,3.
Построить маленький завод. При этом возможен большой спрос (годовой доход 175 тыс. долл.) с вероятностью 0,7 и низкий спрос (ежегодные убытки 50 тыс. долл.) с вероятностью 0,3.
Отложить строительство для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностями 0,75 и 0,25 соответственно. В случае позитивной информации вероятности большого и низкого спроса меняются на 0,91 и 0,09 соответственно. Доходы остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовать дерево решений. Какова ожидаемая стоимостная оценка наилучшего решения?







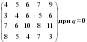 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел четная, то это выигрыш 1 игрока, если нечетная, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
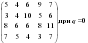 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 0, то это выигрыш 1 игрока, если меньше 0, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 0, то это выигрыш 1 игрока, если меньше 0, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
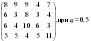 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел – простое число, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел – простое число, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел кратна трём, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел кратна трём, то это выигрыш 1 игрока, если нет, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 6, то это выигрыш 1 игрока, если меньше 6, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 6, то это выигрыш 1 игрока, если меньше 6, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
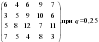 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 3, то это выигрыш 1 игрока, если меньше 3, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 3, то это выигрыш 1 игрока, если меньше 3, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
 Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей
Определить оптимальное решение игры по критериям Вальда, Сэвиджа и Гурвица для игры, заданной матрицей 
 Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 2, то это выигрыш 1 игрока, если меньше 2, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если разность выпавших чисел больше 2, то это выигрыш 1 игрока, если меньше 2, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
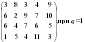 Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 5, то это выигрыш 1 игрока, если меньше 5, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.
Два игрока по очереди бросают игральный кубик. Если сумма выпавших чисел больше 5, то это выигрыш 1 игрока, если меньше 5, то проигрыш. Составить платежную матрицу и найти решение игры, если существует седловая точка.






















