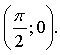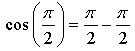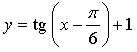Контрольная работа № 3
Вариант 1
1. Не выполняя построения, установите, принадлежит ли графику функции 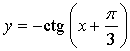 точка:
точка:

2. Исследуйте функцию на четность.
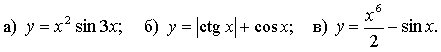
3. Исследуйте функцию 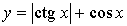 на периодичность; укажите основной период, если он существует.
на периодичность; укажите основной период, если он существует.
4. Решите графически уравнение 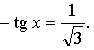
5. Постройте график функции, указанной в пункте а) или б).
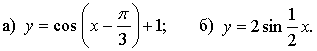
6. При каком значении параметра а неравенство 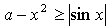 имеет единственное решение? Найдите это решение.
имеет единственное решение? Найдите это решение.
Вариант 2
1. Не выполняя построения, установите, принадлежит ли графику функции 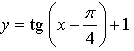 точка:
точка:

2. Исследуйте функцию на четность.
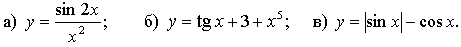
3. Исследуйте функцию 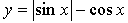 на периодичность; укажите основной период, если он существует.
на периодичность; укажите основной период, если он существует.
4. Решите графически уравнение 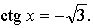
5. Постройте график функции, указанной в пункте а) или б).
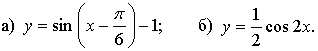
6. При каком значении параметра а неравенство 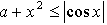 имеет единственное решение? Найдите это решение.
имеет единственное решение? Найдите это решение.
Вариант 3
1. Не выполняя построения, установите, принадлежит ли графику функции 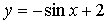 точка:
точка:

2. Исследуйте функцию на четность.
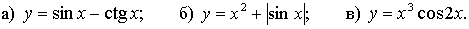
3. Исследуйте функцию 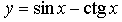 на периодичность; укажите основной период, если он существует.
на периодичность; укажите основной период, если он существует.
4. Решите графически уравнение 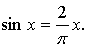
5. Постройте график функции, указанной в пункте а) или б).
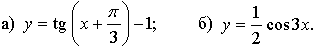
6. При каком значении параметра а неравенство 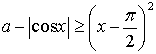 имеет единственное решение? Найдите это решение.
имеет единственное решение? Найдите это решение.
Вариант 4
1. Не выполняя построения, установите, принадлежит ли графику функции 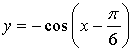 точка:
точка:

2. Исследуйте функцию на четность.
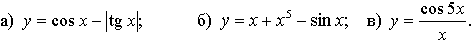
3. Исследуйте функцию 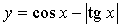 на периодичность; укажите основной период, если он существует.
на периодичность; укажите основной период, если он существует.
4. Решите графически уравнение 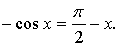
5. Постройте график функции, указанной в пункте а) или б).
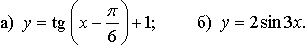
6. При каком значении параметра а неравенство 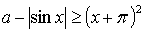 имеет единственное решение? Найдите это решение.
имеет единственное решение? Найдите это решение.
Рекомендации по оцениванию контрольной работы
За успешное выполнение только заданий обязательного минимума (до первой черты) – оценка «3»; за успешное выполнение заданий обязательного уровня и одного дополнительного (после первой черты) – оценка «4»; за успешное выполнение заданий всех трех уровней – оценка «5». При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Решение контрольной работы
Вариант 1
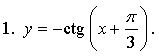
а) 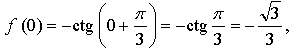 значит, точка
значит, точка 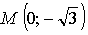 не принадлежит графику функции.
не принадлежит графику функции.
б) 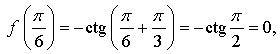 значит, точка
значит, точка 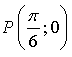 принадлежит графику функции.
принадлежит графику функции.
Ответ: а) нет; б) да.
2. а) 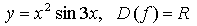
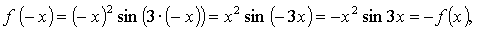 значит, функция нечетная.
значит, функция нечетная.
б) 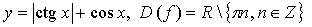
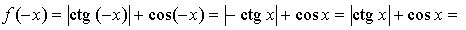 f(x), значит, функция четная.
f(x), значит, функция четная.
в) 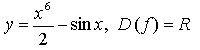
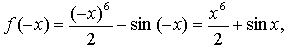 значит, функция ни четная, ни нечетная.
значит, функция ни четная, ни нечетная.
Ответ: а) нечетная; б) четная; в) ни четная, ни нечетная.
3. 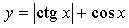
Пусть Т – основной период функции, тогда
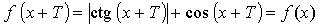
Т = П – основной период для функции 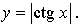
Т = 2П – основной период для функции у = cos х.
Значит, 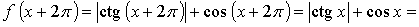 f(x).
f(x).
Ответ: Т = 2П.
4. 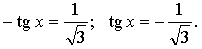
Построим графики функций y = tg x и 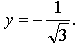
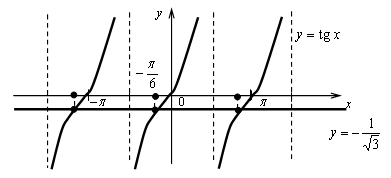
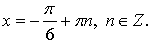
Ответ: 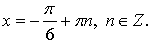
5. а) 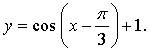
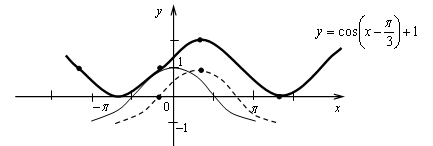
График функции получен параллельным переносом графика функции у = cos х на 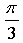 единиц вправо и на 1 единицу вверх.
единиц вправо и на 1 единицу вверх.
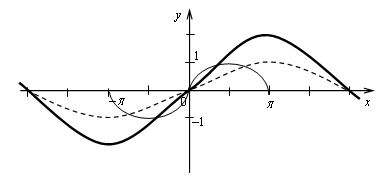
б) 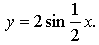
График функции получен из графика функции у = sin х растяжением от оси х и от оси у в 2 раза.
6. 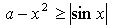
у = а – х2
у = sin х
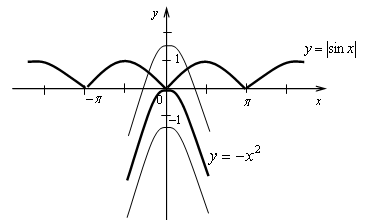
Если а
а 0, то неравенство имеет бесконечно много решений;
а = 0, то неравенство имеет единственное решение х = 0.
Ответ: а = 0.
Вариант 2
1. 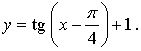
а) 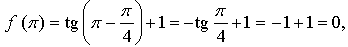 значит, точка
значит, точка 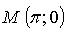 принадлежит графику функции.
принадлежит графику функции.
б) 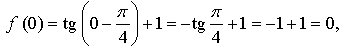 значит, точка
значит, точка 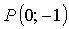 не принадлежит графику функции.
не принадлежит графику функции.
Ответ: а) да; б) нет.
2. а) 
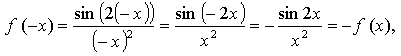 значит, функция нечетная.
значит, функция нечетная.
б) 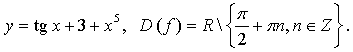
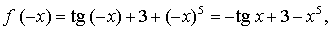 значит, функция ни четная, ни нечетная.
значит, функция ни четная, ни нечетная.
в) 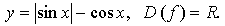
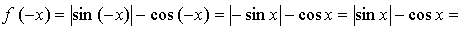 f(x), значит, функция четная.
f(x), значит, функция четная.
Ответ: а) нечетная, б) ни четная, ни нечетная; в) четная.
3. 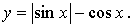
Пусть Т – основной период функции, тогда
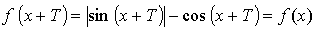
Т = П – основной период для функции у = sin х.
Т = 2П – основной период для функции у = cos х.
Значит, 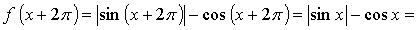 f(x).
f(x).
Ответ: Т = 2П.
4. 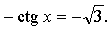
Построим графики функций y = ctg x и 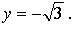
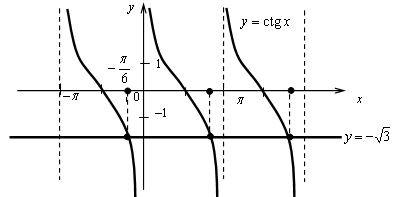
Ответ: 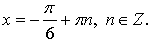
5. а) 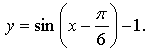
График функции получен параллельным переносом графика функции у = sin х на 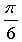 единиц вправо и на 1 единицу вниз.
единиц вправо и на 1 единицу вниз.
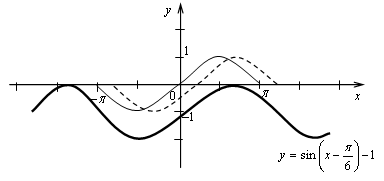
б) 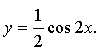
График получен сжатием графика функции у = cos 2х к оси х и к оси у в 2 раза.

6. 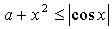
у = а + х2
у = cos х
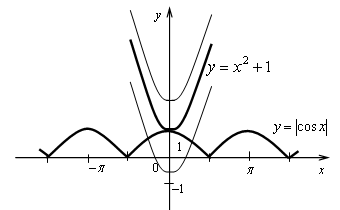
Если а 1, то неравенство не имеет решений;
а
а = 1, то неравенство имеет единственное решение х = 0.
Ответ: а = 1.
Вариант 3
1. у = –sin х + 2.
а) 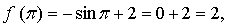 значит, точка
значит, точка 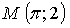 принадлежит графику функции.
принадлежит графику функции.
б) 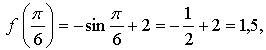 значит, точка
значит, точка 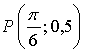 не принадлежит графику функции.
не принадлежит графику функции.
Ответ: а) да; б) нет.
2. а) 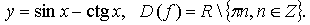
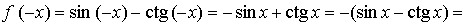 –f(x), значит, функция нечетная.
–f(x), значит, функция нечетная.
б) 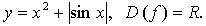
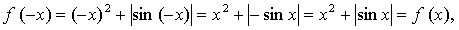 значит, функция четная.
значит, функция четная.
в) 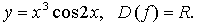
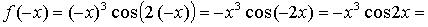 –f(x), значит, функция нечетная.
–f(x), значит, функция нечетная.
Ответ: а) нечетная; б) четная; в) нечетная.
3. 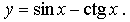
Пусть Т – основной период функции, тогда
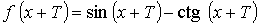
Т = 2П – основной период для функции у = sin х.
Т = П – основной период для функции y = ctg x.
Значит, 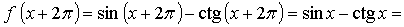 f(x).
f(x).
Ответ: Т = 2П.
4. 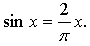
Построим графики функций у = sin х и 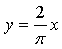 – прямая, проходящая через точки (0; 0) и (; 2).
– прямая, проходящая через точки (0; 0) и (; 2).
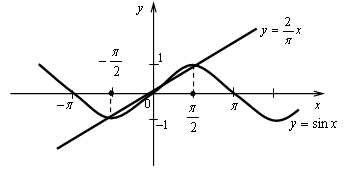
Проверим полученные решения:

1 = 1 – верно. –1 = –1 – верно.
Ответ: 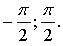
5. а) 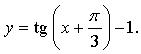
График функции получен параллельным переносом графика функции y = tg x на 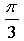 единицы влево и на 1 единицу вниз.
единицы влево и на 1 единицу вниз.
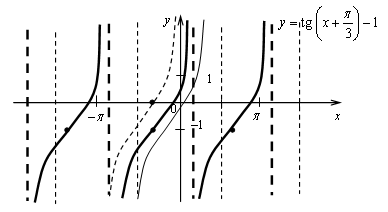
б) 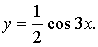
График функции получен сжатием графика функции у = cos х в 2 раза к оси х и в 3 раза к оси у.
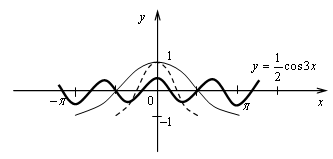
6. 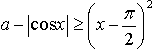
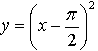 – график получен параллельным переносом графика функции у = х2 на
– график получен параллельным переносом графика функции у = х2 на 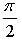 единиц вправо.
единиц вправо.
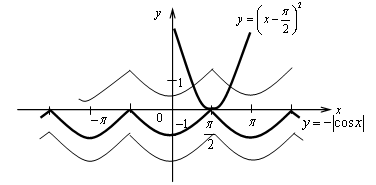
Если а 0, то неравенство имеет бесконечно много решений;
а
а = 0, то неравенство имеет единственное решение 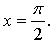
Ответ: а = 0.
Вариант 4
1. 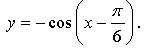
а) 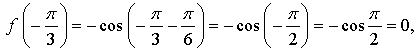 значит, точка
значит, точка 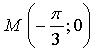 принадлежит графику функции.
принадлежит графику функции.
б) 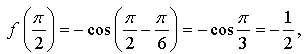 значит, точка
значит, точка 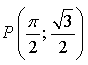 не принадлежит графику функции.
не принадлежит графику функции.
Ответ: а) да; б) нет.
2. а) 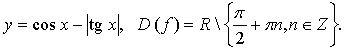
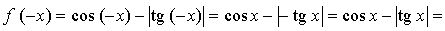 f(x), значит, функция четная.
f(x), значит, функция четная.
б) 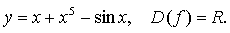
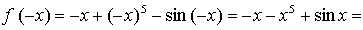
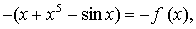 значит, функция нечетная.
значит, функция нечетная.
в) 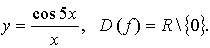
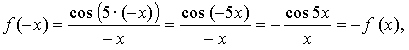 значит, функция нечетная.
значит, функция нечетная.
Ответ: а) четная, б) нечетная; в) нечетная.
3. 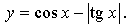
Пусть Т – основной период функции, тогда
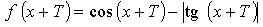
Т = 2П – основной период для функции у = cos х.
Т = П – основной период для функции y = tg x.
Значит, 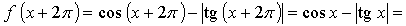 f(x).
f(x).
Ответ: Т = 2П.
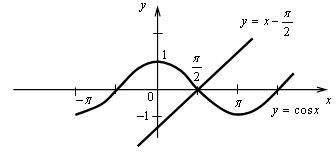
4. 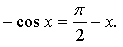
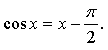
Построим графики функций у = cos х и 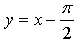 – прямая, проходящая через точки
– прямая, проходящая через точки 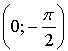 и
и 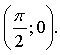
Проверим полученное решение: 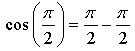
0 = 0 – верно.
Ответ: 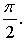
5. а) 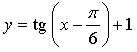
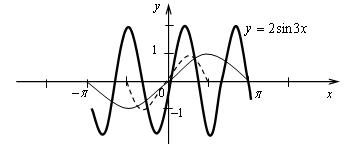
График функции получен параллельным переносом графика функции y = tg x на 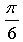 единиц вправо и на 1 единицу вверх.
единиц вправо и на 1 единицу вверх.
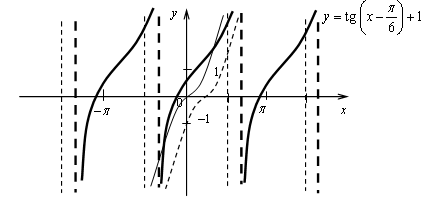
б) у = 2sin 3х.
График функции получен сжатием графика функции у = sin х к оси у в 3 раза и растяжением от оси х в 2 раза.
6. 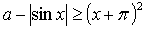
у = (х + )2 – график получен параллельным переносом графика функции у = х2 на единиц влево.
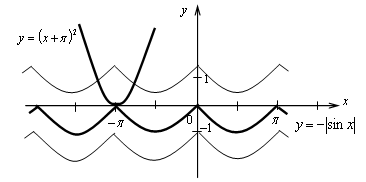
Если а 0, то неравенство имеет бесконечно много решений;
а
а = 0, то неравенство имеет единственное решение х = –.
Ответ: а = 0.





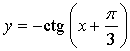 точка:
точка:
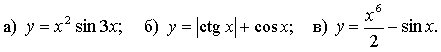
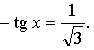
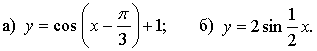
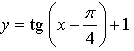 точка:
точка: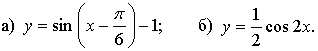

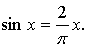
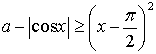 имеет единственное решение? Найдите это решение.
имеет единственное решение? Найдите это решение.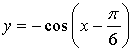 точка:
точка:
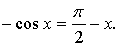
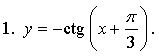
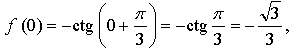 значит, точка
значит, точка 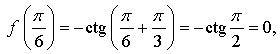 значит, точка
значит, точка 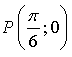 принадлежит графику функции.
принадлежит графику функции.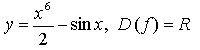

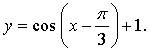



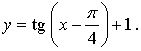
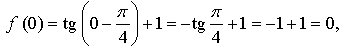 значит, точка
значит, точка 
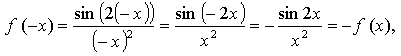 значит, функция нечетная.
значит, функция нечетная.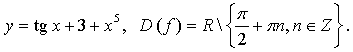

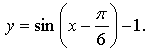

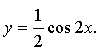


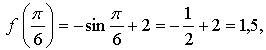 значит, точка
значит, точка 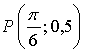 не принадлежит графику функции.
не принадлежит графику функции.

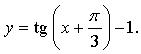


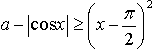
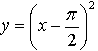 – график получен параллельным переносом графика функции у = х2 на
– график получен параллельным переносом графика функции у = х2 на 
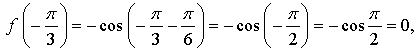 значит, точка
значит, точка 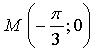 принадлежит графику функции.
принадлежит графику функции.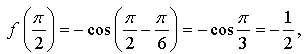 значит, точка
значит, точка 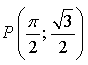 не принадлежит графику функции.
не принадлежит графику функции.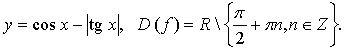
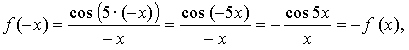 значит, функция нечетная.
значит, функция нечетная.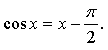
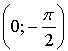 и
и